基于改进多元多尺度熵的人体步态加速度信号分类*

2015-08-24王旭尧徐永红

传感技术学报 2015年12期

关键词：粒化步态复杂度

王旭尧，徐永红

（燕山大学生物医学工程研究所，河北秦皇岛066004）

基于改进多元多尺度熵的人体步态加速度信号分类*

王旭尧，徐永红*

（燕山大学生物医学工程研究所，河北秦皇岛066004）

传统多元多尺度熵算法在处理有限长时间序列时，会使均值曲线产生较大的波动，并且阈值的选取也会对结果产生较大的影响。因此，在传统多元多尺度熵的基础上首先对传统粗粒化方式进行了改进，改进后的算法采用滑动均值滤波使粗粒化后各尺度上的时间序列与原始时间序列长度一致，减小了所计算多元多尺度熵的离散性。此外，本文算法在保持多元样本熵硬阈值优点的同时，通过定义模糊隶属度函数来统计两复合延迟矢量距离略大于阈值的情况，既降低了传统方法对阈值的依赖性，也很好的解决了传统阈值所导致的不稳定现象。最后用仿真数据对该算法进行了验证，并将其应用于不同人体步态加速度信号的复杂度评价和分类，结果表明改进算法的识别效果明显优于传统多元多尺度熵。

步态分类；加速度信号；改进多元多尺度熵；传统多元多尺度熵

EEACC：7230doi：10.3969/j.issn.1004-1699.2015.12.013

人体生理信号蕴含着大量能够反映人体健康状况、精神状态的有用信息。目前，人体生理信号的分析、处理已成为临床医学、康复医疗的一个重要研究领域。步态作为人体生理信号中具有特异性的一种指人在行走时的姿态，是由人体上百种骨骼、肌肉共同作用的结果［1］。就不同的个体而言，由于存在性别、身高、体重等差异，因此其步态也不尽相同。而对于同一个人来说，其年龄变化、身体健康程度、精神状态的改变，对步态也会有不同程度的影响［2］。加速度作为人体步态动力学中的重要参数，包含了大量人体步态中有价值的信息。因此，研究人体步态加速度数据，对人体的行为进行识别，可为病人的监护［3］、运动员辅助训练［4］提供有力的工具。

目前，大多数人体行为识别的方法都是针对于图像的，而在人体运动环境下拍摄的图像要受到光照、分辨率、影子等多方便因素的影响，会给基于图像的行为检测和表征带来很大的困难［5］。采用人体步态加速度数据对人体行为进行识别的方法具有受环境影响小、不受距离限制等优点。起初，Heikki Ailisto［6］等提出一种利用加速度传感器来采集人体步态数据的新方法，该方法降低了数据处理难度，避免了动态情况下多种因素对捕捉图像的不利影响，为步态特征的获取开辟了一条新途径。随着惯性技术（MEMS）的迅猛发展，利用人体步态加速度对人体行为进行识别逐渐成为许多专家和学者关注的热点。刘晓婷［7］等人运用加速度传感器采集了几种人体日常生活步行姿态，并利用将小波变换与多尺度熵结合对健康人群不同行为的加速度信号进行特征值提取，为进一步研究人体加速度信息和行为信息提出了一种可行的有效的分析方法。Maquire D［8］等人通过固定于大腿处的三轴加速度传感器实时采集人体不同行为下的加速度数据，用窗函数法提取出加速度数据中的平均值，标准偏差作为特征送入到KNN分类器中进行分类，最终获得了90.07%的识别率。He Zhenyu［9］通过对人体不同行为加速度数据的研究，提出一种基于AR模型的特征提取方法，用该方法从加速度数据提取出的平均值、标准偏差送入到SVM分类器中进行分类，最终识别率达到了92.25%。徐川龙［10］等提出了一种基于单个三轴加速度计的人体行为及特征提取方法，该方法通过提取人体正常行走、上楼、下楼的步态的多种统计特征，并将提取后的特征送入到SVM分类器中进行分类，获得了95%的识别率。以上三种方法只利用某种特定的分类器对人体行为加速度数据进行分类，对于其他分类器的分类效果并未做深入研究。

近年来，在多元多尺度样本熵的相关研究中，文献［11］将其应用于心电信号，有效的揭示了多通道心电信号的长时相关性。由于该算法计算复杂度较高，数据量较大，会造成系统内存溢出。崔杰［12］等对多元多尺度样本熵算法进行了改进，并成功将该算法应用到癫痫脑电信号的分类当中。但此方法的结果很大程度上依赖于小波基的选取，且统计稳定性较差。人体步态信号、心电信号和癫痫脑电信号同属人体生理信号中的低频信号，与生理系统本身的自组织性密切相关。生理系统的自组织性使人体步态信号表现出自相似和长时相关性，这一点与癫痫脑电信号、心电信号相同。因此，本文在文献［12］的基础上进行了改进，提出改进多元多尺度熵算法，并将该算法应用于上、下楼步态和正常步态的复杂度区分领域。实验提取三种状态下的三轴加速度数据代表三通道的原始加速度时间序列，分别利用改进多元多尺度熵和传统多元多尺度熵算法求出各时间序列在不同尺度下的均值和方差，对其分析和对比。选取两种算法复杂度区分较好的尺度为特征送入到不同的分类器中进行分类，并对分类结果进行了比较。

1　算法描述

1.1改进多元多尺度熵

改进多元多尺度熵由改进粗粒化和改进样本熵两部分组成。

1.1.1改进粗粒化

为了引出改进粗粒化算法，这里首先介绍一下传统粗粒化方法。定义p个变量的时间序列，在各尺度上对原始时间序列进行粗粒化，粗粒化后的时间序列为：

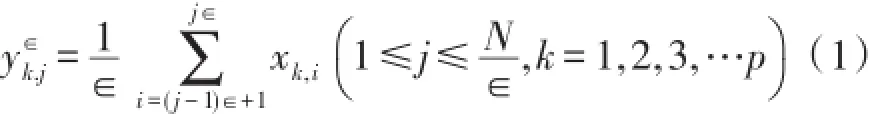
以尺度3为例，传统粗粒化过程如图1所示。

图1　R传统粗粒化过程

从图1可以看出，传统粗粒化是将原始时间序列按尺度因子依次进行压缩，当原始时间序列数据长度为有限长时，随着尺度的增加，粗粒化后的时间序列长度不断减小，并且当原始数据长度不是尺度因子的整数倍时，将会造成部分数据的丢失。以上因素必然会影响多元多尺度熵算法的计算精度。针对上述缺点，本文提出改进粗粒化算法，在各尺度上采用滑动平均的方法对原始时间序列进行粗粒化，既保证了各尺度上粗粒化后的时间序列与原始时间序列长度一致，同时也避免了数据丢失的产生，大大提高了后续算法的准确性。具体过程如图2所示。

图2　R改进粗粒化过程

1.1.2改进样本熵

改进样本熵算法具体可分为如下几个步骤：

①定义物理模糊隶属度函数为：令域X表示一个距离集合，对∀x∈X且x≥0，∃K（x）∈［0,1］，称K（x）为域X上的隶属度函数，即：

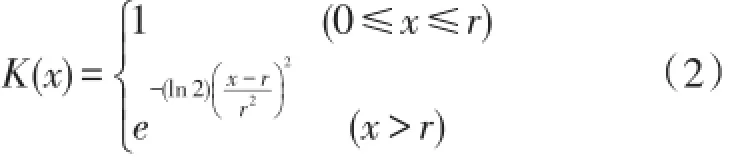
②求其中任意两个复合延迟矢量的契比雪夫距离，即：

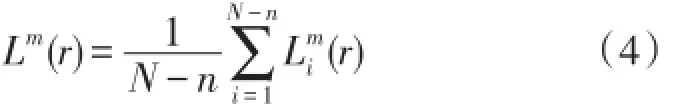
④将复合延迟矢量Ym（i）中的所有向量都嵌入m+1维［10］，得到N-n个复合延迟矢量Ym+1（i）。针对Ym+1（i）重复上述步骤，得到嵌入维度为m+1时的条件概率Lm+1（r）：

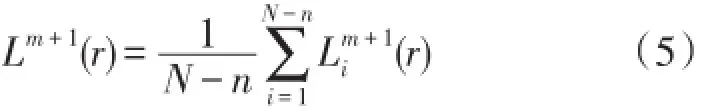
⑤计算两条件概率的比值的负自然对数，即求得多元多尺度模糊熵的值：

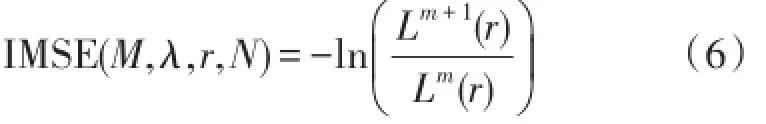
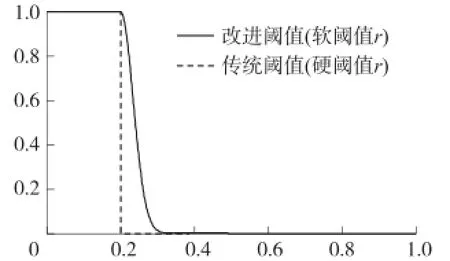
图3　R传统阈值（硬阈值）与改进阈值（软阈值）对比

2　算法验证与分析

2.1仿真实验分析

由文献［13］可知，对于不相关的白噪声而言，复杂度随尺度的增加而降低，而对于远程相关的1/f噪声来说，其复杂度随着尺度的增加有缓慢下降的趋势；在各尺度上，1/f噪声的复杂度皆大于白噪声的复杂度。基于上述结论，本文分别选取500、1 000、1 500个采样点的随机白噪声和1/f噪声对传统粗粒化多元样本熵和改进粗粒化多元样本熵进行对比，其中多元样本熵所用参数为：尺度因子∈= 1～20，嵌入维度M=2，延迟矢量tau=1，相似容限r= 0.2×std（std表示归一化时间序列的标准偏差）。从图4中可以看出，随机白噪声随着尺度的增加，复杂度逐渐降低，而1/f噪声具有远程相关性，随着尺度的增加，其复杂度缓慢下降逐渐趋于平稳，各尺度上1/f噪声复杂度均大于随机噪声的复杂度，这与文献中的结论相一致。当采样点为500点时观察图a、图b可知：在1/f噪声、随机白噪声复杂度的区分效果上，传统粗粒化后的多元样本熵，在各尺度上由随机误差所引起的均值曲线波动较大，且随着尺度的增加方差越来越大。改进粗粒化后的多元样本熵，各尺度上由随机误差所引起的均值曲线波动较小，曲线较为平滑，方差变化较小。对比图c和图e，对于远程相关的1/f噪声来说，当采样点从1 000点增加到1 500点时，传统粗粒化后的数据在各尺度上均值曲线波动逐渐减小，方差也逐渐变小；而改进粗粒化后的数据在各尺度上均值曲线依然平滑、方差变化也不大。当采样点为1 500点时，传统粗粒化与改进粗粒化的效果比较接近。在随机白噪声复杂度的区分上，对比图d和图f，当采样点为1 000点时传统粗粒化与改进粗粒化在各尺度上均值分布相一致，而改进粗粒化方差要小于传统粗粒化方差，当采样点增加到1 500点时，传统粗粒化均值方差曲线与改进粗粒化均值方差曲线趋近于重合。由此可见，当样本的数据长度较短时，采用改进粗粒化算法的效果要明显优于传统粗粒化算法。

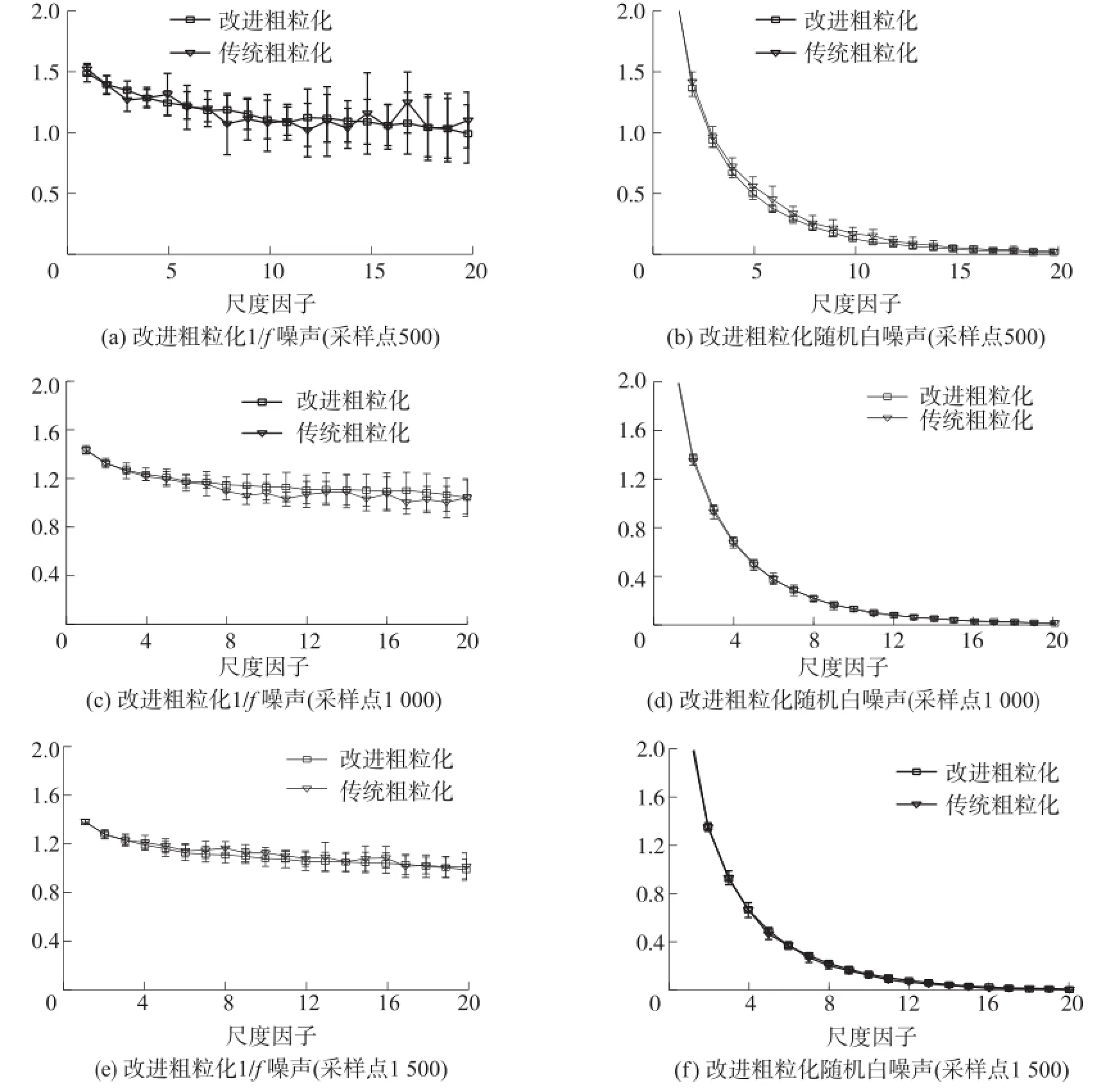
图4　R改进粗粒化与传统粗粒化结果对比

为了进一步证明改进样本熵的优点，实验生成4个三通道的时间序列信号，分别为：3个通道的1/f噪声；两个通道的1/f噪声和1个通道的随机白噪声；1个通道的1/f噪声和另外两个通道的随机白噪声；3个通道都为随机白噪声。其中粗粒化方式都采取传统粗粒化方式，且改进样本熵与传统样本熵所用参数皆为M=2，tau=1，r=0.2×std。传统粗粒化改进样本熵、传统多元多尺度样本熵特征提取结果如图5、图6所示。从图5与图6中都可以看出：随着尺度的增加，4个三通道时间序列复杂度都有下降的趋势，各尺度上，三通道皆为不相关随机白噪声的复杂度最低，随着1/f噪声通道数的增加，复杂度逐渐升高，当三通道皆为1/f噪声时复杂度达到最高。在图5中：各时间序列在采用传统多元多尺度样本熵特征提取后，在尺度1～尺度4上，通道中含有远程相关1/f噪声的方差曲线都有不同程度的交叠，随着尺度的增加，三通道1/f噪声与两通道1/f噪声（另一个通道为随机白噪声）之间的方差曲线仍未完全分开，区分性很差。从图6可以看出：在传统粗粒化改进样本熵特征提取后，所有尺度上方差曲线皆较小，从尺度3开始各通道时间序列的方差曲线均无交叠，随着尺度的的增加，各时间序列复杂度的区分效果越来越明显。因此，在1/f噪声与随机白噪声复杂度的区分效果上，改进样本熵要优于多传统样本熵。

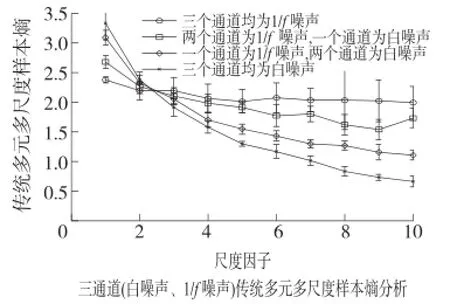
图5　R三通道（白噪声、1/f噪声）传统多元多尺度样本熵分析

图6　R三通道（白噪声、1/f噪声）传统粗粒化改进样本熵分析

2.2人体步态加速度数据的复杂度分析

实验采用国外公开数据库（http：//www.ess. tu-darmstadt.de/datasets）中的人体步态数据。实验对象为5名健康男性，年龄在24岁～31岁之间。实验采集过程为：首先将三轴加速度传感器绑于各实验对象右腿膝盖上部，要求每一个受试者在计算机科学大楼内分别按正常行走、上楼、下楼的顺序进行运动，各受试者在运动的过程中，传感器以250 Hz的采样频率实时采集实验对象在当前状态下的步态加速度数据，最终传感器采集到的数据被记录于戴在受试者臀部的微处理器内。其中，各实验对象的每种运动状态重复采集5次，每次持续时间为25 min。为了消除偶然性，一周之后，要求其中三名实验对象重复上述实验，并将实验结果记录下来。分别选取上正常行走、上楼、下楼步态中前4 000个采样点的Z轴加速度数据，其波形如图7所示。

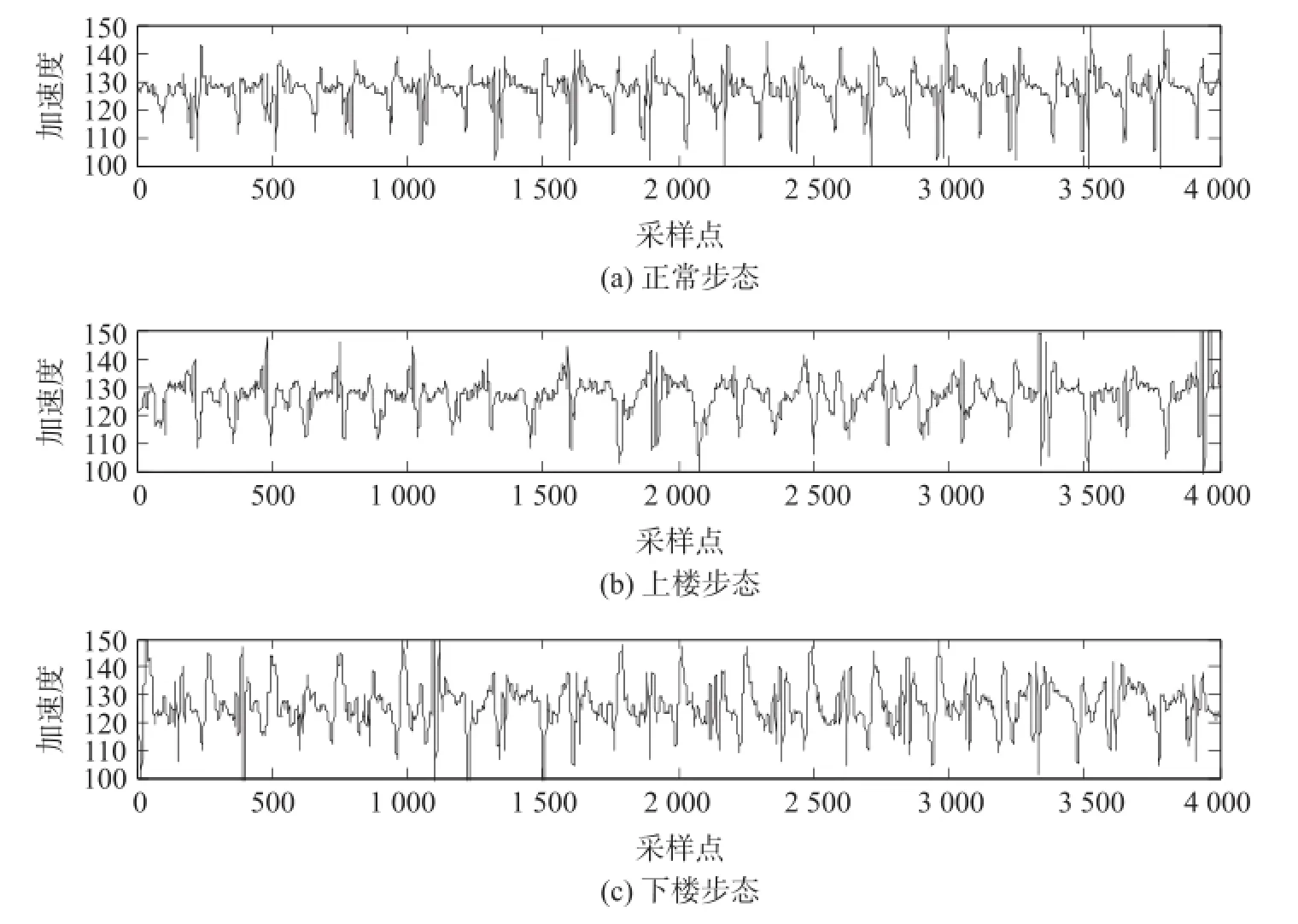
图7　R正常步态、上楼、下楼步态的原始加速度波形曲线

从图7中可以看出：各采样点处，正常步态、上楼、下楼步态皆呈现出明显的周期性；对比三种状态下的加速度曲线可以发现，正常步态和上楼步态的加速度曲线波动较小，幅值较为接近；而下楼步态的加速度曲线波动幅度较大，其幅值范围也比正常步态和上楼步态的范围要宽。

实验首先提取数据库中正常步态、上楼步态和下楼步态的三轴加速度数据，分别代表三个通道的原始步态加速度时间序列。为了简化运算，实验对三通道加速度数据依次进行了归一化处理，保证各通道数据的幅值在0～1范围内。归一化后的三通道加速度时间序列按尺度因子进行粗粒化，粗粒化采用滑动窗口的方式，使各尺度上数据的长度为原始时间序列（ω为尺度因子）。粗粒化后的时间序列用传统多元样本熵进行特征提取，其中多元样本熵所选参数为：尺度因子ω=1～10，嵌入维度m=2，延迟矢量tau=1，相似容限r=0.2×std（std表示归一化时间序列的标准差）。传统多元多尺度熵特征提取结果如图8所示。

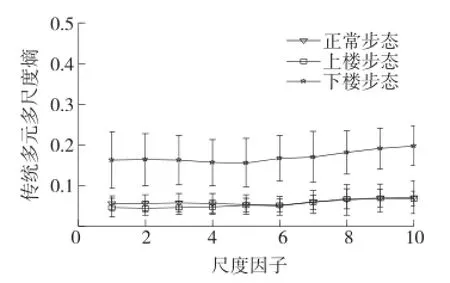
图8　R传统多元多尺度熵特征提取图

由图8可以看出：各尺度上正常步态、上楼步态、下楼步态的均值曲线波动较大，从尺度1开始下楼步态和其余两数据集的均值相距较远，方差曲线无交叉重叠，且随着尺度的增加区分程度有逐渐增加的趋势。从总体上看，下楼步态的复杂度大于正常步态、上楼步态的复杂度；而在对正常步态和上楼步态的复杂度区分方面，两数据集在低尺度上均值相距很近，方差曲线有不同程度的交叠；随着尺度的增加两数据集均值逐渐发生重合，同时其方差曲线的交叠部分也逐渐增大，在尺度5～尺度10之间，两数据集的均值、方差曲线已完全交叠，无法对两数据集的复杂度进行区分。

为了证明本文算法的优点，实验运用改进多元多尺度熵对三种状态下步态加速度信号的复杂度进行了区分，将三通道中的原始加速度时间序列进行归一化处理后，用改进粗粒化算法对归一化后的三通道步态加速度时间序列进行粗粒化，该算法采用滑动均值滤波的方法使各尺度上粗粒化后的时间序列与原始步态时间序列长度保持一致。并利用改进样本熵对粗粒化后的时间序列进行特征提取。其中，改进多元多尺度熵所用参数与传统多元多尺度熵所用参数一致。改进多元多尺度熵特征提取效果如图9所示。

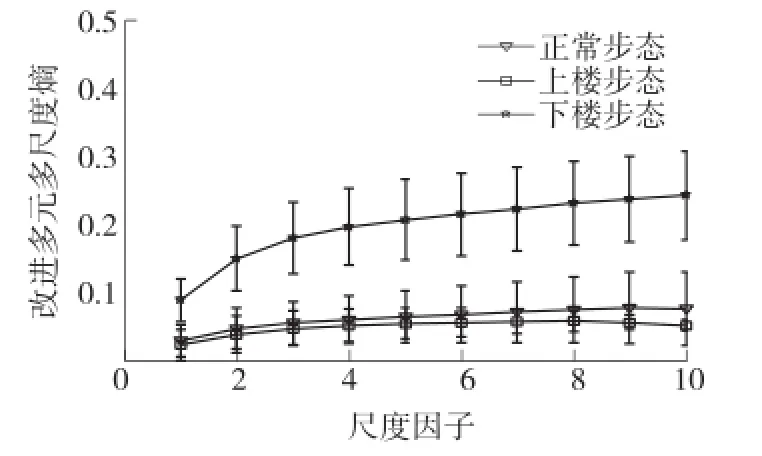
图9　R改进多元多尺度熵特征提取图

从图9中可以发现：用本文算法对三数据集进行特征提取后，各尺度上各数据集均值波动较小，曲线更加平滑；从尺度1开始，下楼步态与其余两数据集的均值相距较远，方差曲线无交叉重叠，且随着尺度的增加区分程度越来越大。而在对正常步态和上楼步态的复杂度区分方面，在低尺度上，两数据集的均值和方差曲线虽完全交叠，但随着尺度的增加，两数据集均值相距逐渐增大，方差曲线交叠程度明显减小。从整体上能够看出，随着尺度的增大，上楼步态的复杂度明显增大；正常步态的复杂度缓慢增大，逐渐趋于平稳；而上楼步态的复杂度有缓慢下降的趋势。因此可以得出：下楼步态的复杂程度最高，正常步态的复杂度次之，上楼步态的复杂度最低。由此可知，改进多元多尺度熵特的征提取结果要优于传统多元多尺度熵。

选取尺度9和尺度10为特征，两数据集特征提取后的散点图如图10所示：从图10中可以看出，下楼步态与其余两类数据分布较远，区分性非常显著；上楼步态与正常步态虽有部分交叠，但正常步态的复杂度主要分布在图的中间位置，而上楼步态的复杂度集中在图的下方，因此可以判定，下楼步态的复杂度高于正常步态的复杂度，而上楼步态的复杂度最低。

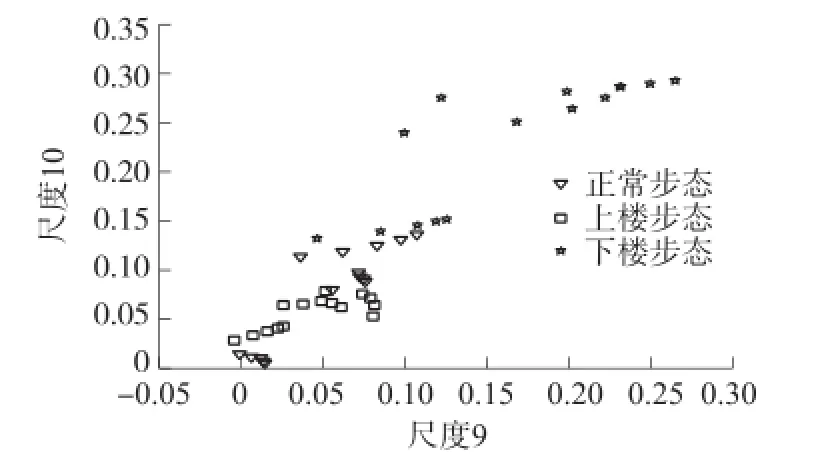
图10　R三数据集在尺度9、尺度10上的改进多元多尺度熵散点图

在实验环境为Ineter（R）Pentium（R）CPU，2.0 G主频，2.0 GB内存，Matlab-2012a的前提下，选取两种算法特征提取后区分效果较好的相同尺度为特征，组成相应的特征向量。

将特征向量进行归一化处理，量化后的数据采用留一法分别送入到BP神经网络分类器，概率神经网络（PNN）分类器、线性判别（LDA）分类器及支持向量机（SVM）分类器中进行交叉验证。其中，BP神经网络网络训练所采用的参数为：训练终止目标0.000 000 4，学习率为0.01，最大循环次数1 000次；概率神经网络（PNN）扩展速度为1.5；SVM分类器采用RBF径向基核函数，惩罚因子C= 1；最后将测试集送到训练好的各分类器中进行测试，分类结果如表1所示。

表1　R三数据集在不同分类器上的识别率

由表1可以得知：本文算法的识别率皆高于传统多元多尺度样本熵，且最大识别率达到了96.5%。将本文算法的最高识别率与目前国际上针对人体正常步态、上楼、下楼步态数据的最高分类精度进行对比，本文算法体现出明显的优越性。其中文献［14］首先利用三轴加速度传感器采集到了正常行走、上楼、下楼三种状态下的加速度信号，对采集到的信号进行小波分解，提取能量特征和样本熵特征，并将提取后的特征参数送到贝叶斯分类器和决策树分类器中进行分类识别。具体结果如表2所示。

表2　R不同特征提取和分类方法正确率对比

3　结论

本文在传统多元多尺度熵的基础上进行了改进，提出一种改进多元多尺度熵算法。该算法对传统粗粒化方法进行了改进，改进粗粒化采用滑动均值滤波的形式使各尺度上粗粒化后的数据长度与原始时间序列长度保持一致，减少了随机误差，增加了后续算法的准确性。此外，通过定义模糊隶属函数降低了传统样本熵中对阈值的依赖性，消除了传统方法中存在的不稳定现象。

文中通过数据实验证明了改进多元多尺度熵对正常步态、上楼、下楼步态复杂度的区分效果要优于传统多元多尺度熵，同时说明该算法只需要较少的数据就能对各数据集的复杂度进行很好的区分。因此，此方法可为人体行为的识别、患者的康复治疗提供重要的依据。本文只将改进多元多尺度熵应用于对正常步态、上楼、下楼步态三种行为的识别，如何用该算法对其他多种人体行为进行识别，是本文需要进行的下一步工作。

［1］赵凌燕，张立勋，张今瑜，等.人体步态运动学研究方法进展综述［J］.测控技术，2007，26（12）：1-3.

［2］郭忠武，王广志，高敬，等.正常青年人步态运动学参数的研究［J］.中国康复理论与实践，2002，8（9）：533-536.

［3］苌飞霸，尹军，张和华.一种基于智能终端的人体心电信号监护系统设计［J］.传感技术学报，2014，27（3）：289-292.

［4］钱朋安，吴仲城，葛运建.体育训练用加速度测量装置的研究［J］.传感技术学报，2003，16（1）：13-15.

［5］卢先领，王洪斌，王莹莹.加速度数据特征在人体行为识别中的应用研究［J］.计算机工程，2014，40（5）：178-182.

［6］Heikki Ailisto，Mikko Lindbolm，et al.Indentifuing People from Gait Pattern with Accelerometers［C］//Proceeding of SPIE volume 5779 Biometric Technology for Human Identification II.Bellingham，2005：714.

［7］刘晓婷，曹玉珍.基于加速度的人体步态信息多尺度熵研究［D］.天津：天津大学，2008：19-30.

［8］Maquire D，Frisby R.Comparison of Feature Classification Algorithm for Activity Recognition Based on Accelerometer and Heart Rate Data［C］//Proc of the 9 th IT&T Conference.Dubin，Ireland-Dublin Instetute of Technology Press，2009：22-23.

［9］He Zhenyu，Jin Lianwen.Activity Recognition from Acceleration Data Using AR Model Representation and SVM［C］//Proc of International Conference on Machine Learning and Cybemetics，IEEE Press，2008：2245-2250.

［10］徐川龙，顾勤龙，姚明海.一种基于三维加速度传感器的人体行为识别方法［J］.计算机系统应用，2013，22（6）：132-135.

［11］Acharya U，Molinari F，Sree S，et al.Automated Diagnosis of Epileptic EEG Using Entropies［J］.Biomedical Signal Processing and Control，2012，7（1）：401-408.

［12］徐永红，崔杰，洪文学，等.基于改进多元多尺度熵的癫痫脑电信号的自动分类［J］.生物医学工程杂志，2015，32（2）：256-262.

［13］Costa M，Peng C K，Goldberger A L，et al.Multiscale Entropy Analysis of Human Gait Dynamics［J］.Physica A.2003，330（1）：53-60.

［14］邢秀玉，刘鸿宇，黄武.基于加速度的小波能量特征及样本熵组合的步态分类算法［J］.传感技术学报，2013，26（4）：547-549.

Human Gait Acceleration Signal Classification Based on Improved Multiple Multiscale Entropy*

WANG Xuyao，XU Yonghong
（Institute of Biomedical Engineering，Yanshan University，Qinhuangdao Hebei 066004，China）

Traditional Multiple multiscale entropy algorithm at moment of dealing with time series of limited length，would led to curve fluctuations larger and threshold selection will also have a greater impact on the results.Therefore，on the basis of traditional Multiple multiscale entropy，firstly this paper improved the way of traditional coarsegrained process，the method improved coarse-grained way of traditional multiple multiscale sample entropy by sliding mean filter so that coarse-grained time series equal to the length of original time series on each scale，reduce the compute discreteness of multivariate multiscale entropy.In addition，algorithm both maintain the advantage of hard threshold of multiple multiscale sample entroy and count the distance of two composite delay vector slightly greater than the threshold value by defining fuzzy membership function，not only reducing the dependence of the threshold of multiple multiscale sample entropy，but also solving the instability caused by the traditional threshold.Finally，the algorithm was validated in the emulated data，and applied it to different human gait acceleration signal complexity evaluation and classification.The results show that improved multiple multiscale entropy recognition is better than traditional multivariate multiscale entropy.

gait classification；acceleration signal；Improved multiple multiscale entropy；Traditional multiple multiscale entropy；