嵌入式时栅传感器高精度激励设计*

2015-08-24彭东林陈锡侯

传感技术学报 2015年12期

王　婷，彭东林，武　亮，陈锡侯

嵌入式时栅传感器高精度激励设计*

王婷1，2，彭东林2*，武亮2，陈锡侯2

（1.重庆理工大学机械工程学院，重庆400054；2.机械检测技术与装备教育部工程中心，时栅传感及先进检测技术重庆市重点实验室，重庆400054）

介绍了嵌入式时栅传感器的基本原理，分析了两相激励信号不一致性主要是幅值不等和相位不正交对传感器测量精度的影响。基于DDS原理结合反馈控制设计了高精度的激励信号模块，采用反馈电路控制可程控放大电路调理两相信号幅值，实现了激励信号的幅值相等，基于闭环反馈控制直接修改数字激励信号实现了信号的相位正交。实验研究结果表明，采用这种闭环控制的方法，传感器短周期测角误差从±65″降低到±16″左右，常值误差基本消除，传感器精度大幅度提高。

嵌入式时栅传感器；高精度激励；DDS；可程控增益放大电路；闭环控制

EEACC：7230doi：10.3969/j.issn.1004-1699.2015.12.014

精密位移测量是保证产品质量的重要手段，也是进行科学研究的重要工具，在人类生产和科学研究中大量存在。目前，大部分的精密位移传感器如光栅，其精度主要依赖于栅线刻划精度，时栅是基于“时空转换理论”的新型位移传感器，其将空间位移的测量转换为时间的测量，由于其测量原理的特殊性无需高精度机械分度。

嵌入式时栅传感器［1-2］是一种新型时栅位移传感器，其将被测对象作为转子，结合外置的离散测头实现位移测量。除了沿袭前期时栅传感器［3-4］分辨率高、智能化程度高的优点外，由于采用非接触、非运动状态的离散测头，因此具有体积小、重量轻、结构简单、安装方便的优点，由于基于电磁感应原理，因此具有抗油污粉尘干扰的特点，该传感器能很好地应用于风电行业、大型机械制造等传感器安装受限于空间、环境极端恶劣的工作条件［4］。

嵌入式时栅传感器基于电磁感应原理由两相正余弦激励信号感应输出一路信号，通过解算感应信号的相位得到被测对象的位移，由此可知，激励信号的精度将直接影响传感器的测角精度。现有的正余弦激励产生方法主要有：模拟电路的方法、SPWM（Sinusoidal Pulse Width Modulation）技术、专用集成元件、可编程正弦波振荡器芯片等。陈平等［5］采用模拟电路的方法产生正交的激励信号，通过一个幅值环及两个相位环保证两路信号的幅值误差、正交误差，但这种方法不利于数字控制。谢仁飚等［6］提出将原先用于电机驱动的SPWM技术用于感应同步器的双相绕组激磁鉴相型的驱动方案，但这种方式其信号的模拟解调电路复杂，严重依赖于微控制器的资源。何海龙等［7］将这种基于SPWM的技术的驱动方案用于旋转变压器上。各种专用的集成元件如用于旋变的ML2035系列芯片，其原理同DDS（Direct Digital Synthesizer）技术的基本原理一样，其集成度高，它将电压比较器、数模转换器和低通滤波器集成在一个芯片里面，需要配合控制器，但无法满足苛刻的风电行业及航天产品的使用要求，且价格昂贵。可编程正弦波振荡器芯片如AD公司的AD2S99，但只能通过控制芯片输出特定频率的正弦信号。介党阳等［8］设计了由三个运算放大器及若干个阻容器件，构成频率和幅值可调的正弦振荡电路和幅值调整电路，再由一片功率放大器实现功率放大，使输出的电源信号具有足够的驱动能力，但信号频率及幅值调整需更换电阻电容，手段复杂。本文采用基于DDS数字技术的方法产生激励信号，控制方便可靠，由闭环控制电路保证两相激励信号幅值相等、相位正交。

1　嵌入式时栅传感器基本原理

嵌入式时栅传感器基于“时空转换理论”将空间位移的测量转换为时间的测量，其原理是由两路激励驻波信号感应形成一路行波输出信号，通过采用时钟插补的方法检测及解算输出行波信号的相位，由相位即可解算出转子的位移信息。

嵌入式时栅传感器原理示意图如图1所示。

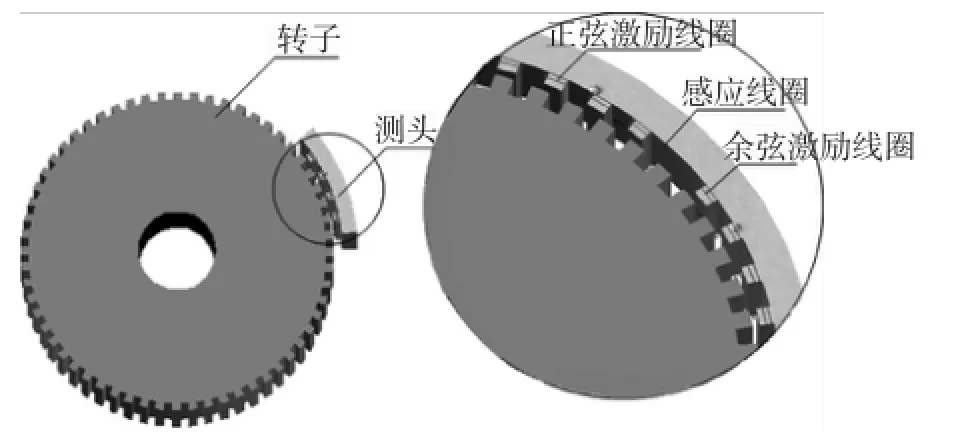
图1　R嵌入式时栅传感器原理示意图

如图1可见，当测头齿（定子齿）与转子齿正对时，气隙磁导最大，随着转子的转动，气隙磁导逐渐增大，当测头齿与转子齿完全错开时，气隙磁导最小，因此，每转过一个转子齿距，气隙磁导变化一个周期，气隙磁导的变化，导致磁路磁通发生周期性变化，信号绕组感应电势也周期性地变化。

由于绕组是同心的绕在测头齿上，因此感应信号绕组的感生电动势与对应的各个齿下的磁导变化有关。适当地选取坐标轴，可以将所有正弦齿及余弦齿下的磁导分别表示为偶周期函数。以第一个正弦齿为例，其齿下的磁导为Λ1，一个周期内Λ1随转角的变化为三角波，可表示为：

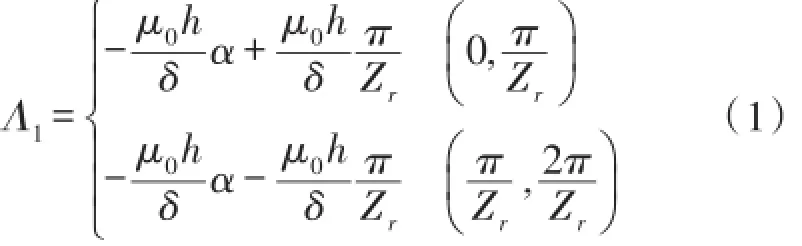
式中，μ0为空气磁导率，h为齿厚，δ为定转子齿间气隙宽度，Zr为转子齿数，2π/Zr为一个转子齿距对应的机械角度值，α为转子相对定子转过的机械角度。

可以看出上式为偶函数，可用傅立叶级数表示。同理可写出定子各个齿下的气隙磁导，将各个磁导分别由傅里叶级数表示为：

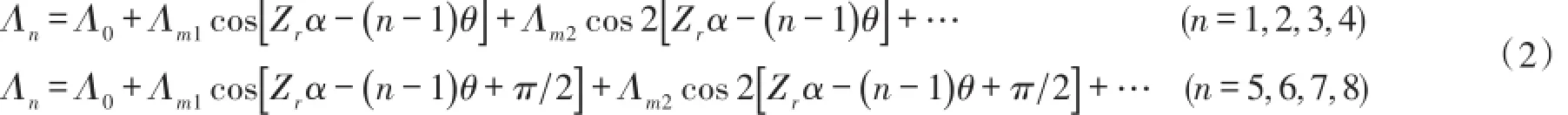
式中，n表示第n个齿下的气隙磁导，下标规定为正弦第一个齿为第1齿，依次类推，则余弦第一个齿为第5齿。Λ0为磁导的恒定分量，Λm为各次谐波幅值，θ=2π（Ws/Wr）表示相邻极靴间的电角度值，为定值，与定转子齿节距比有关。

经计算，上式中主要成分是基波分量，其他各次谐波分量很小，因此可以近似认为磁导是角位移α的正余弦函数，即

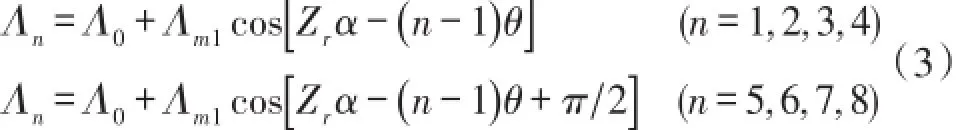
由F=Ni=ΦRm,Rm=1/Λm可知，各个齿下的磁势恒定不变，则磁通随转角变化的规律同气隙磁导随转角的变化规律，即：

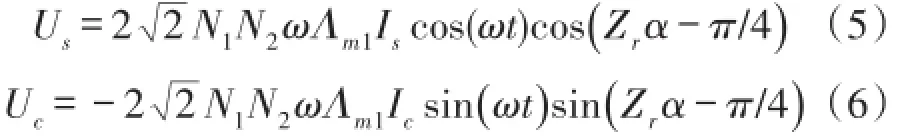
式中，N1、N2分别为每齿上激励绕组和感应绕组匝数。由Is=Ic=I，感应绕组总的感应电势为：

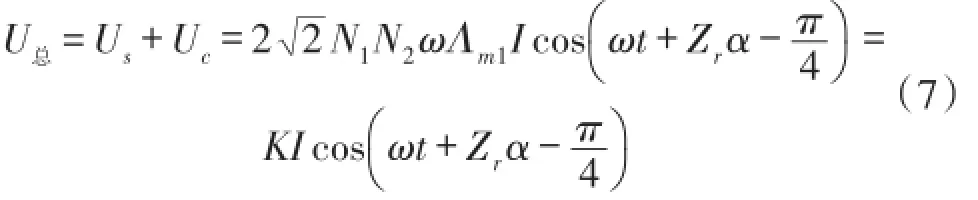
由式（7）知，通过解算感应信号的相位即可求得转角α的值。

2　激励信号不一致性对测角精度的影响

嵌入式时栅传感器是基于电磁感应原理，因此，电气误差的存在将不可避免地影响传感器的精度。这里进一步分析激励信号的不一致性主要是两相激励信号幅值不等、相位不正交对传感器测角精度的影响［9-13］。

①两相激励信号幅值不等带来的测角误差分析

上述式（5）、式（6）中，若两相激励信号幅值不等，即Is≠Ic，当两相激励信号的幅值存在相对误差ε时，其信号的复数形式可表示为：

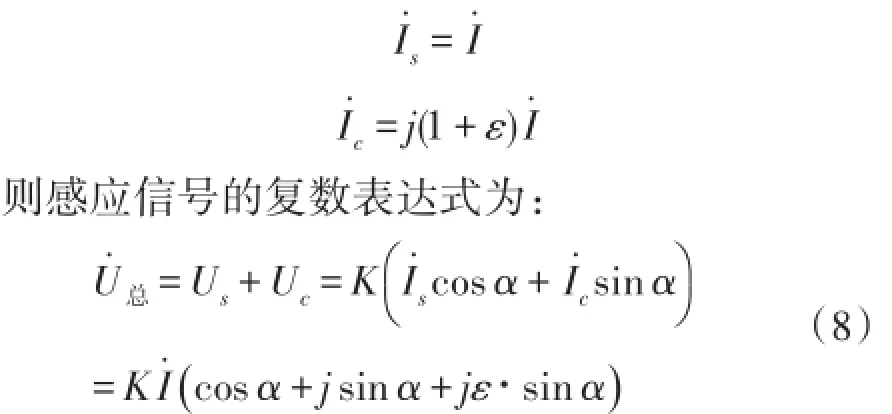
上式在复平面上表示为图2所示。

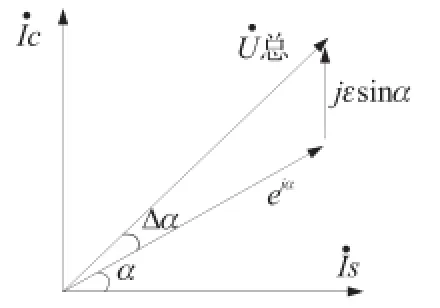
图2　R激励信号幅值不等测角误差向量图

由上图可得，由于幅值的微小误差，导致感应信号的相位角误差为Δα，

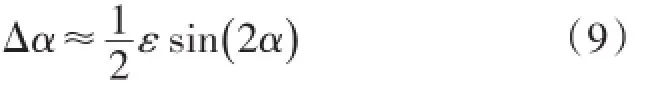
由式（9）可以看出，由于激励信号的幅值不等，将使感应信号相位存在短周期二次正弦误差，其幅值是激励信号幅值误差的一半，从而将使传感器存在二次测角误差。

②两相激励相位不正交带来的测角误差分析

上述式（5）、式（6）中，若两相激励信号相位不正交，即余弦相相对正弦相有相位误差ε，设激励信号为：

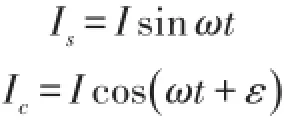
则激励信号表示为复数形式如下：

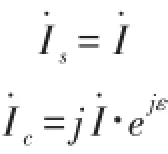
则感应信号的复数表达式为：

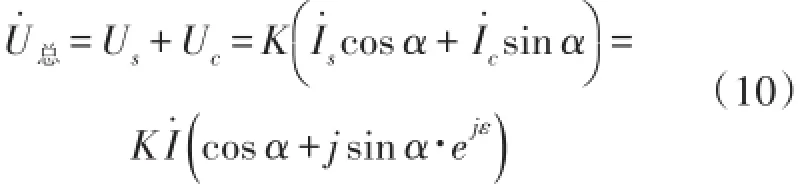
根据欧拉公式ejε=cosε+jsinε，由于正余弦信号相位误差ε是极小量，故：

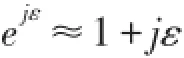
因此式（10）可写为：

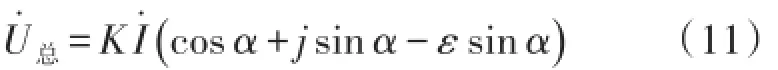
上式在复平面上表示为图3所示。

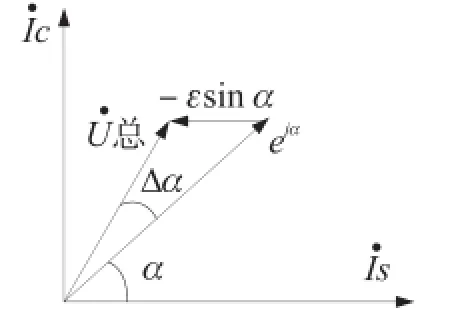
图3　R激励信号不正交测角误差向量图

由图3可得，由于正余弦激励信号的微小相位误差，导致感应信号的相位角误差为Δα，

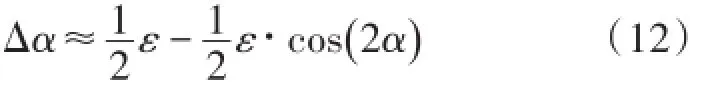
可以看出，由于激励信号相位不正交，将使感应信号相位存在短周期二次余弦误差和一个常值误差，直接导致传感器存在常值误差和一个二次余弦误差。

3　高精度激励设计

由于两相激励信号幅值不相等，相位不正交必然会造成传感器的测角误差，为提高传感器测量的精度，设计了高精度激励信号模块，采用基于DDS数字技术结合闭环控制电路产生高精度激励信号，采用可程控放大电路调理两相激励幅值，实现了激励信号的幅值相等，采用闭环反馈控制的方法实现了信号的相位正交。

DDS信号具有频率分辨率高、波形稳定性好、精度高的优点，且频率、相位、幅值方便可调，因此，传感器激励信号将采用基于FPGA的DDS信号发生器来产生高质量的正余弦信号。但是在两相激励传导的过程中，由于数模转换电路的转换误差、滤波及放大电路干扰和其它外界干扰的存在，导致两相激励信号幅值不等，因此余弦相功放部分采用可程控增益放大电路，信号经采样送入DSP进行幅值比较后返回幅值修正系数，调节余弦相的幅值最终使两相激励幅值相等。考虑到相位不正交的误差可能是来源于时钟源的波动及正余弦线圈感抗不匹配，因此，信号经采样后经DSP芯片采用时钟插补的方法鉴相，由DSP芯片输出相位补偿参数反馈给FPGA，调节余弦相相位使两相信号正交。综上，基于DDS原理的高精度激励信号产生原理框图如图4所示。

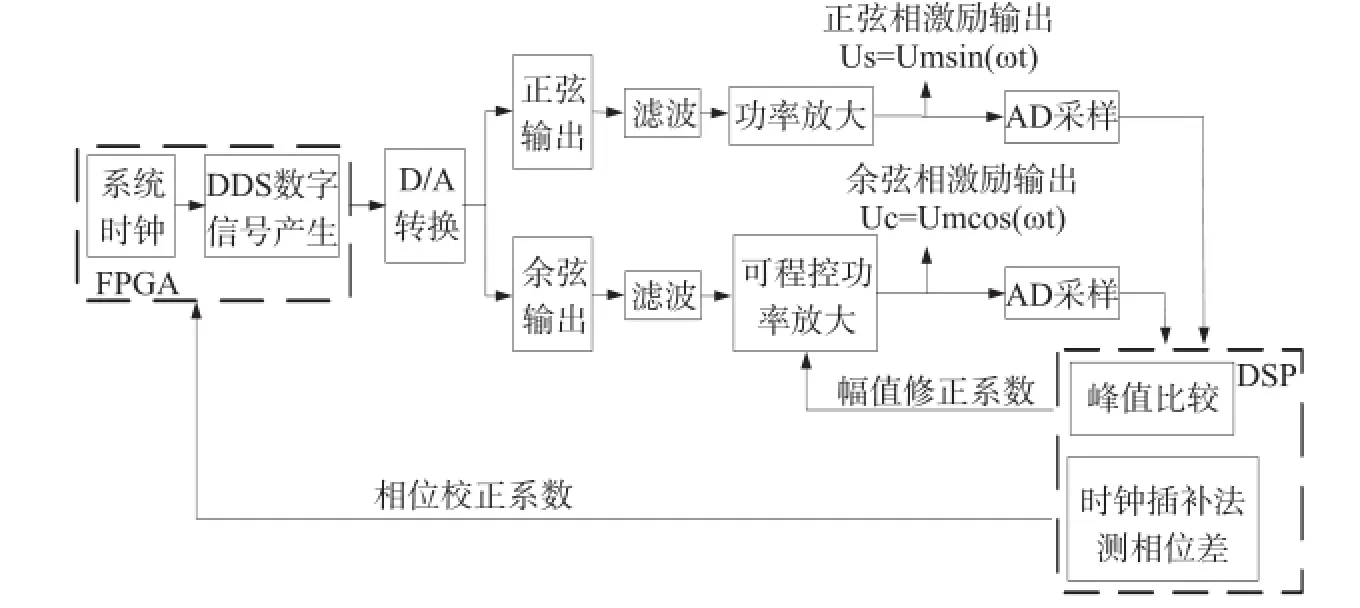
图4　R高精度激励模块原理框图

3.1正余弦信号的产生

正余弦激励信号产生的具体方法是：在FPGA的内部建立一个正弦信号数据表，在外部时钟的驱动下，读取正弦信号数据表中的数据，送到高速DAC中进行数模转换，再经滤波放大得到正余弦激励信号。

①FPGA部分

FPGA芯片选用EP2C8T144I8N，其内部的正弦信号数据表有480个正弦数据点，在外部时钟的驱动下输出离散数字正弦信号到数模转换芯片，并控制D/A芯片输出407 Hz的模拟正余弦激励信号，此外，FPGA接收来自DSP的相位校正系数，控制D/A芯片对余弦相的相位进行校正以保证两相信号的正交性。另外，FPGA芯片还产生脉冲插补比相所用的脉冲信号。激励信号产生部分主要是基于FPGA芯片利用VHDL语言实现DDS信号产生，FPGA部分的结构框图如图5所示。

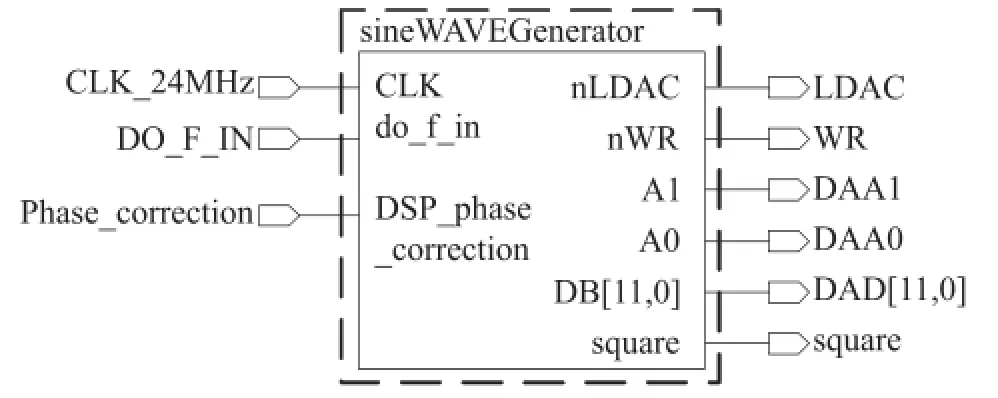
图5　RFPGA产生正弦波结构框图

②数模转换

12位高性能的D/A转换芯片AD5344BRU将FPGA输出的数字信号转换为模拟信号输出，芯片的基准电压由电压基准芯片ADR440BRZ产生。D/A转换芯片输出的正弦波信号经高精度运放OPA4277放大。

③滤波及功率放大

由于所需激励信号是407 Hz低频信号，所以后续的滤波电路采用一阶RC低通滤波，其截止频率为440 Hz；后接跟随器OPA4277，其作用是阻抗匹配，使AD8397的输入阻抗对输入信号的影响最小；最后，信号经轨到轨、高输出电流放大器AD8397ARDZ放大产生最终的激励信号。

3.2激励信号相位控制

模拟正余弦输出信号经采样芯片AD7356采样并通过DSP芯片处理，AD7356是双通道12位高吞吐率的采样芯片，AD8138差分放大器将正余弦激励信号SA、SB转换为差分信号输入AD7356，运用DSP芯片TMS320C30-40强大快速的数据处理能力，实现对两路采样信号的鉴幅处理，并通过补偿余弦相幅值误差使两路信号幅值相等；另外，采用时钟插补的方法检测余弦相的相位误差并实现误差修正以使两路信号完全正交。其电路图如图6所示。

3.3激励信号幅值控制

余弦相功率放大部分和正弦相功率放大部分稍有不同，其功率放大芯片的反馈电阻采用的是数字电位计AD5141，可通过DSP返回的信号配置AD5141芯片以调整反馈电阻的阻值，达到调整输出信号幅值的作用，使两相信号幅值相等。AD5141是单通道、非易失性数字电位计，阻值10 kΩ，8位阻值分辨率，线性增益设置模式可实现电阻匹配精确，其幅值调整的最小步距为3.9‰，阻值通过SPI兼容数字接口设置，因此能够直接和DSP芯片直接进行通信。具体接线图如图7所示。

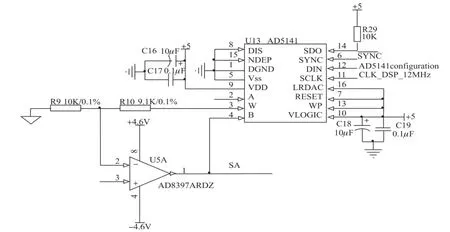
图6　R采样及数据处理电路图

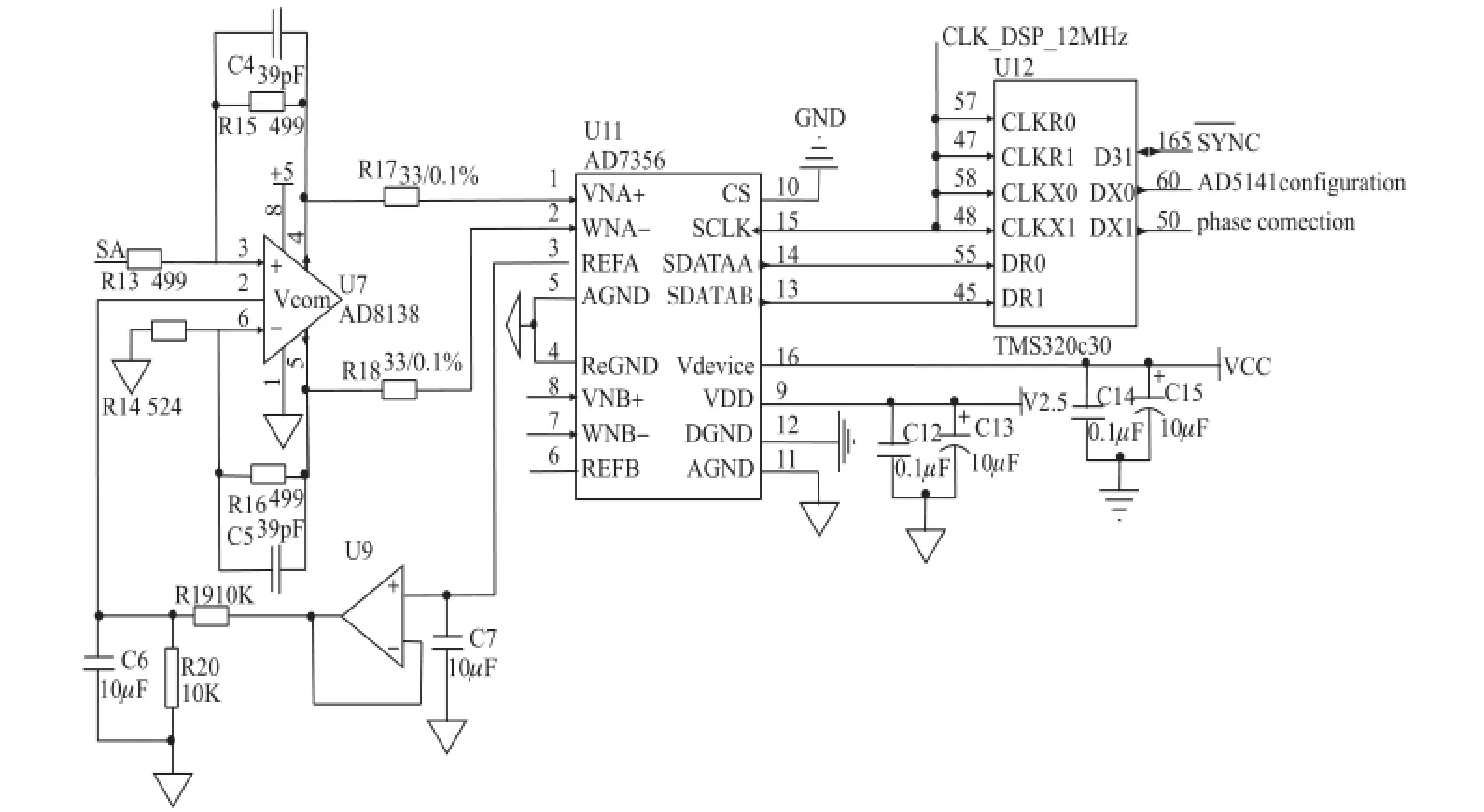
图7　R可程控增益放大器

4　实验分析

为了验证上述方法的可行性，搭建了如图8所示的实验平台。

实验系统以德国海德汉HEIDENHAIN高精度光栅（精度±1″）作为基准量具来检定时栅传感器的精度，时栅和光栅分别通过弹性联轴节安装在分度转台的主轴上。由控制系统控制驱动电机带动转台做匀速转动，为了使转台平稳匀速转动，系统将光栅测角值反馈给运动控制卡而构成闭环控制。时栅和光栅的输出信号经硬件平台实时同步采集并处理后，通过串口输送至上位机进行数据处理、误差计算及结果显示。

由示波器观察激励信号的波形图，如图9所示。由图9（a）测量结果显示部分可以看出，两相激励信号频率在400 Hz左右；信号的幅值和相位均存在较大的波动，可以看到，幅值不相等，正弦相信号幅值2.85 V，余弦相信号幅值2.96 V；两者相位差约2°，差异比较明显。如图9（b）所示，采用DDS技术加闭环控制的方法后，激励信号得到改善，其幅值差、相位差均变小，正弦相幅值与余弦相幅值相等，正交性变好，相位差异不明显。

图8　R实验平台

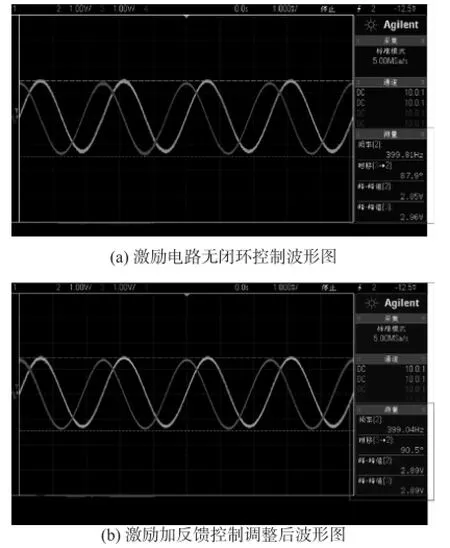
图9　R激励波形图

将时栅和光栅的输出信号经硬件平台及上位机处理后，得到时栅角位移测量值及误差值，实验中采用400对极的嵌入式时栅传感器，单个对极对应角度54′，对极内的误差形式为短周期误差，取一对极内的测角误差数据进行分析，图10为激励加反馈控制调整前后的传感器测角误差曲线。

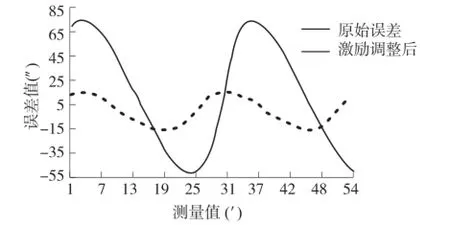
图10　传感器单对极内测角误差曲线图

图10R所示为一个对极内常值误差与二次测角误差曲线。可以看出，激励调整前二次误差峰峰值约为±65″，常值误差约14″，与上述激励信号不一致性对传感器测角精度影响的分析结果一致，通过采用闭环控制调整激励后，二次误差峰峰值变为±16″，常值误差基本消除，传感器短周期误差提高了75%。

5　结束语

本设计基于FPGA产生DDS正弦信号，信号频率分辨率高，波形稳定性好、波形平滑，并采用闭环控制来消除两相信号幅值不等误差、相位不正交误差，最终产生高精度的激励，有效地降低了嵌入式时栅角位移传感器的短周期误差。

［1］孙世政，彭东林，付敏，等.提高嵌入式时栅传感器精度的测头设计方法［J］.仪器仪表学报，2015，36（1）：26-31.

［2］彭东林，李彦，付敏，等.用于极端和特殊条件下机械传动误差检测的寄生式时栅研究［J］.仪器仪表学报，2013，34（2）：359-365.

［3］武亮，陈锡候，王阳阳.磁导调制型时栅位移传感器测量方法研究［J］.传感技术学报，2014，27（8）：1043-1048.

［4］杨伟，彭东林，朱革，等.基于变耦合系数变压器原理的时栅位移传感器设计［J］.仪器仪表学报，2006，27（11）：1403-1405.

［5］陈平，罗晶，王毅，等.反馈控制感应同步器双相激磁电源研究［J］.中国惯性技术学报，1997，5（1）：54-57.

［6］谢仁飚，张明涛，刘银年，等.正弦波脉冲调制在空间用感应同步器驱动技术中的应［J］.测试技术学报，2009，23（1）：74-77.

［7］何海龙，刘世挺，高栋.基于正弦脉冲宽度调制SPWM的旋转变压器激磁电路［P］.中国专利，101567658.2009-10-28.

［8］介党阳，倪风雷，顾义坤，等.旋转变压器的励磁电源电路［P］.中国专利，101714821A.2010-05-26.

［9］Hwang S H，Kim H J，Kim J M，et al.Compensation of Amplitude Imbalance and Imperfect Quadrature in Resolver Signals for PMSM Drives［J］.IEEE Transactions on Industry Applications，2011，47（1）：134-143.

［10］Hanselman D C.Resolver Signal Requirements for High Accuracy Resolver-to-Digital Conversion［J］.IEEE Trans on Industrial Electronics，1990，37（6），556-561.

［11］Du Chunyang，Yang Guijie.Error Analysis and Compensation for Inductosynbased Position Measuring System［R］.38thIndustry Applications Conference Annual Meeting，2003，1：6-10.

［12］刘小康，彭凯，王先全，等.纳米时栅位移传感器的理论模型与误差分析［J］.仪器仪表学报，2014，35（5）：1136-1142.

［13］王先全，雷毅谈，张虹光，等.基于DSP的时栅位移传感器误差在线处理与系统设计［J］.传感技术学报，2014，27（8）：1054-1059.

High-Precision Excitation Design Method for Embedded Time Grating Sensor*

WANG Ting1，2，PENG Donglin2*，WU Liang2，CHEN Xihou2
（1.Chongqing University of Technology，College of Mechanical Engineering，Chongqing 400054，China 2.Engineering Research Center of Mechanical Testing Technology and Equipment，Ministry of education Chongqing Key Laboratory of Time-Grating Sensing and Advanced Testing Technology，Chongqing 400054，China）

The basic principle of embedded time grating sensor was introduced，and the influence of accuracy caused by two excitation signals with variable amplitudes and non-orthogonal phases was analyzed.Based on DDS and feedback control the excitation signal generator with high precision was designed.The programmable-gain amplifier was used to modulate the amplitude of two excitation signals，which achieved equal amplitude，and the orthogonal signals were realized through the feedback control method.The experimental results show that the short-period error has been reduced from±65″to±16″，and the constant error has been basically eliminated by using this closedloop control method.The accuracy of the sensor have been greatly improved.

embedded time grating sensor；high-precision excitation signals；DDS；programmable-gain amplifier；closed-loop control