关于虚功变量的一种典型分析

朱 峰，林凯颖

(西南交通大学电气工程学院，四川成都 610031)

0 引言

尽管磁场力可通过洛伦兹公式求得。但由于实际计算中往往遇到复杂的积分运算，因此，通常从磁场能量出发，计算场中载流体所受磁场力更为有效，此即虚功原理［1-3］。虚功原理的应用首先要建立广义坐标系，选取广义坐标。广义坐标是确定系统中各导体形状、尺寸与位置的一组独立几何量。企图改变对应的广义坐标的力就是广义力。

在能量体系确定的条件下，虚位移量的选取是运用该方法的关键。对比的分析方法能使问题的本质更加明了。本文通过一个典型例题，采取不同的物理视角，对应了不同的虚位移参量，从而使得到的广义力也具有不同的物理含义。另外，通常电磁场相关教材中不建立坐标系，直接对参量进行求导，使得解题显得不规范。本文通过建立坐标系的方法使得解题过程更加明了。该分析方法对于学生提高运用数学能力、理解虚功原理的本质及应用具有一定的帮助。

1 问题的提出

设有一对长直导线，长导线回路中通有电流I1，回路中放置一不变形的线框，线框中通有电流I2，具体布局如图1所示。线框宽为b，高为c;两长直导线轴线中心相距D，线框最左边距左导线中心a，导线半径均为R。利用虚位移法求线框受力。

图1 一对长直导线中载流框布局

2 问题的分析

2.1 基于单边的虚位移分析

无论对线框作何种分析，我们第一步都要先建立坐标系。如图1所示，以一根导线圆心上任意一点为原点，横轴为x轴，纵轴为y轴。由于左右两边导线在距左导线为x处产生的磁场应强度同方向。则距左直导线x处的磁感应强度为

在线框处取一宽为dx的微元，外导线回路对线框互感磁链为

所以它们之间的互感系数为

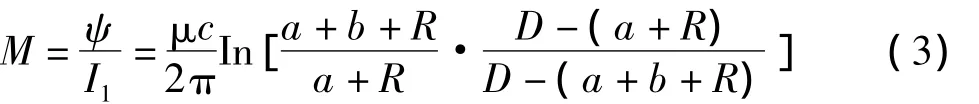
因为只考虑外导线对线框的作用，所以计算磁场能量时只需考虑互感磁链［6］。故可求得此时线框中的互感能量为

虚功原理的基本思想是先假设某个载流体只有一个广义坐标发生变化［2］。为便于下面的分析，我们先将闭合线框分成4部分，分别为12边，23边，34边以及14边。对于12边，其对应的广义坐标为x1=a+R;同理，23边位置表示为y1;34边为x2=a+b+R;14边位置表示为y2。

在坐标系下，互感能量式(4)可表示为

以下利用虚功受力公式 fg= əWm/əx|I1，I2=C，即可计算各边受力。

(1)12边受力:由于虚功原理的基本思想就是假设除了某个载流体外其余载流体不动。所以此时线框中只有12号边的x1发生微量变化，其余边不动。此时的虚功变量是x1。又因为其他载流体的位置都不发生变化，所以此时x2、y1、y2为常量。因此，有

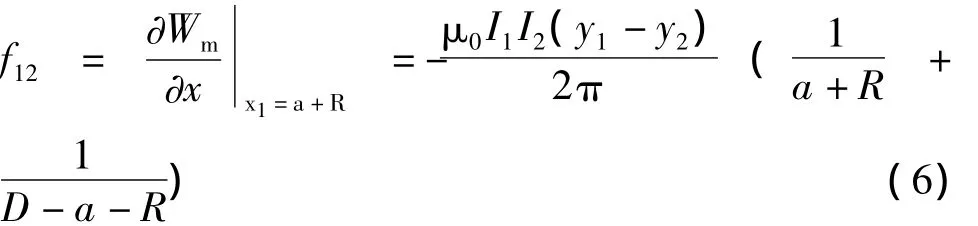
这里，正号表示与坐标轴正方向相同，负号表示与坐标轴正方向相反。式(6)表示此时线框向左受力。

(2)34 边受力，此时虚功变量为 x2，x1、y1、y2为常量，所以

(3)对于23边和14边，其所受的力使边框在y方向上移动，所以其虚功变量分别为y1、y2。即有

式(8)为正，表示此时受力向上;式(9)为负，表示此时受力向下。

为了验证我们得到的答案正确与否，下面用洛伦兹力验证。

力的方向水平向左。这与基于单边的虚功原理求得的答案式(6)相同，所以该方法是正确的。同理，23、34、14边也可证得有类似的结果。

2.2 基于整体移动的虚位移分析

与上面的方法不同，我们现选取整个线框进行受力分析，由于线框是不变形的刚体，所以整体线框的位置可以用x=a+R(左边框的位置坐标)，y1=y2(下边框的位置坐标)表示。也就是说，假设整个线框可以沿某个方向发生微动。将该移动方向沿x、y方向分解，即可确定整体线框沿该方向的受力。

当有x方向的力作用在线框上时，x为此时的虚功变量，整体框沿方向移动，则根据式(4)，有

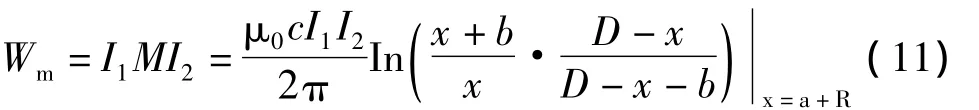
因此，有

这恰好为式(6)和式(7)相加得到的结果，从物理意义上说，线框水平方向受力就是两边受力之和，验证了该方法的正确性。

当有y方向的力作用在线框上时，y为此时的虚功变量，整体框沿y方向移动，则

有

这说明整框在垂直方向受力为零，而式(8)、(9)所表示的23边、14边受力大小相等、方向相反，叠加结果自然为零，从物理意义上说，线框垂直方向受力就是两边受力之和，验证了该方法的正确性。

此外，本方法中线框的位置也可选择右线框的位置坐标和上线框的位置坐标来表示，即x=a+b+R，y=y1。分别对它们进行求导，求得的结果是一样的。

这里还需要着重指出的一点是，一般教材中，计算受力时直接对参量进行求导。例如计算12边受力时，运用式(4)，应求得的解为

但是这里存在一个问题，式(4)中有4处均有x=a+R，若都求，则求得的是式(12)，表示的是整个框的水平力，但这样求解就出现错误了。故笔者认为该方法概念不明确。建立坐标系的方法会使解题更加明了。

4 结语

通过上述两种分析，可以看到站在不同的物理角度，虚位移量的选法不同，其对应的力的物理含义也不同。但都遵循以下原则:

(1)参量可以有不同的物理意义，若表征各边参量，对应的虚功力为各边受力;若参量表征的是整体系统，则受力是整体受力，且整体与各边有着辩证关系。

(2)因为微动而发生变化的位置坐标为此时的虚位移量，其他为常量。单边移动时，其他边的位置为常量。

(3)用坐标表示，可以使解题更加明确。

抓住这三个原则，会使学生对虚功原理的应用更加熟练与灵活。

参考资料:

［1］ 王泽忠，全玉生，卢斌先.工程电磁场［M］.北京:清华大学出版社，2004

［2］ 冯慈璋，马西奎.工程电磁场导论［M］.北京:高等教育出版社，2000

［3］ 雷银照.电磁场［M］.北京:高等教育出版社，2008

［4］ 朱峰，李春茂.分布电容和分布电感比拟关系的严格推证［J］.南京:电气电子教学学报，2006.12.28(6):13-17

［5］ 朱峰，魏天彩.静电场中导体镜像与介质镜像的统一［J］.南京:电气电子教学学报，2012.2.34(1):102-104

［6］ 朱峰，杨晓铖.基于能量守恒定律的载流体内自感分析［J］.南京:电气电子教学学报，2013.2.35(1):17-19