中国要素增强型的内生技术变化:1985~2012
2015-08-22袁鹏,叶鑫
袁 鹏,叶 鑫
(1.西南财经大学 工商管理学院,成都 611130;2.大连理工大学 管理与经济学部,辽宁 大连 116024)
中国要素增强型的内生技术变化:1985~2012
袁 鹏1,叶 鑫2
(1.西南财经大学工商管理学院,成都611130;2.大连理工大学管理与经济学部,辽宁大连116024)
通过对要素效率的内生化设定,并建立要素增强型的内生技术变化模型,对1985~2012年期间中国资本、劳动和能源对技术变化的作用进行了实证分析,并考察了技术变化的演进趋势和来源,分析结果表明:研发、进出口、FDI、人力资本和基础设施等因素对三种要素的效率演进具有不同影响;技术进步是推动中国经济增长的重要力量,而其主要来源为劳动效率和能源效率的提升所导致的增强型技术变化;资本效率下降所致的负向技术变化对技术进步起到了抑制作用;劳动增强型技术变化和资本负向技术变化主要来自于技术效应,能源增强型技术变化主要来自于价格效应;规模效应对所有要素的技术变化影响均较小。
内生技术变化;要素增强型;要素效率
改革开放以来,中国的经济增长引人瞩目。有关中国经济奇迹背后的驱动因素成为学术界讨论的热点话题。特别是关于生产率增长或者技术进步作用的讨论十分热烈,因为这一问题事关中国经济增长的可持续性。由于要素边际报酬递减的作用,持续的经济增长唯有依靠生产率增长或者技术进步。大量的国内外实证文献从行业、地区、企业等层面考察了全要素生产率(TFP)增长或技术进步在不同时期中国经济增长中的作用,但未获得一致结论。[1]
虽然现有研究加深了我们对中国经济增长的认识,但其普遍存在的一个局限是关于Hicks中性技术变化的假设。在这一假设下,技术变化对所有生产要素的效率具有相同作用,并且各要素在成本中的份额将保持不变。然而就中国而言,一个明显的事实是,最近20年来,劳动报酬在GDP中的份额持续下降,而资本报酬的份额却持续上升。这实际上暗示了技术变化可能是非中性的,即技术变化对不同要素的效率具有不同的影响。近年来,在非中性技术变化的假设下,少数研究针对中国经济,估计了资本和劳动的效率变化率,发现两种要素的效率变化具有明显差异,[2][3]不过,这些研究均将技术变化视为外生的,没有考虑相关因素在要素效率变化过程中的作用。此外,现有研究通常只考虑了资本和劳动两种要素,而忽视了其他一些重要的生产要素,特别是能源。中国面临越来越严重的能源约束,在考察中国技术变化的时候,将能源这一关系国计民生的生产要素纳入研究视域是十分必要的。
针对以上不足,本文试图在以下两个方面扩展现有研究:第一,摒弃了中性技术变化的假定,采用要素增强型技术变化模型,将能源纳入技术变化的测度框架,考察要素之间效率演进的差异,以及要素效率变化对总技术变化的贡献;第二,将技术变化进行了内生化处理,更有利于识别人力资本、研发、国际贸易与外商直接投资、基础设施等多种经济因素在要素效率演进中的作用。
一、要素增强型的内生技术变化模型
在要素增强型技术变化模型基础上,[4]我们对要素效率进行了内生化处理,设定如下内生化的技术变化模型:
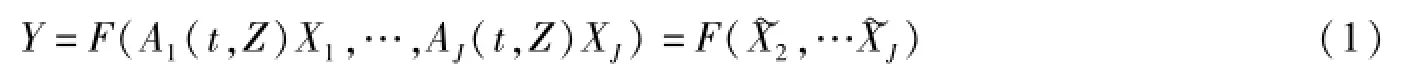
其中,F(·)表示生产技术水平,Y代表产出,Xj表示第j种要素投入(j=1…,J);Aj(t,Z)>0,表示第j种要素在t年的效率,以下简写为Aj。除时间趋势变量t外,Aj还受到一组外生经济变量Z的影响,这一设定将Aj内生化=AjXj代表要素j的有效投入。如果Aj增大,意味着要素效率提高,从而实现投入不变,而产出增加。若∀j有Aj=A,且生产函数为线性齐次的,那么技术变化是希克斯中性的。以上生产结构使得要素特定的技术变化能够被区分出来,从而能够衡量特定要素对总技术变化的贡献。事实上,要素特定的技术变化和总技术变化可能具有不同的,甚至相反的趋势。
总技术变化可以表示为:
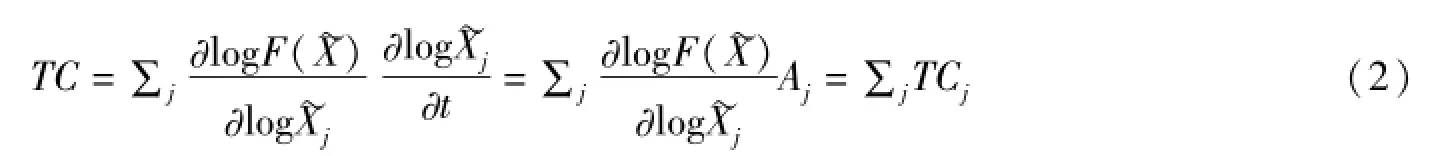
其中,Aj=∂log∂t=∂logAj/∂t,TCj=∂logF(~Xj)/∂log~Xj·Aj。在变量名上方加点“·”,表示该变量随时间的变化率。从TCj表示要素 j的技术变化,体现了该要素的效率变动对总技术变化的贡献。Aj和 ∂logF (~x)/∂log~Xj,分别表示要素j的效率变化和完全竞争市场条件下要素j的成本份额。(1)式所示生产函数的对偶成本函数可以写成:C=C(~P,Y)。C是要素投入的总成本(C=∑jPjXj),Pj表示要素j的实际价格,~Pj= Pj/Aj,表示要素j的有效价格。一种要素效率提高意味着它有效价格下降(~Pj)。在成本函数框架下,技术进步TC定义为:TC=Shephard引理,S=∂logC/∂logP~=P~X~/C=PX/C,故Sj的成本份额。

其中,j。根据jjjjjjj表示要素因此,根据(3)式,总技术变化是各要素效率变化和其成本份额的加权平均值。(3)式与(2)式所定义的总技术变化是相同的。现在我们设定成本函数的具体形式为如下超越对数成本函数:
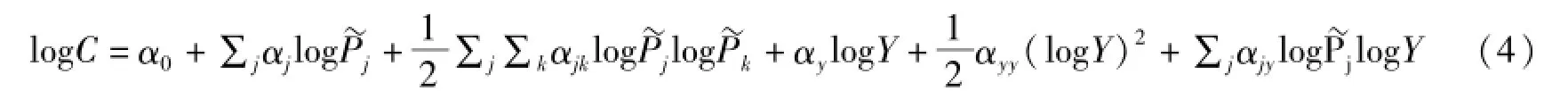
其中,j,k=K,L,E,K、L、E分别表示资本、劳动和能源。根据谢泼德引理,得到要素份额方程的具体形式为:

将份额方程(5)带入(3)式,整理后得到:
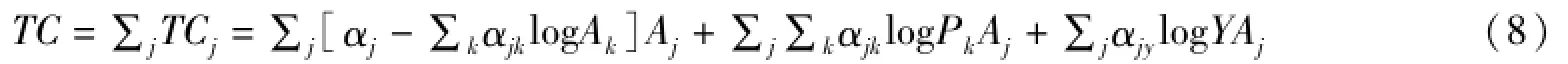
(6)式表明,技术变化可以分解为三个部分:第一项表示纯技术变化,称之为技术效应;第二项表示价格诱致的技术变化,称之为价格效应;第三项表示规模引致的技术变化,称之为规模效应。
如前所述,除时间趋势变量外,要素效率或生产率还受到一组外生变量的影响。本文主要考虑了研发(RD)、人力资本(HR)、出口(EX)、进口(IM)、外商直接投资(FDI)、基础设施(IF)等外生变量,并设定要素效率的具体函数形式为:
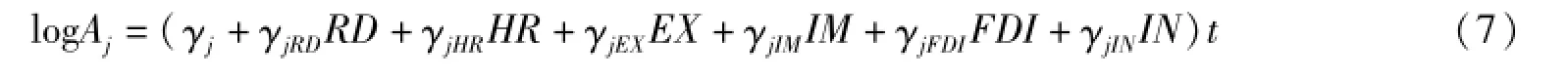
其中,γj为常数项,用以表示自发的要素效率变化,它只受时间的影响,而与上述其他经济变量无关。通过外生变量的引入,要素效率得到了内生化。根据A·j=∂logAj/∂t,得到:
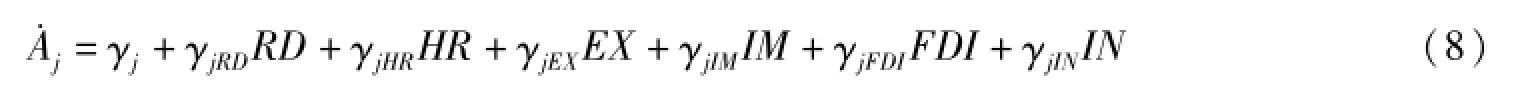
二、数据说明
本文采用了1985~2012年期间29个中国省域(直辖市、省和自治区)地区的面板数据,样本中未包含港澳台地区和西藏自治区,重庆与四川进行合并处理。基础数据来源于相应年份的中国统计年鉴、中国能源统计年鉴,以及新中国55年、60年统计资料汇编。
产出Y采用地区生产总值表示。劳动价格PL以收入法计算的地区生产总值中的劳动者报酬与从业人数之比来表示。资本价格PK的计算公式为:资本价格 =(地区生产总值 -劳动者报酬)/实物资本存量。[5]实物资本存量采用永续盘存法进行核算,公式为Kt=Kt-1(1-δ)+It。下标 t代表第t年,I表示投资,δ为折旧率,K0为期初实物资本存量。对于It,本文采用的是固定资本形成额的时间序列,并用固定资产投资价格指数换算为1985年的不变价格。由于1990年之前的固定资产投资价格指数没有官方的统计数据,我们采用固定资本形成隐含平减指数代替。①借鉴张军等人的方法,研究期间所有省份采用9.6%的折旧率。[6]K0采用Hall和Jones[7]的方法估计,即K0=I0/(θ+δt)。其中,I0为期初投资,θ为1985~2012年投资的年平均增长率。
分省的能源价格PE并不能直接获得。我们借鉴陶小马等[8]的方法,采用《中国物价年鉴2004》公布的2003年36个大中城市分能源品种的价格数据(以省会城市的能源价格表示其所在省份的能源价格),以及分省的燃料动力类价格指数序列(1986-2012年)进行推算。
地区生产总值,以及要素价格均采用GDP平减指数进行价格平减,转换为以1985年价格表示的可比价。经济运行的总成本等于资本、劳动和能源三种要素的支出总和。各地区的能源支出等于能源投入量(以标准煤计)与能源价格的乘积。研发强度(RD)采用各地区的研发资本存量与实物资本存量的比重来表示。研发资本存量(RDS)一般也采用永续盘存法进行核算,[9]公式为:RDSt=RDSt-1(1-σ)+rdt。rd表示研发支出,以各地区科技活动内部支出来衡量,并通过一个构造的研发价格指数换算为1985年的不变价格。研发价格指数的构造参考了吴延兵的方法,[10]以消费者价格指数和固定资产投资价格指数的加权平均值来表示。权重分别为研发支出中的劳务费份额和固定资产构建费份额。σ为折旧率,参照通常的做法,取值为0.15。RDS为期初的研发存量,借鉴期初实物资本存量的计算方法,其计算公式为:RDS0=rd0/(σ+g)。rd0为期初的研发支出,g为研究期间研发支出的年均增长率。
人力资本水平(HR)采用各地区本专科在校学生人数与总人口的占比来衡量。出口强度(EX)、进口强度(IM)分别用各地区出口额、进口额占地区生产总值的比重来表示。外商直接投资(FDI)采用各地区的外商直接投资存量与实物资本存量的比值来衡量,外商直接投资存量与实物资本存量的核算方法相同。基础设施(IN)是地区经济环境的重要组成部分,其包含的范围很广,事实上难以用单一指标来衡量,本文采用人均货物周转量作为基础设施的代理变量。人均货物周转量体现了一个地区交通运输的发达程度,其值越高,反映出基础设施越完善。
三、结果分析
1.估计结果
在成本方程(4)和份额方程(5)的右边加上经典误差项,组成了一个包含J+1个方程的系统方程组。该系统方程组采用非线性迭代似不相关回归技术估计参数(NISUR)。所有要素的份额方程加总等于1,这将导致误差项的方差-协方差矩阵为奇异矩阵,因此需要去除一个要素的份额方程。由于当估计结果产生收敛的时候,NISUR等价于极大似然法,因此去掉任何一个份额方程并不影响估计结果。在本文中,我们选择去掉能源份额方程。我们首先估计了包含所有要素效率影响因素的系统方程组I,表1、表2分别给出了成本与份额方程、要素效率方程的参数估计结果。成本方程的绝大部分参数都通过了常见水平的显著性检验。成本方程、资本份额方程和劳动份额方程的R2,都非常高,分别为0.978、0.976、0.981。
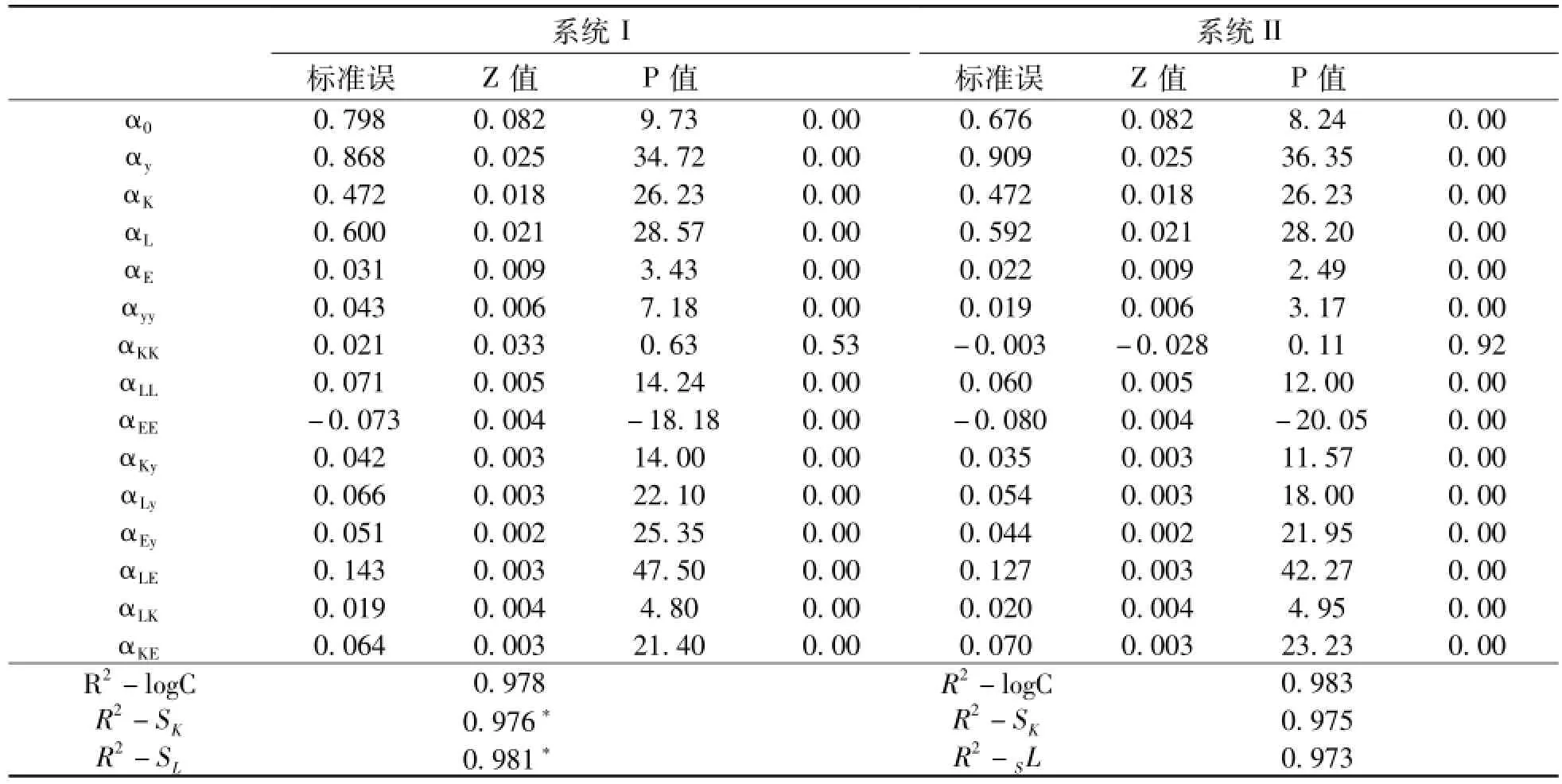
表1 成本与份额方程的估计结果
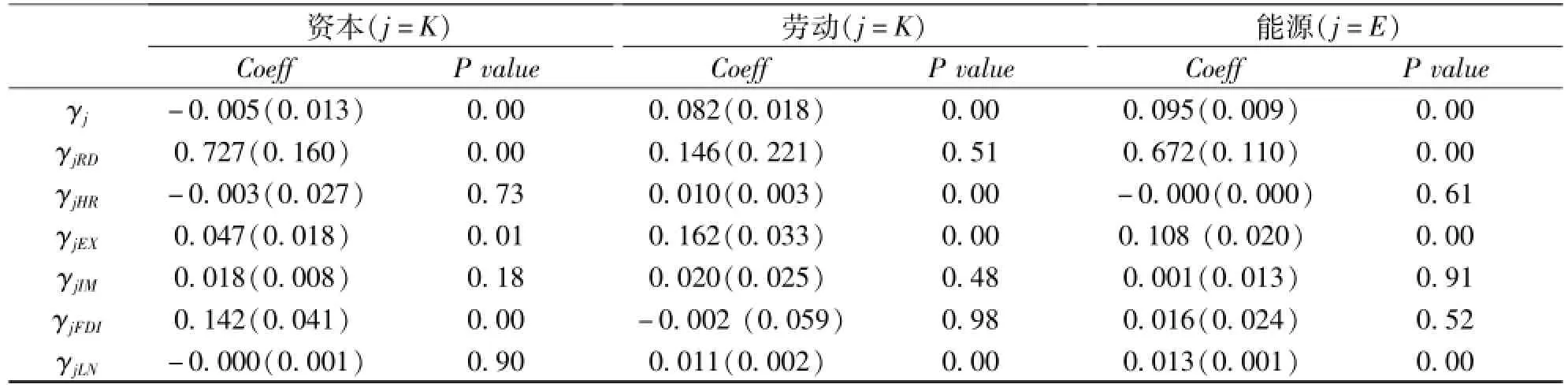
表2 要素效率方程的估计结果(系统 I)
要素效率方程(系统I)的估计结果显示,同一种因素对不同要素的效率具有不同的,甚至相反的影响。为了提高估计的效率,我们剔除了要素效率方程中不显著的影响因素,估计了系统方程组II。成本方程和要素效率方程的估计结果分别见表1、表3。结果显示,除个别参数没有通过10%的显著性检验外,成本方程的其他参数和要素效率方程中的所有参数都通过了1%的显著性检验,且估计结果接近于系统方程组I。成本方程、资本份额方程和劳动份额方程的R2也都超过了0.97。

表3 要素效率方程的估计结果(系统 II)
2.要素效率的变化与影响因素分析
以要素效率方程(系统II)的估计结果为基础,我们计算了要素效率的变化率。结果表明,研究期间,三15.2%以上,且呈现出波动向上的增长趋种要素的效率变化具有明显差异。劳动效率的增长率()保持在势,最高超过17.9%,年均为16.7%。能源效率的增长率(A·ε)也为正,年际间略有波动,但基本上保持在7.2%左右的水平。与劳动和能源快速上升的效率变化趋势不同,资本的效率呈现出持续的下降趋势,年均增长率(AK)为-7.9%。资本效率的不断下降警示中国,依靠投资拉动经济增长难以持续。
那么,相关因素在要素效率的演进中具有怎样的实际影响呢?根据(8)式,我们将要素效率的年均变化率分解,从而考察各因素对要素效率变化的贡献,结果见于表4,而主要结论如下所示。

表4 要素效率年均变化率的分解
(1)在各要素的效率演进中起到最重要作用的均为自发效率变化。如表4所示,各要素的自发效率变化趋势具有明显差异:劳动和能源的自发效率分别以年均7.5%和3.2%的速度上升,而资本的自发效率以年均11.1%的速度下降。自发效率变化在资本、劳动和能源的效率变化中分别占据了140.5%、44.9%和44.4%的份额。可见资本的效率下降完全来自于其自发效率的下降,而劳动和能源的效率提升在很大程度上得益于各自的自发效率增长。
(2)研发为资本效率的下降贡献了-17.7%,为能源效率的上升贡献了18.1%,意味着研发起到了制约资本效率下降以及提高能源效率的作用。虽然研发对劳动效率没有产生显著影响,但由于其对资本和能源的效率产生了较大的正面作用,因而加大研发力度还是能够有效地促进技术进步。研发没有显著地带来劳动效率的提高可能与中国的研发方向有关。
(3)出口对三种要素的效率均存在正面影响。出口带来的正面效应在一定程度上阻止了资本效率的下降(份额为-13.9%),也促进了劳动和能源的效率提升(份额分别为15.6%和20.8%)。出口的积极作用可能来自于企业加入出口市场获得的竞争与创新效应、规模经济效应、出口对象的知识溢出效应等。与出口带来要素效率的提升不同,进口对所有要素的效率均没有产生显著影响。进口溢出效应不明显的原因可能与中国的进口贸易结构有关,即中国的进口贸易品主要是大宗矿产和粮食等初级产品以及服务于加工贸易的进口零部件。
(4)FDI对资本效率具有正面作用,但作用较小,而其对劳动和能源的效率没有产生显著影响。与出口相比,FDI的正向溢出效应相对更弱,原因可能在于FDI的溢出效应具有两面性,其正向溢出效应在一定程度上被负向溢出效应所抵消了。虽然FDI为中国带来了先进的技术和管理经验,但是经营进程中追加技术投入的意愿不够强烈,反而会通过过度竞争、资源争夺甚至垄断等手段抑制本土企业的创新。
(5)人力资本在劳动效率增长中占了27.5%的份额,即人力资本的提升对劳动效率产生了显著的促进作用。改革开放以来,中国的教育事业得到了稳步发展,人口素质明显改善。特别是上世纪90年代末期高等教育的快速发展培养了大量高素质人才,对提高整体水平的劳动生产率起到了积极作用。基础设施对劳动效率和能源效率起到了积极作用,但对资本效率没有产生显著影响。基础设施的改善在劳动、能源的效率增长中的份额分别为12% 和16.7%,表明中国的生产率增长或技术进步在一定程度上受益于基础设施的改善。
3.技术变化的趋势与来源分析
不断上升的劳动效率和能源效率意味着这两种要素存在正向的要素增强型技术变化,而递减的资本效率则意味着资本存在负向的要素增强型技术变化。我们计算了各要素的技术变化率以及总的技术变化率。研究期间,中国技术变化率的年均值为4.3%,考虑到同期中国经济的实际增长率大约为10%,技术进步对中国经济增长的贡献约占四成。因此,我们的研究结果表明,虽然经济增长主要来自要素投入,但技术进步对经济增长也有显著的贡献。不过,需要警惕的是,研究期间,总的技术变化率呈现出逐步下降的趋势,从期初的4.8%下降到期末的3.7%。特别是从上世纪90年代后期开始,技术进步速度下降的趋势愈加明显,反映出经济增长质量的下滑。
要素特定的技术变化率具有较大的差异。劳动的技术变化率高达6.2%(2009年)至7.2%(1991年),超过了总的技术变化率。因此,劳动效率的提高,是中国技术进步的主要动力。不过,劳动的技术变化率呈现出下降趋势,也带动了总技术变化率的下降。能源的技术变化率在0.9%(1993年)至1.4%(2012年)之间,对总技术变化的贡献相对较小。但是,能源的技术变化率呈现出缓慢的上升趋势,对总技术变化的贡献因而也越来越大。资本的技术变化率为负,范围在-3.9%(1988年)至-3.3%(2008年)之间。因此,资本效率的下降在很大程度上抑制了中国的技术进步。
进一步地,我们考察技术变化的来源,即技术效应、价格效应和规模效应对技术变化的贡献。结果显示,总技术效应的范围在3.9%至5.2%之间,年均值为4.6%,超过了总技术变化率。总价格效应和总规模效应均为负值,范围分别在-0.7至-1.3%和-0.1%至-1.5%之间。从数值上看,总技术效应是总技术变化的主要贡献者,而其他两种效应对总技术变化的影响较小,且为负向影响。从变化趋势来看,总技术效应和总规模效应均呈现出下降的趋势,导致了总技术变化率的下降,而总价格效应表现为上升趋势,能够在一定程度上减缓总技术变化率的下降。
分要素来看,劳动的技术效应为正,范围在7.5%至9.1%之间,呈现下降趋势;资本的技术效应为负,范围在之间-3.6%至-4.1%之间,同样表现为下降趋势;而能源的技术效应在-0.2%至0.5%之间,在1985 ~1995年期间为负,之后为正,表现为上升趋势。
在要素特定的价格效应方面,资本和能源的价格效应均为正,范围分别在0.8%至1.1%,以及1.6%至1.8%之间,而劳动的价格效应为负,范围在-3.4%至-4.0%之间。显然,劳动的价格效应为负是导致总价格效应为负的唯一原因。因此,三种要素间相对价格的变化有利于资本和能源的技术进步,而不利于劳动的技术进步。特别是对于能源来说,其价格效应超过了能源的技术变化率,是能源增强型技术进步的主要原因。劳动的价格效应之所以为负,原因可能在于劳动与资本、能源的相对价格上升了。当一种要素(劳动)变得相对昂贵,为了节约成本,企业的理性选择是开发使用相对便宜的要素(资本和能源)的技术。
在要素特定的规模效应方面,三种要素的规模效应非常小。其中,劳动的规模效应在0.16%至0.26%的范围内,呈现微弱的上升趋势,而资本和能源的规模效应均在-0.6%至-0.9%的范围内,呈现微弱的下降趋势。可见,产出规模的扩张对劳动的技术变化产生了正向影响,对资本和能源的技术变化产生了负面影响。不过,无论是哪种影响,程度都较小。
四、结 论
本文放弃中性技术变化的假设,采用要素增强型技术变化模型,对要素效率因子进而技术变化采取了内生化设定,考察了1985~2012年期间中国资本、劳动和能源三种要素的效率变化趋势,以及各要素的效率变化在总技术变化中的作用。主要结论如下:
第一,三种要素的效率变化趋势具有显著差异。研究期间,劳动效率和能源效率持续上升,年均增长率分别为16.7%和7.5%,而资本效率表现出持续的下降趋势,年均下降7.9%。因此,劳动效率和能源效率的持续上升对改善中国经济增长的质量和绩效发挥了积极作用,而且还有助于缓解劳动力数量下降和不断趋紧的能源约束带来的压力,不过,资本效率的持续下降意味着投资驱动的经济增长模式面临着越来越大的挑战。
第二,同一经济因素在不同要素效率变化中的作用可能不同。具体而言:自发效率的变化在各要素的效率演进均起到了最重要作用;研发对劳动效率没有产生显著影响,但对资本和能源的效率产生了较大的促进作用;出口对三种要素的效率均起到了正面影响,但进口对所有要素的效率均没有产生显著影响;FDI除了对资本效率具有较小的正面作用外,对劳动和能源的效率均未产生显著影响;人力资本的提升显著地促进了劳动效率的提高,但对资本和能源的效率没有显著影响;基础设施对劳动效率和能源效率起到了积极作用,但对资本效率没有产生显著影响。
第三,研究期间,总的技术变化率年均值为4.3%,约占同期中国经济增长率的四成,表明技术进步在中国经济增长中发挥了非常重要的作用。不过,上世纪90年代后期技术进步的速度开始出现明显的下降趋势,反映出这段时期经济增长质量的下降。三种要素的技术变化对总技术变化的作用具有明显差异。劳动的技术变化率超过了总的技术变化率,表明劳动效率的提高是技术进步的主要动力。能源的技术变化对总技术变化的贡献相对较小,但随着能源的技术变化率的上升,其对总技术变化的贡献也将增加。由于资本效率的持续下降,资本的技术变化率为负,成为了技术进步的抑制因素。
第四,对技术变化的分解结果显示,技术效应是资本负向技术变化和劳动增强型技术变化的主要来源,但对能源增强型技术变化的影响较小。价格效应是能源增强型技术进步的主要原因,也在一定程度上有利于抑制资本的负向技术变化,但对劳动增强型的技术变化具有负面作用。规模效应对劳动增强型的技术变化产生了正向影响,对资本和能源的技术变化产生了负面影响。不过,无论是哪种影响,程度都较小。
注 释
①固定资本形成隐含平减指数=固定资本形成总额(当年现价)/(固定资本形成总额(上年现价)*固定资本形成总额发展速度(以上年为1)。
[1]Islam N,Dai E,Sakamoto H.Role of TFP in China's Growth[J].Asian Economic Journal.2006,20(2).
[2]戴天仕,徐现祥.中国的技术进步方向[J].世界经济.2010,(11).
[3]雷钦礼.偏向性技术进步的测算与分析[J].统计研究.2013,(04).
[4]Kumbhakar S C.Decomposition of technical Change into Input-specific Components:A Factor Augmenting Approach[J].Japan and the World Economy.2002,14(3).
[5]Christopoulos D K,et.al.Allocative Inefficiency and the Capital-Energy Controversy[J].Energy Economics.2002,24(4).
[6]张军,吴桂英,张吉鹏.中国省际物质资本存量估算:1952—2000[J].经济研究.2004,(10).
[7]Hall R E,Jones C I.Why Do Some Countries Produce So Much More Output Per Worker Than Others?[J].The Quarterly Journal of Economics.1999,114(1).
[8]陶小马,邢建武,黄鑫,等.中国工业部门的能源价格扭曲与要素替代研究[J].数量经济技术经济研究.2009,(11).
[9]Hu A G Z,Jefferson G H,Qian J.R&D and Technology Transfer:Firm-Level Evidence from Chinese Industry[J].Review of E-conomics and Statistics.2005,87(4).
[10]吴延兵.自主研发、技术引进与生产率——基于中国地区工业的实证研究[J].经济研究.2008,(08).
责任编辑:黎贵才
2014-09-23
定稿日期:2015-01-10
国家自然科学基金项目(71203018);教育部人文社会科学基金(12YJC790248)
袁鹏(1981-),男,四川荣县人,经济学博士,西南财经大学工商管理学院副教授,主要从事技术创新与产业发展研究;叶鑫(1989-),男,辽宁葫芦岛人,大连理工大学管理与经济学部硕士研究生,主要从事金融创新研究。
FF061.2
A
1005-2674(2015)03-067-07
