提升管内细长颗粒流化运动的气固多向耦合模型的构建
2015-08-22蔡杰钟文琪袁竹林
蔡杰,钟文琪,袁竹林
(1东南大学能源与环境学院,江苏 南京 210096;2南京师范大学能源与机械工程学院,江苏 南京 210042)
引言
细长颗粒的循环流化在工业生产中具有广泛的应用背景,如生物质秸秆在循环流化床中的燃烧、烟丝在循环流化床中的干燥或加湿、药丸在流化床内的干燥成型等[1-3]。因此,研究细长颗粒的循环流化特性具有重要的意义。相比球形颗粒的三自由度,细长颗粒具有六自由度,包括位置矢量和姿态矢量。由刚体动力学理论可知,刚体的姿态矢量用一组欧拉角(进动角、章动角和自转角) 唯一表示。细长颗粒的气固两相流模型研究主要着眼于细长颗粒的受力、运动(平动与转动)模型的构建,细长颗粒间的碰撞模型构建以及细长颗粒与流场之间耦合关系的构建等。而其运动研究则主要着眼于细长颗粒在沉降、上升或运动过程中的取向分布、浓度分布、旋转速度及位移等特征。细长颗粒的气固两相流研究主要采用欧拉-拉格朗日方法,流场作为连续相,采用欧拉方法处理,而细长颗粒则作为离散相,采用拉格朗日方法追踪其受力、运动及碰撞[4-7]。在早期阶段,细长颗粒与流场之间都是单向耦合,即仅考虑流场对细长颗粒的曳力,而不考虑细长颗粒的存在对流场特征的影响[4]。但事实上,即使是稀相流,细长颗粒的存在也会对流场产生较大的影响,因此,构建细长颗粒与流场[尤其是高Reynolds数(Re)湍流]之间的双向耦合关系具有极其重要的意义[8-10]。拉格朗日时间尺度与湍动能(κ)-湍流耗散率(ε)的关系的建立,为固粒相-流场双向耦合模型的构建奠定了基础[11]。近年来,时均Navier(N)- Stokes(S)方程直接模拟方法被应用于球形固粒在湍流流场中的扩散研究[12-13],但却几乎未见被应用于细长颗粒在湍流场中的扩散研究[14-15]。本文在文献[16]的基础上,通过引入拉格朗日时间尺度与κ-ε的关系,构建细长颗粒-湍流之间的双向耦合关系,并改进细长颗粒间碰碰模型,从而构建起高Re条件下细长颗粒-湍流多向耦合模型。并且,采用此模型对某提升管内的细长颗粒-湍流气固两相流场进行了数值模拟研究。
1 数学模型的构建
1.1 数学模型建立
本文将刚体动力学理论与经典的球形粒子气固两相流双向耦合模型结合,建立细长颗粒与气相场间的双向耦合关系。基于勒让德-高斯积分法将细长颗粒沿轴向离散成数个离散分段;独立计算各离散分段在流场中所受的曳力,同时记录该曳力的负值及该离散分段的体积;矢量合成各离散分段所受的曳力从而得到细长颗粒所受的合曳力,同时计算细长颗粒所受的力矩;根据欧拉动力学方程,计算细长颗粒的平动及转动。同时,对于每个流场网格,根据所有颗粒离散分段所占的体积份额获得网格中流场的空隙率,矢量合成网格内所有离散分段对其施加的反作用力作为时均N-S方程的受力源项;再基于κ-ε模型耦合关联式,分别计算κ方程及ε方程中的源项。从而构建起细长颗粒与流场之间的双向耦合关系。
1.1.1 流场数学模型连续方程
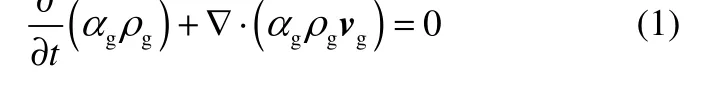
式中,αg为空气空隙率;ρg为空气的密度,kg·m-3;vg为空气的速度,m·s-1。
时均N-S方程

式中,vsi为细长颗粒离散分段的速度,m·s-1;m为流场网格中细长颗粒离散分段的数量;μ、μt分别为空气的黏度系数和湍流黏度系数,Pa·s;Ksg为气相场与细长颗粒离散分段之间的动量交换系数[17],此处采用Wen等[18]提出的经验关联式。
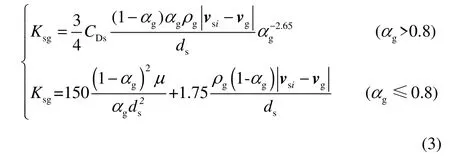
式中,CDs为细长颗粒离散分段的曳力系数,kg·s-1;ds为离散分段i的体积等效直径,m。由于是非球形颗粒,本文采用Sabine 等[19]提出的非规则颗粒曳力系数计算方法确定细长颗粒离散分段的曳力系数。

式中,dA为不规则颗粒的表面积等效直径,m;c为不规则颗粒的表面球形度;Res为Reynolds数;ρs为细长颗粒离散分段的密度,kg·m-3。
μt由式(5)计算

湍动能方程
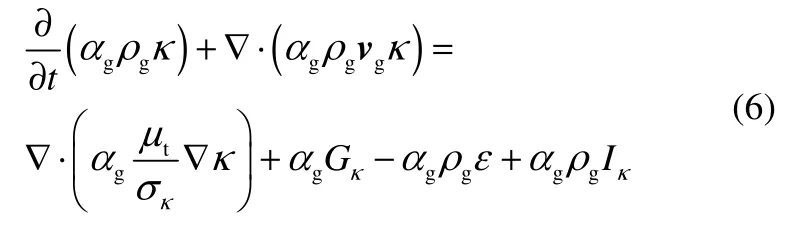
湍流耗散率方程

这里Gκ为湍动能的产生项,其意义与单相流体κ-ε模型中的意义相同;Iκ和Iε代表了固体相(s)对气体相(g)的影响。Elgobashi[20]提出Iκ和Iε可采用如下形式

这里ksg是气体相(g)、固体相(s)的速度的协方差,Simonin等[21]提出采用式(10)计算

其中,b由式(11)计算

式中,CV=0.5,为附加质量系数;ηsg则由式(12)计算

式中,τt为载能紊流涡的特征时间,定义如下

这里θ是细长颗粒离散分段平均速度和平均相对速度的夹角。

式中,Lt为紊流涡的长度标尺,定义为

τF,sg定义如下

这里σκ=1,σε=1.3,C1ε=1.44,C2ε=1.92,C3ε=1.2,Cμ=0.09,均为经验常数。该湍流源项模型能够很好地满足流场计算的稳定性要求。
1.1.2 离散相数学模型文献[16]中对细长颗粒沿长度方向离散采用均分数段的方法,但这样处理从数学上来讲具有不合理性,会导致一定程度的误差。因此,本文对之前的模型进行了改进,基于勒让德-高斯积分法,沿长度方向对细长颗粒进行数值离散。
模型中考虑到的力有气流对细长颗粒的曳力f和重力mg。细长颗粒在流场中所受的力为细长颗粒长度方向上各点受力的积分。细长颗粒在流场中的曳力f及定坐标系力矩Mf为

式中,l为细长颗粒的长度,m;f(x)是细长颗粒长度方向上各点所受的流体曳力,N·m-1;F(s)是(-1,1)区间单位长度所受的流体曳力,N·m-1;x=[-l+l+(l+l)s]/4。根据勒让德-高斯积分法,式(19)相应的求积公式为

其中,n=10为细长颗粒离散分段的数量;λi为高斯求积系数;Fi(si)为每个离散分段所受的流体曳力,N·m-1;li为每个离散分段的长度,m;r(si)为定坐标系中细长颗粒离散分段相对于细长颗粒质心位置的单位矢量,m。
Fi(si) 的计算公式为

每个离散分段的速度为

其中,vs0为细长颗粒的质心速度,m·s-1;I为由动坐标系向定坐标系转换的余弦矩阵;ω为细长颗粒在动坐标系中的角速度,rad·s-1。
细长颗粒的位移(平动)及转动方程见文献[16]。
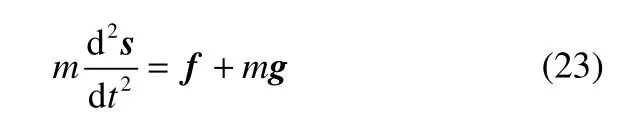
式中,s为细长颗粒的位移,m;m为细长颗粒的质量,kg;g为重力加速度,m·s-2。
本文在文献[16]基础上,对Nabu碰撞概率模型进行修正,从而建立基于细长颗粒离散分段的细长颗粒碰撞概率模型。其思路如下:对处于同一流体网格内的细长颗粒离散分段进行排序,并根据Nabu碰撞概率模型逐一判断每个细长颗粒离散分段将会与其他哪个细长颗粒离散分段发生碰撞(同一细长颗粒不同离散分段之间的碰撞被排除),则其所归属的两个细长颗粒将会发生碰撞,并且这两个细长颗粒离散分段即为细长颗粒间碰撞的碰点。该处理方式无须额外再构建一套网格。在进行网格尺度确定时需要考虑两方面的因素:一是同一细长颗粒上不同离散分段受力的差异;二是同一网格内不同细长颗粒离散分段碰撞。因此,本文在定义网格尺寸时,以最长细长颗粒长度的1/2作为网格尺寸。
离散分段i和同一网格内其他细长颗粒离散分段的碰撞概率为

式中,n为真实颗粒数;N为取样颗粒数;Gij为细长颗粒分段i和j的相对速度,m·s-1;Δt为时间步长。
在细长颗粒离散分段i总碰撞概率Pi小于1时,利用随机数R(0
限于篇幅,对两细长颗粒间的刚性碰撞模型此处不做详细介绍,见文献[16]。
细长颗粒与壁面的处理采用壁面碰撞处理,壁面碰撞处理同样基于刚体碰撞理论,并将墙壁设为质量无穷大、速度为零的刚体,具体模型可见文献[22]。
1.1.3 模型计算连续采用基于同位网格的SIMPLE方法计算。先进行单相连续相的计算,获得收敛解之后,开始细长颗粒受力、运动方程求解,细长颗粒的平动及转动轨迹的计算。细长颗粒相连续计算一定的时间步数后,在进行细长颗粒受力运动计算的同时,计算细长颗粒离散分段在连续相网格中所占的空隙率、连续相网格所受反作用力源项以及κ-ε模型中的源项,并代入连续相计算从而获得新的连续相。然后基于新的连续相继续进行颗粒场的计算,从而实现连续相和细长颗粒相连续交替耦合求解。本文中设定的时间步数间隔为10个时间步,即每10个时间步重新更新连续相。图1为计算流程。
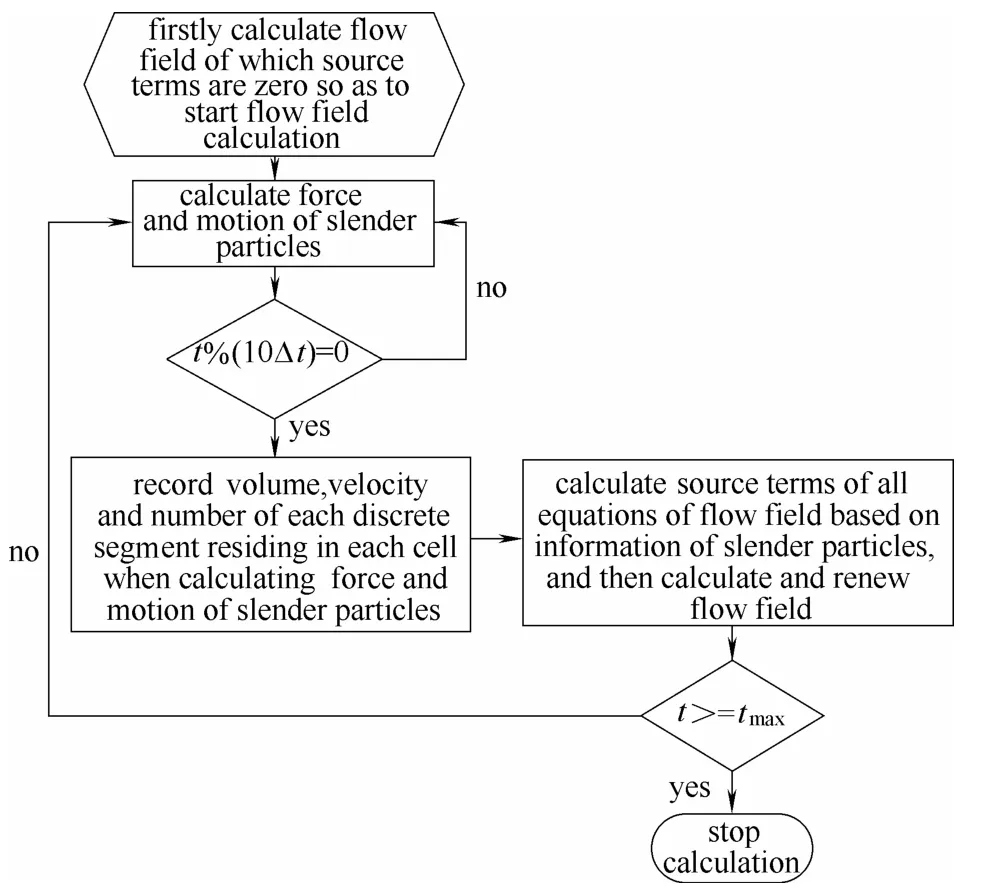
图1 程序计算流程 Fig.1 Computational flow chart of program
连续相-细长颗粒相双向耦合两相流程序全部由c++实现。采用Dell precision T5610工作站(内存128G 双E5-2637处理器)进行计算。由于完成连续相的迭代计算和细长颗粒的碰撞判断及计算均需较长时间,因此完成一个算例需超过10 d时间。
1.2 数值模拟参数及条件
本文数值模拟对象为一矩形提升管内的细长颗粒气-固两相流场,提升管的长宽高为0.5 m×0.5 m×3 m,采用的实验细长颗粒为密度、外形均匀性良好的秸秆(火柴棒)。为最大程度还原加料环境,细长颗粒初始速度为0,角速度在动坐标系3个轴上投影为0~2 rad·s-1,3个欧拉角为0~π,以上均以随机方式给出。每隔0.01 s,从提升管入口处放入一定数量的细长颗粒,本文中采用了4种长径比的细长颗粒,并按一定级配由床层底部放入。实际的工作条件如表1所示。典型的计算区域如表2所示。

表1 实际的工作条件 Table 1 Actual conditions

表2 典型的计算区域 Table 2 Typical calculation regions
2 数值模拟结果与分析
2.1 细长颗粒流化数值模拟图
受目前实验技术能力与条件的限制,当前细长颗粒的流化运动实验主要依靠高速摄像抓拍一些细长颗粒在流化运动过程中的浓度分布特性。数值实验中,当细长颗粒到达提升管出口之后,提升管内细长颗粒的数量基本保持在10000个左右,相较实验的颗粒量多,因此实验照片与数值模拟图略有差异。图2和图3分别按一定百分比配比的4种不同长径比的细长颗粒物料在不同时刻的流化模拟图和实验照片。由图2可以明显看出,细长颗粒在上升运动过程中伴随着强烈的旋转,这与实验照片结果吻合。尽管实验颗粒量相对于模拟颗粒量较少,但是从实验图中可以明显看出细长颗粒在流化运动过程中存在絮团现象,在不同时刻不同区域细长颗粒数量浓度明显差异,这说明即便细长颗粒的数量浓度较低,数值建模也需考虑细长颗粒间的相互作用。在流化运动过程中,会有一些细长颗粒脱离颗粒群,以较高的速度向上运动,这在数值模拟图与实验照片中均有明显的体现。这说明本文所建模型是合理的。

图2 提升管内不同时刻细长颗粒流化 运动模拟图(5 m·s-1) Fig.2 Simulation of fluidization of slender particles in riser at different time (5 m·s-1)

图3 提升管内不同时刻的细长颗粒流化 运动照片(5 m·s-1) Fig.3 Photos of fluidization of slender particles in riser at different time (5 m·s-1)
2.2 细长颗粒径向浓度分布
图4为提升管内沿水平中心轴线上由中心四周方向的细长颗粒的数量浓度分布。由图4可以看出,由中心向四周方向,细长颗粒的数量浓度由低到高逐渐增加,但到近壁处后又有明显的下降。细长颗粒数量浓度最低区域在中心区域,而数量浓度最高区域在靠近近壁处区域。这个结论与实验照片的定性结论(肉眼观测)是一致的,与球形颗粒在流化床提升管内的数量浓度分布规律也是一致的。这说明与球形颗粒流化运动过程一样,细长颗粒在提升管内上升运动过程中同样伴随着明显的水平迁移,由中心向四周移动。原因在于流场中心区域的径向速度大于四周区域的径向速度。并且,由于壁面的碰撞反弹等原因,细长颗粒最高数量浓度区域并非出现在近壁区,而是靠近近壁区区域。

图4 提升管内水平中心轴线上不同时间时的 细长颗粒浓度分布 Fig.4 Number concentration distribution of slender particles along horizontal center axis in riser at different time
2.3 流场内细长颗粒的取向分布
由于细长颗粒在流化运动过程中的向上运动速度非常快,因此通过实验手段获得其流化过程中的取向分布特性是非常困难的。本文采用了一种简化的办法,通过测量实验图片中的细长颗粒的长度,将实验图片中与拍摄平面接近平行的细长颗粒取出来,测量其与z轴的夹角,从而获取细长颗粒在流化运动过程中的取向分布特性。图5显示了整个提升管内细长颗粒的取向分布的数值模拟与实验结果。从图5中可以看出,两者的结论大体是一致的。在流化运动过程中,大多数细长颗粒以其轴与流场主流速度方向呈较小的夹角向上运动。并且,以0°~15°夹角向上运动的细长颗粒数量最大。这是由于细长颗粒以对流场影响最小的形式(能量最小化)在流场内做流化运动。
2.4 流场内空隙率分布

图5 流场内细长颗粒的取向分布 Fig.5 Orientation distribution of slender particles in riser
受目前细长颗粒两相流实验技术能力的限制,通过实验手段获取流化过程中流场的速度、压强、空隙率等流场信息是非常困难的,而数值模拟却提供了获取这些流场信息的有效途径。图6反映了提升管内1.63 m和2.55 m高度,沿中心轴线方向上,0.48、0.51、0.54和0.57 s时刻的流场空隙率分布。从图6可以看出,由于是非稳态过程,因此不同时刻的空隙率差异非常明显。在1.63 m和2.55 m高度,沿中心轴线方向上,空隙率的分布非常不规则,但大体而言,中心区域的空隙率要大于四周其他区域,这与流化床内颗粒浓度分布特性基本对应,中心区域细长颗粒数量浓度低,四周区域的细长颗粒数量浓度高。空隙率最低的区域出现在中心区与近壁区之间的过渡区域,这说明该区域的细长颗粒的浓度最高。并且,在流化运动过程中,由于细长颗粒间的相互碰撞的影响,细长颗粒的浓度分布的随机性非常强,甚至某时刻某位置处,如图6所示,1.63 m高度上,0.51 s时刻及2.55 m高度上,0.48 s、0.51 s、0.54 s时刻,当地流场没有细长颗粒(离散分段)的存在,因而该处的流体空隙率均为100%。这些充分说明细长颗粒的迁移以及流场参数随时间变化过程中具有非常强的随机性。因此,采用非稳态模型模拟细长颗粒的流化运动是合理的。

图6 提升管内水平中心轴线上不同时刻的流体空隙率分布 Fig.6 Volume fraction distribution of local flow field along horizontal center axis in riser at different time
2.5 流场内静压强分布
图7反映了提升管内1.63 m和2.55 m高度,沿中心轴线方向上,0.48、0.51、0.54和0.57 s时刻的压强分布。从图7中可以看出,随着时间增加,流场的静压强总体呈逐渐下降趋势,这是由于随着时间的增加,流场内的细长颗粒的数量不断增加,流场需要将更多的能量传递给当地的细长颗粒。与图6 相对应,空隙率下降明显的区域,当地静压强相对其他地区有更加明显的突降,这也是由于当地流场需要传递更多的能量给处于当地流场的细长颗粒(离散分段),使它们获得足够的能够向上运动的能量,细长颗粒(离散分段)量越多,静压强突降越明显。在1.63 m高度上,0.51 s时刻及2.55 m高度,0.48、0.51、0.54 s时刻,由于没有细长颗粒停留在当地,因此沿轴线方向上静压强变化不明显。此外,由图7可以看出,沿该轴线方向上的当地流场的静压强值并不是一条水平线,而是有一定程度的上下波动。这是由于当地流场受到上下前后左右流场的影响,而轴线方向上的当地流场上下前后左右的流场是不一样的,因此,轴线上所有流场的静压强值并不是一条水平线。

图7 提升管内水平中心轴线上不同时刻的压强分布 Fig.7 Pressure distribution of local flow field along horizontal center axis in riser at different time
2.6 湍流速度的分布特征
图8显示了提升管内1.63 m和2.55 m高度,沿中心轴线方向上,0.48、0.51、0.54和0.57 s时刻的当地湍流速度分布。从图8中可以看出,湍流场速度分布大体呈中间水平,近壁处迅速下降趋势。流场中间区域的速度梯度较小是由于湍流的扰动作用,而近壁处则由于层流黏性支层的影响,速度值迅速下降,直至与壁面速度相同。并且,在有细长颗粒停留的流场区域,流场速度值会有突降,这部分突降的速度值被转移给细长颗粒(离散分段),以使它们获得向上运动的能量。当地流场停留的细长颗粒(离散分段)量越多,当地流场的空隙率越小,速度值下降也越明显。由于每个流场网格的流场参数变化会受到上下前后左右流场的影响,而轴线方向上的当地流场上下前后左右的流场是不一样的,此图上沿轴线方向的速度值并不是严格的水平线,而是有一定程度的上下波动。

图8 提升管内水平中心轴线上不同时刻的湍流速度分布 Fig.8 Turbulent velocity distribution of local flow field along horizontal center axis in riser at different time
3 结论
本文针对当前高Reynolds数条件下细长颗粒气固两相流模型发展尚不完善的现实情况,基于κ-ε模型的球形粒子-流场气固间耦合关联式,构建了细长颗粒-湍流场气固双向耦合模型,并采用该气固双向耦合模型对细长颗粒气固两相流场进行了数值模拟研究。研究发现,在此提升管内,细长颗粒气固两相流场有以下几个特点。
(1)细长颗粒在提升管内向上运动过程中伴随有较明显的水平迁移,由中心向四周区域迁移,但细长颗粒数量浓度最大区域并不是近壁区,而是靠近近壁区区域。
(2)细长颗粒在流化运动过程中具有非常明显的取向选择性,细长颗粒多数以其轴趋于与主流速度平行的运动姿态向上运动。
(3)沿水平轴线方向上,流场四周区域的空隙率小于中心区域的空隙率,并且空隙率分布具有较强的随机性。
(4)随着提升管内颗粒数量的大量增加,当地流场的静压强会有明显的下降,并且,空隙率越小的区域,当地静压强会有突降。
(5)湍流场速度沿径向呈中间均匀,而近壁处则由于黏性支层的原因而急速下降直至与壁面速度相同分布,并且,有细长颗粒(离散分段)停留的区域当地速度会有较为明显的下降。
[1] Bernstein O, Shapiro M.Direct determination of the orientation distribution function of cylindrical particles immersed in laminar and turbulent shear flows [j].Journal of Aerosol Science, 1994, 25(1): 113-136.
[2] Lin Jianzhong, Lin Jiang, Shi Xing.Research on the effect of cylinder particles on the turbulent properties in particulate flows [J].Applied Mathematics and Mechanics, 2002, 23(5): 483-488.
[3] Lin Jianzhong(林建忠), Wang Changbin(王常斌), Shi Xing(石兴).Effects of wall on the sedimentation of cylindrical particles in the Newtonian fluid [J].Chinese Journal of Applied Mathematics(应用力学学报), 2003, 20(4): 1-6.
[4] Hilton J E, Mason L R, Cleary P W.Dynamics of gas-solid fluidised beds with non-spherical particle geometry [J].Chemical Engineering Science, 2010, 65(5): 1584-1594.
[5] Yin C, Rosendahl L, Kær K, et al.Modelling the motion of cylindrical particles in a nonuniform flow [J].Chemical Engineering Science, 2003, 58(15): 3489-3498.
[6] Fan L, Mao Z S, Wang Y D.Numerical simulation of turbulent solid-liquid two-phase flow and orientation of slender particles in a stirred tank [J].Chemical Engineering Science, 2005, 60(24): 7045-7056.
[7] Wang Yelong.Numerical study on sedimentation of mutual-collision cylindrical particles in the vertical channel [J].Applied Mathematics and Mechanic, 2006, 27(7): 859-866.
[8] Gore R, Crowe C.Effect of particle size on modulating turbulent intensity [J].Int.J.Multiphase Flow, 1989, 15: 279-288.
[9] Paschkewitz J S, Dubief Y, Dimitropoulos C D, et al.Numerical simulation of turbulent drag reduction using rigid fibres [J].J.Fluid Mech., 2004, 518: 281-317.
[10] Zhang Weifeng, Lin Jianzhong.Research on the motion of particles in the turbulent pipe flow of fiber suspensions [J].Applied Mathematics and Mechanics, 2004, 25(7): 677-685.
[11] Shuen J, Chen L, Faeth G.Evaluation of a stochastic model of particle dispersion in a turbulent round jet [J].AIChE J., 1983, 29(1): 167-170.
[12] Matteo C, Mathiesen V.Numerical simulation of particulate flow by the Eulerian-Lagrangian and the Eulerian-Eulerian approach with application to a fluidized bed [J].Comput.Chem.Eng., 2005, 29(2): 291-304.
[13] Xiong Yuanquan(熊源泉), Yuan Zhunlin(袁竹林),Zhang Mingyao(章名耀).Three-dimensional numerical simulation on conveying properties of gas-solid injector under pressurization [J].Journal of Chemical Industry and Engineering (China) (化工学报), 2004, 55(10): 1638-1643.
[14] Lin Jianzhong, Lin Jiang, Shi Xing.Research on the effect of cylinder particles on the turbulent properties in particulate flows [J].Applied Mathematics and Mechanics, 2002, 23(5): 483-488.
[15] Qi D W.Simulations of fluidization of cylindrical multiparticles in a three-dimensional space [J].Int J.Multiphase Flow, 2001, 27(1): 107-118.
[16] Cai Jie(蔡杰), Fan Fengxian(凡凤仙), Wu Xuan(吴晅), et al.Effects of inter-particle collisions on the orientation distribution of slender particles in gas-solid flows [J].Proceedings of the CSEE(中国电机工程学报), 2008, 28(17): 66-69.
[17] Crowe C T, Troutt T R, Chung J N.Numerical models for two-phase turbulent flows [J].Annual Review of Fluid Mechanics, 1996, 28: 11-43.
[18] Wen C Y, Yu Y H.Mechanics of fluidization [J].Chem.Eng.Prog.Sump.Serie., 1966, 62: 100-113.
[19] Sabine T C, Michael G, Efstathios E M.Drag coefficients of irregularly shaped particles [J].Powder Technology, 2004, 139: 21-32.
[20] Elgobashi S.Particle-laden turbulent flows: direct simulation and closure models [J].Applied Scientific Research, 1991, 48: 301-314.
[21] Simonin O, Deutsch E, Miniter J P.Eulerian prediction of the fluid/particle correlated motion in turbulent two-phase flows [J].Applied Scientific Research, 1993, 51: 275-283.
[22] Cai Jie(蔡杰), Peng Zhengbiao(彭正标), Wu Xuan(吴晅), et al.Simulation study on the effects of wall on the fluidizing features of slender particles in gas-solid flows [J].Proceedings of the CSEE(中国电机工程学报), 2008, 28(23): 71-74.
