振动式密度分离筛筛分机理的数值仿真
2015-08-22史俊杰周自强戴国洪
史俊杰,周自强,戴国洪,3
(1.苏州大学 机电工程学院,江苏 苏州 215000;2.常熟理工学院 机械工程学院,江苏 常熟 215500;3.苏州市汽车绿色拆解回收利用智能装备技术重点实验室,江苏 常熟 215500)
振动式密度分离筛筛分机理的数值仿真
史俊杰1,周自强2,戴国洪2,3
(1.苏州大学 机电工程学院,江苏 苏州 215000;2.常熟理工学院 机械工程学院,江苏 常熟 215500;3.苏州市汽车绿色拆解回收利用智能装备技术重点实验室,江苏 常熟 215500)
为了对报废汽车破碎物料中的非金属物料进行机械分离,分析了破碎物料在筛面上抛掷和滑移过程的基本模型,得到了物料在筛面上的运动微分方程.用MATLAB对物料的运动进行了分析、编程和运算.基于运算所得数据和结果,对筛面上的物料运动轨迹进行了仿真输出,为密度分离筛的系统设计提供了理论依据.
报废汽车破碎物料;破碎物料的抛掷和滑移;数值仿真;密度分离筛
随着报废汽车数量的日益增多,报废汽车破碎物料回收利用逐渐被重视起来.报废汽车破碎物料混合物多以金属和橡胶塑料为主,可以利用分选技术将其分离回收.区别于涡流分选、磁力分选和光选等复杂的分选技术,振动分选是一种经济、高效、节能、环保的新技术.密度分离筛筛面通过电磁激振器顶杆的带动做周期性振动,筛面上的物料在振动作用下做往复运动.根据报废汽车破碎混合物料的不同弹性模量和动摩擦因数,建立混合物料中金属弹性物料抛掷和非金属塑性物料滑移的运动微分方程,并用MATLAB数值仿真出金属弹性物料和非金属塑性物料的位移、速度曲线,从而得到金属和非金属两种物料在密度分离筛筛面上不同的运动轨迹.
1 力学模型
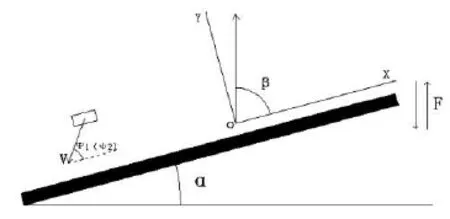
图1 单颗粒物料在振动筛面上的力学模型图
物料在筛面上的运动可分为上滑运动、下滑运动、上滑大于下滑运动、下滑大于上滑运动、抛起运动5种类型,适当地选择振动筛的运动学参数(振幅、振动方向角、筛面倾角和频率等),便可以让振动筛中的物料按上述的任意一种运动方式运动而实现分选物料.
假设颗粒无滑移,可建立如图1所示的表示振动筛与单颗粒物料之间的关系模型图,X轴与筛面平行向上,Y轴与筛面垂直向上.其中α为筛面倾角,β为振动方向线与筛面的夹角(振动方向角),φ1(φ2)为物料的抛始角(滑始角),破碎物料的质量为m,破碎物料的重力为G.振动筛在简谐振动力F的作用下与单颗粒物料发生碰撞[1].
直线振动筛的工作面沿振动方向线做简谐振动,由动力学分析可知,直线振动筛工作面的位移方程为[2]

式中A——振动筛单振幅;
w——振动筛的振动频率;
φ——振动相角(°).
将振动筛板的位移分解成x方向(平行于筛面向上)和y方向(垂直于筛面向上),便得x方向和y方向的位移

式中β——振动方向角(°).
求式(2)对时间t的一次导数和二次导数,便得x方向和y方向的速度vx和vy

2 物料的运动方程和MATLAB运动轨迹仿真

式中α——振动筛筛面倾角.
而沿y方向破碎物料作用于筛面上的正压力为

当破碎物料对筛面做滑行运动时,物料与筛面始终保持接触,正压力Fn≥0,相对加速度Δy..=0,当物料出现抛掷现象时,正压力Fn=0,相对加速度Δy..≠0,在物料与筛面接触的情况下,筛面和物料的极限摩擦力为

式中 fs——静摩擦因数.
物料滑动开始的瞬时,物料对筛面的相对加速度Δx..=0,因为物料此时没有抛掷运动,Δy..=0,所以式(5)的Ft和式(7)的F0之和等于零,即

将式(5)及式(7)代入式(8),并将式(6)及式(4)代入,即得
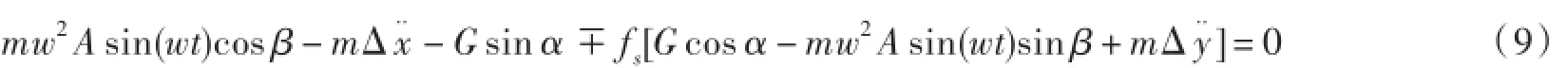
报废汽车破碎物料中含有两类主要物料:金属和非金属,因为这两类物料的动摩擦因数相差很大,所以以它们来说明破碎物料运动方程的计算和运动轨迹仿真的过程.
假设报废汽车破碎物料对筛面做相对运动,在x轴方向和y轴方向的相对位移为Δx、Δy;相对速度为Δx、Δy.则破碎物料沿x方向的惯性力和重力分力之和Ft为
因为 fs=tan μ(μ为动摩擦角),G=mg,代入式(9),并化简,可得正向滑行指数和反向滑行指数分别为
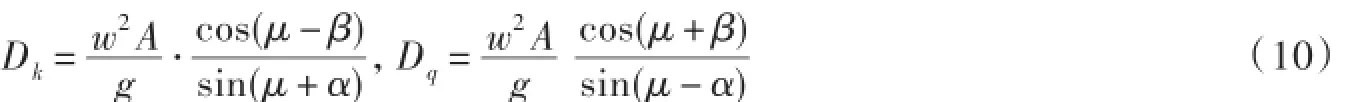
g——重力加速度.
当破碎物料做抛掷运动的瞬时,沿y方向的相对加速度Δy..=0,正压力Fn=0,由式(4)和式(6)得

式中φ1——弹性物料的抛始角.
由式(11)可以求出物料的抛掷指数D为

2.1金属弹性物料的运动方程和MATLAB运动轨迹仿真
金属破碎物料分为黑色金属和有色金属,其中以黑色金属为主,因为金属物料弹性模量大,且金属物料与不锈钢筛板之间的动摩擦因数小,当选取合适的物料抛始角后,物料的抛掷指数D≻1,金属物料只在筛板上做弹跳运动,此时金属物料在y轴方向的位移方程为

y轴方向的速度方程为

x轴方向的速度方程为

xD
式中φ——弹性物料的抛止角;
iD——抛离系数;
D——抛掷指数.
选取 φ1=55°,iD=0.37,D=1.22,a=10 mm,α=30°,β= 60°,w=40π,得到金属物料在y轴方向的位移、速度曲线和x轴方向的速度曲线如图2所示[3].
2.2非金属塑性物料的运动方程和MATLAB运动轨迹仿真
非金属破碎物料大多是塑性物料,且非金属物料与不锈钢筛板之间的动摩擦角都大于14°,所以与筛面产生碰撞后,物料只发生上滑运动或者上滑大于下滑运动.
当物料正向滑行指数Dk≻1,反向滑行指数Dq≺1时,物料只处在上滑运动状态,此时物料在x轴方向的位移方程为
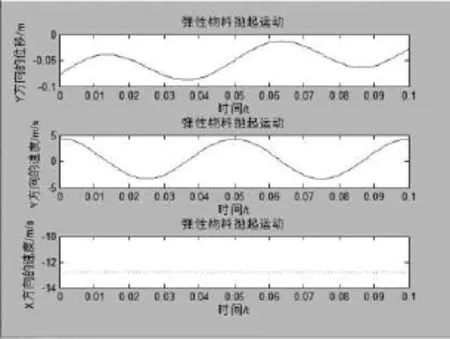
图2 金属弹性物料在y轴方向位移、速度曲线和x轴方向速度曲线

式中m=-[sin φ-sin φ2]+z⋅(φ2-φ22)/2-cos φ2(φ-φ2);
z=sin(α+μ)/k/cos(μ+β);
k=w2A/g;
φ2——物料滑始角;
φ——物料滑止角.
x轴方向的速度方程为

式中z1=sin(α+μ)/k/cos(μ+β).
选取 φ2=55°,四种动摩擦角不同的物料 μ1=15°,μ2=20°,μ3=25°,μ4=30°,a=10 mm,α=30°,β= 60°,w=40π,得出四种不同的非金属物料在x轴方向的位移和速度曲线如图3和4所示.
当物料正向滑行指数大于反向滑行指数时,即Dk≻Dq≻1时,物料只处在上滑运动大于下滑运动状态,此时物料x轴方向的总位移方程为
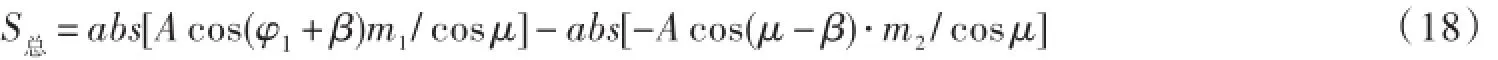
式中m1=-[sin φ-sin φ1]+sin(α+μ)/k/cos(μ+β)⋅(φ2-φ12)/2-cos φ1⋅(φ-φ1);

图3 四种非金属塑性物料在x轴方向的上滑位移曲线

图4 四种非金属塑性物料在x轴方向的上滑速度曲线
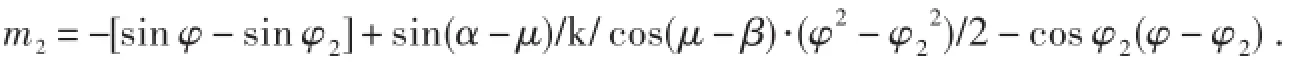
物料x轴方向的总速度方程为

式中

选取 φ2=55°,四种动摩擦角不同的物料 μ1=15°,μ2=20°,μ3=25°,μ4=30°,a=10 mm,α=30°,β= 60°,w=40π,得出四种不同的非金属物料在x轴方向的位移和速度曲线如图5和6所示.
由式(13)、式(14)、式(15)和图2可知:报废汽车破碎物料中的金属物料具有动摩擦因数小、弹性模量大的特点,在与筛面接触时发生弹性碰撞,产生反跳现象,因为从输送带给料时金属物料是在筛面法线上方,所以破碎金属物料是向筛面法线下方反跳,当金属物料再次落回筛面上时,其入料方向仍在筛面法线上方,因此其反跳方向必在筛面法线下方,即金属物料在做反向运动.
由式(16)、式(17)、式(18)、式(19)和图3、图4、图5、图6可知:报废汽车破碎物料中的非金属物料具有动摩擦因数大、弹性模量小的特点,在与筛面接触时发生塑性碰撞,因为塑性碰撞后弹跳很小,可以忽略不计,所以非金属物料直接在筛面上做滑移运动,当不同的非金属物料在筛面上滑移向上时,因为动摩擦因数不同,所以不同物料在筛板上可能直接做上滑运动或做上滑大于下滑运动.
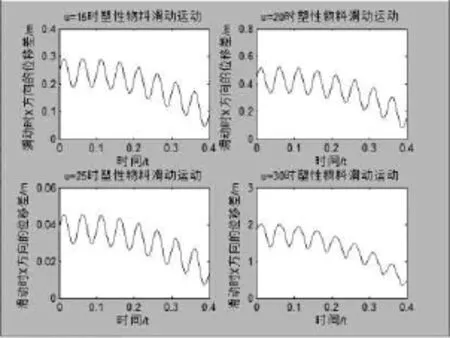
图5 四种非金属塑性物料在x轴方向的上滑大于下滑位移曲线

图6 四种非金属塑性物料在x轴方向的上滑大于下滑速度曲线
3 结论
通过理论分析得出物料在密度分离筛面上的运动微分方程和相关影响参数,通过参数改变可以有效地控制物料在筛面上的运动轨迹,选取合适参数后,通过MATLAB编程输出不同物料的位移、速度曲线,从而以这些参数为依据对密度分离筛进行系统设计.与传统小倾角筛板振动筛不同,振动式密度分离筛所选倾角较大,一般在25°~40°之间.尤其在筛面倾角等于30°时,非金属塑性物料的分选效果最佳.当选取合适的物料入料角后,报废汽车破碎物料中金属弹性物料在筛板上做向下抛掷运动,而非金属塑性物料在筛板上做向上滑移运动,这使非金属塑性物料能够通过密度分离筛振动分选出来.这种振动分选方法相对涡流分选、磁力分选和光选等复杂的分选技术[4-6],是一种原理简单、可实现性强、分选效率高的分选报废汽车破碎物料的技术,这为报废汽车破碎物料的有效分选提供了一种新技术.
[1]陆金新,刘初升.振动筛分过程中单颗粒的运动特性分析[J].煤矿机械,2007,28(11):66-68.
[2]闻邦椿,刘树英.现代振动筛分技术及设备设计[M].北京:冶金工业出版社,2013.
[3]丁毓峰.MATLAB从入门到精通[M].北京:化学工业出版社,2011.
[4]M·卢古.永磁立鼓式旋涡电流分选机[J].国外金属矿选矿,2002(7):37-40.
[5]张云雪.有色金属涡流分选机的特点与应用[J].再生资源与循环利用,2011,4(3):43-44.
[6]H·哈贝克.利用传感器拣选法分选含铝废料[J].国外金属矿选矿,2007(5):41-44.
Numerical Simulation for Principle and Mechanism of Density Vibration Screen
SHI Jun-jie1,ZHOU Zi-qiang2,DAI Guo-hong2,3
(1.School of Mechanical Engineering,Soochow University,Suzhou 215000,China;
2.School of Mechanical Engineering,Changshu Institute of Technology,Changshu 215500,China;
3.Key Laboratory of Intelligent Equipment for ELV Recycling Technology,Changshu 215500,China)
For the purpose of sorting shredder residue of body of end-of-life vehicle after disassembly,the basic model of throwing and sliding of scrap of residue is composed.And then,a differential equation is deduced.A numerical simulation is also established to calculate the motion of scrap on the screen surface.In the end,the result of simulation is discussed and some suggestions are put forward on the structural design of density screen.
shredder residue of body of end-of-life vehicle;throwing and sliding of scrap of residue;numerical simulation;density screen
TH237+.6
A
1008-2794(2015)02-0024-05
2015-01-06
通讯联系人:戴国洪,教授,工学博士,研究方向:数字化制造技术与装备,E-mail:dgh@cslg.cn.
