电动汽车电机制动防抱死模型研究

李其军，陈庆樟

（常熟理工学院 机械工程学院，江苏 常熟 215500）

电动汽车电机制动防抱死模型研究

李其军，陈庆樟

（常熟理工学院 机械工程学院，江苏 常熟 215500）

为解决电动汽车电机制动研究中仿真模型构建困难，建模方法复杂的问题.根据电机制动的运行机理，建立基于PWM全桥调制方式的永磁无刷直流电机电气制动模型，与电动汽车电气制动过程的动力学特性相结合，在Matlab/Simulink环境下建立了电动汽车电机制动仿真模型.系统采用模糊控制策略，通过占空比调节，控制电气制动电流，使滑移率保持在理想范围.仿真结果表明采用模糊控制策略能够可靠地实现电机制动防抱死的功能，系统模型运行平稳、反应灵敏.该模型可以用于电动汽车电机ABS不同控制策略的仿真研究，作为电动汽车制动动力学研究以及制动电气特性研究的基本模型.采用模块化设计方法，修改方便，避免了繁琐的建模工作，在电动汽车电机制动相关研究中具有较强的实用价值.

电气制动；模糊控制；占空比调节；防抱死；仿真分析

驱动电机不同象限下的运行特性决定了电机制动系统与传统机械制动的不同，再生制动功能是电机制动实现节能的重要途径.通过电机制动实现车辆防抱死制动（ABS）是保证电动汽车制动安全性、能量回收的有效方式，同时也降低了制动系统的复杂程度，实现电机制动完全取代传统液压防抱死制动.针对电动汽车制动系统研究时，现场实物实验不仅成本高还面临着开发周期漫长、实验结果无法预测的缺点，所以如何构建高效的基于电机防抱死制动的电动汽车制动模型，对于电动汽车制动控制系统领域研究具有重要意义［1］.

目前对永磁无刷直流电机控制系统建模仿真研究中，多是电机驱动模型的构建.纪志成、沈艳霞等人通过对永磁无刷直流电机数学模型的分析，基于Matlab提出了一种无刷直流电机系统仿真建模的新方法［2］；文献［3-4］也进行了类似的研究，构建了永磁无刷直流电机控制系统模型，但鲜少见到针对永磁无刷直流电机电气制动控制系统模型构建的研究.本文对永磁无刷直流电机电气制动及车辆制动过程进行数学分析，在Matlab/Simulink环境下建立基于模糊控制的永磁无刷直流电机电动汽车电气制动ABS仿真模型.采用模块化设计方法构建BLDC（永磁无刷直流电机）电气制动本体模型、PWM控制模块、车辆动力学模块、滑移率控制模块等.经过仿真分析证明模型的有效性，对电机制动相关研究具有较强的实用价值.

1　BLDC电气制动数学模型

永磁无刷直流电机定子电流为方波，电机反电动势为梯形波，并作出如下简化假设［2］：（1）不计磁路饱和、电机涡流损耗和磁滞损耗；（2）忽略定子电流的电枢反应；（3）定子绕组采用无中线Y形接法，三相定子绕组的自感、互感均为常数；（4）三相定子绕组中电阻RA=RB=RC，LA=LB=LC；（5）三相绕组为星形连接，且没有中线，其等效模型为ia+ib+ic=0.

根据图1的等效模型，以及上面的假设可得BLDC的三相电压平衡方程为：

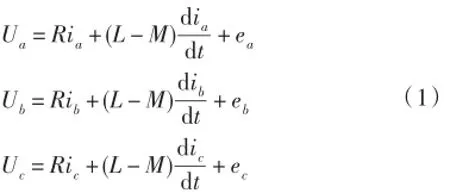
图1　永磁无刷直流电机等效模型

式中Ua,Ub,Uc为定子相绕组相电压（V）；R三相定子绕组电阻（Ω）；M为三相定子绕组之间的互感（H）；ia,ib,ic为三相定子相电流；ea,eb,ec为三相定子绕组反电动势.三相绕组中间点的电势：

永磁无刷直流电机的电磁转矩由电枢绕组与永磁体的电磁感应产生，根据能量守恒定律可知

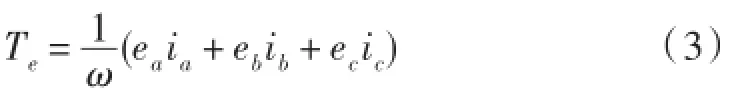
永磁无刷直流电机工作在电气制动状态时，一般采用两两导通的控制方式，定子电流为方波，反电动势为梯形波，反电势功率为负值，如图2所示.

在一个开关的调制周期内电气制动力矩也可以写为

其中E=ea=eb=ec，I=ia=ib=ic.

永磁无刷直流电电气机制动时的力矩平衡方程为

图2　定子绕组反电动势及电流

2　Matlab的制动系统模型建立

在Matlab 7.11/Simulink环境下，通过Simulink模块与SimPowerSystem模块的结合使用，在BLDC数学模型分析的基础上，提出了永磁无刷直流电机电动汽车的电气制动防抱死建模仿真方法，系统设计见图3.

图3所示滑移率控制模块对PWM生成模块施加控制，改变占空比D，控制逆变器功率管的开关，调节电机本体模块的电气制动转矩Te，Te作用于车辆动力学模块，改变车辆运行的速度和轮速.滑移率计算模块根据ω确定实时滑移率λ，与理想值λ*比较，反馈给滑移率控制模块，形成闭环跟随控制，可以实现电动汽车电气防抱死控制.

图3　电动汽车电气制动ABS建模框图

2.1电机本体模块

BLDC本体模块是电机制动模块中最重要的模块，电机本体模块根据输入的转子位置pos、转速ω，计算出电枢绕组反电动势ea,eb,ec，如图2所示.在BLDC本体建模中，反电动势的确定一直是较难解决的问题，目前常见的方法有：（1）有限元法［3］，这种方法建模得到反电动势脉动小，精度高，但是复杂，专业性强，不易推广.（2）傅立叶变换法［4］，该方法简单，但是需要进行大量三角函数值的计算，会降低仿真的运行速度.（3）分段线性法，分段线性法简单易行，且精度较高，能够较好地满足建模仿真的设计要求.本文在建模过程中采用分段函数法，如表1所示.输入量ua,ub,uc根据公式（1）计算得到相电流ia,ib,ic.

表1　转子位置和反电动势之间的线性关系

表1中Pos表示转子位置，ke为反电 动 势（V/（r/ min）），ω表示转速（rad/s），可以通过S函数编写或者查表模块实现反电动势模块的建模，本文中采用S函数的方式计算反电动势.

根据式（1）可以构建如图4所示电机本体模块.

2.2滑移率控制模块

滑移率控制模块中常用的控制策略有模糊控制、模糊PID控制以及变结构控制等，模糊控制策略不需要具体的数学模型，通用性较强.本文采用基于滑移率偏差e和偏差变化率ec为输入的模糊控制，输出为占空比增量dD，模糊规则设计如表2所示.

图4　电机本体模块BLDC

2.3转矩计算模块

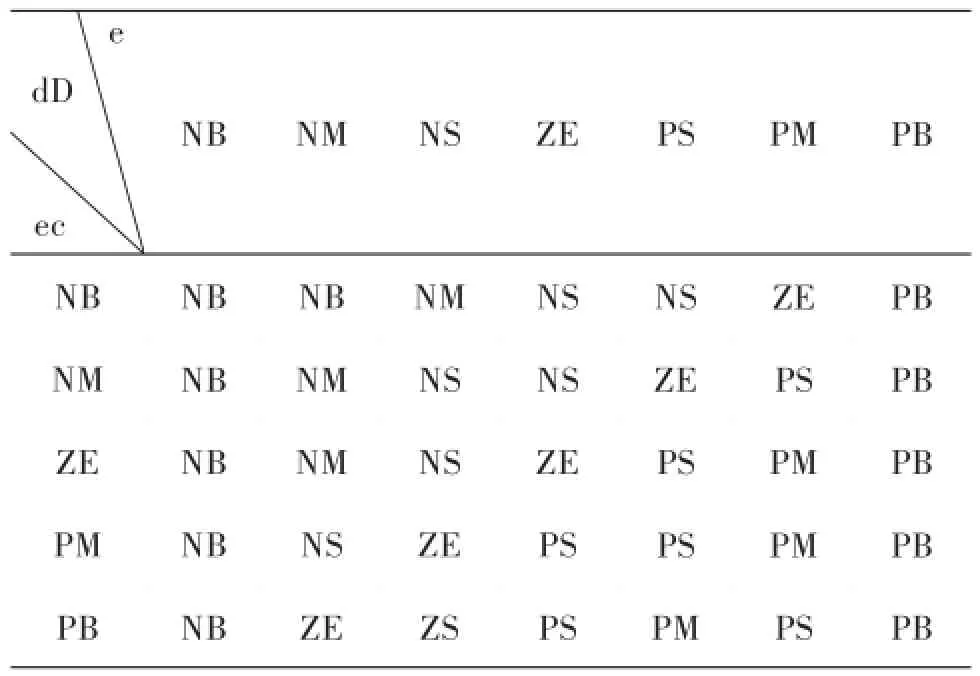
表2　模糊规则设计

由式（3）和（4）可以建立永磁无刷直流电机电气制动时的转矩计算模型，如图5所示.

2.4PWM信号生成模块

PWM信号生成模块中，采用占空比作为输入信号，设计中模糊控制器的输出为占空比增量dD，PWM信号生成模块根据占空比产生特定的逆变器控制信号PWM.目前研究中常见的PWM产生模型主要有电流滞环控制、使用SimPowerSystem中的 PWMGenerator模块、采用三角波比较控制等方式.三角波比较控制方式开关频率恒定，抑制了开关噪声的产生［5］，根据输入信号产生对应占空比的方波，输出信号直接输入逆变器模块，控制功率管的通断.改变三角波的发生频率产生不同要求的方波，灵活性较强，控制稳定，模型构建见图6.

图5　电气制动转矩计算模块

2.5逆变器模块

逆变器模块根据PWM信号以及转子的位置信号确定功率管开关的通断，产生要求的调节占空比，控制电机的端电压，控制电流，从而控制电气制动力矩.

分析位置信号Pos和端电压Ud之间的对应关系，利用S函数编程实现电压逆变器功能，模块的输入为位置信号Pos和PWM生成模块产生的控制信号PWM，输出为三相端电压信号，转子位置Pos和端电压U之间的关系如表3所示.

图6　PWM信号生成模块

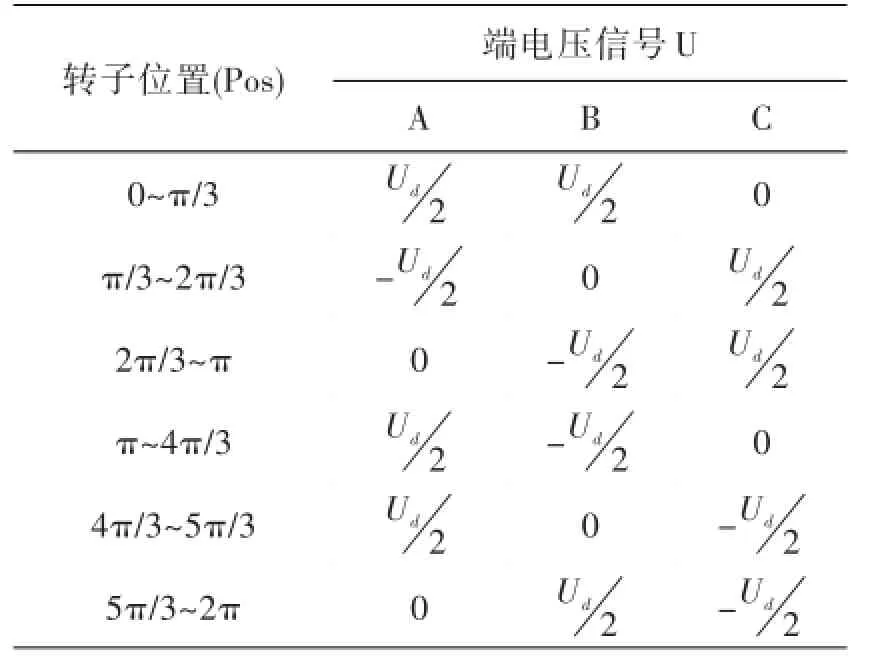
表3　位置信号和端电压之间的关系

3　车辆单轮模型

本文采用简化后的车辆单轮模型作为研究模型，该模型构建简单，只考虑主要的影响因素，同时又能够满足研究的需要.图7为单轮模型受力分析图，图中V为车轮中心前进的速度，即车速，Tb为电机通过传动系施加于车轮上的电气制动力矩，ω为车轮前进的角速度，Fs为制动时地面对车轮施加的纵向制动力，N为地面施加于轮胎的垂直方向的支持力，车辆制动过程中的受力分析及力矩平衡方程为：

根据式（6）～（9）可以搭建出如图8所示的速度-滑移率模型.研究中所建的车辆动力学模型主要包括：滑移率计算模块、车轮模型、车速计算模块以及轮速计算模块，仿真中的车轮模型采用魔术公式，输入滑移率输出为路面附着系数.

根据式（6）～（9）可以构建出如图8所示电动汽车动力学模型.

采用魔术公式构建轮胎模型，输入为车辆在制动时的实时滑移率λ，输出为路面附着系数 μ，图9为魔术公式模型产生的 μ λ之间关系.

将电动汽车单轮模型通过传动系统与永磁无刷直流电机电气制动模型相联接，可得如图10所示电动汽车电机制动ABS仿真结构图.

图7　车辆单轮模型

图8　速度滑移率计算模块

图9　滑移率-附着系数关系图

4　仿真结果

图10　电动汽车再生ABS模型结构图

本文仿真中相关参数的设计如表4所示.

仿真中，设置三角波的频率1000 HZ，仿真结果如图11～14所示.

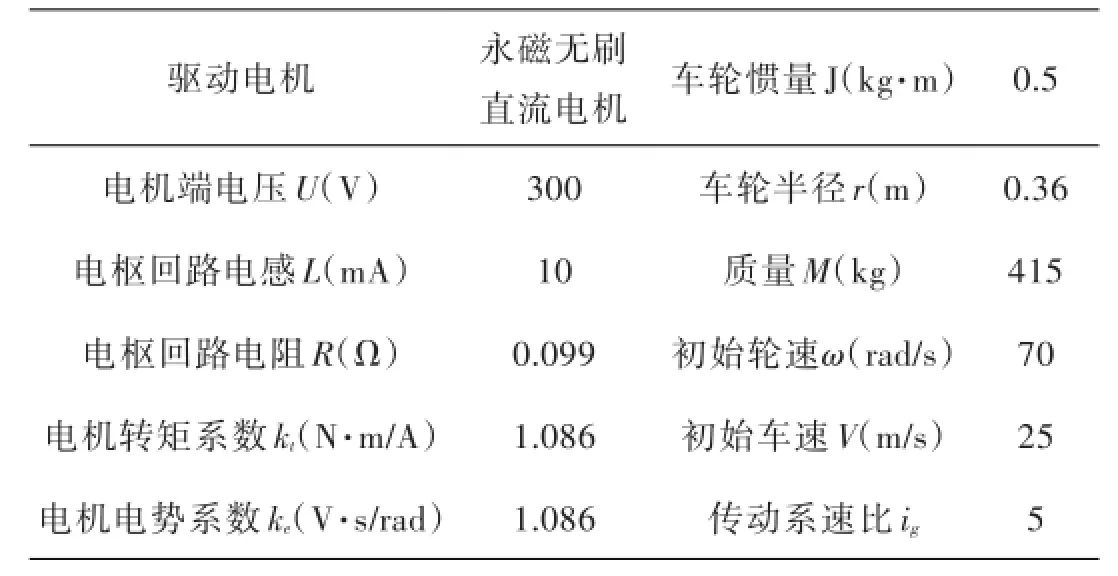
表4　仿真参数

从图11、图12的仿真波形可以看出，本文所采用的电动汽车仿真模型在制动期间滑移率保持在0.15～0.3之间波动，可以在较短的时间内停车，满足电动汽车防抱死制动强度的要求.图13反映了占空比调节情况，从图可以看出制动开始阶段占空比几乎全为最大值1（0=＜D＜=1），使轮速在短时间内快速下降；制动末期轮速降低至电机基速以下后无法采用回馈制动与反接制动交替的形式，反接制动提供所需的电机制动力矩占空比也为最大值1；在整个制动过程的大部分时间里占空比在［0，1］之间变化，永磁无刷直流电机处于回馈制动与反接制动交替的工作状态.

由仿真结果曲线可知设计中采用的控制策略可以通过调节占空比实现制动过程中的增力、减力和保侍，实现防抱死功能.

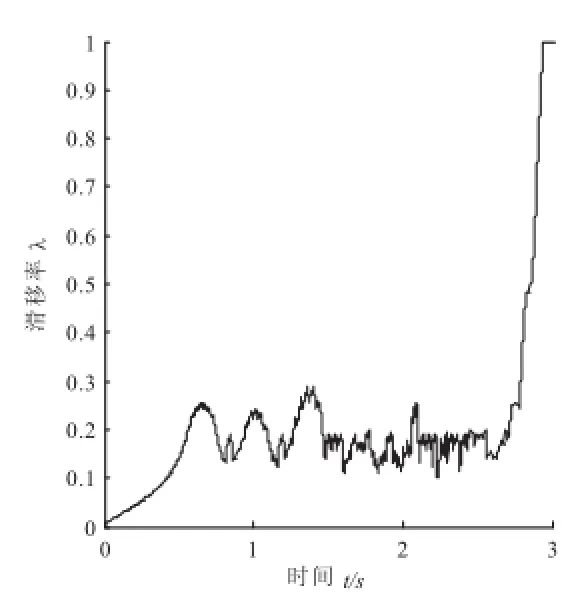
图12　滑移率变化曲线

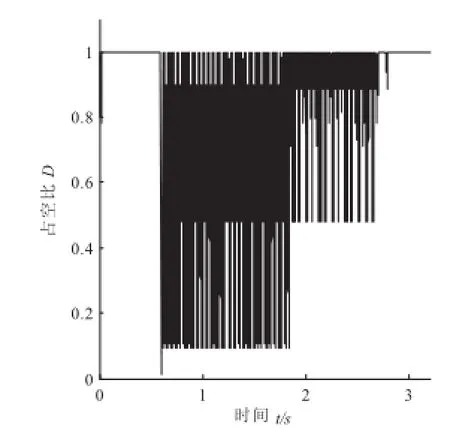
图13　占空比变化曲线

5　结论

本文在分析永磁无刷直流电机制动机理的基础上，建立了防抱死制动数学模型，结合电动汽车制动动力学原理，在Matlab/Simulink环境下，建立了电动汽车电机再生ABS模型，实现了电机制动在保证制动稳定性的同时进行制动能量回收，系统采用基于滑移率偏差e，偏差变化率ec的模糊控制方法，对模型进行了测试，仿真结果表明：通过模糊控制策略设计，系统模型能够平稳运行，具有较好的静、动态特性，反应灵敏.采用该模型可以便捷地实现验证控制算法，只需要对部分模块进行简单的修改和替换就可以实现不同的功能.同时该模型避免了一些简化模型忽略电机运行机理的缺陷，关注了动力学特点和电特性，只需要少量修改就可以同时作为电动汽车的动力学研究模型和运行时的电特性研究模型，各模块具有较强的通用性.因此它为设计和研究电动汽车电气制动控制系统提供了有效的手段和工具，为控制策略的研究提供了便利的仿真测试方法.

图14　电气制动力矩曲线

［1］Pragasan Pillay,Krishnan R.Modeling of per-manent magnet motor Drives［J］.IEEE Trans onIndustry Electronic,1988,35（4）: 537-541.

［2］纪志成，沈艳霞，姜建国.基于Matlab无刷直流电机系统仿真建模的新方法［J］.系统仿真学报，2003，15（12）.

［3］Ionel D M,Eastham J F,Betzer T.Finite el-ement analysis of a novel brushless DC mot-or with flux baeeiers［J］.IEEE Trans On Mg-netics,1995,31（6）:3749-3751.

［4］Jeon Y S,Mok H S,Choe G H,et at.A new simulation model of BLDC motor with r-eal back EMF waveform［C］.Proceeding from⁃Computers in Power Electronics,2000.USA,2000:217-220.

［5］黄俊，王兆安.电力电子变流技术［M］.北京：机械工业出版社，2000.

A Research on the Modeling of Anti-lock Braking of Motor in Electric Vehicle

LI Qi-jun，CHEN Qing-zhang
（School of Mechanical Engineering,Changshu Institute of Technology,Changshu 215500,China）

By analyzing the operation mechanism of Brushless DC motor（BLDC）,the electric braking mathemati⁃cal model of BLDC with full bridge modulation was set up,and in combination with vehicle dynamic characteris⁃tics during electric braking,the simulation model of electric braking of electric vehicle was established in Matlab/ Simulink so that the difficulties in building simulation model and complex modeling method in motor braking of electric vehicle could be overcome.Fuzzy control strategy was adopted in the system,and the braking current was controlled by adjusting the duty cycle to keep the slip rate in the ideal range.The simulation results show that the ABS based on motor braking can be realized by adopting fuzzy control strategy,and that the system is stable,with better static and dynamic characteristics.This model can be used in the researches on simulation of different control strategies for ABS in electric vehicle,and it can be used in the study on the electric vehicle dy⁃namics and electrical characteristics during braking.The modular design method is adopted.The model is easy to modify,avoiding the complicated modeling work,and it has a strong practical value in the researches related to motor braking in electric vehicle.

electric braking；fuzzy control；duty cycle adjusting；ABS；simulation analysis

U469.72

A

1008-2794（2015）02-0018-06

2014-12-16

苏州市科技计划工业应用基础指导项目（SGZ2014019）；常熟市科技计划工业基础项目（CQ201407）

通讯联系人：李其军，硕士研究生，研究方向：汽车机电一体化，E-mail：liqijun_cumt@163.com.