混凝土湿度场反演算法对比分析

□冯晓波(南水北调工程建设监管中心)

0 引言

混凝土水分减少导致干缩开裂，相关研究已开展较多，牛焱洲[1]采用有限元法，根据混凝土Fick扩散定律，求出自由干缩应力和湿度分布，Bazant.Z.P和CEB-FIP（90）推荐了混凝土湿度场的非线性湿度扩散系数模型，也是现用干缩模拟的常用模型，利用遗传算法来求解混凝土湿度场特征参数[2]。鉴于湿度特性参数的测量困难，很难进行干缩计算或简单的估算。针对此问题，在参考文献[2]的基础上采用遗传算法和微粒群算法来反演湿度场特征参数，并对反分析方法的精度和适用性进行对比分析，以期为工程设计提供理论依据。

1 计算原理与方法

1.1 湿度场计算

在混凝土中一般认为水分迁移符合Fick定律，其微分方程可以表示为：

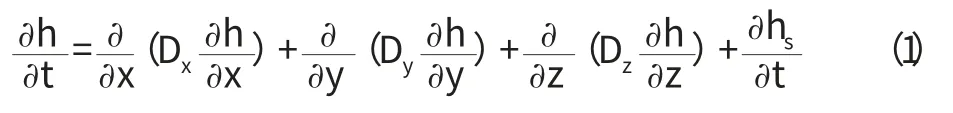
相应的初始条件为：

在与空气接触的边界上，边界条件为：

式中，h为相对湿度，Dx,Dy,Dz是湿度扩散系数，表示为D（h），hs为绝湿环境下水泥水化时消耗湿度，a，b是参数，随水泥品种，比表面积等不同。h0（x,y,z）为已知的相对湿度；β 为表面湿度转移系数；ha为空气的相对湿度。

1.2 反分析基本理论[4，5]

在混凝土湿度场特征参数反演分析过程中，通常采用最小二乘法估计反演参数的适应值，即将实测湿度和有限元计算的湿度差值的平方和作为参数反演的目标函数，来寻求与工程实际条件下混凝土结构湿度变化过程较为接近计算参数，即

式中，X表示反演参数变量；ωij表示在第j时刻第i点的加权系数；Hij表示在第j时刻第i点根据有限元计算得到的湿度值代表在第j时刻第i点实测湿度值；m为观测点的数目；l为某测点观测时间点数目。

在湿度场反分析过程中，需进行迭代计算，选择各种不同的数学优化方法，如传统的模式搜索法、单纯形法、鲍威尔法等，近几年来又出现了神经网络法、遗传算法、粒子群算法等新方法。

遗传算法和微粒群算法是解决最优化问题的有效途径和通用框架，是一种新的全局优化搜索算法，所求出的近似最优解或满意解是人们的主要着眼点之一。本文就这两种算法进行反分析研究以对比其合理性。

2 试验情况

见文[3]中的水灰比0.4的中强度混凝土试块，尺寸为10 cm×10 cm×20 cm，其中一个面散湿，其他绝湿，散湿面为10 cm×10 cm，埋设湿度探头的A，B，C点位于散湿面中轴线上，距离散湿面3 cm，7 cm和12 cm，混凝土试块浇注1 d后拆模，放置在水中浸泡3 d放在相对湿度50%，温度20℃的环境中。试验结果列于表1。

3 反演方法对比

表1 实测的特征点相对湿度表

根据试验浇注块原型建立有限元模型，计算的节点和单元数分别是1089个和800个，在计算的过程中，暴露面按照第三类边界条件处理。

根据实测3个点的湿度，对混凝土自干燥消耗相对湿度的hs=hs∞（1-e-aτb）中的最终消耗湿度hs∞，a和b，以及D1和β 进行了反演分析。浇筑的前三天，时间步长为0.50 d，随后时间步长为1 d，目标优化函数取为其中i为测点号；j为观测时刻和hij分别为实测和计算湿度值；m和n分别为测点数和测次数。

采用遗传算法计算时取交叉概率为70%，变异概率为10%，系数α 取0.10，经过15次的迭代求解，反演辨识的混凝土的最终消耗湿度为hs∞=-0.15，湿度变化规律函数参数a＝0.05和b＝0.79；混凝土的表面湿度转移系数β=2.88×10-4m/d，最大湿度扩散系数D1=3.84×10-5m2/d。采用粒子群算法计算时取加速因子c=2.00，经过13次的迭代求解，hs∞=-0.14，a＝0.04和b＝0.87，β=2.94×10-4m/d，D1=3.92×10-5m2/d。

表2 两种算法的湿度场参数反演计算结果表

对于实际工程来说，模型剖分节点和单元量大，计算时间较长，每减少一次迭代次数都会节约大量的计算时间，从这个方面来说，微粒群算法相比效率较高。而且其计算的精度也较高，本次计算过程中湿度场的计算次数为121，如果提高计算次数，可以得到更优的参数值。

微粒群算法反演出的湿度场参数计算出的特征点相对湿度历时曲线与特征点实测相对湿度历时曲线最贴近，几乎重合。而遗传算法的效果要稍差一些。通过遗传算法反算出的各特征点相对湿度值均低于实测湿度值，但二者发展规律是一致的。

4 结语

根据室内试验实测湿度值，利用遗传算法和微粒群算法对混凝土试块湿度场进行反演计算，并将计算结果和实测数据进行对比，结果表明计算结果跟实际情况相符，说明得到的参数可以反映混凝土湿度扩散规律，为实施防干缩措施提供理论依据。

遗传算法和微粒群算法反演的湿度场和实测相比，微粒群算法计算结果相对更加精确且计算次数较少，收敛速度较快，更适合用于工程反演计算。

[1]牛焱洲，涂传林.混凝土浇筑块的湿度场与干缩应力[J].水力发电学报,1991(2):87-95.

[2]郭利霞，朱岳明，等.基于遗传算法的混凝土湿度场特征参数求解及反分析[J].天津大学学报,2010,43(8):712-716.

[3]Jin-Keun Kim,Chi l-Sung Lee.Moisture diffusion of concrete considering self-desiccation at early ages[J].Cement and Concrete Research,1999,Vol.29:1921-1927.

[4]陈国良,王煦法，等.遗传算法及其应用[M].北京：人民邮电出版社,1996：101-203.

[5]徐果明著.反演理论及其应用[M].北京:地震出版社,2003：1-5.