新密市降水量变化规律的小波分析

□贺会萍（巩义市伊洛河管理所）

0 研究背景

降水量的多少决定着一个地区或流域水资源量的丰富程度。水资源量的变化取决于降水量的变化，因此研究降水量的变化对于水资源安全具有重要的意义。河南省新密市处于半湿润半干旱地区，由于可能的气候变化和包括长期采煤在内的剧烈人类活动对新密市水资源造成严重破坏，造成水资源严重短缺、水环境严重破坏、河流和泉水消失，地下水位急剧下降，对本地区社会经济发展带来严重挑战。

小波分析以其独特的时频局部化优势，在年、月降水量等离散的时间序列分析及预测方面得到了广泛的应用[1-3]。文章采用Morlet复小波作为基函数进行一维连续小波变换,对新密市1960-2010年的年、月降水量时间序列进行时频局部化分析,揭示其在不同时间尺度上的变化规律和突变特征。

1 研究区概况与方法

1.1 新密市气候概况

新密市属暖温带半干旱大陆性季风气候，春夏秋冬四季分明。根据1960-2010年系列统计，多年平均降水量656mm，历史最大年降水量1181mm（1964年），最小年降水量397mm（1986年），相差784mm，年际变化量较大。由于季风气候的影响，降水量时空分布不均。时间上表现为夏季集中、春秋不足、冬季偏少，夏季降水量约占全年降水量的50%，秋季约占25%，春季约占21%，冬季仅占4%左右，汛期6-9月降水量占全年降水量的65.90%左右。空间上表现为以米村—岳村以北及王村—大隗以南山区降水较多，>675mm，中部与东部河谷平原较少；多年平均蒸发量为1662mm。

1.2 小波分析方法

作为信号时频分析的重要实现技术，小波分析通过对母波函数进行伸缩和平移得到小波函数族，再利用这个小波函数族实现对信号滑到逼近，获得函数逼近的程度大小，就是小波变换的系数[4-6]。这个过程就是大家熟知的小波变换，而用小波函数族获得的程度大小，即为小波变换的系统。与传统的傅立叶变换过程相比，小波变换具有近乎完美的时频分析特性。

将小波分析应用到降水量时间序列的分析中，也是近些年水文学研究的热点。通过小波分析可很好去除观测降水量的随机较大波动，识别观测年份中异常水文气象年份，找到相应水文气象的规律。

小波是由满足一定条件的母函数ψ（x）经过收缩和平移得到一个函数族:

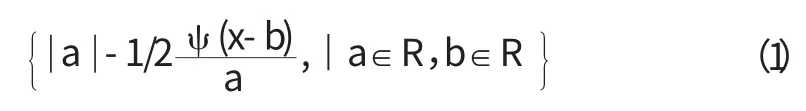
这里母函数必须满足ψ（x）dx=0。

所谓正交小波变换是指高通和低通信道的正反变换核是一样，即每个信道采用标准的正交变换。如果令amn（f）为原信号，则正交小波分解公式如下：

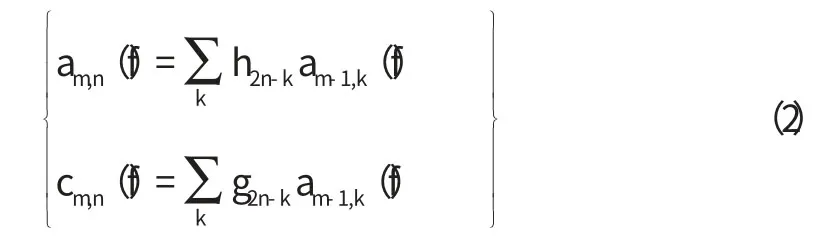
其中g和h分别表示高通滤波器和低通滤波器，应满足关系式:

信号重建的公式为:

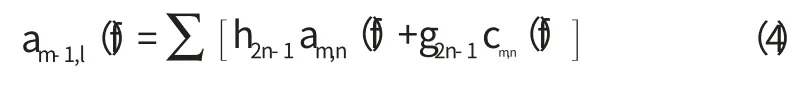
然而，大部分正交小波基是无限支集的，导致相应的高通滤波器和低通滤波器是无限冲激响应，这在计算上是不可行的。虽然Daubechies构造了对应于有限冲激响应滤波器的具有有限支集的正交小波，但由于有限支集小波的非对称性，使对应的高、低通滤波器没有线性相位，需要相位补偿。因此，通过放弃对函数系正交性的要求，可以通过利用双正交小波以达到相位线性和滤波器较短的要求。

鉴于Morlet小波函数的时域和频域具有良好局部特性，文章采用Morlet小波(Morletwavelet)函数对新密市的降水量进行研究。Morlet小波变换系数的实部可表示观测降水量在不同特征在时间尺度上的强弱和相位等两方面的信息，可有效地反映观测降水量的异常年份及其内存规律性。

文章采用Morlet小波(Morletwavelet)函数对新密市的降水量进行研究。Morlet小波是一种单频复正弦调制高斯波,具有很好的时域和频域局部性,常用于复数信号的分解和时频分析。由于Morlet小波的实部本身也是一个对称的小波函数,小波系数的实部可以表示不同特征时间尺度信号在不同时间的强弱和位相两方面的信息。

2 结果与讨论

2.1 月降水量距平值变化特征

新密市1965-2011年逐月降水量距平值变化中,1964年4月出现最大值246.70mm,1987年7月出现最小值-146.40mm,而且月降水距平值出现峰值或谷值的月份通常是在7月或8月,这是因为新密市降水主要集中在6-9月,夏季的降水变化更加明显，汛期降水量占全年降水量的66.10%。为了深入分析长序列条件下，月降水量的变化趋势，文章做出新密市月降水量的累积距平。

1960-2010年期间，新密市降水量累积距平曲线呈现着约为15a的周期性变化，短时间内呈现1a的变化波动，对于后者，可以理解为是降雨量的年际变化特征；而前者反映了降水量的多年变化特征，与降水量的周期性变化有较大的关系。

文章进一步对月降水量累积距平进行小波分析，在计算小波系数时，尺度参数最小值为2个月,最大值设为512个月，根据每个尺度下的小波系数，获得小波系数能量等值线图。通过大量尺度的小波分析，将整个小波变换系数平面的等值线全部绘制出来，其能量聚集点反映了整个观测年份里的变化特征，分别在观测时间1978，1989，2000年等处与分析尺度为217个月的水平叉交地方，存着较小的能量聚焦点。这说明这三个年份相邻的观测年份里，存在着月降水量的突变因素。1978年7月份的降水量达309mm，远高于其相邻月份的降水量；同样地，1990年7月的降水量更高达320.30mm，2000年7月份的降水量高达301.90mm。对于整个小波系数等值线中的山峰，则反映了整个月降水量累积距平在大尺度下的变化趋势，这是一个较为缓慢的变化过程。

2.2 年降水量距平值变化特征

1960年-2010年新密地区的年降水量平均值为656.40mm，最大值为1964年的1180.80mm，最小值为1986年的396.80mm，其降水量距平曲线见图1。从图1可知，1964年的年降水量距平最大，达到524mm；同样，新密市2003年份的年降水量距平也高达462mm，全年降水量为1018mm；1986年的年降水量距平最小，为-259.60mm,在1984，1997年也接近于最小值，表明这些年份比较干旱。

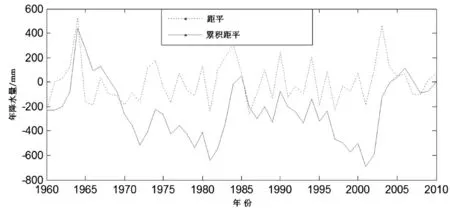
图1 新密地区年降水量的距平与累积距平曲线图

实际上，图1中的新密市年降水量累积距平曲线，则可更好地反映整个观测年份期间的年降水量变化趋势。降水量的距平与累积距平有较好的对应关系，如果降水量连年低于平均值，则累积距平一直下降，反之亦然。1960-1965年连续5a降水量均高于年均降水量，导致累积距平曲线快速爬升；而在接下来的8a中，新密地区的年降水量偏少。从1973-2003年期间，年降水量处在丰水年与枯水年之间交替变化着，直到2003-2005年连续3a的高强度雨水，重新将累积距平曲线拉升到高位。总之，新密地区的年降水量累积距平曲线反映了新密地区的年降水量多年的变化规律与特征。

利用Morlet小波对新密地区年降水量距平进行小波多尺度分析，获得多尺度下小波系数能量等值线图。该小波系数能量等值线图中能量聚集点较多，分布在尺度为4～16的区域内，说明整个新密地区年降水量的波动较大，特别是在小波分析尺度为8a左右范围内，交替分布大小较为均匀的能量聚集点，显示着新密年降水量变化存在一定的周期性，周期约为8年。同时，在尺度为16a的范围内，存在着一个小波能量聚集点以及两个相邻的能量稀疏区域。由小波分析的理论可知，新密地区的年降水量在整个观测年份中存在一个尺度较大丰水期年份，即1982-1985年。

2.3 生长季降水量距平值变化特征

1960-2010年新密地区生长季降水量平均值为491mm,生长季平均降水量占年平均降水量的平均值为75%。由新密地区生长季降水量距平曲线观察，虽然生长季降水量存在个别的高值，但大多数年份生长季降水量低于平均值，并且在1973-2000年期间，生长季降水量存在较大波动，基本上与年降水量距平的波动状况一致。而新密地区生长季的降水量波动进一步显示了丰水年份和枯水年份的长周期变化情况，这个变化趋势则与年降水量的变化趋势一致。与此同时，新密地区生长季降水量距平的小波分析也与年降水量的小波分析结果一致，这说明小波分析的结果源于所分析的数据一致性。

2.4 降水量距平序列典型尺度的过程线及趋势预测

通过分析新密地区月降水量、年降水量以及生长季降水量的小波分析系数方差曲线，可明显地观察到多个极大值点，而这些小波系数极大值点正好对于小波系数等值线中能量聚集的主尺度，则该尺度下的小波分析系数曲线反映了相应降水量变化的主周期。

根据新密地区1960-2010年间的月降水量，获得其累积距平小波分析系数方差曲线，该小波系数方差与尺度曲线拥有2个极大值尺度，即97个月、217个月等两个主尺度。对于小波变换尺度97个月和217月，则说明了在1960-2010年等连续50a的月降水量连续观测，包含者两个主周期变化，其月降水量变化周期分别为97个月或217月，即月降水量主变化周期约为8a和18a，这些主周期变化可反映在这3个典型尺度下的月降水量累积距平小波系数实部变化曲线。接下来，进一步对年降水量小波系数方差曲线进行观察，可发现其包含着3个极大值点，即尺度为4,8和17a，则8a和17a的主尺度与图1显示的月降水量主变化周期8a和18a是一致的。新密地区1960-2010年间的年降水量距平在典型主尺度4,8和17a的小波系数实部变化曲线。同样，新密地区生长季降水量的小波方差曲线也包含着3个主变化尺度，即4,8和17a，得出其相应的生长季小波变换系数实部变化曲线。综上所述，新密地区的月降水量累积距平、年降水量距平和生长季降水量距平，它们的小波系数分析结果，在1960-2010年间整个降水量呈现两个共同的典型变化周期，即8a和17a，反映了新密降水量的变化规律。

3 结论

一是新密市月降水量、年降水量和生长季降水量变化都存在多尺度特征,由这3个降水序列的距平、累积距平和对其小波分析获得的信息相互补充，其联系主要表现在降水量在4，8和17a有周期性特征；二是小波分析可对降水量序列进行多时间尺度分析,为研究气候变化提供了有力手段。

[1]任艳林.1965-2011 年河北塞罕坝地区降水量变化规律的小波分析[J].北京大学学报(自然科学版),2012,48(6)：918-924.

[2]桑燕芳，王中根，刘昌明.小波分析方法在水文学研究中的应用现状及展望[J].地理科学进展,2013,32(9)：1413-1422.

[3] Kisi O. 2009a. Wavelet regression model as an alternative to neural networks for monthly streamflow forecasting.Hydrological Processes,23(25)：3583-3597.

[4] Kisi O.2009b.Neural network and wavelet conjunction model for modeling monthly level fluctuations in Turkey.Hydrological Processes,23(14)：2081-2092.

[5]桑燕芳,王中根,刘昌明.水文时间序列分析方法研究进展[I].地理科学进展,2013,32(1)：20-30.

[6] Kisr, O., Cimen, M., 2012. Precipitation forecasting by using wavelet-support vector machine conjunction model. Engineering Applications of Artificial Intelligence,25(4)：783-792.

[7]Sang,Y.,2013.Areviewontheapplicationsofwavelet transform in hydrology time series analysis. Atmospheric Research, 122：8-15.

[8] Rathinasamy, M., Adamowski,J., Khosa R.,2013. Multiscale streamflow forecasting using a new Bayesian Model Average based ensemble multi-wavelet Volterra nonlinear method.Journal of Hydrology,507：186-200.