汽车P/T灵敏度传递路径分析
2015-08-19侯臣元汪晓虎李建华
侯臣元,汪晓虎,王 亮,李建华
(泛亚汽车技术中心有限公司,上海201201)
汽车P/T灵敏度传递路径分析
侯臣元,汪晓虎,王亮,李建华
(泛亚汽车技术中心有限公司,上海201201)
准确预测车辆内部对发动机力矩输入的声学灵敏度(即P/T)对车辆前期NVH开发具有重要意义,建立详细的整车结构及声腔流体有限元模型,并推导流体—结构耦合有限元方程,进行P/T仿真计算,并在相同边界条件下进行试验。仿真结果与试验值在30 Hz~100 Hz有较好一致性,但在10 Hz~30 Hz低于试验值。通过对传递路径中的悬置隔振及动力总成刚体模态进行仿真与试验对比分析,发现悬置低频动刚度特性对P/T灵敏度有较大影响。根据悬置低频动刚度特性调整悬置动刚度,仿真计算与试验值在整个频带即0~100 Hz皆有较好的一致性。仿真与试验结果为车辆开发前期进行车内噪声水平控制提供一定参考。
声学;有限元法;流体—结构耦合;P/T灵敏度;悬置动刚度
随着汽车在国内的逐渐普及,车辆的NVH (Noise,Vibration,Harshness)性能也越来越得到消费者和汽车厂商的重视。
汽车P/T灵敏度是指在发动机曲轴中心线施加力矩激励,仿真计算或试验测试车内驾驶员或乘客耳旁的声压响应,响应与激励的比值即为P/T灵敏度,单位为dB/Nm。P/T灵敏度与各种工况下的发动机载荷作乘积处理,并根据经验数据进行一定的修正,即可计算得到各种工况下的车内声压水平。在车辆开发前期,利用仿真计算P/T灵敏度对整个传递路径进行分析优化具有重要意义,可以有效地控制车内的振动和噪声水平。目前,国内外对从悬置车身侧安装点到车内方向盘和座椅的振动传递路径进行了较多研究,减少各结构和子系统之间模态频率耦合或者增加结构刚度来降低方向盘或座椅振动幅值[1-3];对振动传递路径中的悬置进行深入的研究,使悬置可以更好地衰减动力总成传递过来的振动[4-7];对车辆单一工况如怠速工况下的车内振动特性进行研究等[8,9]。但较少有在一个较宽频带上(如0~100 Hz)对从动力总成输出力矩激励到车内声学响应整个路径进行研究,并对仿真计算和试验测试之间的差别进行原因分析。
基于某乘用车型,本文利用流体—结构有限元模型计算P/T灵敏度;对有限元计算结果进行试验验证,并分析仿真计算结果与试验结果之间差异的原因,为计算出正确的P/T灵敏度和在车辆研发前期进行车内噪声水平控制提供参考。
1 整车有限元模型及流体—结构耦合有限元理论
1.1整车有限元模型
整车结构有限元模型含白车身,动力总成,前后悬架系统,转向系统,轮胎,车门,天窗,车内座椅,排气系统,油箱,车内饰板,吸隔声材料及各种附加质量等。大部分系统建立详细的有限元模型,部分系统采用集中质量或分布式质量表示。
为增加整车结构有限元模型的正确性,利用模态置信准则(Modal assurance criterion,MAC)比较分析仿真计算与试验测试的若干车身结构主要模态。如果两个模态振型是线性相关的,则MAC值接近1,如果两个模态振型不具有相关性,则MAC值接近于0。MAC值计算公式如下

式中“H”代表共轭转置。

表1 仿真与试验中的主要车身结构模态对比

表2 仿真与试验中的车身结构主要模态MAC值对比
1.2声腔流体有限元模型
声腔流体有限元模型包括车室空腔子模型,座椅子模型,车门空腔子模型,IP空腔子模型等,并分别对不同子模型赋予不同的材料密度,声速及阻尼等参数,以表征各个空腔的特性;同时,根据声能在不同子模型间流动特点,在每个子模型之间建立耦合区域。流体单元类型为四面体单元。
1.3有限元流体—结构耦合方程
将车身结构视为弹性体,车身受到外界激励后引起车身板件的振动,车身板件的振动会引起车内空气流体的振动,而空气流体的振动反过来又作用于车身板件上面,于是车身板件与车内空腔形成了一个流体—结构耦合的声场系统。
边界存在阻尼时衰减波动的有限元方程为

式中[MeP]为单元流体质量矩阵;[CeP]为单元流体阻尼矩阵;[KeP]为单元流体刚度矩阵;ρ0{Re}T为单元耦合质量矩阵;{Pe}为节点压力向量;{Ue}为节点位移分量向量。
考虑作用于界面上流体压力载荷{FePr}影响的结构振动方程为
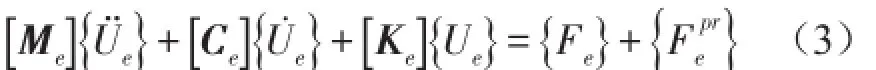

式中{N'}为位移单元形函数;{n}为界面单位法线。
将用于压力空间变化的有限单元形函数方程P={N}T{Pe}代入(4)式,生成新的界面流体压力载荷向量{FeP
r}

式中{N}为压力单元形函数
推导得出考虑界面压力的结构振动方程为

将式(2)与(6)联立可得到完整的流体—结构耦合有限单元离散化方程,即

2 P/T灵敏度仿真及试验验证
2.1声学灵敏度传递函数
在动力总成曲轴中心位置施加一绕曲轴轴线的宽频力矩激励T,该激励引起动力总成振动并通过悬置系统传递到副车架或车身,继而通过一系列传递路径传递到车身空腔板件,引起车身空腔板件振动,从而向车内辐射声音;车内空气流动反作用于声腔板件,形成流体—结构耦合的声场系统;通过流固耦合仿真分析或试验获得驾驶员或乘客处的声压P,可得声学灵敏度传递函数H(f),如式(8)所示

2.2声学灵敏度仿真及试验验证
基于所建立的整车有限元模型,仿真计算P/T灵敏度。计算输出的车内声学响应频率范围为0~100 Hz,考虑高频模态对低频响应的影响,设置整车结构模态和声腔模态计算频率范围分别为0~200 Hz和0~400 Hz。本文仅选择有代表性的车内第2排左侧乘客右耳(2 LE)和第三排中间乘客右耳(3 ME)处的响应进行分析,计算结果如图1和图2中实线所示。
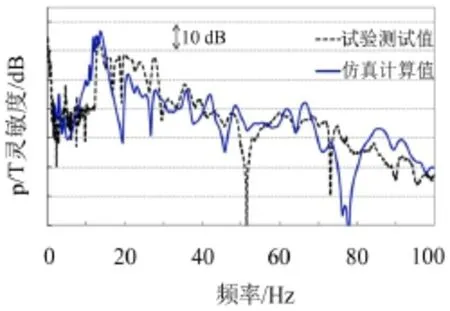
图1 2 LE位置P/T灵敏度
在相同的边界条件下,对仿真计算进行试验验证。在动力总成下表面纵向布置两个激振器,每个激振器通过一柔性顶杆与动力总成相连,通过输入两个大小相等、相位相反及垂直向上的力来模拟力矩输入。在车内驾驶员及乘客右耳位置布置麦克风来拾取车内的声学响应。
激振系统采用德国TIRA公司的激振器及功率放大器,其有效工作频率范围为0~5 000 Hz;力传感器为PCB通用石英力传感器,可以承受445 N的压力或拉力且有好的低频响应特性。利用PCB随机入射场传声器及ICP前置放大器接收车内声学信号,其有效工作频率范围为6.3 kHz~12.5 kHz。同时,采用LMS SCADAS III前端及LMS Test.Lab软件进行信号的采集与处理。试验结果如图1和图2中的虚线所示。
从仿真计算曲线和试验曲线比较结果可以看出,在30 Hz~100 Hz频率范围两者的一致性较好,但在15 Hz~30 Hz频率范围仿真计算结果要小于试验测试结果。而根据式(9)可知,对4缸发动机,15 Hz~30 Hz恰为车辆怠速时发动机基频激励范围。

图2 3ME位置P/T灵敏度

式中N为发动机气缸数;n为发动机转速,单位为r/min;τ为内发动机冲程系数,四冲程τ=2。
因此,研究仿真计算与试验差别的原因,提高15 Hz~30 Hz仿真计算的准确性对车辆怠速NVH性能前期开发具有重要意义。由于仿真计算与试验测试具有相同的边界条件,且激励输入经证明也具有一致性,因此重点对振动向车内传递的路径进行分析。将整个传递路径分为3个阶段,分别是悬置PT侧支架到悬置车身侧支架,悬置车身侧支架到悬置车身板件,车身板件到车内声学响应位置。
3 悬置隔振仿真与试验对比分析
3.1悬置隔振仿真计算
在仿真计算时,在悬置PT侧支架及车身侧支架分别选择响应输出点,输出两个位置的加速度响应。为减小仿真中的扰动误差,在响应输出点处选择4个节点建立RBE 2连接,输出其自动计算出的中心点响应。在选择响应输出点时,应选择适于布置传感器的位置,以便于试验测试时布置传感器。
本文所基于的车型,PT(Power train,动力总成)通过4个悬置与副车架或车身前纵梁连接,分别是发动机悬置,变速箱悬置,前悬置及后悬置。仿真计算时,每个位置输出XYZ三个方向的振动响应,在悬置PT侧及车身侧分别输出12条响应曲线。
对悬置PT侧响应,这12条曲线在随频率变化趋势上具有较高的一致性;对悬置车身侧响应,12条曲线也具有较高一致性,但前悬置及后悬置车身侧振动响应幅值高于其它两个悬置,同时在60 Hz附近有一峰值,这是由于前悬置及后悬置安装在刚度较低的副车架的原因,60 Hz左右为副车架模态。变速箱悬置PT侧振动响应如图3所示,车身侧响应如图4所示。

图3 变速箱悬置PT侧振动响应
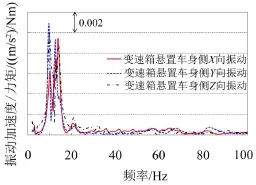
图4 变速箱悬置车身侧响应
由图3可以看出,悬置PT侧响应的峰值集中在7 Hz~17 Hz,而30 Hz~100 Hz响应接近平滑的直线。由图4可以看出,对悬置车身侧响应,其峰值也主要集中于7 Hz~17 Hz,由于悬置的隔振作用,虽然该频段的峰值频率没有改变,但振动幅值在降低的同时,不同频率的幅值也有了相对变化;对30 Hz~70 Hz,由于车身等结构和声腔流体模态的存在,这个频段的幅值变化与悬置PT侧响应变化明显不同,这些峰值频率与车身结构等的模态频率对应。
3.2悬置隔振试验研究
在悬置的PT侧及车身侧布置加速度传感器,传感器安装位置与仿真计算时响应输出位置相同,测试这些位置的振动加速度响应,计算得到加速度响应与力矩输入的频响曲线,单位为((m/s2)/Nm)。
测试得到各个悬置两侧的加速度响应,图5和图6分别为变速箱悬置的PT侧和车身侧的振动响应。
对比分析图5与图3,可以看出两者在30 Hz~100 Hz的变化趋势是一致的,但在0~30 Hz,两者有比较明显的不同,试验测试的峰值频率主要出现在10 Hz~25 Hz。
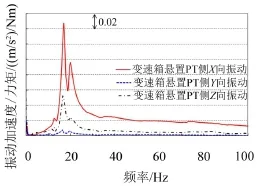
图5 变速箱悬置的PT侧振动响应
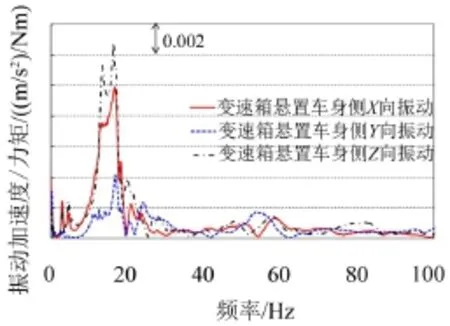
图6 变速箱悬置的车身侧振动响应
3.3 PT刚体模态仿真与试验对比分析
在整车边界条件下,仿真计算动力总成刚体模态,与P/T试验测试时的动力总成刚体模态进行对比分析,如表3所示。

表3 动力总成刚体模态仿真计算值与试验值对比
由表3可以看出,试验测试得到的发动机刚体模态频率整体上要高于仿真计算结果。发动机刚体模态频率偏高必然会导致传递到悬置PT侧的振动响应峰值频率偏高,继而传递到悬置车身侧的响应峰值偏高,经过车身路径传递后,车内的声压响应峰值频率也会偏高,即表现为在20 Hz~30 Hz,试验P/ T灵敏度要大于仿真计算值。
在PT质量及转动惯量、悬置布置形式和连接点刚度等一定情况下,PT刚体模态频率及振型主要和悬置的各向刚度有关。一般情况下,悬置刚度会在设计值±20%范围内,但悬置低频液压特性及试验过程中悬置某个方向振动位移过大会对悬置刚度产生较大的影响。图7为变速箱悬置动刚度液压特性变化曲线,图8为P/T试验时变速箱悬置振动位移曲线。

图7 液压悬置动刚度特性曲线
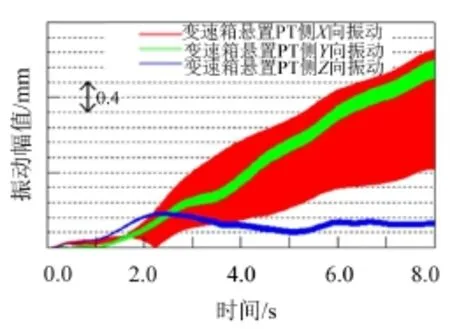
图8 P/T试验变速箱悬置振动位移曲线
由图7可以看出,液压悬置刚度在10 Hz~20 Hz有比较急剧的变化,而仿真时悬置刚度一般为一定值。从图8中可以看出,在P/T试验时,变速箱悬置X向位移随时间变化比较大,这会造成悬置在该方向的刚度变化,这也是两者之间差别的一个重要原因。
4 悬置刚度调整后仿真计算与试验对比
考虑液压悬置低频动刚度特性,调整变速箱悬置在X向的动刚度为原动刚度的1.7倍,计算发动机刚体模态频率及振型,如表4所示。
可发现调整后仿真计算的PT pitch模态和Yaw模态与试验测试值比较接近。基于此刚度,计算P/T灵敏度,并与试验值做对比,如图9和图10所示。
可以看到,在0~100 Hz整个频段上仿真计算值和试验值有较好的一致性。
目前,各主要有限元计算软件推出的新版本中已考虑弹性件的动刚度特性,但仍有其局限性。如何在一较宽频带上更准确地模拟液压悬置的动态特性,还需要与之相关的企业和研究机构做更多的研究。

表4 动力总成刚体模态仿真计算值与试验值对比

图9 悬置刚度调整后2 LE P/T灵敏度对比
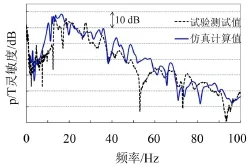
图10 悬置刚度调整后3 ME P/T灵敏度对比
5 结语
(1)基于某乘用车型,建立整车流体—结构有限元模型,对发动机力矩激励下的车内声学响应即P/T灵敏度进行仿真计算,并与试验进行对比分析。在10 Hz~30 Hz范围内仿真计算值小于试验测试值,而在30 Hz~100 Hz范围内两者有较好的一致性;
(2)对悬置隔振进行仿真计算并与试验对比分析,结果表明仿真频响曲线峰值频率分布于7 Hz~17 Hz,而试验测试频响曲线峰值频率主要分布于10 Hz~25 Hz;
(3)仿真与测试的PT刚体模态频率分布与(2)中的峰值频率分布有相同的趋势;
(4)液压悬置低频动刚度特性及悬置在某一方向的振动大位移会改变悬置动刚度,从而改变PT刚体模态的频率和振型,继而影响低频P/T灵敏度。如何在一较宽频带上更准确地模拟液压悬置的动态特性需要业界进行更多研究;
(5)根据悬置动刚度特性对悬置刚度调整后,仿真计算的P/T灵敏度和试验测试值有较高的一致性。
[1]Kim K C,Choi I H,Kim C M.A study on the advanced technology analysis process of steering system for idle performance[J].SAE Paper,2007-01-2339.
[2]赵静,周鋐,梁映珍,等.车身板件振动声学贡献分析与优化[J].机械工程学报,2010,46(24):96-100.
[3]刘建伟,刘二宝,王志亮,等.轿车驾驶室声学响应仿真分析[J].噪声与振动控制,2012,32(4):103-106.
[4]成义权,陈剑,张要思.动力总成悬置系统隔振优化与工程应用[J].噪声与振动控制,2013,33(6):100-105.
[5]马天飞,胡杰宏,王登峰,等.液压悬置元件幅变特性的研究[J].汽车工程,2013,35(7):604-607.
[6]李建康,郑立辉,宋向荣.汽车发动机悬置系统动刚度模态分析[J].汽车工程,2009,31(5):457-461.
[7]Shangguan Wenbin,Lu Zhenhua.Modeling of a hydraulic engine mount with fluid-structure interaction finite element analysis[J].Journal of Sound and Vibration,2004,275:93-221.
[8]高传宝,汪晓虎,高亚丽.利用A/T模型分析整车怠速振动性能[J].汽车工程,2009,39(11):1056-1059.
[9]史文库,邬广铭,陈志勇,等.商用车发动机怠速运转方向盘抖动控制研究[J].振动与冲击,2013,32(8):189-192.
Analysis of Vehicle's P/T Sensitivity Based on Transfer Path Method
HOU Chen-yuan,WANG Xiao-hu,WANG Liang,LI Jian-hua
(PanAsia TechnicalAutomotive Centre Co.Ltd.,201201 Shanghai,China)
It is important to accurately calculate the sound pressure in vehicles induced by the powertrain torque excitation for advanced vehicle development.In this paper,a detailed finite element model for whole vehicle structure including the fluid in the acoustic cavity was established.The fluid-structure coupled finite element equations were formulated.The model was validated with the method of modal assurance criterion.Based on the model,the acoustic sensitivity defined by sound pressure over torque,P/T,was calculated.The test was carried out under the same boundary condition.It is shown that the simulation result has a good agreement with the test result in 30 Hz-100 Hz frequency range,while in 10 Hz-30 Hz frequency range the simulation result of P/T is lower than that of the test.The simulation and tests of the mount isolation and powertrain rigid-body modals were completed and the results were analyzed.It was found that the mount low-frequency dynamic-stiffness characteristics have large influence on P/T.When the mount dynamic-stiffness value increases,the P/T results of simulation and tests have a good consistency in whole frequency band of 0-100 Hz.
acoustics;finite element method;fluid-structure coupling;P/T acoustic sensitivity;mount dynamicstiffness
O422.6
ADOI编码:10.3969/j.issn.1006-1335.2015.05.024
1006-1355(2015)05-0116-05+120
2015-02-10
侯臣元(1980-),男,山东省滨州市人,硕士生,主要研究方向:汽车振动噪声。
E-mail:hcy31311@163.com
