波浪型斜拉索涡激振动实验研究

邹　琳，胡　勇，王汉封，汪　秒，徐汉斌

（1.武汉理工大学　机电学院，武汉430070；2.中南大学　铁道学院风洞实验室，长沙410000）

波浪型斜拉索涡激振动实验研究

邹琳1，胡勇1，王汉封2，汪秒1，徐汉斌1

（1.武汉理工大学机电学院，武汉430070；2.中南大学铁道学院风洞实验室，长沙410000）

针对目前改变斜拉索表面形状来抑制斜拉索由风载荷引起的振动所遇到的问题，采用热线风速仪、激光位移器测量和烟线等实验方法，实验研究在Re=6 800～20 480区域内波浪型斜拉索涡致耦合振动及频率“锁定”现象，并引入直斜拉索作为对比。实验表明：在相同的质量比和阻尼比下，波浪型斜拉索λ/D=2和λ/D=6同直斜拉索同样容易被诱导振动，波浪型λ/D=2比波浪型λ/D=6的减震效果要好，和直斜拉索相比，波浪型λ/D=2的诱导振动时最大振幅减小10%，锁定区间变短，主要是由于随着表面凹凸变化倾斜度较大，波浪型斜拉索表面的展向二次涡强度得以增强，一旦诱导振动，将干扰斜拉索的涡旋激励，从而达到减震的目的。

振动与波；波浪型斜拉索；涡激振动；阻尼比；抑振；实验研究

当流体绕过钝体时，在一定流动工况下钝体两侧会发生旋涡脱落的现象，交替的涡脱会诱发结构物在与来流垂直方向上产生周期性变化的流体作用力，致使结构物产生振动，严重时会使结构物损坏。这类涡激振动问题的研究已经成为基础研究和工程领域中有意义的课题之一［1，2］。

斜拉桥是现代大跨度桥梁的主要桥型之一，由于斜拉索具有柔度大、质量轻、阻尼小等特性，使其在风载激励下容易发生涡激振动（Vortex-induced Vibration）。由涡脱产生的大振幅振动易使柔性斜拉索发生疲劳损坏，严重时还会造成拉索失效［3］，面对这些现象，采取必要的控制措施已迫在眉睫。

涡激振动是一个非常复杂的流固耦合问题［4，5］，它涉及到许多学科，其中包括流体力学、结构力学、振动学、计算流体力学等。当流体的泻涡频率和结构的自振频率相近时，就会发生所谓的“锁定”（Lock-in）现象使得结构振动的幅值明显增大。近年来研究结果表明［6］:改变钝体表面形状或附加额外的装置可以改变绕流场，改变旋涡的形成和发展过程，从而达到减阻、减振的目的。LAM K.和Lin Y.F.［7］数值模拟发现在Re=80～150时，波浪型斜拉索静止绕流的三维尾迹涡结构由于展向三维涡的产生能够得到很好的控制，有效延缓绕流场附面层的分离，可以减少其所受到的阻力和升力。ZOU L和Lin Y. F.［8，9］数值计算了Re=3 000时，波浪型斜拉索同样具有减阻减振效果。Feng［10］和Williamson［11］分别对大质量比和小质量比的直斜拉索圆柱模型进行了涡激振动的实验研究，得到涡激振动的锁定区间和振幅会随着质量比和阻尼比的变化而变化，不同的振幅分支会出现相应的2S、2 P涡脱模式。但是波浪形状对于斜拉索涡激振动的影响机制，国内外尚未见文献报导，本文通过实验方法，采用弹性阻尼系统研究两种典型的波浪型斜拉索λ/D=2和λ/D=6涡激振动机制，并探明它们的减阻减振情况。

1　风洞实验台

1.1实验几何模型

如图1为波浪型斜拉索的几何模型示意图，其几何表面形状由下式表述Dz=Dm+2acos（2πz/λ）（1）

Dm=（Dmax+Dmin）/2（2）式中Dz为波浪型斜拉索轴向直径，Dm为波浪型斜拉索的平均直径，Dmax为波浪型斜拉索轴向方向的最大截面直径，Dmin为其最小截面直径，a为波浪型斜拉索表面余弦曲线的幅值，λ为波长，两种不同形状的波浪型斜拉索几何特征尺寸如表1所示，同时引入直径Dm直斜拉索作对比研究，所有尺寸采用Dm进行无量纲化处理。

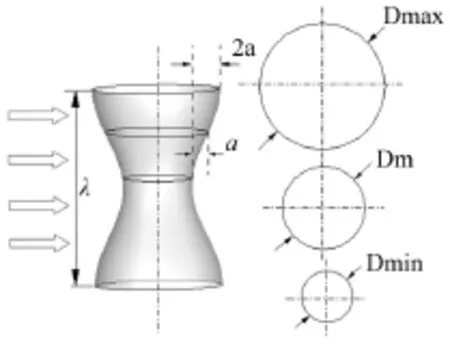
图1　波浪型几何模型

三种模型的质量比m∗为振动结构体的总质量与其排开流体质量的比值，近似一样m∗=4M/（πD2Lρ）≈50.36，雷诺数变化区间Re=6 800 ～20 480，阻尼比ξ=0.001 2。

1.2实验装置

实验在循环式小风洞（0.45 m×0.45m×2 m）实验台上进行，其风速v可在0～40 m/s范围内连续变化。在实验风速范围内，壁面的边界厚度约为20 mm，风速工作段的湍流度在0.2%以内，最大阻塞度为4%。采用铝合金型材搭建实验架，用机型夹将实验架固定在实验台上，采用3D技术打印三种不同形状的斜拉索实验模型，将斜拉索模型放在风洞试验段中心，上下分别吊2根弹簧，沿流向两端采用细绳限制它的流向自由度，缓慢增加风速，直到看到实验模型振动的现象。实验用到的仪器有：热线风速仪、激光位移器、烟线。

表1　实验模型的几何特征尺寸

图2　波浪型斜拉索涡激振动实验建模

2　结果与讨论

2.1斜拉索涡激振动锁定区域

图3为不同形状的斜拉索涡激振动下诱导振幅曲线，并引入Feng［10］和Williamson［11］对直圆柱的实验研究结果作为比较，其中Feng［10］的质量比m∗= 258，质量比m∗比较大，振幅曲线出现两个分支，最大振幅约为0.6 D；Williamson［11］文献中m*=2.4，质量比m*比较小，振幅曲线出现三个分支（且两个分支之间存在明显不连续）：初支、上支和下支，最大振幅高达0.9 D，锁定区间也变得更长，并且随着约化速度的增加，一直保持着一段小幅度振动。m*越小，涡激共振的区间就越长；m∗×ξ越小，最大振幅就越大。并且Williamson还发现从初支到上支之间的相互转变，振幅会出现“滞后”现象，从上支到下支之间的转变存在相位的跃变。本文的m*为50.36，实验研究得出直斜拉索同样具有三个分支，锁定区域在约化速度Ur为3～12之间，上支的最大振幅达到0.7 Dm，近似于Williamson的结果。Sarpakaya［12］在Re=6 000 ～35 000，m∗×ξ=0.052，最大振幅达到0.95 D，本文的m∗×ξ=0.071，相对较大，同样说明了实验数据的可靠性。

图3可以看出，波浪型斜拉索振动同样存在三个分支，说明波浪型斜拉索在相同质量比和阻尼比的条件下也容易被诱导发生振动，λ/D=6的斜拉索在振动幅度上和直斜拉索基本一致，振动锁定区间也很相似，都是约化速度Ur从3到11的变化区间。相比于λ/D=6，λ/D=2的斜拉索减振效果要好，上支最大振幅接近0.6 D，相对于直斜拉索减小了10%，振动锁定区间也变短了，在约化速度Ur=10的时候诱导振动就停止了。

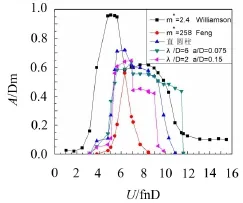
图3　不同形状斜拉索涡激振动下诱导振幅曲线

2.2直斜拉索涡激振动下尾流涡结构

直斜拉索静止时，后尾迹形成稳定的涡结构（图4（a））；随着风速的增加，逐渐形成2S的涡脱模式（图4（b）），涡变得密集且在一个振动周期内连续脱落两个单涡，并靠近中心线排列着；进一步增加风速，振动幅度变大，涡向两边分离，尾迹变宽，出现两列平行的涡（图4（c））；当振幅达到最大时，斜拉索模型尾流会出现2P的涡脱模式（图4（d）），一个周期内脱落两对涡，一直持续到振动减弱，这些流动现象与文献［13］一致。

图4　直斜拉索涡激振动下尾流涡结构

2.3波浪型斜拉索涡激振动下尾流涡结构

LAM K.和Lin Y.F.［14］大涡模拟了静止波浪型圆柱绕流，发现在的波浪型圆柱能达到18%的最佳减阻效果。波浪型斜拉索表面形状随展向变化，导致相对稳定的三维剪切层，将改变拉索表面的压力分布，能起到减阻效果。图5为波浪型斜拉索（λ/D=2）的尾流涡结构演变过程，从中可以发现：波浪型λ/D=2斜拉索，大截面和小截面的涡脱形态基本同步，涡结构尽管比较类似，但大截面后尾迹较小截面后尾迹宽，这可归因于展向波浪形状导致了大、小截面不同的流动分离点。相比于直斜拉索，波浪型斜拉索λ/D=2的振幅减小了10%（图3），主要是由于随着表面凹凸变化，倾斜度较大，波浪型斜拉索表面的展向二次涡强度得以增强，一旦诱导振动，将干扰斜拉索的涡旋激励，从而达到减震的目的。而波浪型λ/D=6斜拉索其最大截面和最小截面的尾流涡结构，基本和直斜拉索一致，可能是由于其沿展向方向表面变化平缓。

2.4波浪型斜拉索涡脱频率

图6可以看出在锁定区域内直斜拉索、波浪型λ/D=6和波浪型λ/D=2的锁定频率基本保持在7.4 Hz左右，波浪型λ/D=2离开振动区间后涡脱频率略高于直斜拉索，而且大小截面的涡脱频率基本一致。这也很好的支持了本文提出的两个不同形状的波浪型斜拉索减阻抑振效果不是很明显的结论。

3　结语

实验研究了两种典型的波浪型斜拉索λ/D=2 和λ/D=6涡激振动机制。在临界雷诺数下，对于相同的质量比和阻尼比，所提出的两种不同形状的波浪型斜拉索和直斜拉索同样会被诱导振动。在锁定区间里，涡脱落模式基本一致，涡脱频率近似。波浪型λ/D=2斜拉索比λ/D=6斜拉索抑振效果相对较好，主要是由于随着它的表面凹凸变化，倾斜度较大，波浪型斜拉索表面的展向二次涡强度得以增强，一旦诱导振动，将干扰斜拉索的涡旋激励，从而达到减振的目的，导致振幅减小10%，振动区间也缩短。波浪型斜拉索的表面形状与雷诺数对于其涡激振动以及振动状态下响应是一个耦合的影响，其影响机制仍需进一步探索。

图5　波浪型λ/D=2斜拉索的尾流涡结构演变过程

图6　直斜拉索和波浪型斜拉索涡激振动下的涡脱频率示意图

［1］徐枫.结构流固耦合振动与流动控制的数值模拟［D］.哈尔滨：哈尔滨工业大学，2009.

［2］周国成.圆柱涡激振动数值模拟研究［J］.噪声与振动控制，2010，30（5）：51-59.

［3］李春祥，李薇薇.斜拉索风致振动疲劳的分析［J］.振动与冲击，2009，28（9）：135-139.

［4］Jauvtis N，Williamson C H K.Vortex-induced vibration of a cylinder with two degrees of freedom［J］.Journal of Fluids and Structures，2003，（17）:1035-1042.

［5］Williamson C H K，Govardhan R.Vortex-induced vibration ［J］.Annual Review of Fluid Mechanics，2004（36）:413-455.

［6］Raghavan A Kumar，Chan-Hyun Sohn，Bangalore H L Gowda.Passive control of vortex-induced vibrations:an overview［J］.RecentPatentsonMechanical Engineering，2008，（1）:1-11.

［7］Lam K，Lin Y F.Effects of wavelength and amplitude of a wavy cylinder in cross flow at low Reynolds numbers［J］. Journal of Fluid Mechanics，2009，（620）:195-220.

［8］邹琳，林玉峰.亚临界雷诺数下波浪型圆柱绕流的数值模拟及减阻研究［J］.水动力学研究与进展，2010，25（1）：31-36.

［9］Zou L，Lin Y F.Force reduction of flow around a sinusoidal wavy cylinder［J］.Journal of Hydrodynamics，2009，21:326-335.

［10］Feng C C.The measurement of vortex induced effects in flow past stationary and oscillating circular and d-section cylinders［D］.The University of British:Department of Mechanical Engineering，Columbia，Canada，1968.

［11］C H K Williamson，R Govardhan.A brief review of recent results in vortex-induced vibrations［J］.Journal of Wind Engineering and Industrial Aerodynamics，2008，（96）: 713-735.

［12］Sarpakaya T.A critical review of the intrinsic nature of vortex-induced vibrations［J］.Journal of Fluids and Structures，2004，（19）:389-447.

［13］Khalak A，Williamson C H K.Motions，forces and modes transitions in vortex-induced vibrations at low massdamping［J］.Journal of Fluids and Structures，1999，（13）:813-851.

［14］Lam K，Lin Y F.Large eddy simulation of flow around wavycylindersatasubcriticalreynoldsnumber［J］. International Journal of Heat and Fluid Flow，2008，（29）:1071-1088.

Experimental Study on the Vortex-induced Vibration of Wavy Stay Cabl

ZOU Lin1，HU Yong1，WANG Han-feng2，WANG Miao1，XU Han-bin1
（1.School of Mechanical and Electronic Engineering，Wuhan University of Technology，Wuhan 430070 China；2.Wind Tunnel Laboratory，Railway Institute，Central South University，Changsha 410000，China）

Considering the existing challenges in wind-induced vibration control of flexible stay-cables，a new modified wavy stay-cable was proposed to suppress the vibration and reduce the cable drag.By using hot-wire anemometer，laser displacement sensor，pressure scanning valve，smoke wire and some other experimental methods，the vortex-induced vibration （VIV）and the frequency lock-in phenomenon of the wavy stay cables at Re=6800-20480 were studied.The results were compared with those of the regular stay cable.The experimental results indicated that similar to the straight stay cable，the wavy stay cable withλ/D=2andλ/D=6can be induced the vibration easily at the same mass ratio and damping ratio.However，the vibration suppression effect of the wavy stay cables still exists.The vibration suppression effect of the wavy stay cable with λ/D=2is better than that of the wavy stay cable withλ/D=6.Compared with the straight stay cable，the maximum amplitude of the vortex-induced vibration can be reduced by 10%for the wavy-stay-cable，and the lock-in region is shortened. One of the main reasons is that the large variation of the modified wavy stay-cable surface can enhance the secondary spanwise vortex.Once the vortex vibration is induced，the large variation of the modified wavy stay-cable surface will interfere the vortex excitation so that the vortex shedding is controlled and the lift fluctuation is suppressed.

vibrationandwave；wavystaycable；vortex-inducedvibration；dampingratio；vibrationsuppression；experiment

TU311.3

ADOI编码：10.3969/j.issn.1006-1335.2015.05.040

1006-1355（2015）05-0189-04

2014－12－22

国家自然科学基金项目（11172220）

胡勇（1988－），男，湖北武汉人，研究生，主要研究方向：流体诱导振动控制。

邹琳，女，研究生导师。

E-mail:l.zou@163.com