动力柔化直板叶片动力学相似关系

赵晓宇，黄　海，曲　涛，郭　健，罗　忠

（1.中航工业集团沈阳发动机设计研究所，沈阳110042；2.空军驻沈阳地区代表室，沈阳110031；2.东北大学　机械工程与自动化学院，沈阳110819）

动力柔化直板叶片动力学相似关系

赵晓宇1，黄海1，曲涛2，郭健3，罗忠3

（1.中航工业集团沈阳发动机设计研究所，沈阳110042；2.空军驻沈阳地区代表室，沈阳110031；2.东北大学机械工程与自动化学院，沈阳110819）

针对考虑动力柔化效应的直叶片动力学相似模型设计的问题，提出一种考虑动力柔化效应的动力学相似模型设计方法。根据大范围运动板的动力方程推导得到的矩形板动力平衡方程，结合直叶片运动特性，建立基于柔性体假设的直叶片动力平衡方程；运用相似原理，建立考虑动力柔化的旋转柔性直叶片的动力学相似关系；通过分析所建立的相似关系，为了避免过高转速引起试验系统的高阶振动，提出建立旋转直叶片过渡试验模型的方法，并分析其在直叶片刚性与柔性条件下的适用性；最后通过数值验证相似关系的有效性和正确性。

振动与波；动力柔化；旋转叶片；试验模型；动力学相似；过渡模型

叶片是旋转机械如航空发动机、压缩机和汽轮机等大型旋转机械装备中的关键部件，由于其工作环境复杂，动力学问题很难用数学方法完全解决，必须通过物理试验来研究。然而在工程实际中，直接采用原型实验往往由于几何尺寸、材料成本、实验周期以及实验难度等问题难以进行，因此通常考虑采用相似试验模型进行实验。

对叶片相似试验模型的研究，国内外学者做了很多工作。郝燕平［1］对压气机叶片所涉及的几个结构相似性问题进行理论研究，讨论在保持气动相似的条件下，模型叶片和原型叶片之间静强度、振动特性、振动响应的相似性问题；罗忠［2］针对复合材料层合板类结构的相似模型设计问题，提出在固有特性相似条件下，畸变模型几何尺寸区间的确定方法；陈小波［3］通过研究考虑旋转叶片的离心刚化效应对叶片动力特性的影响，引入刚化系数，给出频率修正公式；Friedmann［4］通过相似模型实验与计算机仿真对比的方法，分析直升机旋转叶片的气动弹性特性等等。而对考虑叶片动力柔化效应的相似试验模型研究文献尚不多见。

叶片有刚性叶片和柔性叶片之分，刚性叶片作为刚体可不考虑旋转时动力柔化效应，而柔性叶片作为柔性体工作时需考虑由转速引起的变形效应影响，即动力柔化效应影响。对于高速旋转叶片，其动力柔化效应对其动力特性影响不容忽视，柔化效应会增大叶片原有的自振频率，严重时使得叶片不能正常工作。本文基于相似理论，建立考虑动力柔化效应的旋转直叶片动力学相似关系，为叶片相似试验模型研究提供一定理论补充。

1　动力平衡方程

矩形薄板的运动变形如图1所示。图中OXYZ为惯性参考系，其上建立非惯性参考系oxyz，板中面上的一点P0变形后为P，r、s分别为P点沿矩形板长度和宽度方向上的总伸长量，u1、u2、u3分别为x、y、z方向上的变形量。e1、e2、e3分别为x、y、z方向的单位向量。

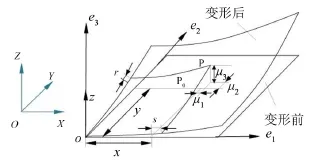
图1　矩形薄板的运动变形图

根据薄板变形理论［5］，由几何应变位移关系可知

式（1）中，x、y为板上任一点坐标。

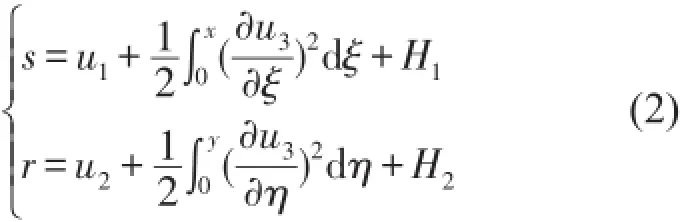
根据泰勒公式可将式（1）展开得式（2）中，H1、H2为高阶小量。

忽略式（2）中高阶小量，并将式（2）对时间t求导可得非惯性系统中x、y方向的速度为

利用Rayleigh-Ritz法求解大范围运动板的平衡方程，设

式（4）中，ϕ1j（x，y）、ϕ2j（x，y）为j阶纵向振动振型函数，ϕ3j（x，y）为j阶横向振动振型函数，qj（t）为广义坐标，μn为总的振型函数个数。

矩形薄板的动力方程为［6，7］：

式（5）中，a、b、h分别为薄板的宽度、长度、厚度；ρ0为薄板单位面积质量；E为薄板材料弹性模量；μ为薄板材料泊松比；G为薄板的剪切模量，ϕi，x、ϕi，y分别为第i阶振动振型函数对x和y的一阶偏导；ϕi，xx、ϕi，xy、ϕi，yy分别为第i阶振动振型函数对x、y的2阶偏导；ω1、ω2、ω3分别为绕X、Y、Z轴旋转的角速度；v1、v2、v3分别为薄板上点的速度。

联立式（5）、（6）、（7）可求解位移函数s（x，y，t）、r（x，y，t）、u3（x，y，t）。

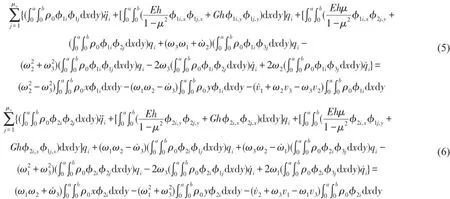
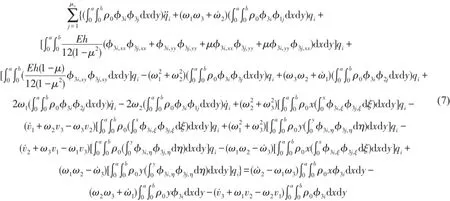
对如下图2所示的悬臂矩形板模型的直叶片，R0为叶根半径，叶片绕Y轴以角速度Ω转动，其动力方程参数为将式（8）代入动力平衡方程可得直叶片的动力平衡方程为

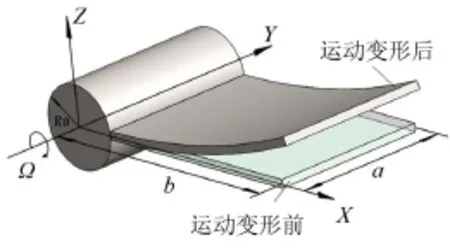
图2　直叶片悬臂板模型

2　相似关系

设几何相似关系为λ，λ为模型与原型的相似比，由相似原理知完全几何相似时

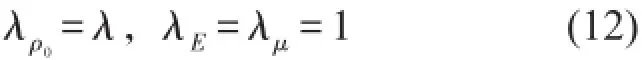
运用方程分析法，由式（9）、（10）、（11）可得相似关系式

为横向振型相似比；λΩ为转速相似比；λωd为动频率相似比。

由式（13）可知

3　过渡模型

由式（14）知，转速相似关系λΩ=1/λ，即模型叶片的转速是原型叶片转速倍，也就是模型越小，则要求转速越高，而高转速不仅会导致系统产生高阶振动而影响测量结果，而且也使得实验成本大大增加，故可考虑改变叶片动力相似模型中的转速相似关系，通过建立低转速的过渡相似模型来预测原型叶片的动力特性。

由叶片动频率满足［8］

式（15）中，ωd为动频率；ω为静态固有频率；B为动频系数；Ω为旋转角速度。

建立过渡相似模型对原型动频率进行预测，设过渡模型与原型相似关系为

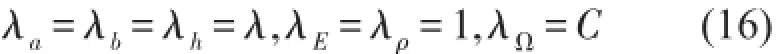
式（16）中，C为常数。

4　数值验证

选用原型与模型直板叶片的几何参数及转速如表1所示［9-11］，取模型与原型材料参数相同，材料参数如下：弹性模量E=104.8 GPa，密度ρ=4 428 kg/m3，泊松比μ=0.3。设完全几何相似相似比为λ=0.5。

表1　原型和模型参数

采用实体单元分别对原型和模型直板叶片进行有限元建模，通过数值仿真计算得到考虑动力柔化效应的原型与模型前5阶动频率及通过相似关系式（14）由模型动频率预测的原型动频率如表2所示。

表2　原型和模型动频率

由表2数值验证结果可知式（14）所得相似关系是准确、可靠的。

对原型直板叶片施加n=0～1 256 rad/s的转速（每隔157 rad/s为一个计算点），考虑动力柔化效应和不考虑动力柔化效应的各阶动频率如图3所示。

图3　各阶动频率对比

由文献［12］可知，建立过渡相似模型的可行性在于各阶动频系数B为常数，即动频率对于旋转角频率为线性关系。对于柔性叶片，由图3可知其动频率随转速的变化为非线性关系，故不能通过过渡模型预测原型的动力特性。由此，对于刚性叶片的模型试验，可通过过渡模型的方法在低转速下对高速旋转叶片进行模拟，而对于柔性叶片，试验中则应保证其转速的完全相似关系。

5　结语

运用相似原理，通过分析考虑动力柔化效应的直板叶片动力平衡方程，得到以下结论：

（1）考虑动力柔化的直板叶片动态固有频率相似比与转速相似比相同，是几何尺寸相似比的倒数；

（2）数值仿真结果验证了所建立相似关系是正确和有效的，并证明直板叶片的动力柔化效应对动频率的影响随转速增大而增大；

（3）数值仿真结果验证了对刚性叶片的模型试验可通过建立较低转速的过渡相似模型来避免试验模型高阶振动，对柔性叶片的模型试验则应采用转速完全相似的试验模型。

［1］郝燕平.叶轮机叶片结构相似性问题的理论研究［A］.中国航空学会第六届动力年会论文集［C］.南京，2006. CSAA06-P-084.

［2］罗忠，朱云鹏，陈晓兵，等.复合材料层合板相似模型的几何区间确定方法［J］.机械工程学报，2014，50（9）：58-64. ［3］陈小波，李静，陈健云.考虑离心刚化效应的旋转风力机叶片动力特性分析［J］.地震工程与工程振动，2009，29 （1）：117-122.

［4］Friedmann P P.Aeroelastic scaling for rotary-wing aircraft with applications［J］.Journal of Fluids and Structures，2004，19（5）:635-650.

［5］YCFung.Foundationsofsolidmechanics［M］. Englewood Cliffs，NJ:Prentice-Hall，1965.

［6］Yoo H H，Chung J.Dynamics of rectangular plates undergoingprescribedoverallmotion［J］.Journalof Sound and Vibration，2001，239（1）:123-137.

［7］Yoo H H，Kim S K.Free vibration analysis of rotating cantilever plates［J］.AIAA Journal，2002，40（11）:2188-2196.

［8］沈庆楼，刘湘一，贾忠湖，等.发动机叶片振动特性分析［J］.海军航空工程学院学报，2005，（04）：473-476.

［9］马辉，能海强，宋溶泽，等.基于变厚度壳单元的旋转叶片固有特性分析［J］.航空发动机，2013，39（5）：26-30.

［10］Qin Z Y，Yan S Z，Chu F L.Dynamic analysis of slender launching system connected by clamp band joint using harmonicbalancemethod［J］.JournalofPhysics: Conference Series，4 th Symposium on the Mechanics of Slender Structures，2013，448（1）:1-8.

［11］Qin Z Y，Yan S Z，Chu F L.Influence of clamp band joint on dynamic behavior of launching system in ascent flight ［J］.ProceedingsoftheInstitutionofMechanical Engineers，Part G:Journal of Aerospace Engineering，2014，228（1）:97-114.

［12］Yoo H H，Shin S H.Vibration analysis of rotating cantilever beams［J］.Journal of Sound and Vibration. 1998，212（5）:807-828.

Dynamic Similarity Relations of Straight Blades Considering Dynamic Softening Effects

ZHAO Xiao-yu1，HUANGHai1，QUTao2，GUOJian3，LUOZhong3
（1.AVIC ShenyangAero-engine Design Institute，Shenyang 110042，China；2.Air Force Representative Office of PLAin ShenyangArea，Shenyang 110031，China；3.School of Mechanical Engineering&Automation，Northeastern University，Shenyang 110819，China）

A method for dynamic similarity model design considering the dynamic softening effect was put forward. The dynamic equilibrium equations for rectangular plates were formulated based on the large displacement kinetic equations for moving plates.On this basis，combining with the kinetic characteristics of the straight blade，the dynamic equilibrium equation of the straight blade was established based on the flexural body assumption.Using the dynamic similarity principle，the dynamic similarity equation of the rotating straight blade was established.In order to avoid the high order vibration induced by over-high revolution speed，a method for establishing the transition model of the rotating straight blade was put forward.The applicability of the method was analyzed in the condition of rigid and flexible straight blades.Finally，the efficiency and correctness of the similarity relation were verified by numerical simulation.

vibration and wave；dynamic softening；rotating blade；experimental model；dynamical similarity；transition model

TH113.1

ADOI编码：10.3969/j.issn.1006-1335.2015.05.008

1006-1355（2015）05-0043-05

2015－01－06

国家重点基础研究发展计划（973计划）资助项目（2012CB026005）；教育部基本科研业务费专项资金资助项目（N130503001；N140301001）

赵晓宇（1980－），男，辽宁锦州市人，硕士，研究方向：整机动力学设计。

E-mail:rain65535@sina.com

罗忠（1978－）男，内蒙古集宁人，博士，主要研究方向：机械动力学与控制。

E-mail:zhluo@mail.neu.edu.cn