探讨指、对数图象交点问题
2015-08-18叶涛
叶涛
高中教材没有探讨函数[y=ax与y=logax]图象的交点问题,仅仅只是在同一坐标系中画了函数[y=12x与y=log12x]以及[y=2x与y=log2x]的图象. 这张图让很多同学都误以为:函数[y=ax(0
比如,函数[y=116x与y=log116x]有三个公共交点,其中有两个公共交点[N112,14,N214,12]关于直线[y=x]对称,还有一个交点落在直线[y=x]上.另外对于函数[y=1.1x]来说,由于其图象上的一点[2,1.21]在直线[y=x]的下方,因而它的图象与直线[y=x]相交且有两个交点,即:函数[y=1.1x与y=log1.1x]的图象有两个落在直线[y=x]上的交点. 由于函数[y=ax与][y=logax(a>0][且a≠1)]互为反函数,其图象关于直线[y=x]对称,可以通过讨论函数[y=ax]的图象与直线[y=x]的交点个数确定函数[y=ax与y=logax]图象交点的个数.
我们可以通过几何画板绘制出函数[y=ax(a>1)]的图象,不难发现当底数[a]较大时与直线[y=x]无交点;当底数[a]较小,非常接近1[a>1]时有两个交点;当[0
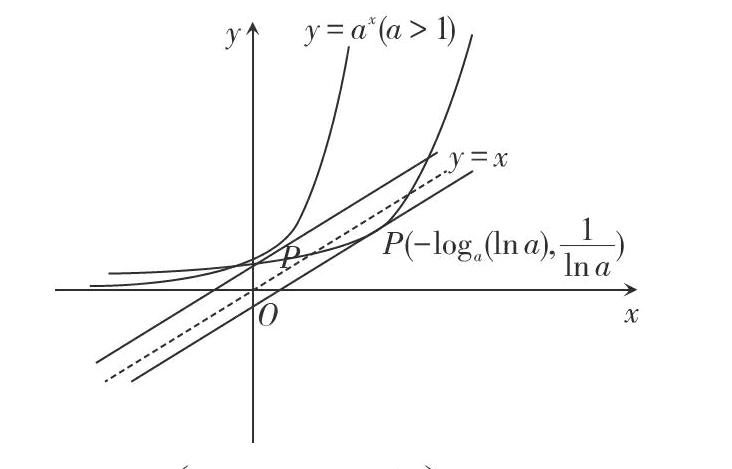
如下图在指数函数[y=ax(a>1)]的图象上,先求斜率为1的切线与[y=ax(a>1)]相切的切点[P]的坐标,根据切点[P]与直线[y=x]的相对位置确定函数[y=ax]的图象与直线[y=x]的交点情形,亦即:令[y=axlna=1]得,[x=-loga(lna).]
切点坐标[P-loga(lna),1lna],若点[P]在直线[y=x]上即[-loga(lna)=1lna得,a=e1e].
(1)当[a=e1e]时,函数[y=ax]的图象与直线[y=x]相切于点[P(e,e).]
(2)当[a>e1e]时,[lna>1e, ∴0<1lna 则有[loga1lna 此时切点[P-loga(lna),1lna]在直线[y=x]的上方,也即[y=ax(a>e1e)]的图象恒在直线[y=x]的上方,函数[y=ax]的图象与直线[y=x]无交点. (3)当[1 则有[loga1lna>logae],[∴-logalna>1lna]. 此时切点[P-loga(lna),1lna]在直线[y=x]的下方,也即[y=ax(1 由上述分析不难得到以下定理. 定理1 对于指数函数[y=ax(a>1)]的图象,当[a=e1e]时,其与直线[y=x]相切于点[P(e,e)];当[a>e1e]时,它恒在直线[y=x]的上方;当[1 由于函数[y=ax与y=logax(a>0且a≠1)]互为反函数,其图象关于直线[y=x]对称,因此有以下结论. 定理2 对于对数函数[y=logax(a>1)]的图象,当[a=e1e]时,其与直线[y=x]相切于点[P(e,e)];当[a>e1e]时,它恒在直线[y=x]的下方;当[1 定理3 对于函数[y=ax(a>1)与y=logax(a>1)]的图象,当[a=e1e]时,有且只有一个公共点;当[a>e1e]时,它们没有公共点;当[1 当[0 [练习] 1. 在[P(1,1),Q(1,2),M(2,3)和N(12,14)]四点中,函数[y=ax]的图象与其反函数的图象的公共点只可能是点( ) A. [P] B. [Q] C. [M] D. [N] 2. 下列结论中错误的是( ) A. 若点(2,3)在函数[y=ax]的图象上,则点(3,2)必在函数[y=logax]的图象上 B. 函数[y=ax]的图象必过点(0,1),就是说函数[y=logax]的图象必过点(1,0) C. 若点[m,n]既在函数[y=ax]的图象上,又在函数[y=logax]的图象上,则[m=n] D. 函数[y=logax]的图象与直线[y=x]不一定有交点 3. 对于问题“函数[f(x)=ax(a>1)]与其反函数[f-1(x)=logax]的图象有多少个公共点?”有如下观点:(1)当[a>1]时两函数图象没有公共点,只有当[0 请参考上述观点,并判断以下结论正确的是 (填写序号). ①当[a>e1e]时,函数[f(x)=ax(a>1)]的图象与直线[y=x]没有公共点 ②当[a>e1e]时,函数[f(x)=ax(a>1)]的图象与直线[y=x]有两个相异公共点 ③当[a=e1e]时,函数[f(x)=ax(a>1)]的图象与直线[y=x]没有公共点 ④当[a=e1e]时,函数[f(x)=ax(a>1)]的图象与直线[y=x]有惟一的公共点 ⑤当[1 ⑥当[1