几何画板在高中数学教学中的应用研究

孙喜宗

【摘 要】苏联著名数学家A.H.柯尔莫戈洛夫指出：“只要有可能，数学家总是尽力把他们正在研究的问题从几何上视觉化。”数学科学最重要的是抽象思维和形象思维的结合，但从人类数学思维系统的发展来说，形象思维是最早出现的，并在数学研究和教学中都起着重要的作用。很难想象，一个没有得到形象思维培养的人会有很高的抽象思维、理论思维的能力，同样，一个学生如果根本不具备数学想象力，要把数学学好那也是不可能的。基于此，从国外引进的教育软件几何画板以其学习入门容易和操作简单的优点及其强大的图形和图象功能、方便的动画功能被国内许多数学教师看好，并已成为制作中学数学课件的主要创作平台之一。那么，几何画板在高中数学教学中有哪些应用呢？本文从它在高中代数、解析几何、立体几何中的应用等方面加以研究。

【关键词】高中数学     几何面板     应用

一、几何面板在高中代数教学中的应用

华罗庚说：“数缺形少直观，形缺数难入微。”为了解决数形结合的问题，在有关函数的传统教学中多以教师手工绘图为主，但手工绘图有不精确、速度慢的弊端;应用几何画板快速直观地显示及变化功能则可以克服上述弊端，大大提高课堂效率，起到事半功倍的教学效果。

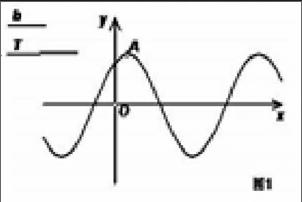
具体说来，可以用几何画板根据函数的解析式快速作出函数的图象。并可以在同一个坐标系中做出多个函数的图象，如在同一个直角坐标系中作出函数y=x2. y=x3和y=x1/2的图象，比较各图象的形状和位置，归纳幂函数的性质。还可以做出含有若干参数的函数图象，当参数变化时函数图象也相应地变化，如在讲函数y=Asin（ωx+φ）的图象时，传统教学只能将A、ω、φ代入有限个值，观察各种情况时的函数图象之间的关系;利用几何画板则可以以线段b、T的长度和A点到x轴的距离为参数作图（如图1），当拖动两条线段的某一端点（即改变两条线段的长度）时分别改变三角函数的相位和周期，拖动点A则改变其振幅 ，这样在教学时既快速灵活，又不失一般性。

二、几何面板在高中解析几何教学中的应用

平面解析几何是用代数方法来研究几何问题的一门数学学科，它研究的主要问题，即它的基本思想和基本方法是：根据已知条件，选择适当的坐标系，借助形和数的对应关系，求出表示平面曲线的方程，把形的问题转化为数来研究;再通过方程，研究平面曲线的性质，把数的研究转化为形来讨论。而曲线中各几何量受各种因素的影响而变化，导致点、线按不同的方式作运动，曲线和方程的对应关系比较抽象，学生不易理解，显而易见，展示几何图形变形与运动的整体过程在解析几何教学中是非常重要的。这样，几何画板又以其极强的运算功能和图形图象功能在解析几何的教与学中大显身手。如它能做出各种形式的方程（普通方程、参数方程、极坐标方程）的曲线;能对动态的对象进行“追踪”，并显示该对象的“轨迹”;能通过拖动某一对象（如点、线）观察整个图形的变化来研究两个或两个以上曲线的位置关系。

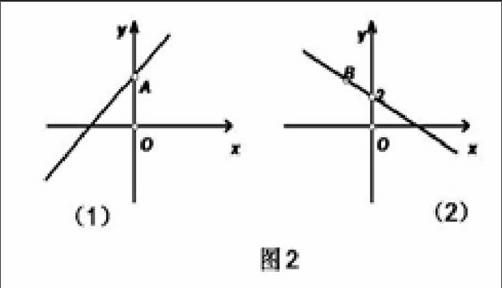
具体地说，比如在讲平行直线系y=x+b或中心直线系y=kx+2时，如图2所示，分别拖动图（1）中的点A和图（2）中的点B时，可以相应地看到一组斜率为1的平行直线和过定点（0，2）的一组直线（不包括y轴）。

三、几何面板在高中立体几何教学中的应用

初学立体几何时，大多数学生不具备丰富的空间想象能力及较强的平面与空间图形的转化能力，主要原因在于人们是依靠对二维平面图形的直观来感知和想象三维空间图形的，而二维平面图形不可能成为三维空间图形的真实写照，平面上绘出的立体图形受其视角的影响，难于综观全局，其空间形式具有很大的抽象性。如两条互相垂直的直线不一定画成交角为直角的两条直线;正方体的各面不能都画成正方形等。这样一来，学生不得不根据歪曲真象的图形去想象真实情况，这便给学生认识立体几何图形增加了困难。而应用几何画板将图形动起来，就可以使图形中各元素之间的位置关系和度量关系惟妙惟肖，使学生从各个不同的角度去观察图形。这样，不仅可以帮助学生理解和接受立体几何知识，还可以让学生的想象力和创造力得到充分发挥。

如在讲《锥体的体积》时，可以演示将三棱柱分割成三个体积相等的三棱锥，这样既避免了学生空洞的想象而难以理解，又锻炼了学生用分割几何体的方法解决问题的能力;在用祖恒原理推导球的体积时，运用动画和轨迹功能当拖动点O时，平行于桌面的平面截球和柱锥所得截面也相应地变动，直观美丽的画面使学生在学得知识的同时，给人以美的感受，创建了一个轻松、乐学的氛围。

综上所述，使用几何画板进行数学教学，通过具体的感性的信息呈现，能给学生留下更为深刻的印象，使学生不是把数学作为单纯的知识去理解，而是能够更有实感地去把握它。这样，既能激发学生的情感、培养学生的兴趣，又能大大地提高课堂效率。endprint