一种新的基于稀疏表示的宽带信号DOA估计方法

赵永红张林让 刘 楠 解 虎

（西安电子科技大学雷达信号处理国家重点实验室 西安 710071）

一种新的基于稀疏表示的宽带信号DOA估计方法

赵永红*张林让 刘 楠 解 虎

（西安电子科技大学雷达信号处理国家重点实验室 西安 710071）

该文提出一种基于稀疏表示的宽带信号波达方向（DOA）估计方法，解决稀疏表示方法在宽带信号DOA估计中由于基矩阵维数过大而使算法存储量和重构计算量大的问题。用单一频点的基矩阵代替频率和角度联合构建的基矩阵，使基矩阵的列数仅相当于一个频点处冗余基矩阵的列数，大大降低了稀疏重构方法的存储量和计算量。该方法首先对各频点的频域数据进行聚焦处理，将不同频率的数据堆叠到参考频率上并建立参考频率处的基矩阵，然后建立聚焦后的稀疏表示模型进行DOA估计，并采用奇异值分解进一步降低算法的运算量，最后给出残差门限的选择方法。该算法不仅适用于非相关信号，也可直接处理相关信号而不需要任何的去相关运算，且具有高的检测概率和估计精度，仿真实验和分析验证了该方法的有效性。

波达方向估计；稀疏表示；宽带信号；相关信号

1 引言

阵列信号波达方向（DOA）的估计一直以来是个热点问题，主要解决的问题是在噪声背景下实现对信源的检测和角度的估计。人们对 DOA估计的研究经历了很长的一段发展历程，在此期间也产生了大量的算法，例如经典的Capon方法［1］和子空间类方法［2，3］。近几年来，学者们基于信号空间分布的稀疏性，将稀疏重构的思想用于 DOA估计中，提出了很多基于稀疏表示的DOA估计方法［4-7］，这些方法与经典的谱估计方法相比，具有很高的估计精度和分辨能力。

上述研究方法最初都是基于窄带信号，针对宽带信号，一般都采用分频处理模型，得到每个子频带的接收数据，然后再采用某种方法对各频带上的数据进行融合处理并给出最终的 DOA估计结果。文献［8］基于稀疏重构的思想提出了宽带L1-SVD方法，该方法存在两个问题，一方面，该方法基矩阵的大小由宽带信号子频带个数和角度划分个数共同决定，当频带个数较大时，该算法的存储量和重构计算量将会非常大。另一方面，该方法最终的DOA估计结果是各个子频带估计结果的平均值，这种处理过程仅仅独立地利用了每个子频带的稀疏性，并没有有效利用不同频带的联合稀疏性。文献［9］提出了L1-SVD方法的扩展方法，对宽带信号实现了各个子频带的联合估计，并采用奇异值分解降低了算法的运算量，但是该方法基矩阵的维数依然很大，并没有解决L1-SVD方法存储量和重构计算量的问题。文献［10］基于协方差矩阵拟合提出了 W-SpSF方法，该方法实现了各个子频带协方差矩阵的联合估计，但该方法基矩阵的维数仍然取决于子频带的个数和角度划分的个数，因此也存在存储量和重构计算量大的问题。文献［11］引入空间频率的概念，将频率和角度2维空间降为空间角1维空间，这种方法虽然降低了算法的存储量和重构计算量，但对宽带信号而言，该算法很难实现各个频带之间的联合估计。

针对以上问题，本文利用聚焦方法的思想，提出了一种新的基于稀疏表示的宽带信号 DOA估计方法。该方法将各个子频带的频域数据聚焦到参考频率点上，从而得到相同频率下的频域数据，然后再利用聚焦后的数据进行稀疏重构，这时的基矩阵不再依赖于子频带的个数及各个子频带的频点，仅仅与参考频率和角度的划分方式有关。因此，所提方法不但实现了各个子频带的联合估计，而且降低了基矩阵的维数，从而实现存储量和重构计算量的降低。

2 信号模型

2.1 宽带信号的数学模型

假设空间远场存在K个宽带信号，中心频率均为f，信号带宽均为B，以角度入射到由N个阵元组成的均匀线阵上，阵元间距为中心频率的半波长。采用分频处理模型对宽带信号进行处理，将其划分为J个子频带，则第i个子频带的信号的模型［12］为

ηk为第k个信号的功率， δ（·）表示单位冲激响应函数，为噪声信号，假设服从高斯分布，满足且与目标信号不相关，I为单位矩阵，是i个子频带的阵列流形矩阵，c是信号的传播速度，是阵元间距。

在实际应用场合中，宽带信号源大量存在，因此宽带信号 DOA估计是值得深入研究的。经典的基于信号子空间类的宽带 DOA估计方法主要分为两类：非相干子空间法（ISM）［13］和相干子空间法（CSM）［14，15］。ISM 将宽带信号分解为若干个窄带信号，然后对每个窄带信号进行独立的信号子空间处理，最后将每个窄带信号估计结果的均值作为最终的估计结果。CSM将不同频点上的信号子空间聚焦到参考频率上，对聚焦后得到的参考频率处协方差矩阵进行子空间处理得到最终的估计结果。从ISM和CSM的处理过程可以看出，ISM和CSM都存在子空间类方法的不足，即需要估计信源的个数，而且ISM方法不能直接处理相关信号。为了克服子空间类方法的不足，学者们提出了大量基于稀疏表示的宽带信号DOA估计方法［16，17］。

2.2 基于稀疏表示的DOA估计模型

由于空间信源的个数相对于整个空域来说是有限的，因而导致信源在角度空间的稀疏性。稀疏表示的主要思想是将阵列流形矩阵过完备化，从而使得目标信号矢量稀疏化。假设集合覆盖所有可能的目标入射方向，Q是空间角度划分个数，且满足Q ＞＞ N，以此构造超完备基矩阵在基矩阵的表示下，可以得到第i个子频带用于DOA估计的稀疏模型为

最终的 DOA估计结果由各个子频带稀疏重构结果的平均获得，这种方法的处理过程类似于ISM，并没有将不同子频带的信息联合起来，实现频带间的联合估计，而且不同子频带的基矩阵也不同，这样增加了算法的存储量和重构计算量。为此，本文利用聚焦的思想，不仅实现频带间的联合估计而且降低算法的存储量和重构计算量。

3 多频带联合DOA估计方法

3.1基于聚焦变换的宽带信号DOA估计模型

现有的基于稀疏表示的宽带信号 DOA估计方法，不管是频带间的独立估计还是频带间的联合估计，大都存在冗余基矩阵存储量大和稀疏重构计算量大的问题。本文算法将不同频率的子频带信号映射到参考频率上，只需建立参考频率点处的冗余字典，从而减小了存储量，另外该算法对频域快拍数没有要求。对阵列接收的一帧数据进行DFT变换，得到的频域数据可以表示为

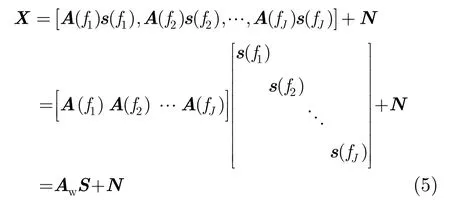
假设宽带信号的参考频率为 f0，则对于第 i子频带，需要构造该频带上对应的聚焦矩阵使得

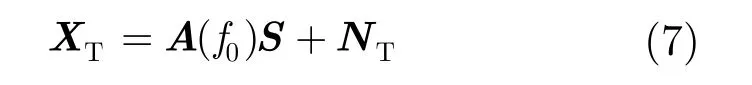
3.2 基于稀疏表示的宽带信号DOA估计方法

传统的基于聚焦矩阵的宽带信号 DOA估计方法是将不同频点的阵列数据映射到参考频率上，得到聚焦后单一频点处的协方差矩阵，再采用子空间类算法实现角度估计。而本文方法中，不需要计算协方差矩阵，并且对频域快拍数没有要求。将式（7）中的阵列流形矩阵 A（ f0）进行过完备化，可得到聚焦后用于DOA估计的稀疏模型：

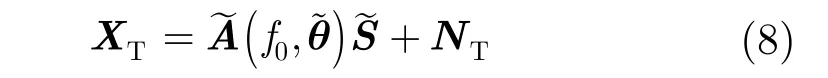
从而提取聚焦后频域数据 XT的信号子空间为

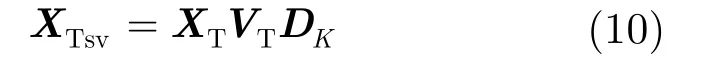
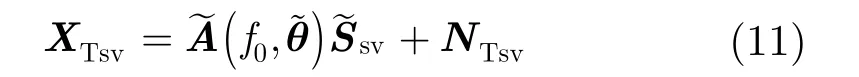
容易知道，系数矩阵S~sv的每一列具有相同的行稀疏结构，因此可以实现联合估计。将式（11）的求解转化为式（12）的优化形式：

从式（12）可以看出，我们已经成功地将目标角度θ的参数估计问题转化为稀疏向量矩阵S~sv的谱估计问题。式（12）的求解是一个优化问题，通过简单的调整可将其转化为二阶锥规划的形式：

3.3 门限的选取

式（12）中，残差门限β是一个非常重要的参数，用来平衡信号稀疏性和噪声的影响。由式（11）可以得到

再将式（14）代入式（12）的不等约束中，得到

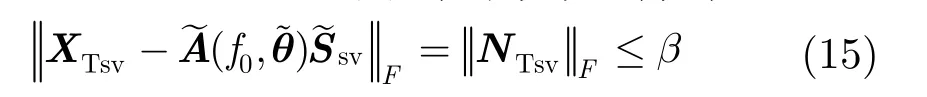
β的取值必须使式（15）以高概率成立。假设各个子频带的噪声服从高斯分布且互相独立，满足

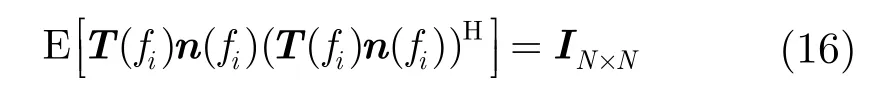
根据式（16）可以得到聚焦后的噪声矩阵 NT=

的每一列独立同分布且满足均值为 0，方差为1的高斯分布，根据文献［8］可以得到

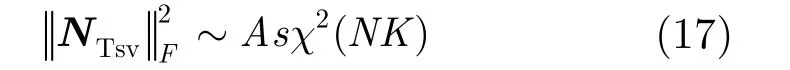
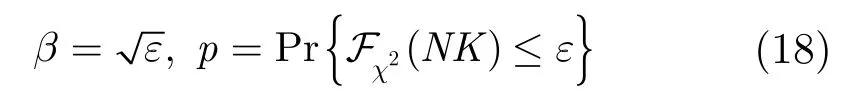
4 性能分析

本文算法的主要目的是降低稀疏表示方法在宽带信号分频处理过程中存储量和重构计算量大的问题，为了说明所提算法大大降低了基矩阵的存储量和算法重构的计算量，现将该算法的存储量和重构计算量与L1-SVD和文献［9］的方法进行比较，3种算法的求解均采用内点法。假设角度划分的个数为Q，阵元个数为N，后两种算法采用 SVD降维后重构数据的列数均等于目标的个数K， 3种算法基矩阵的存储量和算法重构的计算量列于表1中。

表1 算法存储量和重构计算量对比结果

表1表明相对于L1-SVD和文献［9］算法，本文算法的存储量和重构计算量均大大降低，在阵元个数和目标个数给定的情况下，存储量和计算复杂度的大小都与子频带的个数无关，而仅仅与角度划分的个数有关。L1-SVD算法的存储量和重构计算量随子频带个数的增加而线性增加，文献［9］算法的存储量也随子频带个数线性增加，而重构计算量按指数倍增加。

为了进一步分析本文算法的性能，我们采用仿真数据进行分析。设天线阵列为均匀线阵，由16个相同的全向阵元组成，阵元间距为宽带信号中心频率的半波长，宽带信号的中心频率为100 Hz，带宽为中心频率的40%。初始角度的获得由波束形成给出，信号的传播速度为 c= 340 m/s 。仿真实验中以第1个频率点为参考频点进行聚焦，除实验3外，其它实验将宽带信号划分为33个子频带，所有实验的频域快拍数为1。

实验 1假设空间远场存在两个等功率宽带信号，信噪比为6 dB，一个信号固定在 θ1= 0°，另一个信号的角度为 θ2= θ1+Δθ ，其中角度间隔 Δθ =1°～ 15°，步长为1°。θ2在每个角度方向分别进行1000次独立的蒙特卡洛实验，得到重构以后能够正确检测两个目标的概率随第2个目标角度的变化关系，其中图1是非相关信号，图2是相关信号。从图中可以看出，本文算法不仅适用于非相关信号，而且也适用于相关信号，并且两种情况下，在角度间隔较小时，当文献［9］算法不能检测时，本文算法仍能以一定的概率正确估计两个信号。这里我们设定检测概率的定义为：在每次实验中，若估计所得角度与真实角度差的绝对值均小于等于1°，则定义该次实验为一次正确检测，否则认为检测失败。

实验 2设定两个等功率目标的来波方向分别为 -3 0°和10°，将其信噪比进行变化，变化范围为0～15 dB，变化间隔为1 dB。每个信噪比下进行1000次独立的蒙特卡洛实验，得到重构以后的均方根误差（RMSE）随信噪比的变化曲线，其中图3是非相关信号，图4是相关信号。从图中可以看出，不管是非相关信号还是相关信号，本文算法的均方根误差均明显低于文献［9］算法、L1-SVD算法和传统的CSM方法，并且更接近克拉美罗界，说明在相同信噪比下，本文算法的估计性能优于另外3种算法。这里均方根误差的定义为其中，H 为在 1000次独立的蒙特卡洛实验中的总次数，K表示目标个数，表示在目标有效估计的第h次的第k个目标的估计角度， θk为第k个目标的真实角度。

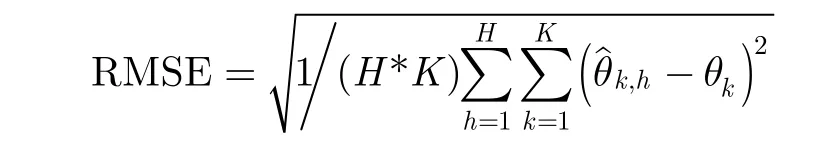
实验 3设定两个等功率目标的来波方向分别为 -3 0°和10°，信噪比为6 dB，但是将子频带的个数进行变化，变化范围为10～100，变化间隔为10。每个子频带个数下进行 1000次独立的蒙特卡洛实验，得到重构以后的均方根误差随子频带个数的变化曲线，其中图5是非相关信号，图6是相关信号。从图中可以看出，不管是相关信号还是非相关信号，在相同子频带个数下本文算法的均方根误差均明显小于文献［9］算法、L1-SVD算法和传统的CSM方法，并且更接近克拉美罗界，说明在相同子频带个数下本文算法的估计精度高于文献［9］算法、L1-SVD算法和传统的CSM方法。均方根误差的定义和实验2相同。

图1 检测概率随角度差的变化曲线（非相关信号）

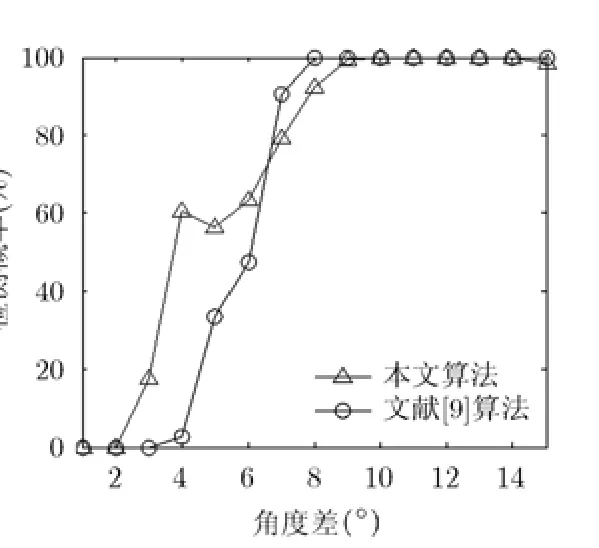
图2 检测概率随角度差 的变化曲线（相关信号）

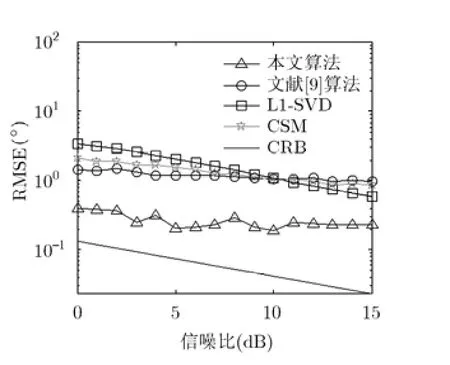
图3 RMSE随信噪比的 变化曲线（非相关信号）

图4 RMSE随信噪比的变化曲线（相关信号）

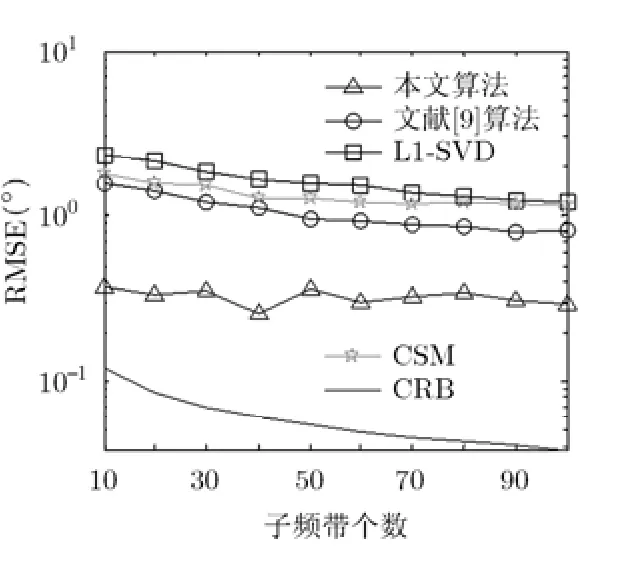
图5 RMSE随子频带个数 的变化曲线（非相关信号）

图6 RMSE随子频带个数 的变化曲线（相关信号）

实验 4本实验主要考察门限选取对 DOA估计结果的影响。假设空间远场存在两个等功率宽带信号，信噪比为10 dB。图7给出了目标角度分别为0°和30°时利用本文算法所得的稀疏空域谱。从图中可以看出本文算法能够对两个目标进行有效的估计。图8给出了目标角度分别为0°和5°时利用本文算法所得的空域谱。从图中可以看出，在角度间隔较小时，采用理论门限有可能出现伪峰现象，通过调整门限可以达到抑制伪峰的目的，从而提高本文算法DOA估计的稳健性。

实验 5本实验主要考察预估角误差对本文算法的影响。假设空间远场存在一宽带信号源，信噪比为15 dB，信号源的真实角度为θ，预估角度为，预估角误差的取值范围为：0 °～ 12°，每个预估角误差下进行 1000次独立的蒙特卡洛实验，得到重构以后的均方根误差随预估角误差的变化曲线如图9所示。从图中可以看出，当预估角误差小于瑞利限时，均方根误差很小（均小于1°），但当预估角误差大于瑞利限时，随着预估角误差的增大，均方根误差急剧增大，这说明初始角度的取值（预估角误差小于瑞利限时）对算法的影响不大。

图7 空域谱（目标角度为0°和30°）

图8 空域谱（目标角度为0°和5°）

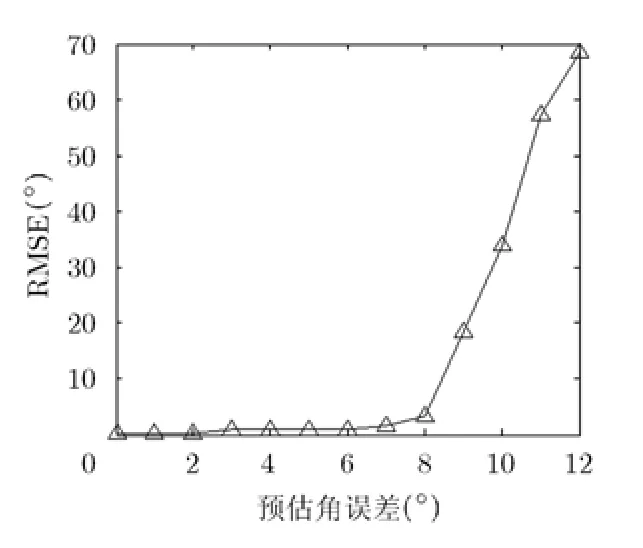
图9 RMSE随预估角误差的变化曲线

5 结论

本文利用聚焦的思想，提出了一种基于稀疏表示的宽带信号 DOA估计方法。一方面，该方法的存储量和重构计算量均与子频带个数无关，而取决于阵元个数，角度划分个数以及目标个数，解决了稀疏表示方法在宽带信号处理中存储量和重构计算量大的问题；另一方面，该方法实现了频带间的联合估计。另外，对于残差约束门限的选取，本文给出了一种选择依据。该方法不仅可以处理非相关信号，也可直接处理相关信号而不需要任何的预处理，仿真结果表明，该方法具有高的检测概率和估计精度。

［1］ Rübsamen Michael and Pesavento Marius. Maximally robust capon beamformer［J］. IEEE Transactions on Signal Processing， 2014， 62（7）: 1834-1849.

［2］ Rangarao K V and Venkatanarasimhan S. Gold-MUSIC: a variation on MUSIC to accurately determine peaks of the spectrum［J］. IEEE Transactions on Antennas and Propagation， 2013， 61（4）: 2263-2268.

［3］ Steinwandt J， Roemer F， and Haardt M. Performance analysis of ESPRIT-type algorithms for non-circular sources［C］. IEEE International Conference on Acoustics，Speech and Signal Processing （ICASSP）， Vancouver， BC，2013: 3986-3990.

［4］ Hu N， Ye Z， Xu D， et al.. A sparse recovery algorithm for DOA estimation using weighted subspace fitting［J］. Signal Processing， 2012， 92（10）: 2566-2570.

［5］ Yin Ji-hao and Chen Tian-qi. Direction-of-arrival estimation using a sparse representation of array covariance vectors［J］. IEEE Transactions on Signal Processing， 2011， 59（9）: 4489-4493.

［6］ 沈志博， 董春曦， 黄龙， 等. 基于压缩感知的宽频段二维DOA估计算法［J］. 电子与信息学报， 2014， 36（12）: 2935-2941. Shen Zhi-bo， Dong Chun-xi， Huang Long， et al.. Broadband 2-D DOA estimation based on compressed sensing［J］. Journal of Electronics & Information Technology， 2014， 36（12）: 2935-2941.

［7］ 林波， 张增辉， 朱炬波. 基于压缩感知的DOA估计稀疏化模型与性能分析［J］. 电子与信息学报， 2014， 36（3）: 589-594. Lin Bo， Zhang Zeng-hui， and Zhu Ju-bo. Sparsity model and performance analysis of DOA estimation with compressive sensing［J］. Journal of Electronics & Information Technology，2014， 36（3）: 589-594.

［8］ Malioutov D M， Çetin M， and Willsky A S. A sparse signal reconstruction perspective for source localization with sensor arrays［J］. IEEE Transactions on Signal Processing， 2005，53（8）: 3010-3022.

［9］ Liu Zi-cheng， Wang Xue-lei， Zhao Guang-hui， et al.. Wideband DOA estimation based on sparse representation-an extension of L1-SVD in wideband cases［C］. IEEE International Conference on Signal Processing， Communication and Computing （ICSPCC）， Kunming， 2013: 1-4.

［10］ He Zhen-qing， Shi Zhi-ping， Huang Lei， et al.. Underdetermined DOA estimation for wideband signals using robust sparse covariance fitting［J］. IEEE Signal Processing Letters， 2015， 22（4）: 435-439.

［11］ 李鹏飞， 张旻， 钟子发. 基于空频域稀疏表示的宽频段DOA估计［J］. 电子与信息学报， 2012， 34（2）: 404-409. Li Peng-fei， Zhang Min， and Zhong Zi-fa. Broadband DOA estimation based on sparse representation in spatial frequency domain［J］. Journal of Electronics & Information Technology， 2012， 34（2）: 404-409.

［12］ Zhao Guang-hui， Liu Zi-cheng， Lin Jie， et al.. Wideband DOA estimation based on sparse representation in 2-D frequency domain［J］. IEEE Sensors Journal， 2015， 15（1）: 227-233.

［13］ Han K and Nehorai A. Wideband Gaussian source processing using a linear nested array［J］. IEEE Signal Processing Letters，2013， 20（11）: 1110-1113.

［14］ Kumar D S， Hinduja I S， and Mani V V. DOA estimation of IR-UWB signals using coherent signal processing［C］. IEEE 10th International Colloquium on Signal Processing & Its Application （CSPA）， Malaysia， 2014: 288-291.

［15］ Hung H and Kaveh M. Focusing matrices for coherent signal-subspace processing［J］. IEEE Transactions on Acoustics，Speech， and Signal Processing， 1988， 36（8）: 1272-1281.

［16］ Hu N， Xu X， and Ye Zhong-fu. DOA estimation for wideband signals based on sparse signal reconstruction using prolate spheroidal wave functions［J］. Signal Processing， 2014， 96（5）: 395-400.

［17］ Liu Zhang-meng and Huang Zhi-tao. Direction-of-arrival estimation of wideband signals via covariance matrix sparse representation［J］. IEEE Transactions on Signal Processing，2011， 59（9）: 4256-4270.

赵永红： 女，1989年生，博士生，研究方向为阵列信号处理.

张林让： 男，1966年生，教授，博士生导师，研究方向为阵列信号处理、雷达系统仿真.

刘 楠： 男，1981年生，副教授，研究方向为MIMO雷达、网络化雷达协同探测及抗干扰.

解 虎： 男，1987年生，博士生，研究方向为阵列信号处理、空时二维自适应处理.

A Novel Method of DOA Estimation for Wideband Signals Based on Sparse Representation

Zhao Yong-hong Zhang Lin-rang Liu Nan Xie Hu
（National Laboratory of Radar Signal Processing， Xidian University， Xi’an 710071， China）

A novel wideband signals Direction-Of-Arrival （DOA） estimation method based on sparse representation is proposed. This algorithm can reduce the storage and calculation of the traditional sparse representation methods in wideband signals process， which is caused by the large dimension of base matrix. The over-complete dictionary is constructed by using one-frequency to replace the 2D combination of frequency and angle. The column number of constructed dictionary only equals to that of single-frequency redundant dictionary. The proposed method first adopts focused thought to stack the different frequency data to the reference frequency and founds the redundant dictionary with a single frequency. Then， a sparse recovery model is established to obtain the DOA estimations，which are coming from following the focus process. At the same time， the Singular Value Decomposition （SVD） is used to summarize each frequency to reduce computation burden further. Finally， an automatic selection criterion for the regularization parameter involved in the proposed approach is introduced. The proposed algorithm can effectively distinguish the correlative signals without any decorrelation processing， and it has higher accuracy and detection possibility. The experiment results indicate that the proposed method is effective to estimate the DOA of wideband signals.

Direction-Of-Arrival （DOA） estimation； Sparse representation； Wideband signal； Correlative signal

s: The National Foundation for Key Laboratory（914XXX1002）； The Fundamental Research Fund for the Central Universities of China （JB140213）

TN957.51

A

1009-5896（2015）12-2935-06

10.11999/JEIT150423

2015-04-13；改回日期：2015-07-03；网络出版：2015-08-28

*通信作者：赵永红 Zhaoyh_2014@163.com

国家重点实验室基金（914XXX1002）和中央高校基本科研业务费（JB140213）资助课题