基于块稀疏贝叶斯模型的ISAR成像方法

吴称光 邓 彬 苏伍各 王宏强秦玉亮

（国防科技大学电子科学与工程学院 长沙 410073）

基于块稀疏贝叶斯模型的ISAR成像方法

吴称光 邓 彬 苏伍各 王宏强*秦玉亮

（国防科技大学电子科学与工程学院 长沙 410073）

传统ISAR稀疏成像主要针对独立散射点散射系数的重构问题，然而实际情况下目标散射点之间并不是独立存在的，而是以区域或块的形式存在，在该情形下利用常用的稀疏重构算法并不能完全地刻画块状目标的真实结构，因此该文考虑采用块稀疏重构算法进行目标散射系数重建。基于块稀疏贝叶斯模型和变分推理的重构方法（VBGS），包含了稀疏贝叶斯学习（SBL）方法中参数学习的优点，其利用分层的先验分布来表征未知信号的稀疏块状信息，因而相对于现有的恢复算法能够更好地重建块稀疏信号。该方法基于变分贝叶斯推理原理，根据观测量能自动地估计信号未知参数，而无需人工参数设置。针对稀疏块状目标，该文结合压缩感知（CS）理论将VBGS方法用于ISAR成像，仿真实验成像结果表明该方法优于传统的成像结果，适合于具有块状结构的ISAR目标成像。

逆合成孔径雷达；块稀疏模型；压缩感知；块稀疏贝叶斯模型和变分推理

1 引言

近年来随着稀疏重构方法和压缩感知（Compress Sensing， CS）理论的发展，其在ISAR成像中得到成功的应用，相比较传统的基于傅里叶变换的ISAR成像方法，稀疏ISAR成像方法可以用比Nyquist采样定理要求的少得多的采样数据来精确地重建目标像［1，2］。现存的稀疏雷达成像方法大都将目标考虑为点目标，即非0的目标散射系数离散的分布在目标的成像区域内［3-7］。

然而在实际情况下，ISAR目标具有一些块状结构特性，即这些非0的目标散射系数是连续的位于目标成像场景中。本文所讨论的块成像方法，主要针对散射分布具有块结构的目标，如具有复杂结构的飞机目标、卫星目标等，这些目标均具有块状的特性。因在微波频段一般认为目标具有少数散射中心，因此实际目标只要呈现出散射中心多并且大都连续即可适用于块成像方法。另外在太赫兹频段，实际目标呈现粗糙特性，在这种情形下也适用于块成像方法。在块成像场景中采用常用的稀疏恢复方法如基于平滑 l0准则方法（Smoothed l0norm，SL0）［8］，稀疏贝叶斯学习（Sparse Bayesian Learning，SBL）［9］方法，方差成分扩张压缩（Expansion-Compression Variance-component based method，ExCoV）［5，10］方法等并不能完全地重建真实目标的结构信息，而块稀疏重构方法在具有块结构特性的稀疏信号恢复中能够较好地估计出源信号。

2 块稀疏ISAR成像模型

ISAR利用目标与雷达的相对运动获得高的方位分辨率，目标与雷达之间的相对运动包含简单的直线运动和复杂的曲线运动，通常可分解为平动和转动两个分量。经平动补偿处理之后，任意运动形式的目标都可以归结为转台目标，即目标相对于雷达只有旋转运动。根据 GTD理论，在高频极限情况下雷达目标总的电磁散射可认为是某些局部位置上的电磁散射所合成，即雷达回波可由目标少数强散射点所构成，因此本文采用稀疏表示方法来表征雷达目标信号的回波。设S为测得的 ISARM ×N维回波数据矩阵，并令δ为目标成像区域离散化之后的 2维K × L散射率分布矩阵，将按列堆叠后的矢量化表示形式记为并考虑在成像过程中所引入的噪声，记为n，根据文献［3，5］可得ISAR成像的稀疏表示模型为

其中φ为根据雷达成像模型获得的一欠完备的字典，即MN ≪ KL，相对于雷达成像场景，未知矢量x包含了少量雷达目标散射点，即x包含了小部分的非零元素，大部分的元素等于0或接近于0。

在稀疏信号表示中，为使在变换域上用尽量少的原子来准确地表示原始信号（即x含有尽量少的非零元素），可用式（2）表示为

其中β为噪声方差，τ为正则化参数。

当前常用的稀疏恢复模型，都是将稀疏惩罚项强加于向量x的各个元素上，并假设这些元素之间相互独立。近年来块稀疏恢复模型（即将稀疏惩罚项强加于向量x的一簇元素中）的出现概括了传统的稀疏模型，块稀疏恢复模型通过将信号中相关的元素聚类起来，考虑了信号中的块结构特性，并考虑信号分量之间的相关性。通过与传统的强加于独立元素的稀疏模型，块稀疏模型能够去除掉不相关的分量，从而获得较高的信号恢复性能。

在块稀疏恢复中最常见的结构是块结构（block structure）或称为簇群结构（group structure），即矢量x包含了g个块，每个块 xi包含了 di个信号分量，如式（4）所示。

3 贝叶斯块稀疏模型及变分贝叶斯参数估计方法

3.1 贝叶斯块稀疏信号全概率模型

假设一信号先验独立于块之间，即信号先验可表示为［17，18］

其中z为一向量包含了所有的 zi，则在群稀疏先验中，稀疏性度量通过先验概率 p（ xi|zi）来表征。当考虑多变量的高斯模型均值为 0，方差为 ziIdi时有则 xi的边缘概率分布可表示

为

本文中考虑信号模型（广义逆高斯分布模型）［18］

其中 Kλi为第2类修正的Bessel函数，其分布矩为

则由式（6）可得广义的双曲线分布为

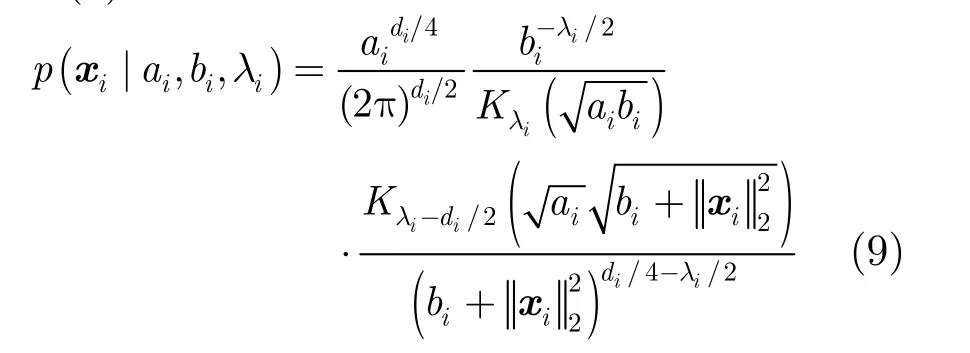
在广义的双曲线分布中，通过变化参数 ai，bi，λi值，可得一系列的先验分布函数［18］。

假设独立的高斯噪声满足均值为0方差为 β-1，则关于观测信号的条件概率分布可表示为同时对参数β赋予共轭的伽马先验结合分层次的先验概率式（7）和式（9），则联合概率分布可表示为

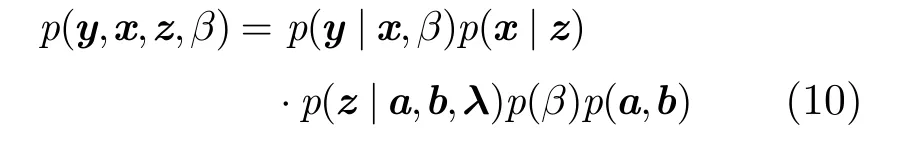
3.2 变分贝叶斯参数估计方法

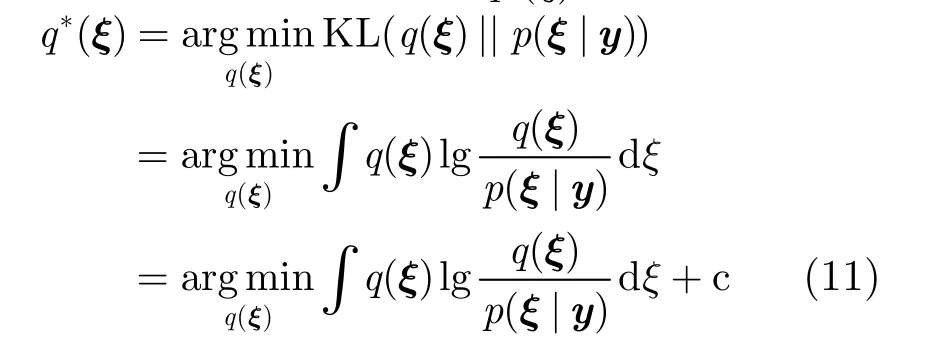
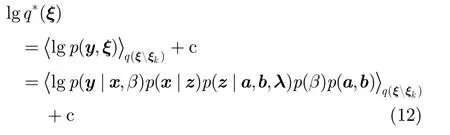
（1）结合联合概率分布由式（12）可得参数x的近似后验概率为多元高斯分布，其中，

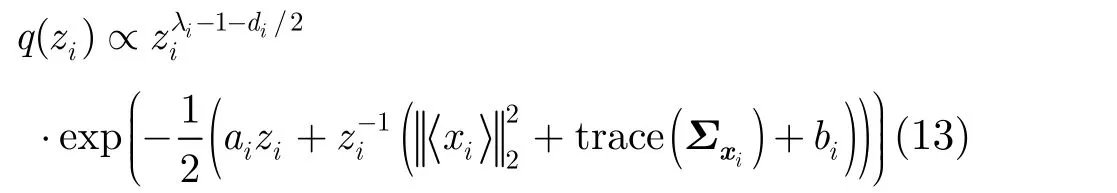
其中 ∑xi表示矩阵 ∑x对应于第i个块的子矩阵。则由式（8）可得的后验估计为

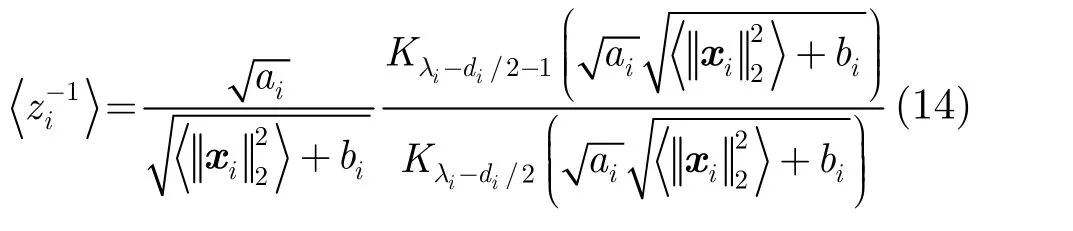
（3）超参数 ai与 bi的估计不再详述。在特定的分布情况下估计超参数，如当先验为McKay’s Bessel函数分布时，为自由参数。采用伽马分布作为混合概率密度函数，对于相应的超参数 ai，选择共轭的伽马分布与 θa分别为形状参数和尺度参数，则可得参数ai的后验概率为相应的更新规则为其中可由式（8）和式（14）获得。当为多变量的Student’s-t分布时，同样选择与 bi共轭的伽马分布则其后验概率分布同样也为伽马分布其均值为

（4）根据伽马先验，β的估计可用其均值来进行近似表示，即其中

综上所述，图1给出了分层的群稀疏贝叶斯联合概率模型中各个参数之间的关系图。贝叶斯推理过程就是根据各个变量之间的概率分布，利用变分贝叶斯参数估计方法从已知变量中估计未知参数的过程。

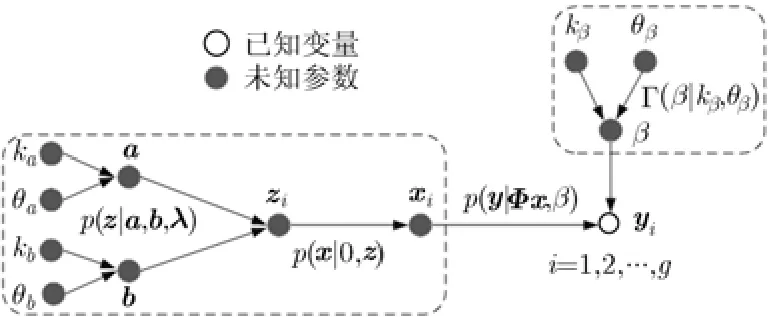
图1 群稀疏贝叶斯模型变量关系图

4 仿真实验结果

为分析比较基于VBGS的块目标ISAR成像算法的性能，本节通过MATLAB仿真来验证该方法，并将仿真结果与传统的ISAR成像方法极坐标格式算法（Polar Format Algorithm， PFA）和卷积逆投影算法（Convolution Back Projection Algorithm，CBPA），稀疏重构方法ExCoV和常用的块稀疏重构方法Group-Lasso进行比较，在采用块稀疏重构算法时，均采用均匀划分块的方式。在仿真实验中均加入SNR = 10 dB的高斯白噪声。本文在比较过程中用PFA和CBPA方法时采用全部回波数据，而采用CS方法做ISAR成像时，选择随机矩阵作为采样矩阵，采样方式同文献［5］。实验中雷达均发射线性调频信号，载频10 GHz，带宽1 GHz，采样点数为 512，设目标总转角 θmax为5°，转动期间录取的回波数为 512，并且设雷达与目标的距离满足远场条件，目标散射中心散射强度均设为 1，成像区域大小为2.2 m × 2.2 m，在建立稀疏词典时，距离向和方位向的离散化间隔均设置为 0.1 m。同文献［5］，根据式（1）即可获得目标各个姿态下的回波数据。

实验1中主要进行了简单块目标结构散射系数重构，无噪声情况下的块状目标场景如图2（a）所示，目标包含63个散射点。图2（b）和图2（c）为采用PFA和CBPA方法得到的ISAR像，采用这两种方法时，均使用了雷达回波的全部测量数据，从图中可看出该方法不能精确的重建目标像，旁瓣比较严重，但仍能准确地表达目标的形状信息。图2（d）为采用ExCoV方法得到的重建目标像，该方法能够较为精确地估计出目标散射点位置，但出现了一些虚假点目标的位置。图2（e）为采用Group-Lasso方法重建得到的目标像，Group-Lasso方法是基于Lasso方法的块稀疏重构算法，该方法可精确地表征目标的块信息结构，但该方法在重建目标像时，需要设置人工参数，并受噪声性能影响较大，从图中可看出其ISAR目标像周围分布着较多的虚假目标点。图2（f）为VBGS方法得到的ISAR像，VBGS方法同ExCoV都属于无人工参数设置的重构算法，该方法得到的成像结果无论从成像清晰度及抗噪能力上均优于以上算法，因而可适用于含块状信息的ISAR目标成像。

为更好地说明VBGS方法能更好的重建块状目标的ISAR像，在实验2中，设置了多个块目标构成复杂块目标结构，即将目标的宽度加大，并将目标块数设置为4，目标总共包含72个散射点，如图3（a）所示，仿真实验条件及算法参数设置同实验1。图3（b）， 3（c）为采用PFA与CBPA方法得到的成像结果，其均有高旁瓣低分辨率的特性。当设置多个块目标时，ExCoV方法不能准确地重构目标像，出现大量的目标散射点失真，其结果如图3（d）所示。图3（e）示出了Group-Lasso方法的成像结果，从结果图中可看出，受噪声及块设置的影响，其完全不能重建目标形状信息。图3（f）给出了本文方法的成像结果，从该结果中可看出VBGS方法能精确估计出ISAR目标块状信息，并具有较优良的分辨率，从而说明该方法适用于具有多个块状目标结构的ISAR成像。

前两个实验在设置目标散射点系数值时，都将其设置为1，然而在实际情况下，雷达目标的散射点强度大都不相同，因此在实验3中，在实验2的基础上，将点目标的散射系数值在0～1之间进行随机选取，如图4（a）所示。仿真实验条件及算法参数设置同前两个实验，从图4的成像结果综合比较，只有VBGS方法的成像结果较为精确地估计出目标散射系数值，并能正确重建出目标结构形状，因此VBGS方法适合于实际情形下的ISAR成像。

图2 实验1简单块目标结构 ISAR 成像结果

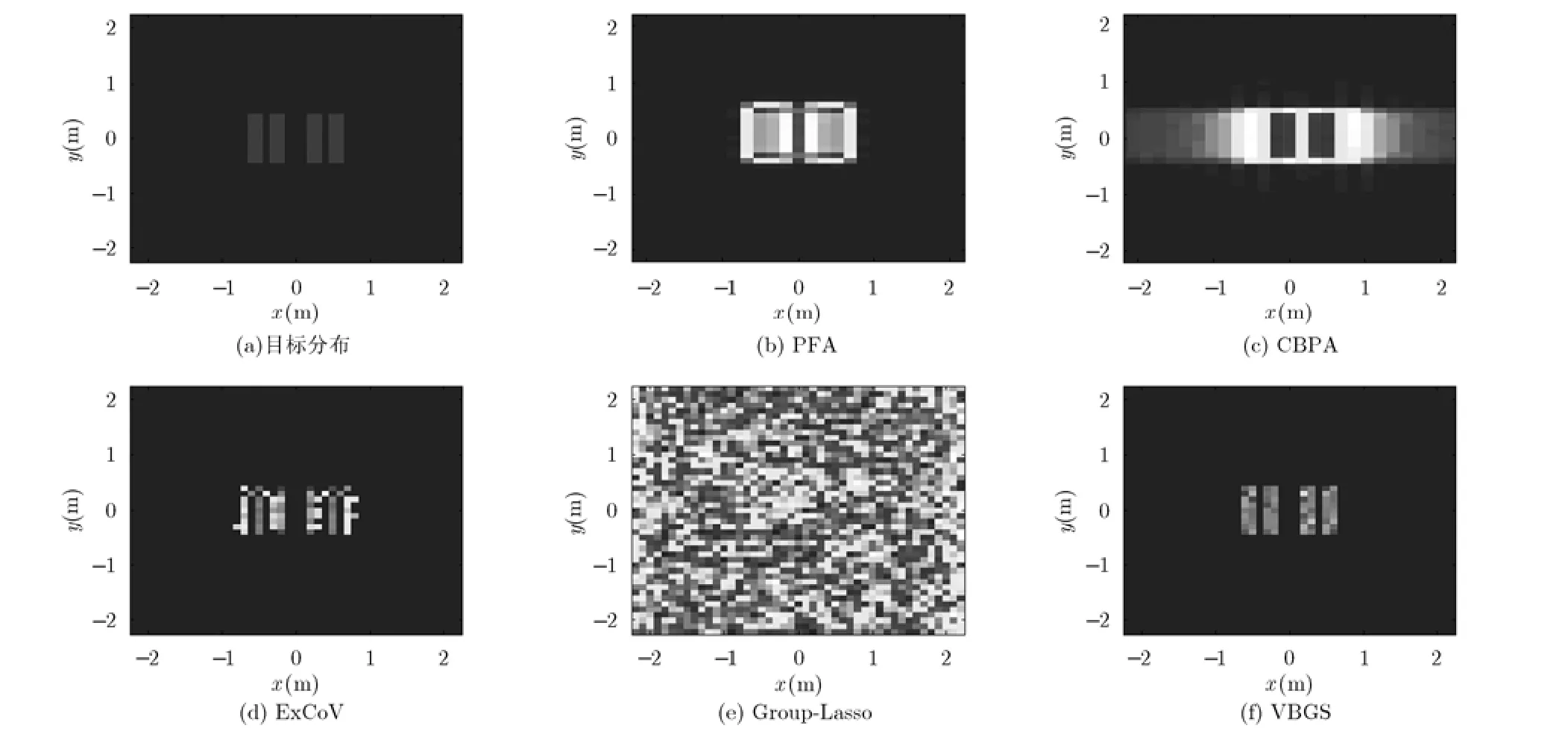
图3 实验2复杂块目标结构 ISAR 成像结果

5 结束语

在一些特定条件下的ISAR目标成像中，目标散射系数具有块状的结构信息，即目标的非0散射点连续的分布在同一分布区域中，在这种情形下，传统的成像结果不能重建出目标的块状信息。本文探讨了一种在贝叶斯框架下的块稀疏重构算法，该算法通过设置分层的信号先验模型，采用变分贝叶斯推理的方法来估计信号参数和模型中的超参数，无需设置人工参数，能够自动地估计出目标信号参数。仿真实验中将该方法用于块状结构的ISAR目标成像，与传统成像方法相比较，能够较好地重建目标ISAR像。该研究成果对于实际情况中含块状信息的ISAR目标高分辨成像提供了一定的理论依据，对块状目标ISAR高分辨成像算法的研究具有一定的意义。下一步工作，在低信噪比条件下，在获得块状目标实测数据的背景下，考虑将该方法应用块状目标ISAR成像，以进一步验证该方法的成像性能。

图4 实验3不同散射系数下 ISAR 成像结果

［1］ Candes E J and Wakin M B. An introduction to compressive sampling［J］. IEEE Signal Processing Magazine， 2008， 25（2）: 21-30.

［2］ Zhang Xiao-hua， Bai Ting， Meng Hong-yun， et al.. Compressive sensing based ISAR imaging via the combination of the sparsity and nonlocal total variation［J］. IEEE Geoscience and Remote Sensing Letters， 2014， 11（5）: 990-994.

［3］ Rao Wei， Li Gang， and Wang Xi-qin. Parametric sparse representation method for SAR imaging of rotating targets［J］. IEEE Transactions on Aerospace and Electronic Systems，2014， 50（2）: 910-919.

［4］ 吴敏， 邢孟道， 张磊. 基于压缩感知的二维联合超分辨 ISAR成像算法［J］. 电子与信息学报， 2014， 36（1）: 187-193. Wu Min， Xing Meng-dao， and Zhang Lei. Two dimensional joint super-resolution ISAR imaging algorithm based on compressive sensing［J］. Journal of Electronics & Information Technology， 2014， 36（1）: 187-193.

［5］ 苏伍各， 王宏强， 邓彬， 等. 基于方差成分扩张压缩的稀疏贝叶斯 ISAR 成像方法［J］. 电子与信息学报， 2014， 36（7）: 1525-1531. Su Wu-ge， Wang Hong-qiang， Deng Bing， et al.. Sparse Bayesian representation of the ISAR imaging method based on ExCoV［J］. Journal of Electronics & Information Technology， 2014， 36（7）: 1525-1531.

［6］ Yang Jun-gang， Huang Xiao-tao， Thompson J， et al.. Compressed sensing radar imaging with compensation of observation position error［J］. IEEE Transactions on Geoscience and Remote Sensing， 2014， 52（8）: 4608-4620.

［7］ Liu Zhen， You Peng， Wei Xi-zhang， et al.. Dynamic ISAR imaging of maneuvering targets based on sequential SL0［J］. IEEE Geoscience and Remote Sensing Letters， 2013， 10（5）: 1041-1045.

［8］ Figueiredo M A T， Nowak R D， and Wright S J. Gradient projection for sparse reconstruction: application to compressed sensing and other inverse problems［J］. IEEE Journal of Selected Topics in Signal Processing， 2007， 1（4）: 586-597.

［9］ Wipf D P and Rao B. Sparse Bayesian learning for basis selection［J］. IEEE Transactions on Signal Processing， 2004，52（8）: 2153-2164.

［10］ Qiu Kun and Aleksandar D. Variance-component based sparse signal reconstruction and model selection［J］. IEEE Transactions on Signal Processing， 2010， 58（6）: 2935-2952.

［11］ Eldar Y C and Mishali M. Robust recovery of signals from a structured union of subspaces［J］. IEEE Transactions on Information Theory， 2009， 55（11）: 5302-5316.

［12］ Meier L， Van De Geer S， and Buhlmann P. The group lasso for logistic regression［J］. Journal of the Royal Statistical Society: Series B （Statistical Methodology）， 2008， 70（1）: 53-71.

［13］ Stojnic M. L2/L1-optimization in block-sparse compressed sensing and its strong thresholds［J］. IEEE Journal of Selected Topics in Signal Processing， 2010， 4（2）: 350-357.

［14］ Eldar Y C， Kuppinger P， and Bolcskei H. Block-sparse signals:Uncertainty relations and efficient recovery［J］. IEEE Transactions on Signal Processing， 2010， 58（6）: 3042-3054.

［15］ Zhao Li-fan， Wang Lu， Bi Guo-an， et al.. An autofocus technique for high resolution inverse synthetic aperture radar imagery［J］. IEEE Transactions on Geoscience and Remote Sensing， 2014， 52（10）: 6392-6403.

［16］ Liu Hong-chao， Jiu Bo， Liu Hong-wei， et al.. Super-resolution ISAR imaging based on sparse Bayesian learning［J］. IEEE Transactions on Geoscience and Remote Sensing， 2014， 52（8）: 5005-5013.

［17］ Zhang Zhi-ling and Rao B D. Extension of SBL algorithms for the recovery of block sparse signals with intra-block correlation［J］. IEEE Transactions on Signal Processing， 2013，61（8）: 2009-2015.

［18］ Babacan S D， Nakajima S， and Do M N. Bayesian group sparse modeling and variational inference［J］. IEEE Transactions on Signal Processing， 2014， 62（11）: 2906-2921.

吴称光： 男，1985年生，博士生，研究方向为雷达成像技术与运动检测技术.

邓 彬： 男，1981年生，讲师，研究方向为合成孔径雷达、太赫兹雷达.

苏伍各： 男，1986年生，博士生，研究方向为雷达成像技术及稀疏表示方法.

王宏强： 男，1970年生，研究员，博士生导师，研究方向为雷达信号处理、压缩感知、太赫兹雷达技术等.

秦玉亮： 男，1980年生，副研究员，研究方向为雷达信号处理.

ISAR Imaging Method Based on the Bayesian Group-sparse Modeling

Wu Cheng-guang Deng Bin Su Wu-ge Wang Hong-qiang Qin Yu-liang
（School of Electronic Science and Engineering， National University of Defense Technology， Changsha 410073， China）

The traditional sparse ISAR imaging method mainly considers the recovery of coefficients on individual scatters. However， in the practice situation， the target scatters presented by blocks or groups do not emerge on individual. In this case， the usual sparse recover algorithm can not depict the shape of real target， thus， the group-sparse recover approaches are adopted to reconstruct the coefficients of target scatters. The recovery method based on the Bayesian Group-Sparse modeling and Variational inference （VBGS） uses a hierarchical construction of a general signal prior to model the group sparse signals and contain the merit of Sparse Bayesian Learning （SBL）on parameters learning， as a result， it can reconstruct the group sparse signal better than the usual recover algorithm. The VBGS method uses the variational Bayesian inference approach to estimate the parameters of the unknown signal automatically and does not require the parameter-tuning procedures. Considering the sparse group target， this paper combines the Compress Sensing （CS） theory and the VBGS method to reconstruct the ISAR image. The result of experiments show that the proposed method can improve the imaging accuracy compared with traditional algorithm， and can fit to reconstruct the image of ISAR target which has group structure.

Inverse SAR （ISAR）； Group sparse model； Compress Sensing （CS）； Bayesian Group-Sparse modeling and Variational inference （VBGS）

s: The National Natural Science Foundation of China （61171133）； The National Natural Science Foundation for Young Scientists of China （61101182， 61302148）

TN957.52

A

1009-5896（2015）12-2941-07

10.11999/JEIT141624

2014-12-18；改回日期：2015-10-19；网络出版：2015-11-01

王宏强 oliverwhq1970@gmail.com

国家自然科学基金（61171133），国家自然科学青年基金（61101182， 61302148）