锅筒截面瞬态温度场的导热正反问题耦合解法

李　斌，　陈　丰，　史良宵

(华北电力大学 能源动力与机械工程学院，河北保定 071003)



锅筒截面瞬态温度场的导热正反问题耦合解法

李斌，陈丰，史良宵

(华北电力大学 能源动力与机械工程学院，河北保定 071003)

针对外壁受热的增压锅炉锅筒，提出了求解其截面瞬态温度场的导热正反问题耦合解法.根据锅筒外壁是否受热，将其外壁划分为受热和不受热2个区域.对于不受热区域，沿外壁周向布置热电偶，根据实际测量所得温度，利用导热反问题解法求解该区域的温度场；对于受热区域，利用导热正问题解法求解其温度场；对于耦合边界区域，将不受热区域反问题解法得到的交接边界处温度赋值给受热区域正问题解法作为已知边界条件，从而实现正反问题耦合，得到整个锅筒截面的瞬态温度场.利用Ansys软件对锅炉冷态启动过程中锅筒的温度场进行了计算，并与正反问题耦合解法的计算结果进行了对比.结果表明：正反问题耦合解法具有较高的精度，在复杂边界条件下具有很好的适应性，能够满足工程应用的需要.

锅炉锅筒； 温度场； 导热反问题； 导热正问题； 正反问题耦合解法

锅筒是锅炉最大的厚壁承压部件，在启、停过程中及变负荷运行时，承受着由于温度分布不均匀而产生的热应力和由内部压力引起的机械应力的共同作用.频繁的应力变化会引起锅筒的疲劳寿命损耗.因此，对锅筒应力进行在线监测，在锅炉工作过程中控制锅筒应力在允许范围内，进而减小锅筒的疲劳寿命损耗，这对锅炉的安全运行具有重要意义[1-5].

温度场计算是锅筒应力计算和疲劳寿命分析的基础，精度将直接影响疲劳寿命分析的结果.传统的锅筒温度场求解根据锅筒内部换热条件，在已知结构参数、热物性参数、初始条件和边界条件的前提下，通过导热微分方程得到温度场.这种方法又称为导热问题的直接解法或正问题解法[6-7].该方法根据边界条件的不同，可适用于复杂边界条件情况(不同边界条件分别作用或者几种边界条件同时作用).由于锅筒内部流动和换热过程复杂，内壁换热的边界条件难以准确确定，锅筒内壁与饱和水和饱合水蒸气的对流传热系数hw和hs通常采用经验数据，从而导致温度场计算存在误差.

为了弥补导热正问题解法的不足，有学者提出了温度场计算的导热反问题解法[8-10].其思路是在锅筒的外壁选定适当的位置布置热电偶，然后根据热电偶测得的温度值，采用控制容积法，建立控制容积的能量守衡方程，进而求解其瞬态温度场.Murio[11]根据有限差分法采用反问题解法求解一维导热反问题；Duda和Taler采用有限差分法将反问题解法运用到形状简单的控制体，求解其二维导热反问题，然后又采用控制容积法和反问题解法求解复杂形状控制体的多维导热反问题；Taler等[12]采用反问题解法通过控制容积法的理论对多维导热反问题进行求解，并通过一维和二维导热反问题进行精度验证；Taler等[13]采用反问题解法求解瞬态温度场并应用于电厂实际在线监测系统.

导热反问题解法适用于外壁不受热锅筒的温度场求解，可以减小由于内壁传热系数采用经验公式计算带来的误差.但对于外壁受热的情况，如增压锅炉锅筒[14]，其上部区域近似绝热，但其下部外壁部分边界受炉内火焰辐射换热，且为了维持微正压，夹层处热空气与锅筒外壁进行对流换热，换热情况复杂，炉内高温环境下无法布置热电偶，这种情况不再适宜采用导热反问题解法.

为此，笔者提出了导热正反问题耦合解法，将导热正问题解法与反问题解法相结合，求解复杂边界条件下某增压锅炉锅筒截面的瞬态温度场，并利用Ansys软件对该方法的计算精度进行了验证.

1　模型的建立

图1为某增压锅炉的锅筒，其中锅筒内径r1=0.65 m，锅筒外径r5=0.74 m.锅筒内壁换热条件为上部空间的汽和下部空间的水与锅筒对流换热.外壁不同区域的换热条件不同，图1中上部白色区域外壁为绝热条件，下部灰色区域为炉内火焰与锅筒外壁的直接辐射换热，两端阴影部分为夹层处热空气与锅筒外壁的对流换热.

根据锅筒外壁的换热条件，将锅筒划分为2部分(见图2)：外壁不受热区域(采用导热反问题解法求解)和外壁受热区域(采用导热正问题解法求解).

图1　锅筒截面简化模型

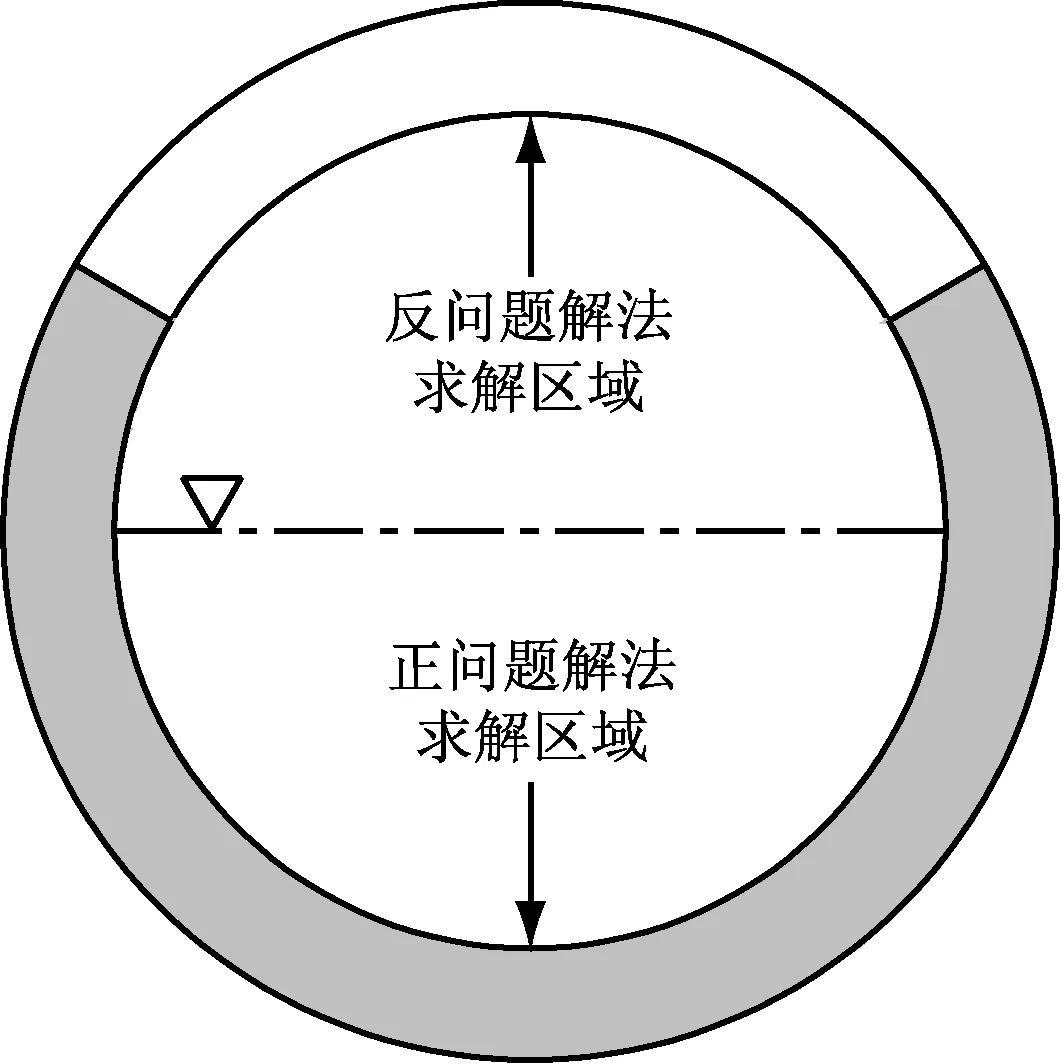
图2　锅筒截面求解区域划分示意图

由于锅筒上部白色区域外壁绝热，可以在其边界上布置热电偶，通过测得的外壁温度值，采用导热反问题解法求得该区域的温度场.下部灰色区域根据其内外壁边界条件和初始条件采用正问题解法求解导热微分方程，得到其温度场.两区域交接边界处采用边界耦合的方式，将反问题解法求得的两侧耦合边界的温度值作为已知的第一类边界条件带入正问题解法，实现整个温度场的求解.

根据正问题解法和反问题解法的需要，整个锅筒截面划分的网格如图3所示，其中S1和S2表示耦合边界，其余数字表示节点编号.

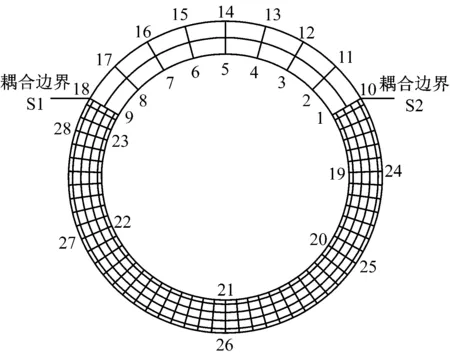
图3　锅筒截面网格示意图

2　温度场计算

2.1反问题解法

如图4所示，在锅筒外壁节点11～节点17处布置热电偶.

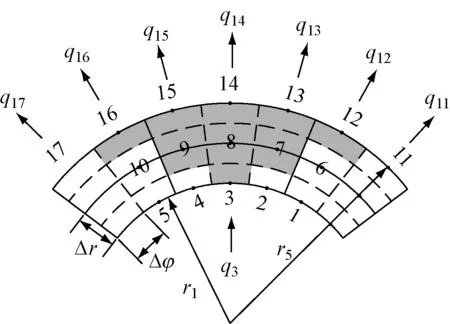
图4　反问题解法局部网格示意图

根据热电偶测得的外壁温度值，考虑到外壁存在一定的散热量，对于锅筒外壁每个节点所代表的控制容积，采用热平衡法和傅里叶定律列出各节点的能量守恒方程.外层节点13～节点15的能量守恒方程如下：

(1)

(2)

(3)

式中：c为材料的比热容，J/(kg·K)；ρ为材料密度，kg/m3；λ为材料导热系数，W/(m·K)；Δφ为控制容积角度变化量，rad；Δr为控制容积径向长度变化量，m；ti为节点i的温度，℃；qi为节点i的热流密度，W/m2.

根据式(1)～式(3)可以求解出中间层节点7～节点9的温度：

(4)

(5)

(6)

其中，α为热扩散率(α=λ/ρc),m2/s.

同理，根据中间层节点8的能量守恒方程得到内层节点3的温度：

(7)

由此通过外层节点的温度，逐次反推，求解得到内层节点的温度.同理改变不同外层节点位置，可得到整个内层节点的温度，从而得到锅筒截面反问题解法求解区域的瞬态温度场.

2.2正问题解法

根据锅筒内部换热条件，在已知结构参数、热物性参数、初始条件和边界条件的前提下，采用Simpler算法[2]求解导热微分方程，从而得到其温度场.

区域离散采用内节点法，290个节点分别位于188个子区域的中心，此时子区域即为控制容积.图5为正问题解法的网格划分示意图.

导热微分方程为

(8)

边界条件如下：

图5　正问题解法网格划分示意图

绝热边界

(9)

内壁边界

(10)

(11)

夹层对流

(12)

辐射换热

(13)

初始温度为

(14)

式中：q为热流密度，W/m2，炉内火焰与锅筒内壁换热处近似为第二类边界条件；hj为夹层外壁处对流传热系数，W/(m2·K)；tf为夹层外壁流体温度，℃;τ为时间,s;τ为时间，s;t0为初始温度,℃;t∞为流体的饱和温度,℃.

边界条件的处理如下：当边界条件为第二、第三类边界时，采用附加源项法对边界进行处理，即把由第二、第三类边界条件所规定的引入或者导出计算区域的热量作为与边界相邻的控制容积的当量源项，有利于统一模式处理边界条件.

最后采用交替方向线迭代及块修正的方法求解离散方程，得到整个求解区域的温度场.

2.3正反问题耦合解法

结合边界条件的不同，分别采用正问题解法和反问题解法对不同离散区域进行单独的温度场求解.

首先根据已知的反问题解法求解区域外壁的温度值(热电偶测温)，采用反问题解法求解该区域的温度场.两区域交接边界处(耦合边界S1和S2)采用正反问题耦合解法，将反问题解法求得的交接边界处的温度值作为正问题解法的已知条件(第一类边界条件)，然后通过插值的方式赋值给正问题解法求解区域，并将其作为已知边界条件，这样就完成了2个求解区域的温度传递.然后在已知结构参数、热物性参数、初始条件和其他边界条件的前提下，求解得到正问题解法求解区域的温度场.

当求解结束后，再将正问题解法求解得到的边界温度重新带回，进行迭代计算，直到输入与输出偏差在允许范围内，迭代计算结束，至此将温度场联系起来耦合求解，得到整个锅筒截面的瞬态温度场，计算流程如图6所示.

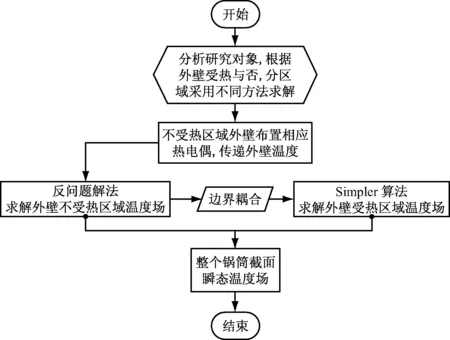
图6　计算流程图

3　正反问题耦合解法验证

为了验证正反问题耦合解法求解锅筒温度场的准确性，利用Ansys软件对该方法进行验证.

首先，利用Ansys软件对锅炉冷态启动过程中锅筒的温度场进行计算.如图7所示，计算时模型沿锅筒径向划分为5个节点，沿圆周方向划分为72个节点.锅筒边界条件的取值如下：q=50 000 W/m2，hw=1 000 W/(m2·K),hs=2 000 W/(m2·K)，hj=142 W/(m2·K),tf=127 ℃，t0=70 ℃.锅筒内流体的饱和温度随时间的变化关系如下：

(15)

然后，将利用Ansys软件求解得到的启动过程各时刻对应反问题解法求解区域的锅筒外壁温度作为该区域的已知条件，正问题解法求解区域采用的初始条件、边界条件等与Ansys软件计算时相同，重新应用本文方法计算锅筒启动过程的温度场.将2种方法的计算结果进行对比，从而验证正反问题耦合解法的正确性.

图7　Ansys软件中划分的网格示意图

3.1节点温度验证

根据不同边界条件，对锅筒中若干个具有代表性的节点(见图3)温度进行分析验证，对比分析正反问题耦合解法和Ansys软件2种方法的计算结果，温度随时间的变化如图8～图14所示.

图8给出了内壁节点5处2种方法计算结果的对比.该节点位于汽空间的锅筒内壁，即反问题解法求解区域.因为反问题解法需要已知外壁温度，所以将Ansys软件计算得到的外壁温度带入反问题解法，求解得到内壁温度，再与Ansys软件计算所得内壁温度进行对比分析.由图8可以看出，2种方法计算结果的吻合度很高.

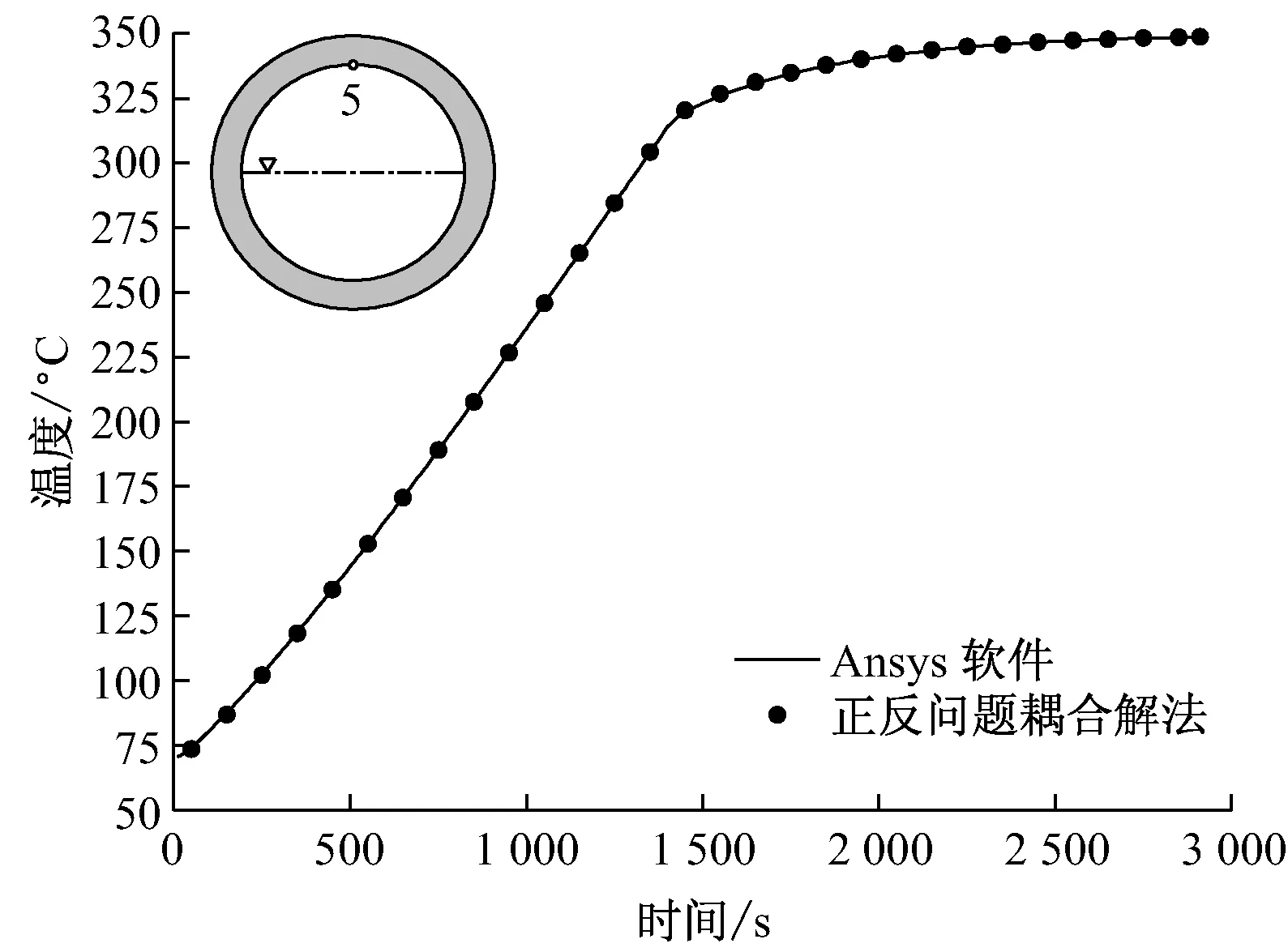
图8　节点5处温度的对比

图9给出了节点19和节点24处2种方法计算结果的对比.这2个节点位于汽水交接边界处，由于汽水混合，加之饱合水蒸气和饱合水与锅筒内壁的传热系数相差很大，换热复杂，造成该处附近点波动较大，温差也较大，3 000 s时内外壁温差很小，温度趋于均匀.

图10给出了节点20和节点25处2种方法计算结果的对比.这2个节点分别位于锅筒内水空间的内外壁处.整个过程中温度随时间的变化率比汽空间处小，与图9相比，图10中的换热强度较小，到3 000 s时内外壁温差较大.

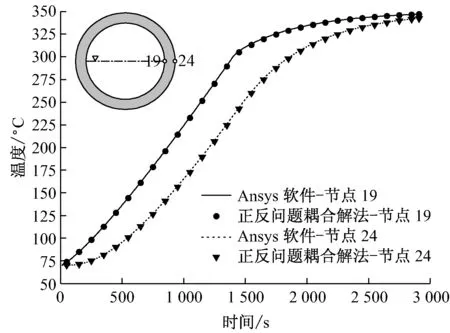
图9　节点19和节点24处温度的对比

图10　节点20和节点25处温度的对比

节点21和节点26处由于外壁受到炉内辐射换热的影响，相对常规电站锅炉的锅筒而言，外壁温度高，外壁向内壁换热.在开始阶段，内外壁温度随时间的变化率基本一致，当饱和水温度不变时，该处外壁温度继续升高，而内壁温度则变化较小(见图11)，导致内外壁温差逐渐增大，产生较大的热应力.

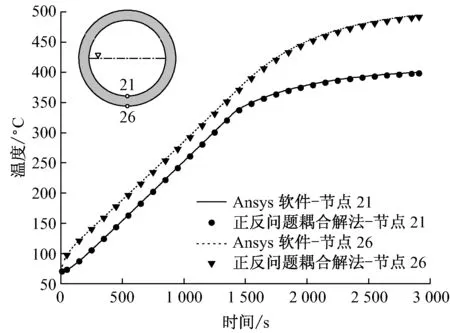
图11　节点21和节点26处温度的对比

图12给出了节点22和节点27处2种方法计算结果的对比.这2个节点分别位于正问题解法求解区域的夹层对流换热处的内外壁.由于夹层处外壁流体温度比锅筒内水的温度先高后低，所以造成该处内外壁温度相对于外层绝热区域外壁温度先高后低，同时内外壁温差最后也比绝热区域大.

图12　节点22和节点27处温度的对比

节点23和节点28分别位于正问题解法求解区域的汽空间内外壁处.相对于图10中水空间处的节点温度而言，由于上部饱和水蒸气与锅筒内壁的传热系数大，所以曲线斜率大，节点的温度变化更快；同时内外壁温差比水空间处大；到达稳定状态时，该区域内外壁温差较小，温度分布均匀(见图13).

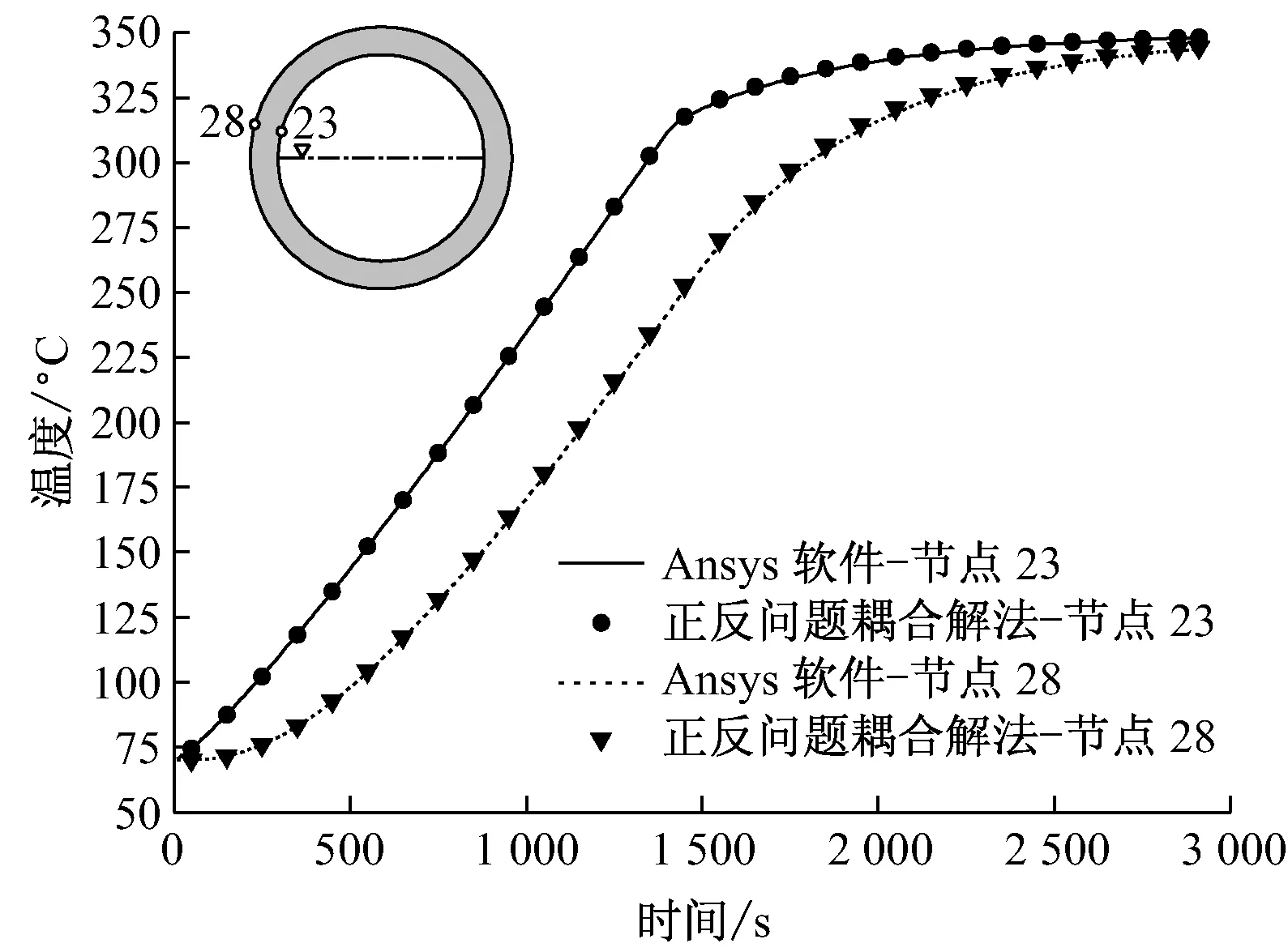
图13　节点23和节点28处温度的对比

图14给出了耦合边界节点1和节点10处温度的对比.耦合边界将反问题解法求解得到的边界温度作为已知边界赋值给正问题解法，求解完后再将边界温度反代回去，编制程序反复迭代，得到精确解.该处温度的变化与上部汽空间区域(见图13)一致.由图14可以看出，2种方法的计算结果吻合得很好.

由图8～图14还可以看出，2种方法在不同区域的求解结果吻合度都很高，说明所提出的正反问题耦合解法具有较高的精度.

3.2锅筒截面瞬态温度场的分布

采用正反问题耦合解法求解锅筒截面的瞬态温度场分布，不同时间截面瞬态温度场的分布如图15所示.

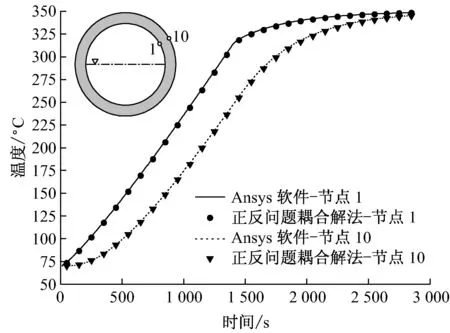
图14　节点1和节点10处温度的对比

图15(a)给出了τ=500 s时锅筒截面的等温线.此时下部热流作用时间较短，锅筒截面上下部温差相对较小，整个截面温度分布较均匀，下部内外壁温差也较小.

图15(b)给出了τ=1 000 s时锅筒截面的等温线.此时由于下部热流作用时间较长，影响范围增大，下部空间内壁温度高于上部空间，同时内外壁温差增大，上下部温差逐渐增大，热应力也相应增大.

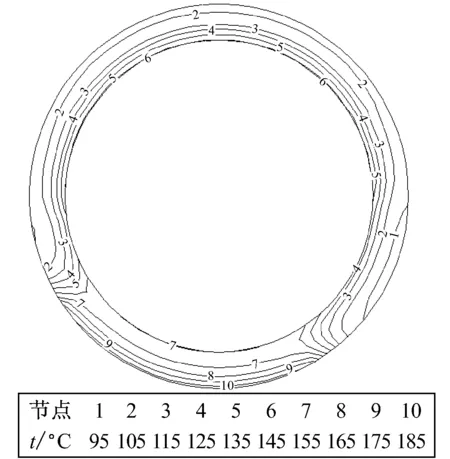
(a) τ=500 s

(b) τ=1 000 s

Fig.15Transient temperature distribution of the drum section at different times

4　结　论

(1)导热反问题解法思路简单明了，求解结果更加精确，但仅适用于外壁不受热区域；导热正问题解法适用范围广，但计算精度不高.

(2)导热正反问题耦合解法弥补了单一方法求解存在的局限和不足，提高了计算结果的精度，实用性广泛，可适用于复杂边界条件下温度场的求解分析，具有一定的理论意义和较高的工程应用价值.

(3)采用Ansys软件对导热正反问题耦合解法进行验证，对比分析了不同位置处节点温度随时间的变化，结果表明导热正反问题耦合解法具有较高的精度，在复杂边界条件下具有很好的适应性，能够满足工程应用的需要.

[1]李立人, 陈玮, 盛建国, 等. 锅炉受压元件的高温蠕变-疲劳寿命设计计算方法[J].动力工程，2009,29 (5)：409-416.

LI Liren，CHEN Wei，SHENG Jianguo，etal. Creep-fatigue life design and calculation method for boiler pressure elements under elevated temperature[J]. Journal of Power Engineering, 2009, 29(5)：409-416.

[2]管德清，莫江春，张学纶，等.电站锅炉汽包寿命在线监测系统[J].动力工程，2002，22(6)：2044-2047.

GUAN Deqing，MO Jiangchun，ZHANG Xuelun，etal. Life on-line monitoring system for boiler drum of power station[J]. Power Engineering, 2002，22(6)：2044-2047.

[3]郑心伟，孙瑜，王晓军.增压锅炉汽包低周疲劳寿命计算方法研究[J].热能动力工程，2010，25(2)：184-189.

ZHENG Xinwei，SUN Yu，WANG Xiaojun. Study of the methods for calculating the low-cycle fatigue life of a supercharged boiler drum [J]. Journal of Engineering for Thermal Energy and Power, 2010，25(2)：184-189.

[4]刘彤，徐钢，庞力平，等.锅炉炉内承压部件的蠕变分析及寿命计算[J].动力工程，2004，24(5)：631-635.

LIU Tong，XU Gang，PANG Liping，etal. Creep analysis and life calculation of the pressure components inside boiler[J]. Power Engineering, 2004，24(5)：631-635.

[5]HU Wensen，LI Bin，CAO Zidong，etal. An inverse method for online stress monitoring and fatigue life analysis of boiler drums[J]. Journal of Chongqing University (English Edition)，2009，8(2)：89-96.

[6]贾鸿祥，林友新．调峰机组锅炉汽包温度场解析[J]．西安交通大学学报，1994，28(6)：92-98．

JIA Hongxiang，LIN Youxin．The analysis of temperature field in the steam generator drum wall for cyclic loading units[J]．Journal of Xi'an Jiaotong University，1994，28(6)：92-98．

[7]赵铁成，沈月芬，朱国桢．电站锅炉锅筒温度场计算——三维非稳态变物性材料不均匀导热问题有限元分析[J]．中国电机工程学报，1997，17(4)：217-220.

ZHAO Tiecheng，SHEN Yuefen，ZHU Guozhen. Temperature field calculation of boiler drum—finite element analysis of 3-D unsteady variable character uneven material heat conduction problem[J]. Proceedings of the CSEE，1997，17(4)：217-220.

[9]CEBULA A，TALER J. Determination of transient temperature and heat flux on the surface of a reactor control rod based on temperature measurements at the interior points[J]. Applied Thermal Engineering，2014，63(1)：158-169.

[10]JAREMKIEWICZ M，TALER D，SOBOTA T. Measuring transient temperature of the medium in power engineering machines and installations[J]. Applied Thermal Engineering，2009，29(16)：3374-3379.

[11]MURIO D A．The mollification method and the numerical solution of the inverse heat conduction problem by finite differences[J].Computers & Mathematics with Applications,1989,17(10):1385-1396.

[12]TALER J，ZIMA W．Solution of inverse heat conduction problems using control volume approach[J]．International Journal of Heat and Mass Transfer，1999，42(6)：1123-1140．

[14]田广，赵海飞．增压锅炉锅筒内压应力三维有限元分析[J]．锅炉制造，2013 (1)：61-64．

TIAN Guang，ZHAO Haifei．Mechanical stress analysis of supercharged boiler drum by 3-D finite element method[J]．Boiler Manufacturing，2013 (1)：61-64．

A Coupling Method of Direct and Inverse Heat Conduction Problems for Transient Temperature Calculation of a Boiler Drum

LIBin，CHENFeng，SHILiangxiao

(School of Energy, Power and Mechanical Engineering, North China Electric Power University,Baoding 071003, Hebei Province, China)

A coupling method of direct and inverse heat conduction problems was proposed for transient temperature calculation of a pressurized boiler drum, of which the locally heated outer surface is divided into two regions, namely heated and unheated area. For the unheated area, the inverse method is used to determine the temperature field by circumferentially arranging thermocouples to measure the outside surface temperature of the drum, and for the heated area, the direct method is adopted to solve the temperature field; whereas at the junction of above two areas, the temperatures determined by the inverse method are used as known boundary conditions to calculate the temperature field of heated area by the direct method. By this way the coupling solution of direct and inverse heat conduction problems is realized, and the whole temperature distribution of the drum is obtained. A comparison was made to the drum temperature distribution during cold startup of the boiler respectively obtained by Ansys software and the coupling method. Results show that the coupling method of direct and inversion heat conduction problems has high precision and strong adaptability under complicated boundary conditions, which therefore may be used in actual engineering projects.

boiler drum; temperature field; inverse heat conduction problem; direct heat conduction problem; coupling method of direct and inverse heat conduction problem

A学科分类号：470.30

2014-02-17

2014-06-05

李斌(1969-)，男，河北保定人，副教授，博士，主要从事传热过程数值模拟和热力系统性能分析等方面的研究.

陈丰(通信作者)，男，硕士研究生，电话(Tel．)：15132461127；E-mail：chenfeng1513246@163.com．

1674-7607(2015)02-0096-07

TK223