min型与max型线性规划问题解法探析
2015-08-16赵云平
赵云平
(临沧师范高等专科学校数理系,临沧 云南677099)
min型与max型线性规划问题解法探析
赵云平
(临沧师范高等专科学校数理系,临沧 云南677099)
min型(max型)线性规划问题就是如何在有限的资源条件下,追求最小化(最大化)的问题。大量教材中多以max型为例向学者展示了线性规划问题的求解。如何求解min型线性规划问题?文章在给出max型解法的基础上,给出了min型问题的解法,帮助学者更好的区分和认识不同类型线性规划问题的求解。
min型;max型;线性规划问题;单纯形法;检验数
线性规划是运筹学最重要的分支,也是最成熟的一个分支,自从1947年美国人丹捷格提出求解线性规划的比较规范的单纯形法以来,它在理论上已趋向成熟,实际的应用日益广泛与深入。min型和max型是线性规划模型的两种形式,而单纯形法又是求解线性规划问题的主要的、有效的算法。单纯形法是一种迭代的算法,迭代就是用一种模式反复进行。单纯形法的思想是在基本可行解中寻优。单纯形法的主体步骤有三步[1-7]:首先确定初始基本可行解;检验其是否最优,若是,计算停止;若不是,寻找更好的基本可行解。恒量两个解的优劣用目标衡量,谁使目标最优谁更好,2、3两步为循环往复的过程,直到找到最优。下面针对min型与max型线性规划问题的求解,通过举例给以详细说明[5-7]。
1 min型线性规划问题的求解
将模型化为标准形式是用单纯形法求解线性规划问题的初始步骤。标准形式的线性规划模型中,目标函数为求极小值(或极大值),约束条件全为等式,约束条件右端常数项全为非负值,变量的取值均非负。
例1用单纯形法求解下列线性规划问题[5]
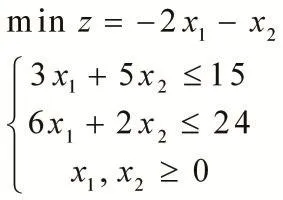
分析:首先第一步将模型化为标准形式,通过添加松弛变量把约束变为等式,观察系数阵中是否含单位阵I,如果化为标准型后系数阵中仍然不含I,那就需要用人工变量法,人为的添加出一个I来,总之初始的系数阵中应该有一个,因为单纯形法的第一个基取为I。化为标准型后,而且含I,就可以上单纯形表进行计算了。

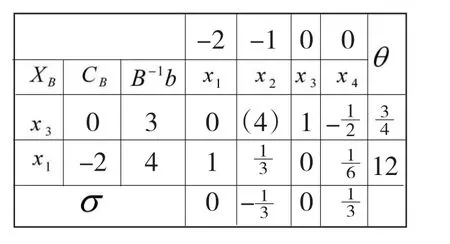
初始单纯形表:

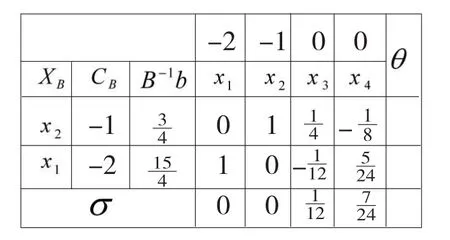

2 max型线性规划问题的求解
下面我们仍以例1为例,通过添加负号的形式将min型转化为max型进行求解[6,7],即,因为一个函数求极小点的问题可以化为求极大点的问题,这二者是同解的,它们的值互为相反数。选用同一题目目的为了更清楚的看到两种类型的不同与相同之处。

初始单纯形表:
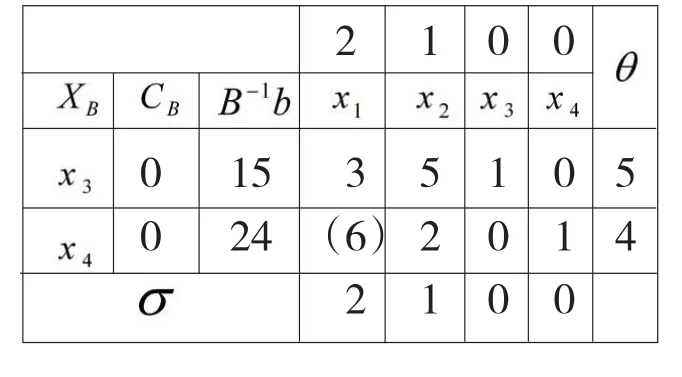
用公式计算检验数,
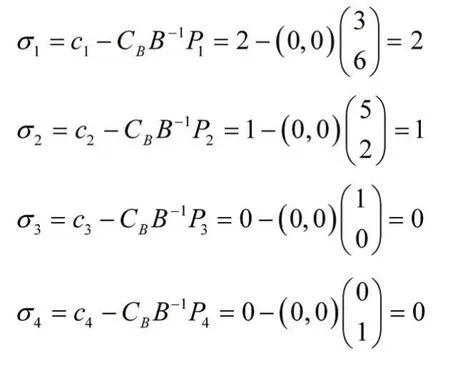

检验数数中仍有大于0的,故当前解X=(4,0,3,0)T不是最优。正检验数所对应的变量就进基,同样的方法计算检验比,B-1b与进基列对应元素之比,即3比4等于,4比等于12,检验比中最小的所对应的就出基,以进基列与出基行的交叉元4为出发点遵循相同的原则进行迭代,得到下一张单纯形表。


3 小结
一个简单的例题,两种不同的解法,min型与max型在解法上几乎相同,区别仅在于检验数反号,即min型是令负检验数中最小者对应的变量进基,当检验数均大于等于零时当前解为最优;max型是令正检验数中最大者对应的变量进基,当检验数均小于等于零时当前解为最优。相仿,对于max型线性规划模型可以用max求解,也可转化为min型求解。线性规划问题中还有很多方面有待研究。
注释及参考文献:
[1]《运筹学》教材编写组.运筹学[M].4版.北京:清华大学出版社,2012.
[2]何坚勇.运筹学基础[M].北京:清华大学出版社,2008.
[3]邓成梁.运筹学的原理和方法[M].北京:华中科技大学出版社,2014.
[4]胡运权.运筹学基础及应用[M].4版.哈尔滨:哈尔滨工业大学出版社,2006.
[5]《运筹学》教材编写组.运筹学[M].3版.北京:清华大学出版社,2005:20-28.
[6]胡运权,郭耀煌.运筹学教程[M].4版.北京:清华大学出版社,2012:12-27.
[7]杨民助.运筹学[M].西安:西安交通大学出版社,2000:30-53.
[8]曾梅清,田大刚.线性规划问题的算法综述[J].科学技术与工程,2010(1):153-159.
[9]范国兵.线性规划问题最优解的讨论[J].怀化学院学报,2012(11):81-83.
[10]曾国斌.线性规划问题的相关算法研究[J].赤峰学院学报,2014(10):1-2.
AnAnalysis on the Solutions of MIN-MAX Type Linear Programming Problems
ZHAO Yun-ping
(Department of Mathematics and Science,Lincang Teachers’College,Lincang,Yunnan 677099)
Type Min(Max)linear programming problem is how to pursue the minimization(maximization)of problem under a condition with limited resources.Examples with type Max have been adopted to present the solutions of linear programming problems for scholars in majority of textbooks;but how about the solutions of type Min linear programming problems?Grounded on the type Max solutions,solutions of type Min problems will be figured out in the following essay,which aims at offering scholars a better distinction and clearer recognization of solutions for different linear programming problems.
type Min;type Max;linear programming problem;simplex method;check number
O221.4
A
1673-1891(2015)01-0019-03
2014-09-15
赵云平(1982-),女,云南临沧人,硕士,讲师,研究方向:基础数学数论应用,应用数学运筹学线性规划,数值代数。
