关于一阶非齐次线性微分方程的求解问题

吴小兰

（福建电力职业技术学院，福建 泉州362000）

关于一阶非齐次线性微分方程的求解问题

吴小兰

（福建电力职业技术学院，福建 泉州362000）

给出并证明了两个定理，利用这两个定理求解一阶非齐次线性微分方程。

非齐次；线性；微分方程；求解

引言

高等教育的大众化，使得大学生整体素质普遍下降，近年来每况愈下。对于高职院校来说，学生基础差尤为严重，由于高中数学知识掌握差缺和没有养成好的学习习惯和方法，高等数学成为大学生学习的拦路虎，如果处理不当，将影响后续课程及专业课的学习，打击学生的学习积极性和自信心。因此教师在高数教学过程中要注重对数学问题的归纳和总结，让复杂的问题简单化，易于理解，便于学生掌握和应用，帮助学生克服畏难情绪，培养学生的学习兴趣，激发学生的创新思维。

1 两个定理

从方程1的左边结构特点和乘积的求导法则，我们假设方程的左边乘以一个适当的函数后成为一乘积求导式子，即设想存在函数使得：

由此得到定理1.

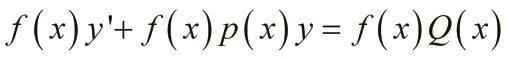
2 应用举例

解：利用定理1求解

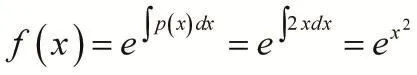
显然，该方法省去了常数变易法必须的乘积和复合求导后再代入方程化简的复杂过程，使问题的解决更加简单方便。

解法一：利用常数变易法求解

通过两种方法的对比，可以发现，利用常数变易法对非齐次线性方程的通解求导过程中，涉及到了三个函数相乘的导数和复合函数求导，是学生学习的难点，也是学生比较容易出错的。而利用定理求解，则避免了上述求导运算，简化了求解过程。

4 小结

两个定理的结论简单易记，对应的求解方法通俗易懂，省略了一些复杂的计算过程，直观明了。高职院校基础课程教育改革，各学科在教学中,应以增进学生创造才能为主要任务,以解决问题为主题、以学生自主活动为主要方式，加强探究性学习。教师在高等数学的教学中，应针对学生学习中存在的问题和遇到的困难，采取有效的方法，注重对数学问题的归纳和总结，让复杂的问题简单化，通俗易懂，便于学生掌握和应用，激发学生的学习兴趣和创新性。

注释及参考文献：

[1]何新萌，张奕河．高等数学下册[M]．福建:厦门大学出版社,2008:10．

[2]同济大学数学教研室．高等数学下册[M]．北京:高等教育出版社,2002:348．

[3]张奕河,吴小兰．不定型极限求法研究[J]．贵阳学院学报(自然科学版),2013（2）:13-15．

On Solving Problems of First Order Non Homogeneous Linear Differential Equation

WU Xiao-lan
(Fujian Electric Vocational and Technical College，Quanzhou，Fujian 362000)

This paper presents and proves two theorems,using the two theorems for the solutions of first order non homogeneous linear differential equation.

non homogeneous;linear；differential equation；solution

O175.1

A

1673-1891（2015）01-0017-02

2014-07-29

吴小兰（1981-），女，福建泉州人，硕士，讲师，研究方向：高职数学教学和研究。