全概率公式和贝叶斯公式教学新探*
2015-08-16任芳玲
任芳玲,刘 瑞
(延安大学 数学与计算机科学学院,陕西 延安716000)
全概率公式和贝叶斯公式教学新探*
任芳玲,刘 瑞
(延安大学 数学与计算机科学学院,陕西 延安716000)
全概率公式和贝叶斯公式是概率论教学的一个重难点,一般的授课方法是直接给出公式内容,对照例题套用公式,学生接受起来比较困难,理解不了公式的内涵。笔者结合课堂实践采取一种新的授课方式:结合实例给出应用背景、引导学生理解公式内涵、妙用概率树图法求解公式,以此方法简化了思考过程且达到了学以致用的目的,收到了很好的教学效果。
全概率公式;贝叶斯公式;教学研究;概率树图
引言
在日常生活中,我们周围的许多事物都和概率有着千丝万缕的联系,所以将概率知识和实际相结合是概率教学应该把握的一个基本方向。全概率公式和贝叶斯公式作为概率论课程中两个重要的基础内容,是解决概率问题的两个重要思想,恰如其分的应用这两个公式是概率学习的一个重点。笔者通过几年来对概率论课程的教学研究,反复总结自己多次教学过程的优缺点,结合学生在理解接受上存在的问题,发现讲透应用背景和简明清晰的求解方法是讲解全概率公式和贝叶斯公式的重要方面。引入概率树图法求解,并将好的实例作为数学实验课程的一个例子,以此可调动学生的学习热情并提高学生用概率知识解决实际问题的能力,实施于课堂教学发现是行之有效的。结合全概率公式和贝叶斯公式的应用背景,给出以下实例:
实例1:提出排球比赛赛制,热心的球迷总有提前估计中国队夺冠可能性大小的好奇心,引出用全概率公式可以满足球迷的这种好奇心.
实例2:重温《狼来了》的故事,调动学生对诚信教育经典之作的回忆,引出用贝叶斯公式可求解故事中撒谎小孩的可信度是如何降低的。
实例3:提出一个肇事逃逸案件,在一个初冬大雾天的下午六点左右发生了一起交通事故,肇事车是本市一辆出租车,该车早已逃逸。有一个目击者认定是一辆绿色出租车,若你是交警,你能确信目击者的证言吗?引出用贝叶斯公式可以判断目击者证言可信度的大小。
1 定理内容及内涵解析
1.1 全概率公式
定理1[1]:设是一个完备事件组,则对任一事件B,有
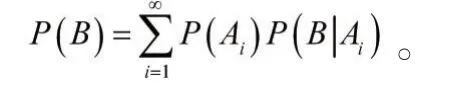
1.2 全概率公式解析
(1)在全概率公式中,事件B可理解为某一结果,事件Ai可理解为引起结果B的某个原因,P(Ai)表示某个原因发生的可能性大小,表示原因Ai引起结果B的可能性大小,而结果B是由各个原因综合作用的,所以可理解为公式的直观作用是“知因求果”[2]。
(2)全概率公式的“全”指的是对结果事件B有贡献的全部原因,并且这些原因构成一个完备事件组。
(3)公式中蕴含了一个加法公式和乘法公式,是一种加权求和的形式,如此将事件分解,便可使复杂的事件简单化。
1.3 贝叶斯公式
定理2[1]:设是一个完备事件组,则对任一事件B,有
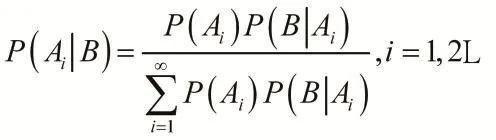
1.4 贝叶斯公式解析
(1)贝叶斯公式符合条件概率的形式。贝叶斯公式的分母是“全概率公式”要解决的问题,分子是分母和式中的一项。
(2)贝叶斯公式的直观作用可理解为是“执果探因”。即已知结果事件B已经发生了,探求导致这一结果发生的某个原因Ai的可能性大小,所求的是条件概率
(3)P(Ai)指的是试验以前人们根据以往的数据经验得出的概率,称为先验概率,指的是试验已经发生,对事件Ai概率的重新估计,称为后验概率。
2 公式的应用
2.1 直接应用公式
全概率公式的应用步骤:(1)判断是否符合全概率公式的应用背景;(2)找出样本空间的完备事件组;(3)求出每一原因事件的概率P(Ai);(4)求出原因对结果影响的概率P(Ai)。
贝叶斯公式的应用步骤:(1)判断是否符合贝叶斯公式的应用背景;(2)找出样本空间的完备事件组;(3)求出结果事件的概率P(B);(4)针对任一原因求出P(Ai)P(Ai)。
例1:试卷中有一个四选项的单选题,任一考生如果会做这道题,则因为粗心做错的概率是0.05;如果他不会做这道题,则任选一个答案,设考生会解这答题的概率是0.8,求:(1)考生做对的概率?(2)如果考生答对了,则他确实会做这道题的概率是多少?
分析:将考生“做对”看作是结果事件B,将考生“会做”和“不会做”看作是导致结果发生的两个原因事件A和,且A和构成一个完备事件组,可见问题1符合全概率公式的应用背景,问题2符合贝叶斯公式的应用背景。则
2.2 利用概率树图求解
树图就是按事件发生的先后顺序作出图,它的形状像一棵树,有根、分支、节点和末梢,然后再按原途返回求解。在表示随机现象的树形图的各线段上,标上相应的率,这种树称为概率树[3]。树图法主要是利用乘法原理,在上面树形结构中,在一整个路径上,从根到末梢,事件发生的概率等于各段分支上概率的乘积。
例2:假定在某次世界女排赛中,中、日、美、古巴四队取得半决赛权,半决赛时的分组是中国对阵古巴,美国对阵日本,那么在比赛之前如何根据以往的比赛数据估计此次比赛中国队夺冠的概率呢?
(1)若中国队已经战胜古巴队出线,且根据以往的战绩,假定中国队战胜日本队、美国队的概率分别为0.9与0.5,而日本队战胜美国队的概率为0.5,试问中国队取得冠军的可能性有多大?
解:做出概率树图
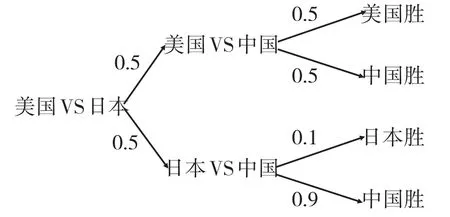
可见符合全概率公式的应用背景,设中国队取得冠军为事件B,则根据树图法的原理,中国队夺冠有两条路径,可得:
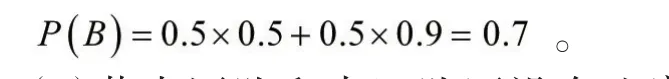
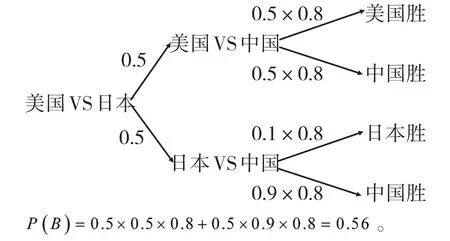
(2)若中国队和古巴队还没有比赛,且中国队战胜古巴队的概率是0.8,那么如何估算中国队取得冠军的可能性有多大?
做出概率树图
例3:用贝叶斯公式重温一下“狼来了”的故事[4],看小孩子第三次喊“狼来了!”的时候村民对他的信任度怎样变化?
解:设事件B表示小孩可信、事件A表示小孩说谎,先做一些假设:村民起初对这个小孩的可信度是0.8,即P(B)=0.8,我们认为可信的孩子说谎的可能性为0.1,即,不可信的孩子说谎的可能性为0.5,即
解:做出概率树图
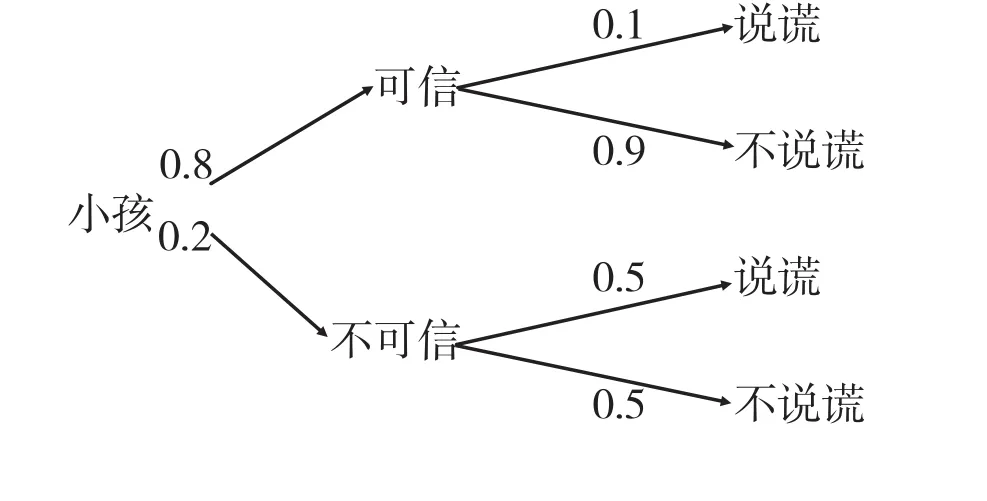
可见问题符合贝叶斯公式的应用背景,村民第一次上山,小孩说了谎,这时村民对小孩的可信度为:
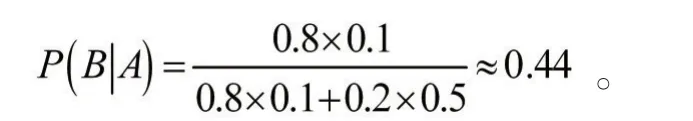
由此可见,小孩第一天说谎后,其可信度由0.8下降到0.44.同理做出概率树图可得
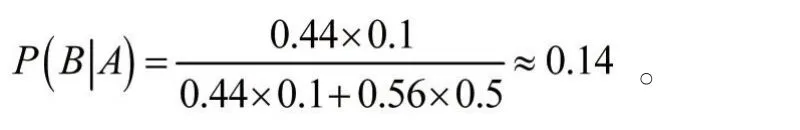
由此可见,小孩第二天说谎后,其可信度已经下降到0.44,如此低的可信度导致再也没有人来救他了。
例4:在一个初冬大雾天的下午六点左右发生了一起交通事故,肇事车是本市一辆出租车,该车早已逃逸.有一个目击者认定是一辆绿色出租车,若你是交警,你能确信目击者的证言吗?
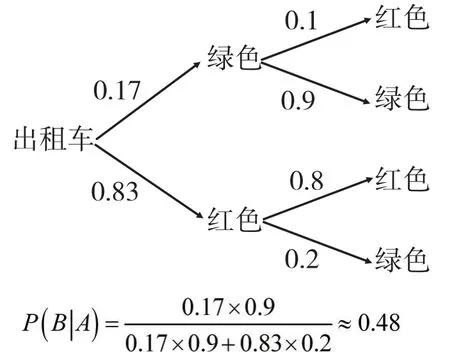
解:假定经调查该市有红、绿两种颜色的出租车,其中绿色占17%,红色占83%,我们假定通过测试可知,目击者将红色看成红色的概率为0.8,将红色看成绿色的概率为0.2,将绿色看成绿色的概率为0.9,将绿色的看成红色的概率为0.1.用贝叶斯公式可判断目击者证言可信度的大小。
设事件B表示肇事出租车确实是绿色的,事件A表示目击者看到的肇事车是绿色的,那么做出概率树图
根据计算,在这种情形下目击者尽管说的是真话,但他判断正确的概率也只有0.48,所以交警要想破案,还得收集更有力的证据。
由此可见树图法思路清晰,极为便捷,不易出错,但必需注意两个条件:
(1)每一分支后的事件必须是互不相容的,即它们的概率和必需为1;
(2)从第一个节点之后,路径中的概率均为条件概率。
特别是当层次分的越多越复杂时,树图法更能显示出它的优越之处,对于理解公式,提高解题能力可起到事半功倍的作用。
3 结语
“知因求果”和“执果探因”是全概率公式和贝叶斯公式理解的精髓,概率树图是求解全概率公式和贝叶斯公式很好的方法,将实例始终穿插于教学过程的始终是调动学生学习积极性的有力手段。这样的教学方法既能让学生很好的理解枯燥难懂的定理公式,也能让学生感觉到概率的美和无处不在。
注释及参考文献:
[1]刘新平.概率论与数理统计[M].西安:陕西师范大学出版社,2010.
[2]符方健.全概率公式及其应用技巧[J].高等数学研究,2011,14(2):52-54.
[3]李晓红.概率树在全概率公式中的应用[J].高等数学研究,2008,11(2):60-62.
[4]张丽,闫善文,刘亚东.全概率公式与贝叶斯公式的应用及推广[J].牡丹江师范学院学报(自然科学版),2005(1):15-17.
New Teaching Exploration of the Total Probability Formula and the Bayes Formula
REN Fang-ling,LIU Rui
(College of Mathematics and Computer Science,Yan’an University,Yan’an,Shaanxi 716000)
The total probability formula and the bayes formula are the key and difficult points in probability teaching.The general teaching method is that the contents of the formulas are given directly,then used mechanically, It is difficult for students to accept and understand the connotation of the formulas.A new teaching method is adopted by the author combining classroom practice,giving the application background in combination with examples,leading the students to understand the connotation of the formulas,using the probability tree graph method wonderfully to solve the formula,so that the method can simplify the thinking process and make us study for the purpose of application.and has achieved a very good teaching result.
the total probability formula;the bayes formula,teaching research;probability tree graph
O211.1
A
1673-1891(2015)01-0014-03
2014-10-15
延安大学教学改革研究项目:“三驱”教学法在大学数学教学中的应用研究(项目编号:YDJG14-10)。
任芳玲(1984-),女,陕西富县人,讲师,硕士,主要从事概率统计和金融数学研究。
