Al代位合金化对D88-Ti5Si3力学性能与电子结构影响的第一性原理研究

黄豪杰　徐　江（南京航空航天大学材料科学与技术学院，南京210016）

Al代位合金化对D88-Ti5Si3力学性能与电子结构影响的第一性原理研究

黄豪杰徐江*
（南京航空航天大学材料科学与技术学院，南京210016）

采用基于密度泛函理论（DFT）的第一性原理赝势平面波方法，计算了不同数量的Al原子代位六方D88结构的Ti5Si3晶体中的Si原子后的形成能（ΔHf）、结合能（ΔEcoh）、体模量（B）、剪切模量（G）、泊松比（ν）、Cauchy压力参数（C12―C66，C13―C44）、金属性（fm）和派-纳力（τP-N）等参数，表征了Al合金化对D88-Ti5Si3的结构稳定性和力学性质的影响.结合态密度、差分电荷密度图和Mulliken布居等电子结构分析，揭示了Al原子的添加量对D88-Ti5Si3的韧/脆性变化的影响机制.研究表明，D88-Ti5Si3晶体中强的Ti6g―Si6g方向共价键是导致其室温脆性的主要原因.当1个和2个Al原子占据D88-Ti5Si3晶体中Si6g位置时，形成了键强较弱的Al6g―Si6g键、Ti6g―Al6g键和Ti4d―Al6g键，同时降低了D88-Ti5Si3中Ti6g―Si6g键的强度和数量，从而提高了D88-Ti5Si3的韧性.当D88-Ti5Si3晶体中Si6g位置被3个Al原子所占时，Al6g―Si6g键消失，而Ti6g―Si6g键的强度增加，导致Ti5（Si1-xAlx）3的脆性增加.

第一性原理；钛硅化合物；化学键；韧/脆性；电子结构

www.whxb.pku.edu.cn

1　引言

随着现代工业的的迅猛发展，相关领域对高温结构材料的性能提出了更高的要求.当前广泛使用的镍基高温合金服役温度已超过其熔点绝对温度的80%，难以满足新一代高推重比、高增压比和高涡轮前温度发动机对热端部件材料的性能需求.研制开发具有能耐更高温度、比强度更高的新型高温结构材料替代镍基高温合金已势在必行.

继Mo-Si系金属硅化物，Ti-Si系金属硅化物在高温结构材料、耐磨材料、高温抗氧化涂层等方面展现出巨大的应用前景，被认为是极具竞争力的新一代高温结构候选材料.在Ti-Si系金属硅化物中，Ti5Si3以其高熔点（2130°C）、低密度（4.32 g·cm-3）、高硬度（11.3GPa）以及优异的高温力学性能和抗高温氧化能力等诱人的物理化学性能，备受国外材料工作者的普遍关注.1，2然而Ti5Si3复杂六方D88晶体结构对称性差，独立的滑移系数目不足，导致其具有强的室温本征脆性.3此外，Ti5Si3晶体中a轴方向原子间是以共价键形式结合，而c轴方向原子间是以较弱的金属键形式结合，导致其呈现出强烈的热膨胀系数各向异性，使得多晶Ti5Si3在高温制备随后的冷却阶段产生较大的内应力，加剧该材料的脆性失效.4Ti5Si3具有金属键和共价键共存的原子键合特性，其优于陶瓷材料之处在于可通过添加合金化元素以置换或间隙原子的形式存在于Ti5Si3晶体中，提高晶体的对称性、改变电子结构、结合键的类型与强度以及降低热膨胀系数的各向异性，从而改善其室温脆性.Mitra等5利用三点弯曲法评价了添加8%（w）Al的Ti5Si3的断裂韧性，结果表明，Al合金化可一定程度上改善Ti5Si3的断裂韧性.Schneibel等6研究了添加不同过渡金属元素对Ti5Si3的热膨胀各向异性的影响.结果表明：所添加过渡金属无论是占据较大的Ti6g位置或者占据较小的Ti4d位置，均能降低c轴上的热膨胀系数.Zhang和Wu7的研究表明，添加Nb比Cr在降低Ti5Si3热膨胀系数各向异性方面效果更显著.Ikarashi等8的研究表明，添加间隙原子B、C、N、O等均能降低Ti5Si3的热膨胀各向异性，其中添加一定量的C效果最为显著.

在传统的实验研究中，科研工作者常采用“试错法”筛选出理想的材料，不仅缺乏明确的设计准则，而且需要耗费大量的人力、物力和财力，以及较长的研究周期.随着计算机技术的不断进步以及量子力学方法的不断发展，第一性原理计算方法在材料研究方面发挥越来越重要的作用.第一性原理计算不借助任何经验参数，仅依靠量子力学的基本常数，将电子作为研究对象，可以从原子尺度深入理解材料的成分、结构和性能三者之间关系，为实验合金成分设计提供了强有力的理论工具，从而显著提高研究效率.近年来，基于密度泛函理论的第一性原理计算方法，已在Ni-Al系、9，10Ti-Al系11及Mo-Si系12-15等金属间化合物的机械性能的研究方面取得了一系列成果.本文基于第一性原理的密度泛函理论，计算了不同化学计量比Ti30Si18-xAlx的平衡结构性质、弹性参数、力学性质和电子特性，从电子结构层次上分析了造成Ti5Si3脆性的主要原因，揭示了不同Al原子数置换Si6g原子对Ti5Si3韧/脆性的影响规律，为探索合金化改善Ti5Si3的室温脆性方面提供了理论基础.

2　计算模型与参数

2.1计算模型

Ti5Si3属Mn5Si3型复杂六方D88结构，如图1所示，其空间群为P63/mcm，晶格参数为a=b=0.7461 nm，c=0.5151 nm，a=β=90°，γ=120°.Ti5Si3晶体中有3种等效位置点，其格点坐标分别为Ti6g（0.247，0，0.250），Ti4d（0.333，0.667，0）和Si6g（0.606，0，0.250）.在D88结构Ti5Si3晶体中，Ti4d原子排列在平行于c轴的线型原子链上（A原子面），Ti6g原子和Si6g原子则位于密排原子面B和C上，在密排原子面B和C上原子的排列相同，但B和C原子密排面之间旋转了180°，16三种基本原子面按ABACA的顺序堆垛.计算利用D88原胞构建了由48个原子组成的1×1×3超晶胞，分别使用1个、2个和3个Al原子取代Ti30Si18中的Si6g原子，研究Al合金化对Ti5Si3性能的影响.

2.2计算参数

所有计算工作均通过基于密度泛函理论的第一性原理超软赝势平面波方法的CASTEP （Cambridge Serial Total Energy Package）程序软件包实现.17在计算晶格常数、合金形成能和结合能、弹性常数时，利用周期性边界条件，晶体波函数由平面波基组展开，电子交换关联能函数采用广义梯度近似（GGA）中的Perdew-Burke-Emzerhof关系式进行处理.18，19为了满足计算的精度并提高计算速度，所有的计算均在倒易空间中进行.利用Monkhorst Pack方法确定布里渊区的k点值为4×4×2，经过收敛性测试后平面波截断能设置为450 eV.在计算之前先采用Brodyden-Fletcher-Goldfarb-Shanno（BFGS）最小化方法20对所建模型进行几何优化，以获得局域最稳定结构，具体的收敛参数如下：体系总能量收敛精度为5.0×10-5eV·atom-1，原子平均受力小于0.1 eV·nm-1，最大应力收敛值为0.02 GPa，最大距离收敛值为5.0×10-4nm.

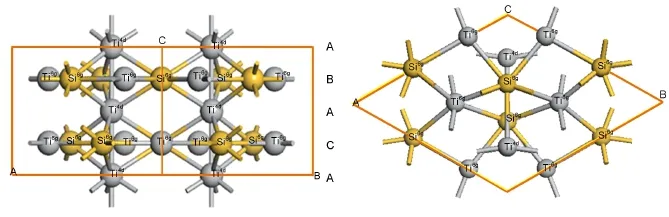
图1　Ti5Si3的晶体结构Fig.1　Crystal structure of Ti5Si3Front view and side view.A，B，and C mean different atomic planes in Ti5Si3.

3　计算结果与讨论

3.1结构稳定性

表1列出了驰豫优化后基态下的Ti30Si18-xAlx的晶格常数以及计算所得到的形成能和结合能随Al原子的添加量的变化.对于D88-Ti5Si3而言，计算得到的晶格常数与文献6所报道的实验值非常接近（误差小于0.3%），而形成能与Williams等21采用LMTO方法计算获得的结果相差不到3%，表明本工作所采用的计算方法和计算中所选取的参数设置是可靠的.从表1可见，D88-Ti5Si3的晶格常数a、c以及c/a随着Al含量的增加而逐渐增大，这是由于代位Al原子的半径（0.182 nm）大于Si原子的半径（0.146 nm）所引起的.形成能（ΔHf）反映了不同类型原子从其单质状态生成化合物所释放或吸收的能量，形成能为负值时，表示形成该化合物的过程是放热过程，形成能愈小，晶体的热力学稳定性越高.材料热力学稳定性也可以用结合能（ΔEcoh）来评价.结合能的绝对值越大，晶体中内部原子之间结合力愈强，代表该化合物的结构越稳定.表1中四种Ti30Si18-xAlx的形成能和结合能均为负值，表明它们在热力学上具有稳定结构.两者的绝对值随Al含量的增加而逐渐减小，反映其结构稳定性逐渐降低.

表1　计算得到的Ti30Si18-xAlx的晶格常数、形成能（ΔHf）和结合能（ΔEcoh）Table 1　Calculated values of Ti30Si18-xAlx，including lattice parameters，formation enthalpies（ΔHf），and cohesive energies（ΔEcoh）

表2　计算得到的Ti30Si18-xAlx的弹性常数（Cij）（单位：GPa）Table 2　Calculated elastic constants（Cij）for Ti30Si18-xAlx（unit：GPa）

3.2材料的弹性性质和韧/脆性

六方D88-Ti5Si3晶体有六个不同的二级弹性常数，由表2可知，所计算的Ti30Si18-xAlx弹性常数皆满足Born-Huang稳定性判据，22表明四种Ti30Si18-xAlx合金符合力学稳定性要求.本文计算的弹性常数与Kishida等23利用RPR方法测定的单晶Ti5Si3的室温弹性常数基本吻合，表明本文的计算方法是合理的.弹性常数C11和C33分别反映了晶体在a和c方向上抵抗正应变的能力.随着Al含量的增加，弹性常数C11逐渐减小而C33呈现先减小后增加的趋势.由弹性常数C44和C66值变化可知，随着Al添加量的增加，Ti30Si18-xAlx合金抵抗剪切应变的能力呈现先减小后增大的趋势.通过上述计算的弹性常数，按照Voigt-Reuss-Hill（VRH）24公式可计算得到四种Ti30Si18-xAlx合金的体模量（B）、剪切模量（G）、杨氏模量（E）和泊松比（ν），计算结果如图2所示.由图可见，随着Si6g位置被更多的Al原子占据时，Ti30Si18-xAlx的体模量值逐渐减小，而杨氏模量值和剪切模量值表现出先减小后增加的趋势.材料硬度的大小主要取决于位错移动的能力，而剪切模量（G）比体模量更能反映材料抵抗位错移动的能力.25，26通常材料的剪切模量（G）越大，硬度也越大.Jhi等27认为，材料的硬度与弹性常数C44存在单调对应关系，即C44越大，材料硬度越高.因此，根据G和C44可以推测出随着Al原子的添加量增加，Ti30Si18-xAlx合金的硬度将呈现先减小后增大的趋势.

泊松比（ν）值不仅反映了材料横向变形的难易程度，而且反映了材料弹性力学状态下原子键长和键角的相对变化关系.通常泊松比越大，则材料的塑性越好.28泊松比值为0.25到0.5之间，原子间的相互作用主要表现为中心力形式.由图2可知，Ti30Si18-xAlx合金的塑性随Al添加量的增加，呈现先增大后减小的趋势.Pugh29指出材料的体模量B与剪切模量G的比值可判断材料的脆/韧性（也称为Pugh经验判据），B/G值越大，材料的韧性愈好.当B/G＜1.75时，材料呈脆性，反之，材料呈韧性.由B/G值的变化可以判断，随着Al含量的增加，B/G值逐渐增加，当2个Al原子取代Si原子时，B/G值接近于脆/韧临界值，而当三个Si原子被Al原子所取代时，B/G值为1.395，略低于两元D88-Ti5Si3的B/G值，表明该Al添加量导致其脆性增加.

图2　Ti30Si18-xAlx的体模量（B）、剪切模量（G）、杨氏模量（E）、泊松比（v）和B/G计算值Fig.2　Calculated bulk moduli（B），shear moduli（G），Yong′smoduli（E），Poisson′sratio（v）and B/G ratio for Ti30Si18-xAlx

Cauchy压力值判据表征了材料内部原子间成键的角度性质，30反映了材料的塑性.对于以金属键结合的材料，柯西压力为正，且数值越大金属键越强，材料的延展性越好，而对于以共价键结合的材

料，Cauchy压力值为负，且负值越小，材料的共价键越强，材料的脆性越大.对于六方晶系，柯西压力值由弹性常数差值C12-C66、C13-C44决定.16，23从图3可见，Ti30Si18-xAlx合金的C12-C66和C13-C44分别为正值和负值，表明这四种合金具有金属键和共价键共存的特征，两种Cauchy压力值随Al含量的变化规律与泊松比和B/G值的变化完全一致.

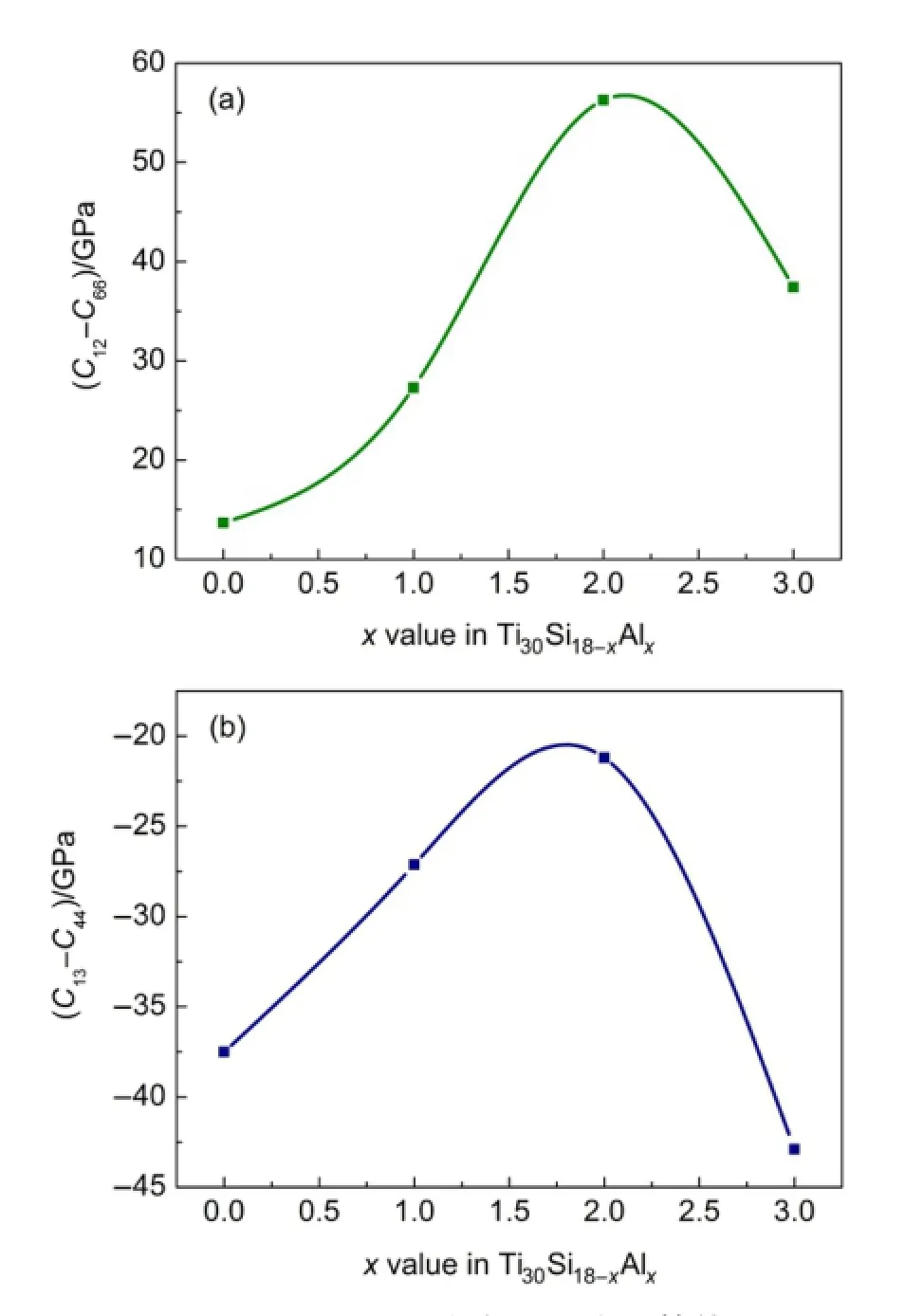
图3　Ti30Si18-xAlx的柯西压力计算值Fig.3　Calculated Cauchy pressures for Ti30Si18-xAlx（a）C12-C66；（b）C13-C44

金属的塑性变形主要是通过位错运动得以实现，而塑性变形过程中，开动位错需要克服来源于滑移面上、下两层原子间的引力所引起的晶格阻力或晶体点阵的位垒，即派-纳力（τP-N）.派-纳力越大，位错滑移受到的阻力越大，材料的塑性变形能力越小.派-纳力由下面的公式计算：31其中，w=a/（1-ν），G为材料的剪切模量，ν为材料泊松比，b为原子间距，a为晶面间距.

Kishida等23研究了D88-Ti5Si3单晶体在1200-1500°C的压缩变形行为，利用透射电镜观察了D88-Ti5Si3单晶体中所存在的七种位错滑移系，并计算了这七种位错滑移的派-纳力.结果表明：｛1100｝［0001］滑移系具有最小的派-纳力，也是最易开动的位错滑移系.因此，本文计算Al合金化对｛1100｝［0001］滑移系位错运动的阻力τP-N的影响，结果见图4.从中图4可以看出，随着Ti30Si18-xAlx中Al原子数的增加，在开动滑移系｛1100｝［0001］所需的派-纳力先减小后增大，即位错的可动性随Al添加量的增加，呈现先增加后减小的趋势.上述四种韧/脆判据（泊松比、Cauchy压力、B/G比以及派-纳力值）皆表明，随Al原子取代Si原子数量的增加，Ti30Si18-xAlx的韧性呈现先增加后减小的变化.

3.3电子结构

材料的机械性能在一定程度上与其化学键的性质紧密相关，添加代位合金化元素往往会引起材料的电子态密度及电荷分布等内在电子结构特性的变化，从而影响其宏观机械性能.为了进一步深入理解Al原子取代Si6g原子对D88-Ti5Si3韧脆性的影响，本文对Ti30Si18-xAlx的态密度、差分电荷密度和Mulliken布居等电子结构进行了分析，初步揭示了Al含量变化对D88-Ti5Si3韧/脆性变化的原因.

3.3.1态密度

图5（a）为Ti5Si3的总态密度（TDOS）和分波态密度（PDOS）图.本文计算所得到的Ti5Si3态密度图与Chen、32Ekman33和Williams21等得到的态密度图完全吻合.由图可见，在费米能级以下-10.5--6.0 eV能量区域处，主要由Si的3s轨道占据，该区间仅在-8.3 和-7.2 eV位置处出现Si的3s轨道与Ti的3d轨道发生微弱的交叠；在-5.0--1.5 eV能量区间，主要由Ti的3d与Si的3p轨道占据，在-4.2、-2.3和-1.5 eV处分别对应三个成键峰，两者之间产生较明显的共振，说明Ti与Si原子之间形成了p-d杂化；在-1.5 eV到费米能级处，主要由Ti-3d轨道占据，Ekman等33指出，Ti6g之间不能直接成键，因而该区间内最可能包括Ti4d的3d轨道之间交互作用的电子以及形成Ti的非键态电子.

当采用1个和2个Al原子取代Si6g位置后，Ti30Si18-xAlx的TDOS曲线在-6.0--5.2 eV的能量区间内出现了一个小的成键峰，该区间主要由Al的3s轨道和Si 3p轨道占据，表明该区间形成了较弱的Al―Si共价键；在-5.0--1.5 eV能量区间，波形变得更平缓，表明该区间内电子的局域性减弱.从Ti30Si18-xAlx的PDOS曲线可见（图5（b）和图5（c）），在-5.0--2.0 eV能量区间内，Si的3p轨道的态密度曲线成键峰明显减弱，Ti的3d轨道的态密度值减小，说明Si的3p轨道与Ti的3d轨道杂化减弱. 在-1.5 eV到费米能级处，Al的3p轨道的态密度曲线与Ti的3d轨道的态密度曲线有明显的共振现象，这显示Al的3p轨道与Ti的3d轨道存在强烈的交互作用.在费米能级附近，Ti4d的3d轨道态密度值减小，Ti4d之间的交互作用减弱.图5（d）显示，当3个Al原子取代Si6g位置后，在-6.0--5.2 eV能量区间内Al―Si共振峰消失，而在-5.0--1.5 eV成键区，Si 的3p轨道的态密度值明显增加，表明Ti与Si原子之间的p-d杂化再次增强.此外，从总态密度图可见，四种Ti30Si18-xAlx合金的费米能级附近均出现了深谷，即存在赝能隙.赝能隙是成键态与非键态的分界，当费米能级位于赝能隙的右侧时，所有的成键态全部被电子占据，多余的电子填充到反键态，此时电子越少，成键态在体系中所占的比重越大，化合物的结构会越稳定；当费米能级位于赝能隙的左侧时，则成键态未完全被电子填满，化合物未达到稳定结构.34，35由图5可见，赝能隙均位于费米能级附近，这四种合金的较高的结构稳定性，而高的结构稳定性取决于所存在强的方向共价键，导致Ti5Si3合金具有高的室温脆性.36对于二元Ti5Si3，其费米能级恰好在能隙处，表明二元Ti5Si3的d（Ti4d）-d（Ti4d）能态完全被占满.随着Al原子的添加量增加，Ti30Si18-xAlx的费米能级由能隙的谷底向高能处移动，这与反键的生成有关.根据费米能级为非零值可知，四种Ti30Si18-xAlx合金的都具有一定的金属特性.按照Li 等37提出化合物金属性（fm）的计算方法可知（结果见表3），四种Ti30Si18-xAlx合金的金属性随着Al原子的添加量增加，呈现先增强后减弱的趋势.

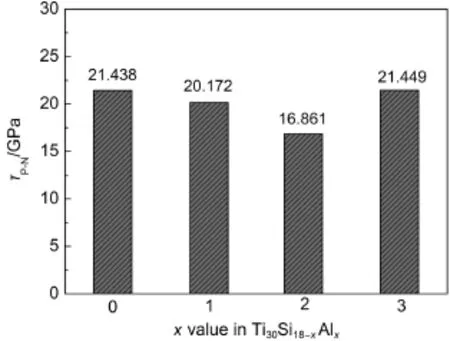
图4　Ti30Si18-xAlx｛1100｝［0001］滑移系的派-纳力计算值Fig.4　Calculated Peierls stress of slip system ｛1100｝［0001］for Ti30Si18-xAlx

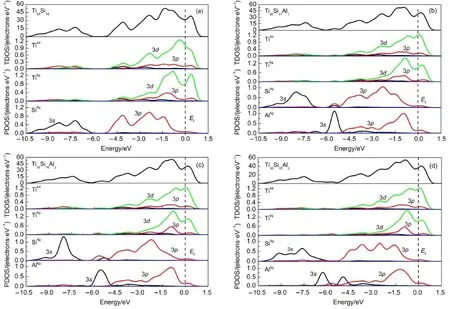
图5　四种Ti30Si18-xAlx合金的总态密度（TDOS）和分波态密度（PDOS）曲线Fig.5　Total density of state（TDOS）and partial density of state（PDOS）curves of four kinds of Ti30Si18-xAlxalloys

3.3.2差分电荷密度

差分电荷密度图可以直观地显示原子之间的电子转移及成键的极性强弱.图6和图7分别给出了四种Ti30Si18-xAlx合金（110）和（110）面的差分电荷密度图.由图6（a）可见，Ti6g原子的电荷密度分布呈花瓣状，表明Ti6g原子的电荷密度分布具有各向异性，而Si6g的电荷密度分布呈三角形结构，相邻的两个Ti6g与Si6g的电子云之间相互有联通，说明Ti和Si原子周围出现强的电荷转移.两者间所形成的这种强的具有方向性的共价键会导致不同滑移系派-纳力差异很大，易形成派纳力深谷，造成位错塞积，使得位错运动受阻.38当一个或两个Si6g原子被Al原子取代后，Ti6g与Si6g之间的重叠电子云明显减弱，其中部分Ti6g的电子云与Al的电子云相互连接，表明Ti6g―Si6g共价键的强度降低，同时形成了Ti6g―Al键，有利于提高塑性.当采用3个Al原子取代Si6g原子时，Ti6g与Al6g之间的电子云重叠减少，Ti6g与Si6g的电子云重叠再次增加，Ti6g―Si6g共价键变强，导致脆性增加.另外，从图7（a）中可见，Ti4d原子之间形成了具有一定方向性的化学键，表明该金属键含有一定的共价键成分.在两个Ti4d链之间，有形成Ti6g―Si6g键的电子投射到（110）面而形成的沿Ti4d链方向的柱状电子云，随着置换原子Al的增加，该柱状电子云的面积呈现出先减小后增大的变化趋势，也再次证实了Ti6g―Si6g键强度由弱变强的变化过程.

表3　计算的Ti30Si18-xAlx的费米能级处态密度值（DOSf），价电子总数（N），晶胞体积（Vcell）和金属性参数（fm）Table 3　Calculated density of states at the Fermi surface （DOSf），total numbers of valence electrons（N），the cell volume（Vcell）and metallicity parameter（fm）of Ti30Si18-xAlx

3.3.3Mulliken布居

Mulliken电荷布居表征了电荷在各组成原子之间的分布情况，可定量分析不同原子轨道在化学成键中的作用.正的和负的布居值分别表示成键和反键态，而接近零的布居值则指两个原子间的电子布居没有显著作用，说明该键是离子化的.16

图6　四种Ti30Si18-xAlx合金（110）面的差分电荷密度图Fig.6　Charge density difference on（110）plane of four kinds of Ti30Si18-xAlxalloys

图7　四种Ti30Si18-xAlx合金（110）面的差分电荷密度图Fig.7　Charge density difference on（110）plane of four kinds of Ti30Si18-xAlxalloys

表4　四种Ti30Si18-xAlx合金的Mulliken布居、键长和键数*Table 4　Mulliken populations，bond lengths and numbers of bond for four kinds of Ti30Si18-xAlxalloys*

由表4中可知，四种Ti30Si18-xAlx合金中，d（Ti4d）―d（Ti4d）的布居值均为负值，表明d（Ti4d）―d（Ti4d）成键轨道全部占满，有微弱的d（Ti4d）―d（Ti4d）反键形成，随着Al原子的添加量增加，Ti4d－Ti4d反键的键强先减小后增大.由文献16可知，Ti6g中的价电子主要有两个方面的贡献：一个是Ti6g与Si6g成键，另一个就是非键.在四种Ti30Si18-xAlx合金中，二元Ti5Si3的Ti6g―Si6g键的布居值最大，键长最短，且键的数量也最多，该键也是导致Ti5Si3的室温脆性主要原因.当采用1个和2个Al原子取代Si6g位置后，Ti6g―Si6g的键长增加，布居值减小，且同时出现了键强较弱的Ti4d―Al6g、Al6g―Si6g和Ti6g―Al6g键，表明增加Al原子的数量有利于降低Ti6g―Si6g的键强以及非键的增强，从而一定程度上改善了Ti5Si3的韧性.当3个Al原子取代Si6g位置后，Ti6g―Si6g键的布居值增大而键长减小，键强较弱的Al6g―Si6g键消失，这表明Ti30Si18-xAlx中非键在减弱，金属性下降，从而导致其脆性增加.

4　结论

基于第一性原理的计算方法，采用1-3个Al原子置换Si6g原子，研究了Al代位合金化对D88-Ti5Si3的结构稳定性与力学性能的影响，并从电子结构角度揭示了添加不同Al含量对D8-TiSi的韧/脆性变化的相关机制，主要结论如下：

（1）根据剪切模量和C44可以推测出随着Al添加量的增加，Ti30Si18-xAlx合金的硬度将呈现先减小后增大的趋势.

（2）D88-Ti5Si3中强的Ti6g―Si6g共价键是其产生室温脆性的主要原因.当采用1个和2个Al原子取代Si6g位置后，Ti6g―Si6g共价键的强度和数量减少，B/G值和泊松比（v）增大，｛1100｝［0001］滑移系的派-纳力降低，从而提高这两种Ti30Si18-xAlx合金的韧性.

（3）当三个Si原子被Al原子所取代时，B/G值和泊松比减小，｛1100｝［0001］滑移系的派-纳力增加，Ti6g―Si6g键的布居值增大而键长减小，键强较弱Al6g―Si6g键消失，导致其脆性增加.

References

（2）Mitra，R.；Prasad，N.E.；Mahajan，Y.R.Trans.Indian Inst.Met. 2008，61，427.doi：10.1007/s12666-008-0075-5

（3）Dimiduk，D.M.；Miracle，D.B.；Ward，C.H.Mater.Sci. Technol.1992，8，367.doi：10.1179/mst.1992.8.4.367

（4）Williams，J.J.；Kramer，M.J.；Akinc，M.J.Mater.Res.2000，15，1780.doi：10.1557/JMR.2000.0257

（6）Schneibel，J.H.；Rawn，C.J.Acta Mater.2004，52，3843.doi：10.1016/j.actamat.2004.04.033

（7）Zhang，L.T.；Wu，J.S.Scripta Materialia 1998，38，307.

（8）Ikarashi，Y.；Ishizaki，K.；Nagai，T.；Hashizuka，Y.；Kondo，Y. Intermetallics 1996，4，141.doi：10.1016/0966-9795（96）80193-2

（9）Jiang，C.；Sordelet，D.J.；Gleeson，B.A.Scripta Mater.2006，54，405.doi：10.1016/j.scriptamat.2005.10.023

（10）Djajaputra，D.；Cooper，B.R.Phys.Rev.B 2002，66，205108. doi：10.1103/PhysRevB.66.205108

（12）Qiao，Y，J.；Zhang，H.X.；Hong，C.Q.；Zhang，X.H.J.Phys.D：Appl.Phys.2009，42，105413.doi：10.1088/0022-3727/42/10/ 105413

（13）Waghmare，U.V.；Kaxiras，E.；Bulatov，V.V.；Duesbery，M.S. Modell.Simul.Mater.Sci.Eng.1998，6，493.doi：10.1088/0965-0393/6/4/013

（14）Fu，C.L.；Wang，X.D.Philos.Mag.Lett.2000，80，683.doi：10.1080/09500830050143787

（15）Fu，C.L.；Wang，X.D.；Ye，Y.Y.；Ho，K.M.Intermetallics 1999，7，179.doi：10.1016/S0966-9795（98）00018-1

（16）Wang，H.Y.；Si，W.P.；Li，S.L.；Zhang，N.；Jiang，Q.C. J.Mater.Res.2010，25，2317.doi：10.1557/jmr.2010.0293

（17）Segall，M.D.；Lindan，P.J.；Probert，M.A.；Pickard，C.J.； Hasnip，P.J.；Clark，S.J.；Payne，M.C.J.Phys.：Condens. Matter 2002，14，2717.doi：10.1088/0953-8984/14/11/301

（18）Perdew，J.P.；Chevary，J.A.；Vosko，S.H.；Jackson，K.A.；Pederson，M.R.；Singh，D.J.；Fiolhais，C.Phys.Rev.B 1992，46，6671.doi：10.1103/PhysRevB.46.6671

（20）Fischer，T.H.；Almlof，J.J.Phys.Chem.1992，96，9768.doi：10.1021/j100203a036

（21）Williams，J.J.；Ye，Y.Y.；Kramer，M.J.；Ho，K.M.；Hong，L.；Fu，C.L.；Malik，S.K.Intermetallics 2000，8，937.doi：10.1016/ S0966-9795（00）00064-9

（22）Born，M.；Huang，K.；Lax，M.Am.J.Phys.1955，23，474.

（23）Kishida，K.；Fujiwara，M.；Adachi，H.；Tanaka，K.；Inui，H.Acta Mater.2010，58，846.doi：10.1016/j.actamat.2009.09.062

（24）Yang，F.；Fan，T.W.；Wu，J.；Tang，B.Y.；Peng，L.M.；Ding，W. J.Phys.Status Solidi B 2011，248，2809.doi：10.1002/ pssb.201147247

（25）Brazhkin，V.V.；Lyapin，A.G.；Hemley，R.J.Philos.Mag.A 2002，82，231.doi：10.1080/01418610208239596

（27）Jhi，S.H.；Ihm，J.；Louie，S.G.；Cohen，M.L.Nature 1999，399，132.doi：10.1038/20148

（28）Xu，J.；Wu，J.D.；Lai，D.H.；Xie，Z.H.；Munroe，P.Mater.Sci. Technol.2012，28，1337.doi：10.1179/1743284712Y. 0000000069

（31）Lu，G.The Peierls-Nabarro Model of Dislocations：AVenerable Theory and Its Current Development.In Handbook of Materials Modelinged；Springer：Amsterdam，2005；pp 793-811.

（32）Chen，X.J.；Zeng，M.X.；Wang，R.N.；Mo，Z.S.；Tang，B.Y.；Peng，L.M.；Ding，W.J.Comput.Mater.Sci.2012，54，287. doi：10.1016/j.commatsci.2011.10.042

（34）Ravindran，P.；Nordstrom，L.；Ahuja，R.；Wills，J.M.；Johansson，B.；Eriksson，O.Phys.Rev.B 1997，57，2091.

（35）Ravindran，P.；Subramoniam，G.；Asokamani，R.Phys.Rev.B 1995，53，1129.

（36）Wang，Y.J.；Wang，C.Y.Appl.Phys.Lett.2009，94，261909. doi：10.1063/1.3170752

（37）Li，Y.F.；Gao，Y.M.；Xiao，B.；Min，T.；Fan，Z.J.；Ma，S.Q.；Xu，L.L.J.Alloy.Compd.2010，502，28.doi：10.1016/j. jallcom.2010.04.184

（38）Greenberg，B.A.；Antonova，O.V.；Indenbaum，V.N.；Karkina，L.E.；Notkin，A.B.；Ponomarev，M.V.；Smirnov，L.V.Acta Metall.Mater.1991，39，233.doi：10.1016/0956-7151（91）90271-2

First-Principles Study into the Effect of Substitutional Al Alloying on the Mechanical Properties and Electronic Structure of D88-Ti5Si3

HUANG Hao-JieXU Jiang*
（School of Materials Science and Technology，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，P.R.China）

The influence of the substitution ofAl for Si on the structural stability and mechanical properties of D88-Ti5Si3was determined using first-principles pseudopotential plane-wave methods based on density functional theory.Several parameters including formation enthalpies（（ΔHf），cohesive energies（ΔEcoh），bulk modulus（B），shear modulus（G），Poisson′sratio（ν），Cauchy′spressure（C12-C66，C13-C44），metallicity（fm），and Peierls stress （τP-N）were calculated.To develop a better understanding of the effects of substitutional Al alloying on the toughness/brittleness of D88-Ti5Si3from an electronic structure point of view the density of states，charge density differences and Mulliken population were determined.The results show that the intrinsic brittleness of D88-Ti5Si3comes from strong covalent bonding between Ti6gand Si6g.When one or two Ti atoms occupy Si sites in the D88-Ti5Si3crystal the intensity of covalent bonding between Ti6gand Si6gis reduced and the metallicity increases.This is accompanied by the presence of low intensityAl6g―Si6g，Ti6g―Al6g，and Ti4d―Al6gbonds.However，when three Ti atoms occupy Si sites in the D88-Ti5Si3crystal the Al6g―Si6gbonds disappear and the intensity of covalent bonding between Ti6gand Si6gincreases leading to an increase in brittleness.

First-principles；Titanium-silicon compound；Chemical bond；Ductile/brittle behavior；Electronic structure

October 30，2014；Revised：December 24，2014；Published on Web：December 24，2014.

O641

10.3866/PKU.WHXB201412242

The project was supported by the National Natural Science Foundation of China（51374130）andAeronautical Science Foundation of China （2013ZE52058）.

国家自然科学基金（51374130）和航空科学基金（2013ZE52058）资助项目

©Editorial office ofActa Physico-Chimica Sinica