早期混凝土湿度场精确模拟的实现

王　宁

（天津市市政工程设计研究院 ，天津300051）

早期混凝土湿度场精确模拟的实现

王宁

（天津市市政工程设计研究院 ，天津300051）

摘要：为了更加精确的模拟混凝土结构早期的湿度场，基于ABAQUS二次开发平台，开发了精确模拟早期混凝土温湿度场的子程序UMATHT和FELM，并通过对脚本语言Python的二次开发，实现了对温度场结果的自动读取与保存。最后，在湿度场模拟过程中，利用数据接口自动读取相应单元的温度场结果，考虑了温度对湿度场的影响，得到了对湿度场较精确的模拟。

关键词：早期混凝土；湿度场；二次开发；耦合分析

相关工程实例表明，早期混凝土结构产生的表面较浅裂缝，其主要诱因为结构自身水分消耗或丢失而引起的干缩变形。在不利条件下，这些裂缝很可能会进一步发展，进而影响结构的安全及耐久性。

随着研究的深入，学者们发现湿度扩散系数受自身湿度、温度、水灰比等的影响，并表现出一定的非线性关系［1-4］。但当温度变化剧烈时，则需要考虑温度对系数的影响并应当首先求解出温度场分布状态。Kim Jin-Keun［5］研究表明，湿度分布主要受湿度扩散作用影响，给出了湿度扩散系数是自身相对湿度函数的表达式。Roger P W和Niall H［1］计算过程中选用与温度相关的非线性湿度扩散系数，计算结果和试验结果吻合很好。

针对表面湿度交换系数，Bazant和Akita都各自有过详细的研究，但是目前还没有一个考虑所有影响因素的公式，目前普遍采用文献［6］中提出的改进公式。

同时，现阶段研究早期混凝土应力方面 ，一是没有考虑湿度变化的影响，另一方面是在分析湿度场过程中采用了单一的常数参数，这两方面都导致了对研究不精确性。因此，本文基于ABAQUS二次开发平台，开发了可以考虑温度及其他因素影响的湿度场模拟方法，为进一步精确研究结构应力、变形打下了基础。

1　基本理论

1.1成熟度

成熟度的核心思想是同种混凝土的不同部位不论它们的温度和时间怎么组合只要两者具有相同的成熟度值，则它们的强度是完全相同的。

Freiesleben Hansen等提出了一个基于混凝土温度历程来计算其成熟度的方程，该方程基于Arrhe-nius方程，并得到了多数学者的认可和应用。根据Arrhenius方程的混凝土成熟度（等效龄期）计算式为：式中：Ea为活化能（J・mol-1）；R为理想气体常数（8. 314J・mol-1・K-1）；Tr为参考温度（通常取293K），T为节点实际温度。对于混凝土来说：当绝对温度T≥293K时，Ea=33.5 kJ・mol-1；当T＜293 K时，Ea= 33.5+1.47×（293-T）（kJ・mol-1）。本文在计算时选用 Ea/R为恒定值2 700 K。

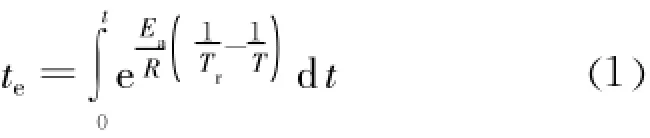
1.2温度场计算理论

水泥水化热是影响混凝土温度场的重要因素，但是传统方法在模拟过程中仅考虑了龄期对水化热的影响而忽略了温度的影响［7］，这与结构内部水化快、升温高、放热快的事实是不相符的［8］。因此，本文在模拟分析中采用基于水化度影响的温度场计算模型，同时采用变化的热学参数 ，旨在更加真实的模拟温度场结果。

一种合理的混凝土水化度可以定义为某时刻水化反应已释放的热量与最终完全释放的热量的比值，其表达式为［9］：式中：α（t）为 t时刻的水化反应程度；Q（t）为已放出的热量（J）；Qmax最终放热量（J）。

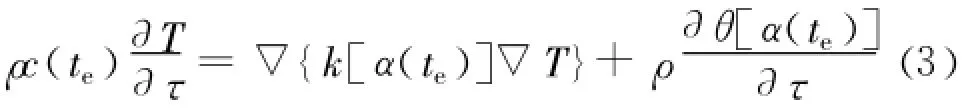
早期混凝土水化反应与自身的温度、龄期有关，其热学参数也随水化反应程度而不断变化。考虑以上因素后，其基于水化度建立的热传导方程为：式中：ρ为密度（kg・m-3）；c（te）为比热（kJ・kg-1・℃-1）；T为温度（℃）；k为基于水化度的导热系数（kJ・m-1・h-1・℃-1）；τ为龄期（h）；α（te）为基于等效时间的水化度；te为等效龄期。

在实际模拟过程中，因有限元不能直接计算积分公式 ，因此采用的是逐步叠加的方式来计算混凝土的等效龄期。具体计算公式如下：

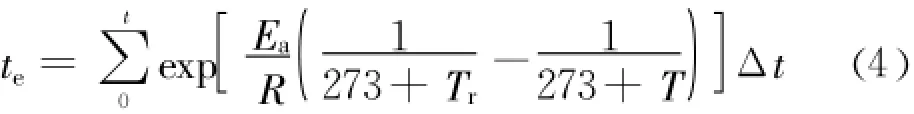
（1）导热系数 k

国外研究学者通过试验研究表明，早期混凝土的导热系数要比硬化后的值要大21% ～30%，且内部热传导系数要大于表面部位［10］，早期混凝土的导热系数可以通过与水化度相关的公式表达［11］。Schindler A K通过研究，给出了导热系数与水化度间的相互关系公式：式中：k（α）为热传导系数；ku为混凝土最终导热系数；α为水化度。

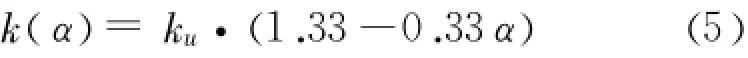
（2）比热c

国内外研究表明，早期混凝土比热受温度和自身水分含量影响较大。同时，在早期硬化之前，混凝土的比热与其水化度之间成线性反比关系。Van Breugel［12］通过对大量实验研究，给出了早期混凝土比热的公式：

式中：c为比热（kJ・kg-1・℃-1）；Wc，Wa，Ww分别为每立方水泥、骨料和水的质量（kg）；cc，ca，cw分别为水泥、骨料和水的比热值（kJ・kg-1・℃-1）；ρ为混凝土密度值（kg・m-3）；ccef为混凝土水泥的假定比热值（kJ・kg-1・℃-1）；α为混凝土水化反应水化度；Tc为当前温度（℃）。

1.3湿度场计算理论

混凝土材料是一种多孔复合材料，湿度扩散满足Fick第二定律，即认为物体内部可蒸发水流量 qx与物体内部湿度梯度成正比。同时，利用质量守恒定律，可以得到混凝土非稳定湿度场的扩散控制方程为：

式中：D（h）为混凝土湿度扩散系数；h为结构的相对湿度。

湿度场在模拟分析过程中，需要确定的参数有湿度扩散系数 D、表面湿度转移系数 f、大气环境相对湿度变化 he。

（1）湿度扩散系数 D

湿度扩散系数是描述结构湿度扩散能力的一个最重要的参数，受环境温度、湿度等因素影响较大。同时，由于早期混凝土温度场变化比较剧烈 ，必须考虑温度对湿度扩散系数的影响。综上，在温度场和湿度场共同作用下的湿度扩散系数表示为［13］：

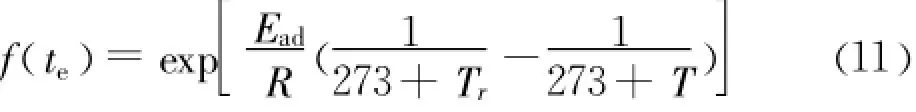
（2）表面湿度转移系数

表面湿度转移系数也称为表面水分交换系数，影响该参数的因素主要是水灰比、湿度梯度、温度和风速。表面湿度扩散系数可以采用更加符合实际的改进Menzel表达式［11］：

f（h-he）=A（0.253+0.06Va）（h-he）（12）式中：A为经验系数，取决于混凝土水灰比；Va为平均风速（m/s）；h、he分别为当时结构表面和大气的相对湿度值。

式中 ，D1.0取3.6×10-6m2/h；fck0取10.0 MPa；混凝土的抗压强度 fck可以由平均抗压强度fcm来估算，可取 fck=fcm-8.0 MPa。

2　关键技术说明

2.1两场耦合具体实施方案

本文采用顺序耦合方法实现了温度场、湿度场耦合分析，其耦合过程为将温度场的结果以荷载的形式施加于结构湿度场，考虑到温度对湿度场的湿度扩散系数的影响。顺序耦合的基本流程见图1。

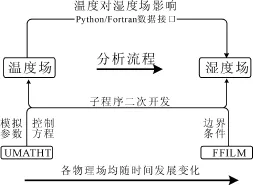
图1　顺序耦合过程示意图

2.2程序开发说明

对于早期混凝土温湿度场的模拟是利用子程序中的UMATHT和FILM两个子程序。子程序UMATHT可以用来模拟早期混凝土的水化放热过程；子程序FILM可以用来模拟混凝土与空气接触的边界条件。

与其他星座一样，人马座这片黑暗天区中同样散布着点点繁星，只是它们普遍没有那么亮，显得灰蒙蒙的。在那里，一颗名为S2（有时也称S-02）的小恒星正在永恒的边缘巡航。每16年，S2就会穿越一个神秘黑暗天体的势力范围，后者大概有400万个太阳那么重，正正好好占据着银河系的中心位置。

2.2.1子程序开发

子程序UAMTHT编写过程中，定义单位质量的内能U和热流失量FLUX是其至关重要的部分，也是子程序的核心部分。该子程序通过参数的编号能够模拟变化的比热、热传导系数。子程序FILM的关键部分是定义混凝土表面与大气之间的热交换系数，同时还有空气温度SINK。

2.2.2数据接口

因ABAQUS软件的前后处理和内核计算分别采用Python和Fortran语言编写，因此需要开发两个数据接口。一个是读取温度场计算结果的Python接口，一个是将温度场结果读入到子程序中参与计算的Fortran数据接口程序。

3　子程序合理性验证

选取某混凝土墙体进行合理性验证。模拟跨度为浇筑完成后（一次浇筑完成）的1200 h。图2给出了监测点的分布情况。混凝土及基岩材料参数见表1。

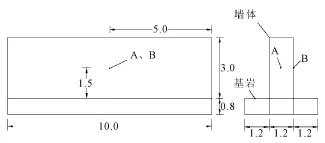
图2　混凝土墙体尺寸及监测点示意图（单位：m）

表1　混凝土材料参数

模拟过程中，基础底部和四周竖向面采用绝热边界，即假定相邻之间没有热量传递；基岩上表面及墙体四周面与大气接触部位选取合适的第三类边界条件。拟合后的空气温度变化公式为：

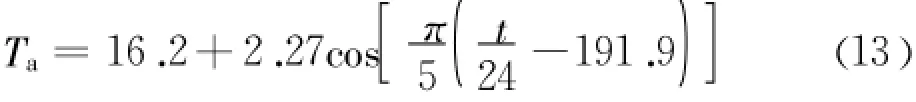
式中：t为距浇筑完成的时间（h）。

为了验证ABAQUS温度场子程序对于温度场分布模拟的合理性，考虑到大型通用软件ANSYS自带有可以模拟温度场的功能，因此采用两个软件计算结果对比的方法来验证合理性。简便起见，热交换系数取定值为45 kJ・m-2・h-1・℃-1。

图3和图4分别给出了监测点A、B温度变化历时曲线。

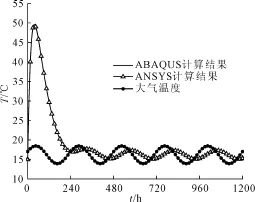
图3　监测点A 温度变化过程

图4　监测点B温度变化过程

计算结果表明，两种方法的计算结果完全一致。因此，本文对子程序UMATHT和FILM的开发是正确的。

4　湿度场精确模拟的实现

4.1有限元计算条件

湿度场模拟分析中，取100 mm×100 mm×500 mm的长方体进行模拟，同时利用结构形式的对称性，湿度场模拟过程中选取四分之一结构建模。有限元网格及监测点布置图见图5。参考相关文献［8］，湿度场计算参数取值见表2。

图5　监测点布置图

表2　湿度场计算参数

温度场和湿度场边界条件为四周面施加第三类边界条件，对称面施加绝热（湿）边界条件。计算时间为浇筑后的360 h。

考虑到早期混凝土温度变化较大，湿度扩散系数采用式（9）进行计算。其中，当前湿度值可以通过子程序中关键字TEMP直接获得，而要考虑温度场对参数的影响，就必须首先模拟相应的温度场分布，然后利用开发的Python程序，将温度场结果读取并存储，然后利用开发的Fortran子程序实现对相应温度值的读取，考虑温度对湿度场的影响。

湿度场计算过程中，为了输出要求需要设置一些状态，其具体含义见表3。

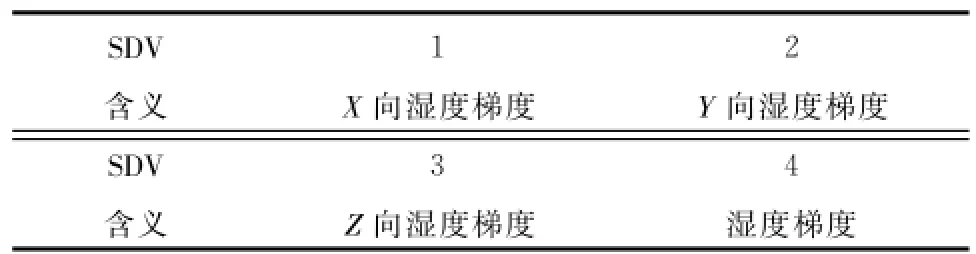
表3湿度场状态变量含义

4.2湿度场模拟结果

图6给出了混凝土浇筑后不同时刻结构的相对湿度场分布情况。图7给出各监测点湿度变化过程。

图6　不同时刻湿度场分布情况

从图6中可以看出，湿度场的变化程度非常缓慢，尤其是内部结构。这一点通过湿度场和温度场相应参数的量级对比就可以看出。内部点在浇筑后360 h相对湿度降低到0.9326，而此时表面点相对湿度为0.6004，已经十分接近大气环境的相对湿度。

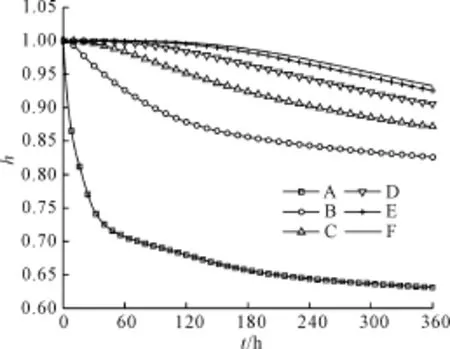
图7　监测点相对湿度变化过程

从图7中可以看出，在整个模拟过程中，表面点A的相对湿度变化最大，且在开始时刻就有较大的降幅，之后缓慢接近外部环境的相对湿度；其他监测点的变化幅度随着离表面的距离增大而减小，监测点E和F的相对湿度在前120 h内基本没有变化，之后才有小幅度的降低过程。从各个监测点相对湿度变化过程对比可以看出，相对湿度变化剧烈的部位主要位于结构表面约2.0 cm深度处，湿度梯度在表面部位较大。

图8给出了浇筑后不同时刻结构的湿度梯度分布云图。图9给出了各个监测点的湿度梯度变化过程曲线。

从图8中可以看出，结构表面的最大湿度梯度在360 h内经历了增大然后减小再缓慢增大的变化过程。因结构尺寸较小，内部的湿度梯度是一个增大过程，但数值较小，浇筑360 h后为0.485。结构湿度梯度最大主要出现在结构表面几毫米深度的部位，但是随着时间的推移，最大值区域在减小。

从图9中可以看出，在整个模拟过程中，表面点A的湿度梯度变化最为剧烈，经历了开始迅速增大，后减小，再缓慢增大的过程。监测点B、C、D都是经历了增大之后缓慢降低的过程，而点E和F还处于增大过程，但数值很小。由曲线可以看出，表面湿度梯度最大的部位约在边界内1.0 cm的范围内，因此干缩应力对结构表面浅裂缝的产生应该会有较大的影响。

图8　不同时刻湿度梯度分布情况

图9　监测点湿度梯度变化过程

5　结　论

（1）基于abaqus二次开发平台开发了精确模拟温度场的子程序UMATHT和FILM，并通过算例验证了子程序开发的合理性。利用脚本语言Python编写代码实现了对整个模拟时间内的温度场结果的自动读取与保存。

（2）工程算例表明，在模拟计算360 h后，结构仅仅在表面较浅部位有较大的湿度变化过程，而内部湿度变化非常小，湿度梯度表现为同样的规律。结构表面出现裂缝有干缩应力的显著影响，而内部应力状态受干缩现象影响不大。

参考文献：

［1］Roger P W，Niall H.Predicting moisture movement during the drying of concrete floors using finite elements［J］.Construction and Building Materials，2005，19（9）：674-681.

［2］黄达海，刘光廷.混凝土等温传湿过程试验研究［J］.水利学报，2002，（6）：96-100.

［3］黄达海 ，刘光廷.等温条件下混凝土质扩散系数研究［J］.应用基础与计算力学学报，2002，10（4）：386-394.

［4］张君，侯东伟.基于内部湿度试验的早龄期混凝土水分扩散系数求解［J］.清华大学学报：自然科学版，2008，48（12）：2033-2035.

［5］Kim Jin-Keun，Lee Chil-Sung.Moisture diffusion of concrete considering self-desiccation at early ages［J］.Cement and Concrete Research，1999，29：1921-1927.

［6］Yuan Y，Wan Z L.Prediction of cracking within early-age concrete due to thermal，drying and creep behavior［J］.Cement and Concrete Research，2002，32（2）：1053-1059.

［7］苏敏.工程混凝土早期温度应力分析及二次开发的研究［D］.哈尔滨：哈尔滨工业大学，2010.

［8］张岫文，叶列平，吴佩刚.基于成熟度的大体积混凝土早期温度应力场有限元分析［J］.建筑结构学报，2005，35（1）：68-71.

［9］Carino N J，Lew H S.The maturity method：from theory to application［J］.NIST，Gaithersburg（MD），2001.

［10］Jeong Jin-Hoon，Kim N.A thermal conductivity model for hydrating concrete pavements［J］.Journal of the Korea Concrete Institute，2004，16（1）：125-129.

［11］Schutter G De.Finite element simulation of thermal crackingin massive hardening concrete elements using degreeof hydration based material laws［J］.Computers and Structures，2002，80：2035-2042.

［12］Van Breugel K.Simulation of hydration and formation of structure in hardening cement based materials［J］.Cement &Concrete Research，1991.

［13］龚灵力.自密实混凝土性能及混凝土多场耦合时变性分析研究［D］.浙江：浙江大学，2010.

中图分类号：TU528

文献标识码：A

文章编号：1672—1144（2015）03—0110—06

DOI：10.3969/j.issn.1672-1144.2015.03.022

收稿日期 ：2015-01-30修稿日期 ：2015-03-12

作者简介 ：王宁（1987—），男，山东德州人，硕士 ，助理工程师 ，主要从事早期混凝土性态研究工作。E-mail：18698188237@126.com

Accurate Simulation of the Humidity Field of Early Age Concrete

WANG Ning
（Tianjin Municipal Engineering Design&Research Institute，Tianjin 300051，China）

Abstract：To obtain a more accurate simulation of humidity field of early-age concrete structure，based on the ABAQUS secondary development platform，subroutine UMATHT and FELM were developed to calculate the temperature and humidity field.And through the secondary development of the scripting language Python，the automatic reading and storing of temperature field result became possible.Finally，in the simulation of humidity field，the temperature field result of corresponding units was automatically read using subroutines with the consideration of the impact of temperature on the humidity field.Therefore the simulation of the humidity field using these subroutines is more accurate.

Keywords：early age concrete；humidity field；secondary development；coupling analysis