含风险调整适应函数的多资产价格动态模型
2015-08-11马鸿燕
马鸿燕
(伊犁师范学院数学与统计学院,新疆伊宁 835000)
含风险调整适应函数的多资产价格动态模型
马鸿燕
(伊犁师范学院数学与统计学院,新疆伊宁 835000)
本文主要研究在做市商机制下构建风险调整适应函数的多资产价格模型,考虑市场中具有两支风险资产和一支无风险资产,投资者为基本面分析者和图表分析者,其中图表分析者采用最简单的交易策略。并运用离散动力系统局部渐进稳定性和分支理论对其相应的确定性系统进行分析。
做市商; 风险调整; 图表分析者;稳定性
近年来,相关学者对异质信念资产定价进行了探讨与研究.异质信念资产定价和经典的定价模型的理性代表经济人相对应,假定市场参与者是有限理性的.Brock和 Hommes(1998)[1]提出异质信念贴现资产定价模型,将实现净利润作为适应函数,但是并未考虑到获得此利润时所承受的风险.在接下来的文献(如:Guanersdorfer,A.(2000)[2]、Hommes(2001)[3]、Gaunersdorfer,A.(2001)[4]、Gaunersdorfer and homes(2007)[5])中均引用适应函数为风险调整实现利润,因为由其推出的需求函数与均方差最大化推出的需求函数一致.Gaunersdorfer and homes(2007)[6]也引用了适应函数为风险调整型,其给出了证明波动聚集的理论.但对于风险调整适应函数都是在单资产模型中讨论.
市场出清价格的确定,有两种使用较广的瓦尔拉斯拍卖机制与做市商机制.其中前者被广泛引用于经济理论,并且O’Hara(1995)指出其仅用于伦敦的白银市场.有关于风险调整适应函数的模型都是在瓦尔拉斯拍卖机制下讨论的,本文主要探讨在做市商机制下含有风险调整适应函数的多资产价格动态模型.
1 模型
本文将建立含有风险调整适应函数的多资产价格动态模型.相关引用风险调整适应函数的文献(如:Guanersdorfer,A.(2000,2001)[2,4]、Gaunersdorfer and homes(2007,2008)[5-6])均考虑在瓦尔拉斯拍卖机制下讨论,本文考虑在做市商机制下讨论.

我们将在做市商机制下(参考Carl and he(2003)[13])调节市场价格,即
(1.1)
其中μ为每时期做市商调整市场价格的速度.
考虑两类具有简单信念类型的模型:
(a)基本面分析者
(1.2)
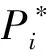
(b)图表分析者

(1.3)
其通过过去的历史价格导出其信念, (1.3)是一个他们通过最近观测到的价格变化作出交易规则的简单例子.如果g>0,则认为图表分析者为追风者;如果g<0,则认为其为逆风者.因此由(1.3)有
市场分数定义如下:首先,在演变部分,其由离散选择概率确定
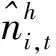
(1.4)
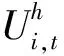
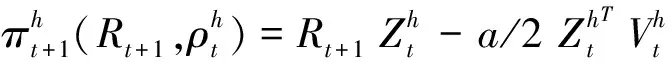
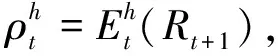
因此,风险调整实现净利润与财富短期期望最大化导出的需求函数一致的参考Gaunersdorfer and homes(2007)[5].定义适应函数为
经过推算得到

(1.5)
其中0≤η≤1是适应函数的记忆强度.
图表分析者考虑使用与基本价格的偏离程度决定他的市场分数,其模型为
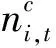
(1.6)
(1.7)
其中,




(1.8)
其中,





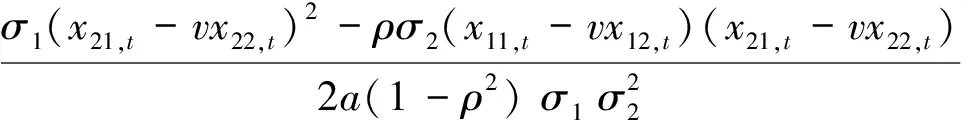

2 对模型相应的确定性系统进行稳定性讨论
在该部分,我们主要考虑对应的确定系统的不动点的存在性和在其附近的渐近稳定性.写出随机模型(1.8)对应的确定系统,即:
(2.1)

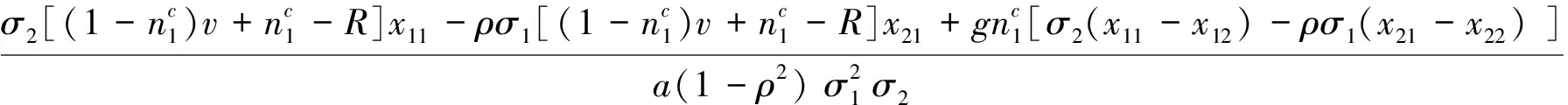

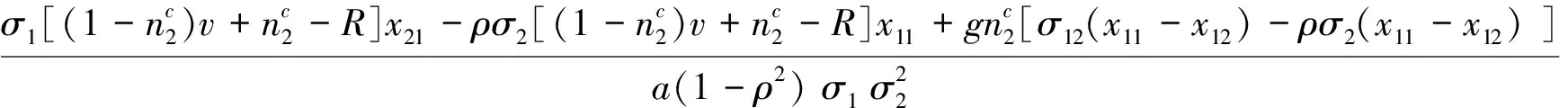

运用离散动力系统局部渐进稳定性和分支理论得到以下两个定理.


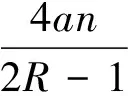
{0≤v≤vn,Ø}∪{vn {0≤v≤1,(2R-v-1)/2 {0≤v≤1,(1-v)/2 {0≤v≤1,(2R-v-1)/2-2am/μ 本文主要分析在做市商机制下构建含有两类投资者的风险调整型适应函数的多资产的定价模型.并且对相应的确定性系统的平衡点的存在性和唯一性进行讨论,使用差分动力系统稳定性相关理论讨论了多资产模型对应的确定性系统在不动点的稳定区域. 得到当μ增大时,系统在不动点的稳定区域逐渐缩小,说明当做市商调整市场价格的速度增大,做市商稳定市场的作用将会减弱,这一结论贴近于真实市场. [1]Brock,W.C. Hommes.Heterogeneous beliefs and routes to chaos in a simple asset pricing model[J].Journal of Economic Dynamics and Control,1998,22(8-9):1235-1274. [2]Gaunersdorfer,A.Endogenous fluctuations in a simple asset pricing model with heterogeneous beliefs[J]. Journal of Economic Dynamics and Control,2000,24(5):799-831. [3]Hommes, C.H. Financial markets as nonlinear adaptive evolutionary systems[J].Quantitative Finance,2001,1(1):149-167. [4]Gaunersdorfer,A.,Adaptive belief systems and the volatility of asset prices[J].Central European Journal of Operations Research,2001(9):5-30. [5]Gaunersdorfer A, Hommes C.A nonlinear structural model for volatility clustering[M].Berlin:Springer Berlin Heidelberg,2007. [6]Gaunersdorfer,A.,Hommes,C.H.Florian O.O Wagener. Bifurcation routes to volatility clustering under evolutionary learning[J].Journal of Economic Behavior and Organization,2008,67(1):27-47. [7]Chiarella, C.,He, X. Heterogeneous beliefs, risk and learning in a simple asset pricing model with a market maker[J].Macroeconomic Dynamics,2003,7(4):503-536. [8]Lux,t.,Herd behavior,bubbles and crashes[J].Economic Journal,1995,105(431):881-896. [9]王联,王慕秋.常差分方程[M].乌鲁木齐:新疆大学出版社,1991. EvolutionaryLearninginMulti-assetPricingModelwithaMarketMaker MA Hong-yan (Institute of Mathematics and Statistics, Yili Normal University, Yining Xinjiang 835000, China) In a market maker scenario, we develop a multi- asset pricing model with two types of rational traders,fundamentalists and chartists.Chartists use the simplest trading rule. Consider a two risky assets and a risk-free asset markets. Use local asymptotic stability of discrete dynamical systems and bifurcation theory for the analysis of underling deterministic system. market maker; evolutionary learning; chartists; stability 2015-05-13 马鸿燕(1990- ),女,宁夏海原人,伊利师范学院数学与统计学院助教,硕士,从事数理金融研究。 O211.9 A 2095-7602(2015)08-0014-05



3 结论
