基于曲率弦高法的海量测量数据精简

吴凤和， 王 鑫， 孙迎兵， 王 军

（燕山大学机械工程学院，河北秦皇岛066004）

基于曲率弦高法的海量测量数据精简

吴凤和， 王 鑫， 孙迎兵， 王 军

（燕山大学机械工程学院，河北秦皇岛066004）

针对视觉测量的点云数据过大而不利于计算和重构的问题，在分析视觉测量点云数据特征的基础上，将曲率原则和弦高法相结合，提出基于曲率弦高法的海量测量数据精简方法。该方法在考虑曲线曲率变化的基础上构建弦高函数，并通过迭代得到各测点变化的弦高值，再根据弦高法的数据精简原则确定需要保留的测量点。仿真实验表明，该方法在平均误差小于0.2 mm时，精简率为89.8%，能够有效地对海量点云数据进行精简，并实现精简后测点按曲面曲率的合理分布。

计量学；视觉测量；曲率；弦高；数据精简

1 引 言

在逆向工程中，根据测量方式的不同，数据采集方法可分为接触式测量和非接触式测量两大类［1］。其中，视觉测量以获取速度快、数据点呈一定规律性、精度较高等优点，被广泛应用于工业领域中［2～4］。但这种测量方法得到的数据量非常庞大，过多的数据点会减慢计算机的运算速度，占用大量内存，影响重构曲面的光顺性。实际上，不是所有数据对曲面重构都有用，而且数据存储或显示都将消耗大量的时间和计算机资源，所以在保证重构精度的前提下，对测量数据进行精简非常重要。

在视觉测量数据精简的研究中，国内外学者提出了各种不同的处理方法［5～10］，其中经常采用的方法是等弦长法和弦高法等。等弦长法程序简单、简化迅速，直接以测量点间的弦长作为简化依据，但当测量点分布不均匀时，该方法简化后的测量点在保持曲面几何特征方面效果较差。弦高法使用较为广泛，简化效果好，以连续点之间的弦高作为简化标准，基本能实现简化后测量点按曲面曲率合理分布。但该方法适合简化有规律分布的测量点，无法保留一些特殊的高曲率点。

本文在分析有关测量数据精简方面研究现状的基础上，提出一种基于曲率弦高法的海量测量数据精简方法。该方法以变化的弦高距离为基础，根据弦高法数据精简原理确定需要保留的测量点，并实现精简后测点按曲面曲率的合理分布。

2 改进的测量数据精简方法

2.1 弦高法原理

设定一个弦高值为Δh，令第一个点P1为基准点，比较连续点之间的弦高h1与Δh的大小，当h1＜Δh时，去除该点，然后连接后续点继续进行弦高比较，直到hi≥Δh；令Pi为新的基准点，重复上述步骤直到测量点均已处理完毕。该方法可在曲面曲率较小区域去除较多的测量点。其原理示意图如图1所示。

图1 弦高法原理示意图

这种方法采用了反映曲率变化的曲面特征参数作为数据精简的准则，且一般对已经结构化的点云适用性较好。但当相邻点相距很远时，即使曲率变化很小，弦高也可能很大；而相邻点相距较近时，即使弦高很小，曲率变化也可能很大，因此不能仅凭弦高或曲率变化对其进行约束。

2.2 曲率弦高法

根据视觉测量方法的点云数据分布特点，提出一种利用变弦高准则进行测量点精简的方法，即曲率弦高法，以相邻点之间的变化弦高作为测量点简化的判断标准。该方法将视觉测量的点云数据按截面线划分，沿着截面线方向，从截面线的一侧到另一侧，根据截面线的曲率变化计算出允许弦高值，即

式中：ρi为截面线上Pi点的曲率值；Δhj为截面线上保留的第j个点所对应的允许弦高值。

利用变化的允许弦高值来对截面线上的点进行逐条简化处理，其精简原理和程序流程分别如图2和图3所示。

图2 曲率弦高法原理示意图

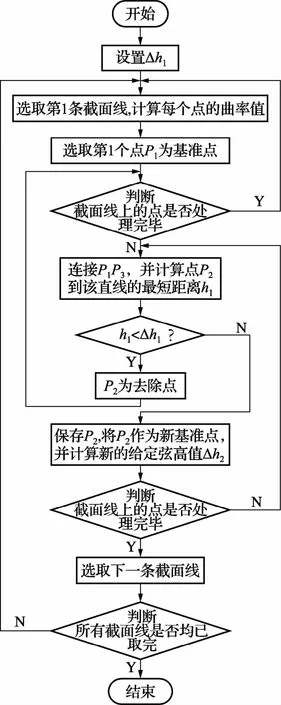
图3 曲率弦高法精简流程图

具体精简过程如下：

①首先确定一个允许弦高值Δh1；

②选取第一条截面线，并计算截面线上每个点的曲率值ρ1，ρ2，…，ρn，令截面线上的第1个点P1为基准点；

③连接基准点和它后面的第3个点P3，若P3不存在，则说明该段截面线上的所有点均已处理完毕，转到⑧；否则连成直线并计算第2个点P2的曲率ρ2和点 P2到该直线的最短距离 h1，hl＝sin（∠P2P1P3）；

④如果h1≥Δh1，则保留P2点，同时令P2点为新的基准点，转至③，同时令Δh2＝ρ1*Δh1／ρ2；

⑤如果hl＜Δh1，则去除P2点，同时连接基准点和在它后面的第4个点P4，若P4不存在，则说明截面线上的测量点都已处理完毕，然后转到⑧；否则，连成直线并计算点P2、P3到该直线的距离h2、 h3。h2＝sin（∠P2PlP4），h3＝sin（∠P3PlP4）；

⑥如果h2≥Δh1或h3≥Δh1，则保留P3点，同时令它为基准点，转至③；

⑦如果h2＜Δh1且h3＜Δh1，则去除P3点，转至⑤，依次类推；

⑧判断所有截面线是否都已取完，如果没有取完，则选取下一条截面线，转至②；否则，说明测量点云简化结束。

3 精简效果对比分析

为了验证曲率弦高法的简化效果，本文分别采用等弦长法、弦高法和曲率弦高法对测量点的点云数据进行处理，对3种方法点云简化后的效果图进行对比，并通过点云的精简率、重构曲线的平均误差和简化时间3方面指标来对简化方法进行评价。简化结果比较如图4所示。

选取不同的操作参数（Δd、Δh和Δh1），正弦曲线上的点云原始数据点为201个，采用等弦长法、弦高法和曲率弦高法进行精简，得到的简化数据如表1所示。其中包含点云的精简率、重构曲线的平均误差和简化时间等方面的指标。

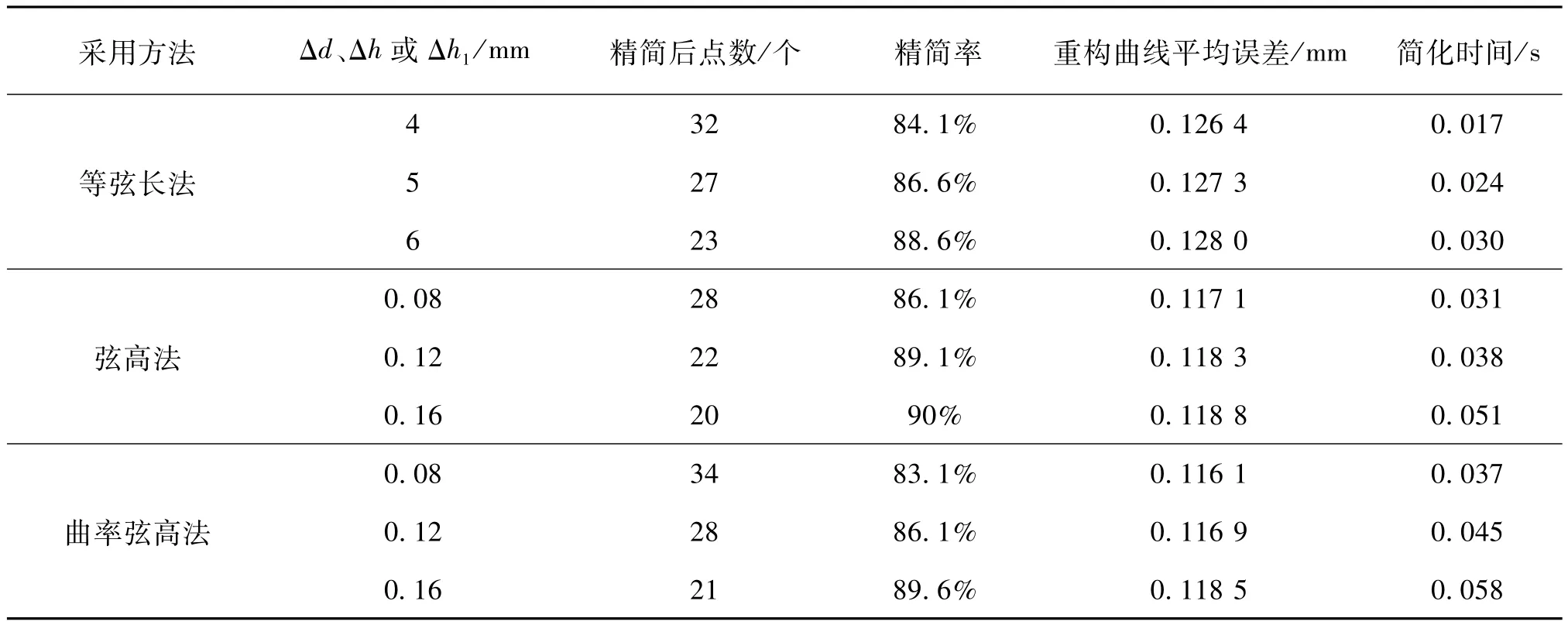
表1 正弦曲线点云简化数据

从图4和表1中可以看出，等弦长法可以对原始点云数据进行一定程度的精简，由于算法简单，在精简后点数相同时，所用时间最短，该方法在表面特征平缓、点云数据分布均匀的情况下简化效果较好，但在曲率变化较大的区域，会存在测量点精简过多而导致外形特征的缺失。弦高法与等弦长法相比，在处理曲率变化较大区域的测量点时，能更好地保留点云的外形特征。此外，在精简后点数相同的情况下，前者的重构精度平均误差要低于后者。该方法基本可以保证在曲率大的区域，测量点密集；曲率小的区域，测量点稀疏。但相邻点相距很远时，即使曲率变化很小，弦高也可能很大；而相邻点相距较近时，即使弦高很小，曲率变化也可能很大。因此，该方法可能会导致个别细节信息丢失的现象。曲率弦高法克服了这一缺陷，在弦高法的基础上加入了曲率参数，利用曲率的变化改变给定弦高值来简化点云数据，避免了个别细节信息因为仅依靠弦高约束而导致的丢失。该方法保留点云特征情况较好，但是算法复杂，精简率略高且简化时间略长。

图4 简化结果比较

4 应用实例

本文选取不同方法对视觉测量后的二次曲面（见图5）数据进行精简，二次曲面原始点云共有103 041个点，在要求平均误差小于0.2 mm时，用等弦长法精简后的点云数据保留了40 401个点（见图6），数据精简率为60.8%；用弦高法精简后的点云数据保留了19 673个点（见图7），数据精简率为80.9%；用曲率弦高法精简后的点云数据保留了10 517个点（见图8），数据精简率为89.8%。

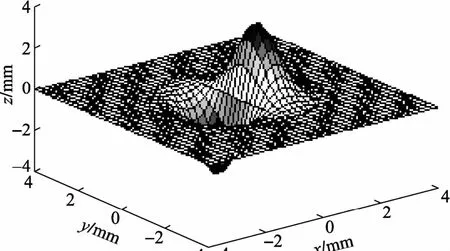
图5 初始二次曲面

从图8可以看出，采用曲率弦高法可以对视觉测量的数据点云进行较好的精简，精简率达到89.8%，在曲率较大的区域保留了较多的点云数据，在曲率较小的区域保留了较少的点云数据。

图6 等弦长法精简后点云

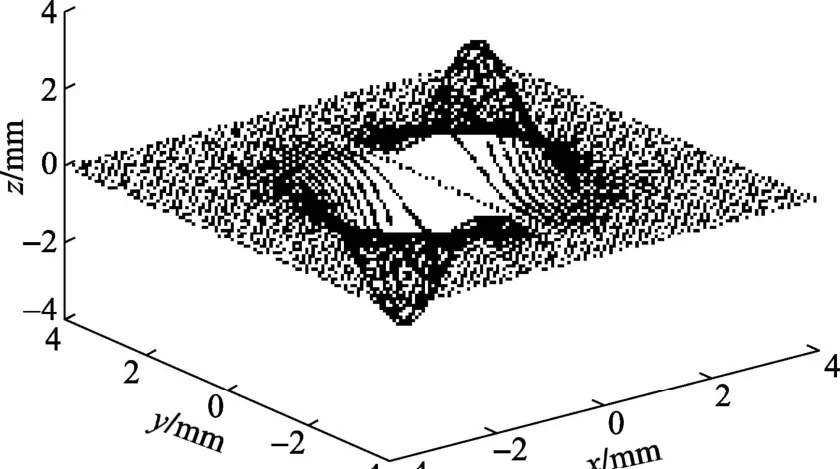
图7 弦高法精简后点云

5 结 论

本文提出基于曲率弦高法的点云数据简化方法，实现了海量测量数据的精简。该方法以构建的弦高函数为依据，采用相邻点之间的变化弦高作为是否进行测量点简化的判断标准，借助弦高法的数据精简原理确定需保留的测量点。由仿真实例可以看出，该方法在平均误差小于0.2 mm时，精简率为89.8%，能够对海量点云数据进行直接、有效的精简，并实现视觉测量的测点按曲面曲率合理分布。

图8 曲率弦高法精简后点云

］

［1］ 许智钦，孙长库，等.3D逆向工程技术［M］.北京：中国计量出版社，2002.

［2］ Zhu S P，Gao Y.Noncontact 3-D Coordinate Measurement of Cross-cutting Feature Points on the Surface of a Large-scaleWorkpiece Based on the Machine Vision Method［J］.IEEE Transactions on Instrumentation and Measurement，2010，59（7）：1874-1887.

［3］ 张玉存，付献斌，白旭东.一种大型锻件外形尺寸在线测量新方法［J］.计量学报，2010，31（5）：421-425.

［4］ 黄桂平，李广云，王保丰，等.单目视觉测量技术研究［J］.计量学报，2004，25（4）：314-317.

［5］ Lee K H，Woo H，Suk T.Data reduction methods for reverse engineering［J］.The International Journal of Advanced Manufacturing Technology，2001，17（10）：735-743.

［6］ Martin RR，Stroud IA，Marshal A D.Data reduction for reverse engineering［J］.Computer and Automation Institute of Hungarian Academy of Science，1996，1068：63-69.

［7］ 洪军，丁玉成，曹亮，等.逆向工程中的测量数据精简技术研究［J］.西安交通大学学报，2004，38（7）：661-664.

［8］ 张丽艳，周儒荣，蔡炜斌，等.海量测量数据简化技术研究［J］.计算机辅助设计与图形学学报，2001，13（11）：1019-1023.

［9］ 万军，鞠鲁粤.逆向工程中数据点云精简方法研究［J］.上海大学学报（自然科学版），2004，10（1）：26-29.

［10］ 李珂珍，娄小平，吕乃光.用于点云曲面重构的数据精简方法研究［J］.北京机械工业学院学报，2009，24（1）：17-20.

Massive Cloud Data Sim p lification Based on Curvature Hypotenuse-height Method

WU Feng-he， WANG Xin， SUN Ying-bing， WANG Jun
（College of Mechanical Engineering，Yanshan University，Qinhuangdao，Hebei066004，China）

In the field of vision measurement，the size of clouds data of the point which obtained in vision measurement process is so large that it is inconvenient to be calculated，stored and reconstructed.Based on the analysis of cloud data characteristics of vision measurement point，combined curvature principle with the chord height algorithm，a mass cloud data reducingmethod based on curvature chord heightalgorithm is presented.With thismethod，the function of the chord heightwas built considering the curvature variation of the curves，and the value of changing chord heightof each point is obtained by iteration，and then themeasurement points to be retained were determined based on the data reducing method of chord height algorithm.Simulation results showed that the cloud data reduced 89.8%through thismethod when the average error was less than 0.2mm.So the cloud data of mass points were reduced directly and effectively，and the reasonable distribution ofmeasurement point according to the curvature of the surface was realized.

Metrology；Visionmeasurement；Curvature；Chord height；Data reduction

TP92

：A

：1000-1158（2015）03-0229-05

10.3969／j.issn.1000-1158.2015.03.02

2013-07-24；

：2014-10-29

河北省自然科学基金（E2011203091）；高等学校博士学科点专项科研基金（20121333110011）

吴凤和（1968-），男，内蒙古扎兰屯人，燕山大学教授，博士生导师，主要研究方向为数字化测量与建模、数字化制造。risingwu＠ysu.edu.cn