外边界封闭内边界定压油气井模型求解及分析
2015-08-10姬安召崔建斌薛胥青王玉风
姬安召,崔建斌,薛胥青,王玉风,许 泰
( 1.陇东学院能源工程学院,甘肃庆阳 745000;2.陇东学院数学与统计学院,甘肃庆阳 745000)
1949 年Van Everdingen 采用拉普拉斯变换求解油气渗流数学模型, 为油气渗流数学模型求解引入新的方法[1]。 20 世纪60 年代初,Баренбдатт 建立了双重介 质 达 西 渗 流 的 数 学 模 型。 KazemiH.、OdehA.S.、WarrenJ.E.、Polalrd、陈钟祥、蒋继光等人研究了双重介质达西渗流[2,3]。 20 世纪末,葛家理、吴玉树等人对三重介质渗流特征进行了研究,刘慈群、刘曰武对表皮效应和井储效应模型的拉普拉斯空间解进行研究, 姚军等也对这类三重介质做了理论研究[4,5]。 2006 年李成勇对三重介质油藏模型及水平井试井解释方法进行研究[6]。2008 年张利军对双渗三重介质油藏试井分析方法进行研究[7]。但这些模型基本都是基于井底定产量条件来研究的,在实际现场,生产过程中可能会出现井底定压的情况, 针对井底定压生产情况研究较少,Van Everdingen 和Hurst 等人做了这方面的研究。笔者在前人研究成果的基础之上, 分别对油气井井底定压生产过程中渗流规律进行研究。
1 油井数学模型建立及求解
1.1 数学模型
模型假设[8]条件:储层中的渗流为单相( 油相)渗流;储层中流动的油相是微可压缩;储层为均质水平等厚;油相在地层中的流动服从达西定律;不考虑储层污染和井储效应。
为了研究问题的简便, 需要把某些有量纲的物理量进行无量纲化,即引进无量纲参数[8],具体无量纲参数定义如下:
无量纲压力:
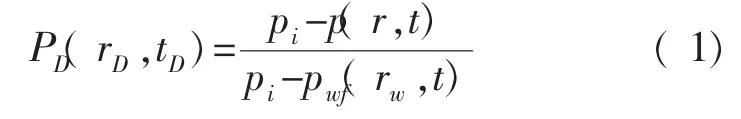
无量纲时间:

无量纲半径:

根据上述无量纲参数的定义, 可以得到圆形封闭地层中心有一口油井以恒定井底压力进行生产时无量纲化渗流数学模型如下:
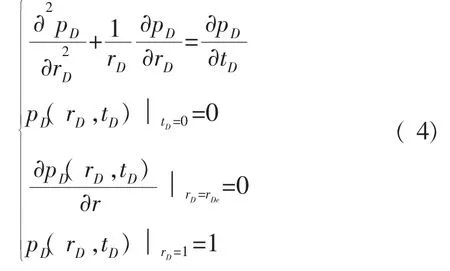
1.2 微分方程的求解
根据拉氏变换的定义[9]和拉氏变换微分定理性质,对( 4)式tD→进行拉氏变换。通过拉氏变换,将偏微分方程转换为二阶常微分方程, 方程为零阶变形的贝塞尔方程,其方程的通解[9]为:

根据贝塞尔函数的性质[9],再结合封闭外边界拉氏变换压力导数等于零和定压内边界拉氏变换等于1/可得系数A 和B:

将式( 6)代入( 5)式可得方程( 4)式的特解为:

1.3 压力反演
现在需要对拉氏空间的解进行反演, 按照反演的原则,首先需要确定被反演函数的奇点,由上式可以看出,其中一个奇点是=0,而其他奇点是和有关的。在>0 的正实轴上, 分母上的贝塞尔函数不会为零[8],只有在为负值,即=-u2时,分母中的函数变为带虚自变量的函数才有可能出现奇点。
根据贝塞尔函数的性质[9],对( 7)进行极限运算可得:

根据拉氏反变换的性质则有:


1.4 产量分析
为了得到油井产量的变化规律, 先求解井底无量纲压力梯度,对式( 11)进行求导可得式( 12)。
因为:

代入式( 13)可得:

故定义无量纲产量如下:

根据无量纲产量的定义,结合( 15)式,可得式( 16)。
其中:p-压力( 0.1 MPa);t-时间( s);k-渗透率( μm2);φ-孔隙度( 小数);r-半径( cm);h-储层有效厚度( cm);μ-粘度( mPa·s);ct-综合压缩系数(( 0.1 MPa)-1);Qo( t)-产量( 井下产量)( cm3/s);A-渗流面积( cm2);v,-渗流速度( cm/s)。

根据( 15)式,当无量纲产量计算精度设置为10-6时,则通过图1 可以看出,在压力波传播到边界以前,单井的产量不变,当压力波传播到边界以后,不同的供给边界,其产量的变化规律不一致,供给半径越大,其产量开始下降的时间越晚。

根据( 15)式,当无量纲产量计算精度设置为10-6时,则通过图2 可以看出,当无量纲半径越小,计算时所需的根越少;当无量纲时间越大,计算时所需的根越少。
2 气井定井底压力生产时常用工程单位下的产量表示
同油井模型建立及求解的方法一致, 可得气井定井底压力生产时在标况下的产量计算公式。

图2 无量纲半径、无量纲时间与复合贝塞尔方程根数量关系曲线

式( 17)为压力形式,式( 18)为压力平方形式,式( 19)为拟压力表示形式,根据式( 16),结合单位换算方法,可得式( 20)常用工程单位油井产量。
式中:p-压力( MPa);ψ-拟压力(( MPa)2/mPa·s);rw-井半径( m);t-时间( h);k-渗透率( mD);μ-粘度( mPa·s);h-地储层有效厚度( m);ct-综合压缩系数(( MPa)-1);Qo( t)-油井产量( 井下)( m3/d);Qgsc( t)-气井标况下的产量( 104m3/d)。
3 结论及建议
( 1)井底定压生产时,无量纲供给半径对无量纲产量的影响较大,不同的供给半径,其无量纲产量的变化规律不一致。
( 2)无量纲供给半径越大,无量纲时间越短,复合贝塞尔方程根的个数对无量纲产量的影响越大。
( 3)建议合理选择复合贝塞尔方程:Y1( rDeai)J0( ai)-Y0( ai)J1( rDeai)=0 根的个数,这样才能保证计算产量具有可靠性。
[ 1] Van Everdingen.The Application of the Laplace Transformation to Flow Problems in Reservoirs[ J]. Journal of Petroleum Technology,1949,1( 12):305-324.
[ 2] 蒋继光,等.裂缝性储集层内渗流间题的精确解[ J].力学,
1977,( 23):263-269.
[ 3] 蒋继光.裂缝性储集层内渗流问题的精确解Ⅱ[ J].应用数学学报,1980,3( 3):210-222.
[ 4] 吴玉树,葛家理.三重介质裂-隙油藏中的渗流问题[ J].力学学报,1983,( 6):643-650.
[ 5] 冯文光,等.多重介质组合油藏非定常非达西高速渗流问题的解析研究[ J].西南石油大学学报,1985,22( 3):14-28.
[ 6] 李成勇,刘启国,张燃,等.三重介质油藏水平井试井解释模型研究[ J].西南石油大学学报,2006,28( 4):32-37.
[ 7] 张利军,程时清,尹洪军.双渗三重介质油藏试井分析[ J].特种油气藏,2008,15( 5):66-73.
[ 8] 郎兆新.油气地下渗流力学[ M].北京:石油大学出版社,2001.
[ 9] 梁昆淼. 数学物理方法[ M].北京:高等教育出版社,2010.
