任意数值分频器的FPGA实现
2015-08-10郜继红荀延龙卢旭盛
郜继红,荀延龙,卢旭盛
(1.内蒙古工业大学 电力学院,内蒙古 呼和浩特 010051;2.内蒙古工业大学 信息学院,内蒙古 呼和浩特 010051)
FPGA是数字系统主流控制器之一,成为目前硬件设计的研究重点[1]。工程人员在数字系统的设计过程中,总会遇到各种各样数值的分频要求,比如偶数分频、奇数分频、半整数分频、小数分频等等,通常一些数字系统设计中,系统不仅对信号频率有要求严格,而且对占空比也有严格的要求。整数分频器的实现比较简单,可以采用标准的计数器或可编程逻辑器件得以设计实现。但0.5倍整数分频和等占空比的奇数分频实现起来就比较困难 ,小数分频和分数分频就更加困难难[2]。计数器构成的分频器,大多只能实现整数分频,或者只能实现半整数分频和奇数分频。而实现小数分频的多数是专用分频器,针对这一问题,本人首先设计了各种数值的分频器,然后增加一个控制模块,用拨码开关选择分频类型,即由拨码的二进制数确定是偶数分频、奇数分频、小数分频还是分数分频。各种数值分频器由控制模块决定其分频的工作状态,最后综合起来成为通用分频器。根据分频器分频原理,摸索出了一种简单的设计方法,设计了任意数值分频器。
1 偶数分频器的设计
偶数分频最易于实现,可以利用计数器实现[3-4]。假设要设计M=2N的偶数分频,当计数值计数到0到K-1时(K用于调节占空比),输出的电平为1,计数器的计数值K到2N-1时,输出的状态为0。计数器计数到2N-1时计数器复位为0。如此循环下去,便可实现占空比为K/2N偶数分频,这里M和K都是可调整的预置数,K调整占空比,M调节分频系数。图1中M取值是6实现的是6分频。即输出时钟频率是输入时钟频率的1/6。从图1的仿真结果可以看出k=3=m/2,输出时钟占空比为50%。

图1 CLKIN的6分频仿真结果Fig.1 Simulation results of 6 frequency divider
2 奇数分频器的设计
想要实现非50%占空比的奇数分频,比如实现占空比为20%(1/5)、40%(2/5)、60%(3/5)、80%(4/5)的分频器,我们可以采用类似于偶数分频的方案就可以实现。但如果要实现占空比为50%的奇数分频,就不能用偶数分频中所采用的方案了。占空比50%奇数分频实现起来会比较麻烦一点,这是因为计数值为奇数,前半个和后半个周期所包含的不是整数个输入时钟脉冲clkin的周期。实现的方法很多,这里介绍一种占用资源少的方法。例如对时钟脉冲CLKIN进行5分频,前半个周期包含2.5个clkin周期,后半个周期包含2.5个clkin周期。需要定义两个计数器,CNT1和CNT2,分别对输入时钟的上升沿和下降沿进行计数,当计数值为0~((n/2)-1)时,输出时钟信号进行翻转,同时给计数器一个时钟复位信号,下一个时钟的上升沿到来时,计数器重新开始计数,如此循环即可。计数器CNT1和CNT2计数方法完全一样,只是翻转边沿不同。然后把这两个计数值输入一个组合逻辑作或运算,CLKOUT=CNT1+CNT2。图2是CLKIN的5分频。
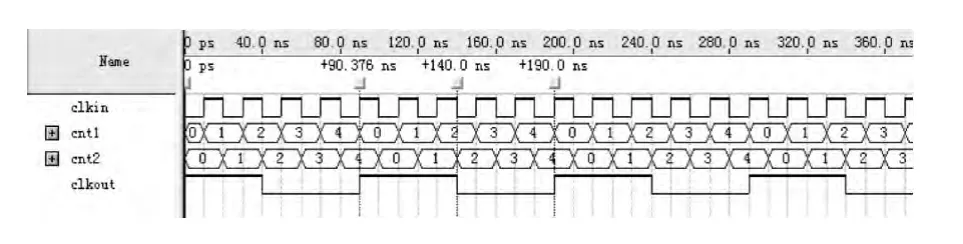
图2 CLKIN的50%占空比的5分频仿真Fig.2 Simulation results of 5 frequency divider for duty Ratio 50%
推广为一般方法:欲实现占空比为50%的2N+1分频器,则需要对分频时钟上升和下降沿分别进行1/(2N+1)分频,然后将两个分频所得的时钟信号作或运算便可得到占空比为50%的2N+1分频器[4]。
3 小数分频器的设计
实现小数分频器的方法很多,但其原理都基本一样,即通过可变分频和多次平均的方法得到[5-6]。本设计采用双模前置小数分频的方法设计。假设要进行m、n分频(m、n都是整数,且n<10),因为只有一位小数,所以总共要进行 10次分频,总的规律是进行n次m+1分频,10-n次m分频。假设要进行 k.mn分频(k、m、n都是整数且 m、n<10),由于小数是 2位,所以总共要进行100次分频,分频的规律是进行mn次k+1分频,100-mn次K分频。也就是说不管是几位小数总要进行两种系数的分频,两种分频究竟如何交叉进行,可以根据一定的规律计算出来,下面以2.7分频为例进行讲解。由上面的分析知道2.7分频要进行7次3分频,3次2分频。总分频值为:(7×3+3×2)/(7+3)=2.7,将小数部分 7 按倍累加,假设累加的值为A,如果A<10则进行2分频,A<10的话下一次则加上7,此后,如果A≥10则进行3分频,3分频过后再将累加值减去3后与10比较以决定下一次分频是7分频还是2分频,计算过程见表1。图3是2.7小数分频仿真波形。小数分频器部分VHDL核心代码如下:


表1 2.7分频计算序列计算值Tab.1 The value of 2.7 dividing calculation sequence
4 分数分频器设计

图3 2.7小数分频仿真波形Fig.3 Simulation waveform of 2.7 frequency divider
表2 分频规律Tab.2 The law of frequency divider

表2 分频规律Tab.2 The law of frequency divider
分频次数 累加值 分频系数1 7 2 2 14 3 3 11 2 4 18 3 5 15 3 6 12 2 7 19 3 8 16 3 9 13 2 10 10 2 11 17 3 12 14 3 13 11 2
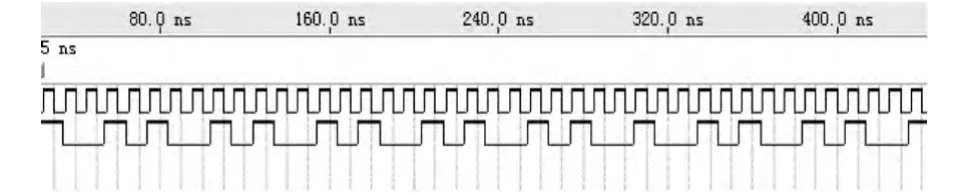
图4 33/13分频器仿真波形Fig.4 Simulation waveform of 33/13 frequency divider
5 多数值分频器的实现
将上述各模块整合在一起,需要增加一个控制模块,这样就构成了多数值分频器。顶层原理图见图5。

图5 任意分频器原理图Fig.5 Schematic diagram of any frequency divider
当B=00时,实现整数分频,当B=01时实现占空比50箛的奇数分频,B=10时实现小数分频,B=11时实现分数分频。其中M、K控制整数分频的分频系数以及占空比。小数分频时M、N分别调整整数部分和小数部分。分数分频时K调整整数部分,M,N调整分母和分子值,虽然预置端口较多,但可调整性很好。
6 结束语
文中给出了基于FPGA的多数值分频器的设计方法,设计采用自顶而下的设计方法,进行功能模块的划分,该分频器可以实现偶数、奇数、小数、分数的分频,有良好的可移值性,本设计选用EP2C5Q208C型FPGA芯片实现,从综合配置后的配置报告可以看出,本分频器占用FPGA资源很小。仿真结果和硬件测试结果验证了这个设计的有效性。对相关人员有一定的参考价值。
[1]张静亚.FPGA系统设计中资源分配的分析和研究[J].信息化研究,2009,35(3):37-39.
[2]王广义,赵卫华,赵艳秋.一种小数分频器的设计及性能研究[J].自动化技术与应用,2007,26(9):101-102.
[3]潘松,黄继业.EDA技术实用教程[M].3版.北京:科学出版社,2006.
[4]刘爱荣,王振成,陈扬,等.EDA技术CPLD/FPGA开发应用简明教程[M].2版.北京:清华大学出版社,2013.
[5]李炯.一种基于FPGA的任意分频器设计与实现[J].现代电子技术,2012,25(24):185-186
[6]黄守麟.基于FPGA的超高精度任意小数分频器的设计[J].计算机工程与应用,2008,(33s):485-487.
[7]周鹏,和卫星,匡敏驰,等.FPGA在PC-104系统I/O设备扩展中的应用[J].工业仪表与自动化装置,2013(2):50-53,72.
[8]程光伟,刘大伟.基于FPGA的异步FIFO的研究和设计[J].工业仪表与自动化装置,2013(2):67-69,75.
