基于振动信号的谱分析与综合评价
2015-08-10莫家庆吕小毅贾振红
俞 潇,莫家庆,吕小毅,贾振红
(新疆大学 信息科学与工程学院,新疆 乌鲁木齐 830046)
智能安防在生产生活中至关重要,为维护安全提供有力的保障。基于智能振动信号的谱分析是一种重要的周界安全防范技术。例如管道安全受到威胁而尚未造成损失时就及时发现入侵行为,因此这是急待解决的问题。功率谱密度是信号的频谱分析方法,该方法利用利用傅里叶变换,求出与时域描述相对应的频域描述从中找出信号频谱的变化规律,以达到特征提取的目的。但是该方法的缺点在于频谱泄露、混叠现象等。相对于非平稳信号,小波包频带能量分析则更加合理。通过相应频带里能量比例的变化,反映各频带里信号的能量,包括非平稳、非线性振动能量[1]。但是,该方法的缺点在于需要一定的先验知识,例如小波基、分解层数的选取。快速谱峭度作为信号滤波的方法用于特征提取,该方法于2006年由Antoni提出。谱峭度对非平稳信号中的瞬态成分具有很高的敏感性,因此常用于检测信号的冲击成分。但是,该方法的缺点在于分解尺度固定缺乏自适应性。
本文是利用3种谱分析方法对敲击信号进行分析和评价。这3种方法分别是功率谱密度分析、小波包频带能量谱分析、快速谱峭度分析。比较不同分析方法之间的优劣性为瞬态振动信号的识别提供良好的依据和指导意义。
1 实测数据
振动仪采样频率为80 000 Hz,一共采集到412 160个点的敲击数据。在不敲击的情况下采样得到的数据是噪声。噪声的强度分布在[-18 739,+14 929]。其中敲击一次的信号强度最小,该信号的强度范围分布在 [-287 076,+278 437]。因此振动仪采集的敲击信号强度与噪声强度比很高,不需要再做信号的降噪处理。如图1所示分别是噪声,敲击一次、两次、三次的原始信号。
2 快速傅里叶变换的功率谱密度原理及应用
如果信号可以看作是平稳随机过程,那么功率谱密度就是信号自相关函数的傅立叶变换。信号的功率谱密度当且仅当信号是广义的平稳过程的时候才存在。如果信号不是平稳过程,那么自相关函数一定是两个变量的函数,这样就不存在功率谱密度,但是可以使用类似的技术估计时变谱密度。f(t)的谱密度和f(t)的自相关组成一个傅里叶变换对。傅里叶分析的结果之一就是Parseval定理(Parseval's theorem),这个定理表明能量谱密度曲线下的面积等于信号幅度平方下的面积。具体算法参考文献[2]。

图1 噪声以及3种敲击信号Fig.1 Noise and three kinds of knock signal
由于振动仪采样频率过高,导致数据量大,冗余度增加,对时频分析带来了一定困难。考虑到时效问题以及在敲击信号不失真的前提下,提高图谱分辨率的同时,对敲击信号进行降采样,每20点采样一次,得到20 608个点。如图2所示经过FFT快速傅里叶变换后得到敲击一次、两次、三次信号的功率谱密度。
从图2中可以明显看出敲击一次信号的功率谱密度的峰值,在217 Hz出现了全谱的峰值。但是从图 2中无法看出敲击两次和三次信号的功率谱密度的峰值。假如在识别时需要特征提取,没有明显的特征也不知道对应的频率是多少,这样就失去了频谱分析的意义。从上面的图形以及分析可以看出FFT功率谱密度是无法正确反映瞬态信号的频谱特征。

图2 3种敲击信号的功率谱密度Fig.2 Three kinds of power spectral density of the knock signal
3 小波包频带能量谱原理及应用
小波包频带能量谱反映了信号的能量分布特征,相较于FFT频谱分析选取某些特征频率的幅值进行分析,小波包频带能量谱分析的是经过小波包分解以后各个频带信号的能量。各个频带能量相加原等于分解前的信号能量。该方法适用于非平稳、非线振动信号,如碰撞、摩擦等。所以,小波包频带能量谱分析更具有合理性。
在小波变换中,原始信号 f(x),在 L2(R)上的 2 范数定义为:

可见,信号的2范数的平方等价于原始信号在时域上的能量。如果基本小波φ(x)是一个允许小波,则存在

具体算法请参考文献[3]。

图3 3种敲击信号的小波包频带能量谱Fig.3 Three kinds of wavelet packet frequency band energy spectrum of the knock signal
经过多次实验选取小波基为db3进行四层小波包分解。第四层,16个频带分量的总能量为100,分布在16个频段内。如图3所示依次是敲击一次、两次和三次信号的小波包频带能量谱。根据敲击一次信号的小波包频带能量谱发现能量分别分布在高频段 1、2、4,相对应的能量占比为51.12、30.66、13.05;敲击两次的小波包能量占比分别分布在高频段1和2,占比为92.33和5.19;敲击3次的小波能量占比分布在高频段1和2,占比为84.66和10.00。这样根据能量占比情况可以分析出敲击一次与敲击两次、三次的区别最为明显。敲击两次与敲击三次区别不大但是也易于区分。
4 快速谱峭度原理及应用
Antoni对谱峭度进行了研究,文献[4-5]详细阐述了基于谱峭度的理论基础,正式给出了谱峭度的数学定义。在非平稳情况下,定义 y(t)为由信号 x(t)激励的系统响应,其 Wold-Cramer分解的频域表达式为:

式中:H(t,f)是系统的时变传递函数,表示 Y(t)在频率 f处的复包络。定义Y(t)的四阶谱累计量为:

式中:S2nY(f)是谱瞬时距,用来度量复包络能量,定义为:

将谱峭度定义为归一化累计量表示为:

这样一来就将谱峭度表征在(f,Δf)平面上,得到了峭度图。
为了获取基于谱峭度的最优滤波器的参数,将谱峭度作为STFT窗口宽度的函数提出了峭度图的概念。短时傅里叶变换谱峭度算法是将非平稳信号看成局部平稳信号所以不适用于瞬态信号并且计算中心频率和STFT窗口所有组合的峭度图费时又不便于工程的应用。因而出现了快速谱峭度图。该原理类似于离散小波包分解的算法,简单说就是两个准解析的低通滤波器和高通滤波器构成树状滤波器组结构。从检测的角度来看,存在一个最佳频率f和频率分辨率Δf的组合,使得谱峭度值最大[6]。在二维快速峭度图像中横坐标代表频率F,纵坐标则表示分解的层数 K,频率分辨率 Δf=2-(k+1)fs,图像上的颜色深浅表示不同Δf和f下的Sk值。具体算法参考文献[7]。
如图4所示最大分解层数为8层,采样频率为8 000 Hz。分别计算敲击一次、两次、三次的信号快速谱峭度得到一组最优滤波器参数。图中明显看出最深的颜色所对应的为最大谱峭度的层数。显然,为第1层。对应的中心频率为3 000 Hz,带宽为 2 000 Hz。

图4 3种敲击信号的快速谱峭度图Fig.4 Three kinds of fast spectral kurtosis of the knock signal
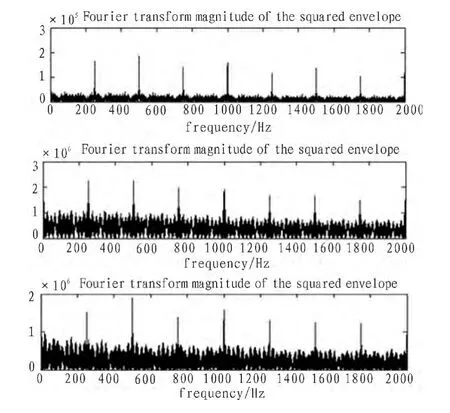
图5 3种敲击信号的平方包络谱Fig.5 Three kinds of square envelope spectral of the knock signal
如图5所示依次得到敲击一次、两次、三次信号的平方包络图。从平方包络图中可以清楚地看到瞬态信号明显增强,易于辨识。不同的敲击信号所对应的峰值不同,但是三幅包络图中第一次峰值的出现所对应的频率都为250 Hz。往后出现的都是该倍频所对应的峰值。这说明,无论敲击次数多少所出现的频率应该是一样的,应属于同一性质的振动信号。
5 结 论
在实际工程应用中,本文基于振动仪所采集的敲击信号进行了不同的谱分析。首先是基于FFT的功率谱密度分析,在不影响信息丢失的前提下对敲击信号进行降采样,分析得到的功率谱不能良好的反应非平稳信号的时频特征。再者利用小波包频带能量谱对敲击信号进行了分析,发现不同的信号能量大都集中在高频部分,而且在不同的频段能量占比不同。足以说明该方法可以分析信号能量特征有利于辨别信号。但是,该方法的缺点在于需要先验知识。最后利用快速谱峭度对敲击信号进行分析,发现该方法对于非平稳信号中的瞬态信号非常敏感,可以有效的提取出瞬态成分。快速谱峭度算法快速,准确,能够自适应选择带通滤波器参数,因此比起传统的滤波器构造过程,更加实用准确。
[1]毋文峰,王汉功,陈小虎.基于小波包能量谱-神经网络的液压泵故障诊断[J].液压与气动,2006(12):85-88.
[2]杨绿溪.现代数字信号处理[M].北京:科学出版社,2007.
[3]刘明才.小波分析及其应用[M].北京:清华大学出版社,2005.
[4]Antoni j.Randall R B.The spectral kurtosis:a useful tool for characterizing non-stationary signals[J].Mechanical Systems and Signal Processing,2006,20(2):282-307
[5]Antoni j.Randall R B.The spectral kurtosis:application to the vibratory surveillance and diagnostics of rotating machines[J].Mechanical Systems and Signal Processing,2006,20(2):308-311
[6]刘海洋.基于谱峭度的信号特征提取及其传动系统关键部件故障诊断应用[D].苏州大学,2013.
[7]Antoni j.Fast computation of the Kurtogram for the detection of transient faults[J].Mechanical Systems and Signal Processing,2007,21(1):108-124.
