基于改进鱼群寻优算法的天线阵方向图综合

黄 勇，玄晓波，姚凤薇，曹 扬

（上海无线电设备研究所 上海 200090）

在雷达和通讯等领域中，经常需要对阵列天线方向图进行特殊赋形设计。根据赋形条件求解出阵列的单元数目、空间排布、幅度相位分布等参数的过程，即为综合。阵列综合是一个复杂的多维非线性优化问题。当目标方向图比较复杂或者存在较多约束条件时，切比雪夫、泰勒等经典的解析方法就难以进行有效求解[1-2]，需要突破常规发展一种新的实现方法。

智能优化算法在解决全局性多目标优化问题时具有良好的适用性。近年来，在智能算法领域出现了一系列新颖算法，并作为解决传统复杂问题的一种新兴演化计算技术迅速成为了国内外的研究热点。目前，遗传算法[3-4]、差分进化算法[5]和粒子群优化算法[6]等智能算法已被应用到了天线领域，尤其是在阵列天线的优化设计方面。常规的智能优化算法虽然在深零陷生成和低旁瓣抑制上取得了良好的效果，但对于有着多零点和低旁瓣等多约束条件的阵列天线进行综合时仍难以避免早熟，易陷入局部收敛。

诞生于2002年的鱼群算法一种新颖的群体智能算法[7-8]，通过虚拟实现生物的视觉感官功能，模拟鱼类的觅食、群聚、追尾、随机等生物行为在搜索域中进行寻优，很适合解决天线阵列综合等复杂的多维非线性优化问题。针对传统算法容易陷入局部收敛的不足，本文提出了一种改进的鱼群寻优算法，将混沌优化算法和人工鱼群算法进行了结合，并将人工鱼的视野范围和步进设置成了动态调整，首次成功地将其应用于阵列天线方向图综合中，通过仿真验证了新算法的有效性。

1 改进的鱼群寻优算法简介

1.1 原始鱼群算法

人工鱼群算法通过模拟鱼群的觅食、聚群、追尾、随机等行为，且这些行为随机进行着互相转换，利用鱼群间的相互协作来找寻出问题最优解[7]。以求解极大值为例，假定鱼所在位置的食物浓度为f（X），鱼群算法的简要流程如图1所示。

1.2 改进的鱼群寻优算法

1.2.1 复合混沌映射

初始鱼群的个体分布状况直接影响着智能算法的计算准确性和全局收敛性。若初始鱼群分布性差，将导致算法收敛速度缓慢，甚至不收敛。在无法预知最优解存在区域的情况下，初始鱼群应尽可能地分散分布。混沌是一种普遍存在的非线性现象，混沌搜索具有内在随机性、初值敏感性、遍历性等特点。为确保初始鱼群的多样性，利用混沌序列来弥补智能算法初始值较随机的不足，借鉴文献[9]的思想，鱼群的初始化分别采用Logistic序列和Tent序列，其表达式分别如下式（1）、（2）所示：

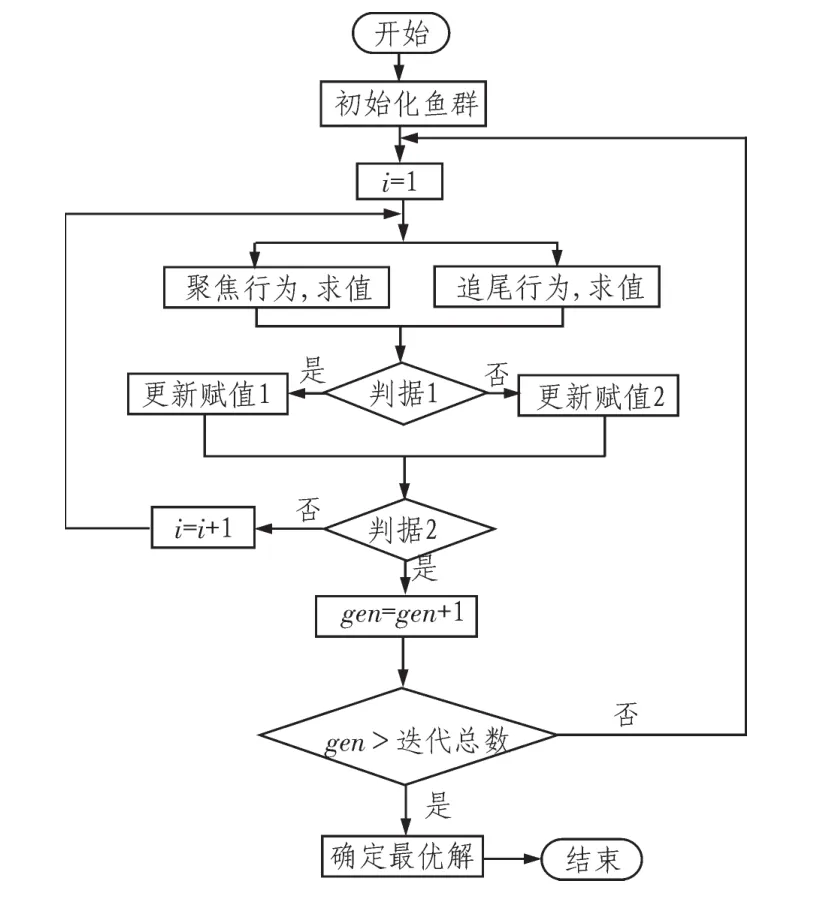
图1 人工鱼群算法流程图Fig.1 Flowchart of artificial fish swarm algorithm

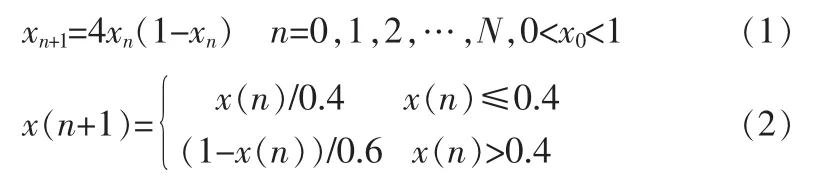
1.2.2 视野的动态调整

由群体智能算法的空间搜索机制可知，群体智能算法在计算早期应该着重于全局搜索，以保证较快的收敛速度和更广的搜索范围；在计算后期则应该着重于精细的局部搜索，实行局部搜索，以提高算法的求解精度。为符合Logistic模型的变化规律，借鉴粒子群算法中将惯性权重设置成动态变化的方法[9]，将鱼群算法中的视野范围也设置成动态变化的，其表达式如式（3）所示。

式中，k为迭代次数；vs为初始视野范围；ve为迭代至最大次数时的视野范围；M为最大迭代次数。随着迭代不断进行，视野范围v最近收敛于ve。

1.2.3 步进的动态调整

个体鱼移动步进越大，个体向最优位置靠近的速度越快，若在算法的早期采用较大的步进，收敛速度就越快，跳出局部最优的能力也就越强；反之，如果在算法的早期采用较小的步进，搜索范围小，收敛速度慢，且易陷入局部最优。同理，在算法的后期，在最优解搜索大致范围已确定的条件下，若采用较小的步进，可以提高算法的求解精度。动态步进的表达式为

式中，k为迭代次数；steps为初始步进；stepe为迭代至最大次数时的步进；a为衰减率。

2 阵列方向图综合

对于由N个理想点源组成的直线阵，以阵列的第一个单元为空间位置参考点，在不考虑单元之间耦合的条件下，天线阵列的远场方向图可表示为

式中，θ为空间辐射角，k为波数，dn为从第n个单元到第一个单元的距离（波长的倍数），An和an分别表示第n个单元的幅度和相位。

利用切比雪夫、泰勒等经典方法来实现超低副瓣综合存在着各种限制，需要突破常规发展一种新的方法。鱼群算法是通过虚拟实现生物的视觉感官功能，在搜索域中进行动态寻优，具有对初值不敏感、全局渐进收敛等优点，很适合用以天线方向图综合等复杂的多维非线性优化问题。用改进鱼群算法综合方向图的目的就是根据波束形状来求解阵列天线的激励幅度、相位和单元间距。适应度函数的设计是算法的关键，它的好坏直接决定了优化效果，它必须根据具体问题进行具体设计。对应线性阵列的综合，适应度函数采用文献中论述过的适应度函数[7]：

式中，MSLL和SLLdes为计算最大相对旁瓣电平和目标旁瓣电平；NULLθr是计算目标位置 θγ的零陷，NULLdes_θr是相应位置零陷深度值；NULL－STD表示多个零陷的方差，这是为了克服仅使用最高零陷深度作为优化项而导致的零陷不均衡现象；α、β和γ是各项指标的权值，T是需控制零陷深度的零陷总数。

采用20个天线单元组成的均匀直线阵来验证鱼群算法是否适合超低副瓣综合。所有单元相位相同，单元间距为0.6γ，副瓣低于－40 dB，所有的零陷深度不低于－70 dB，主瓣波束宽度不大于18°。综合所得的方向图和电流分布分别如图2和图3所示，鱼群算法寻优所得的最优方向图的各项指标参数均优于目标值。对鱼群算法和切比雪夫两种方法的综合效果进行了对比，相对于近似的电流分布，在波束宽度等大的条件下，通过鱼群算法综合所得的方向图副瓣更低。

鱼群算法除了可以实现超低副瓣方面外，还可以在副瓣、副瓣间差异、波束宽度、零陷等指标需要满足一定约束条件时对一特定角度范围内的副瓣进行抑制。若优化条件为所有单元相位相同，单元间距为0.6λ，副瓣低于－35 dB，主瓣波束宽度不大于 18°，30°～40°波束范围内的副瓣低于－70 dB，综合所得的方向图如图4所示。从图4可以看出，线阵方向图的副瓣和特定区域的零陷均达到了优化指标要求。

除了能实现常规的方向图外，鱼群算法还能实现特殊波束的赋形设计，如图5所示的余割波束赋形。进行此类赋形设计时，适应度函数一般选取赋形区、旁瓣区的目标函数和综合所得方向图两者间偏差的均方差来进行赋形设计。

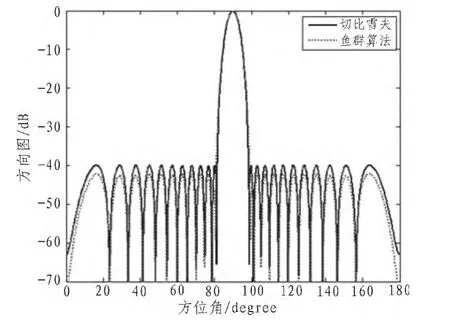
图2 20阵元均匀线阵归一化方向图Fig.2 Normalized power pattern for 20 elements with the same interelement spacing

图3 阵列归一化电流分布图示Fig.3 Normalized current value of the array

图4 30°～40°范围内具有低副瓣的方向图Fig.4 The pattern with low side-lobe between 30°to 40°

综上，通用鱼群寻优算法来实现超低副瓣抑制、零陷控制和特殊波束赋形设计是可行的，且比传统方法效果更优，运算的时效较传统算法有大幅度提升。

3 结束语

图5 余割平方波束赋形Fig.5 The pattern of Csc beam

针对传统智能算法在实现阵列方向图综合中存在早熟收敛，易陷入局部极值的缺陷，本文介绍了一种可以进行低副瓣抑制和波束赋形的新方法，即改进的鱼群算法。该算法将混沌算法和鱼群算法相结合，采用混沌序列初始化鱼群，以提高种群的多样性和搜索的遍历性，有效地避免了早熟收敛。为了在将算法早期的全局搜索和算法后期的精细局部搜索有机结合起来，借鉴粒子群算法中的动态惯性权重方法，将人工鱼的移动步进和视野范围均设置成动态变化的，以满足Logistic模型的变化规律。

为了验证算法的实用性和有效性，利用其进行阵列天线方向图综合和波束赋形设计。工程实例表明，该算法在解决多参数、非线性的复杂问题时具有良好的适用性。

[1]Robert C Hansen，Deng P.No-uniformly spaced super directive antenna arrays patel[J].IEEE， Antenna Array，2002，38（12）:131-135.

[2]Warnick，Jensen.Antennas and propagation for wireless communications[J].IEEE Transition on Antennas and Propagation，2001，49（13）:32-39.

[3]王宏建，高本庆，刘瑞祥.基于遗传算法的单脉冲阵列天线优化[J].中国科学工程，2002，4（5）:84-87.

[4]范瑜，金荣洪.基于一种新的遗传算法的天线方向图综合技术[J].电波科学学报，2004，19（2）:182-186.

[5]谢欢欢，杨伯朝.基于差分进化算法的阵列天线波束赋形研究[J].现代导航，2012，6（3）:219-224.

[6]齐美清，汪伟，金谋平.基于粒子群算法的天线阵方向图优化[J].现雷达科学与技术，2008，6（3）:231-234.

[7]王培崇，雷凤均，钱旭.改进人工鱼群算法及其收敛性分析[J].科学技术与工程，2013，13（3）:616-620.

[8]李晓磊，钱积新.基于分解协调的人工鱼群优化算法研究[J].电路与系统工程，2003，8（1）:1-6.

[9]刘建霞，李楠，谢克明.改进的思维进化算法在阵列天线综合中的应用[J].测试技术学报，2009，23（4）:331-336.