螺旋土钉钻进成孔扭矩分析
2015-08-10李智宁韩同春豆红强邱子义
李智宁,韩同春,豆红强,邱子义
(浙江大学 滨海和城市岩土工程研究中心,浙江 杭州310058)
螺旋土钉是将土钉加工成为带有螺旋叶片的杆体,将土钉直接旋入地层中,依靠螺旋叶片将土钉与地层联结成整体.该工艺省去钻孔和注浆工艺,可较大提高施工效率[1].但螺旋土钉材料全部采用钢材则造价较高,没有经济上的优势,因此目前对螺旋土钉的工程应用和相关研究较少.借鉴原理类似的螺纹桩和螺旋锚领域的工程应用和研究成果[2-6],结合螺旋土钉特点,本文将木塑复合材料(wood-plasticcomposites,WPC)引入螺旋土钉研究并分析螺旋土钉钻进成孔过程的扭矩.木塑复合材料是生物质与聚合物复合而成的新材料,具有木材和塑料的双重特性,如良好的加工和强度性能等,另外木塑复合材料的原料来源广泛、价格便宜、可回收再利用、经济环保[7].以上优点使木塑复合材料成为代替钢材作为螺旋土钉材料的首选.本文通过对自制螺旋土钉进行现场螺旋钻进试验,综合运用试验和解析方法,分析了各因素对螺旋土钉钻进成孔扭矩的影响,提出了螺旋土钉的尺寸优化意见以及适用土层.
1 螺旋土钉钻进成孔试验
1.1 试验装置
本次试验主要装置为自制螺旋土钉和测力计.
试验需自制螺旋土钉,土钉螺距l=10cm,螺纹宽度B=2cm,螺纹直径D=10cm,杆体直径d=8cm.由于螺旋土钉为手工制作,以上尺寸数据均为平均值,非精确值,每道螺纹略有不同.如图1所示为了螺旋土钉的尺寸.
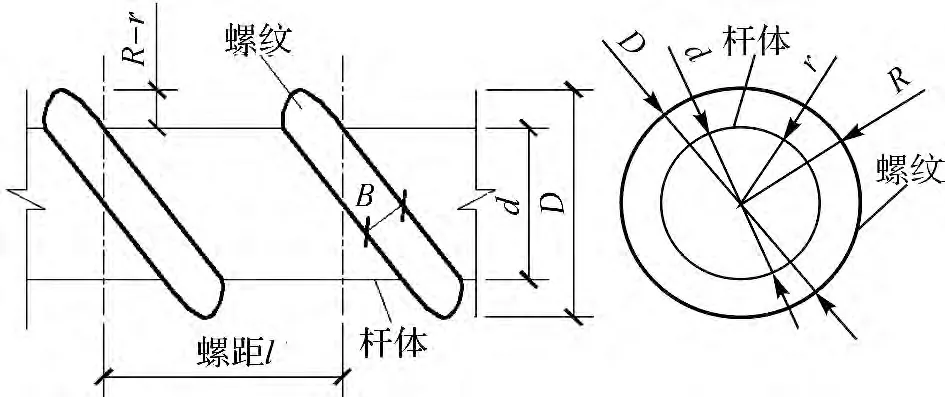
图1 螺旋土钉几何尺寸示意图Fig.1 Physical dimension of helical soil nail
由于木塑复合材料为合成材料,加工成指定尺寸的螺旋土钉需定制模具,试验成本大且耗时,本次试验自制的螺旋土钉由和木塑复合材料性能相近的硬木加工而成,如图2所示为试验用土钉.

图2 自制硬木螺旋土钉实物Fig.2 Helical soil nail witch made by hardwood
测力计采用双杰牌LTZ-100管型测力计,成孔扭矩采用间接测量方法,由于土钉匀速螺旋钻入土体时力矩平衡,测力计测得的拉力和力臂长度的乘积即为土钉钻入土体相应长度时的扭矩.
1.2 试验场地
由于本次试验螺旋土钉需人力钻入试验场地土层中,须选择较好的钻入的软土,因此试验场地就近选择在校内启真湖畔.为验证土钉在不同土质土层中的抗拔承载力差异,本次试验沿启真湖畔共选择2处试验场地:甲和乙试验场地均在启真湖岸边,但甲场地岸坡较缓,地势较低,见图3;乙场地岸坡较陡,地势较高.本次试验分别选取场地土样进行室内土工试验,测试了土的密度ρ、含水量w、黏聚力c和内摩擦角φ,见表1.

图3 试验场地情况Fig.3 Conditions of the test site
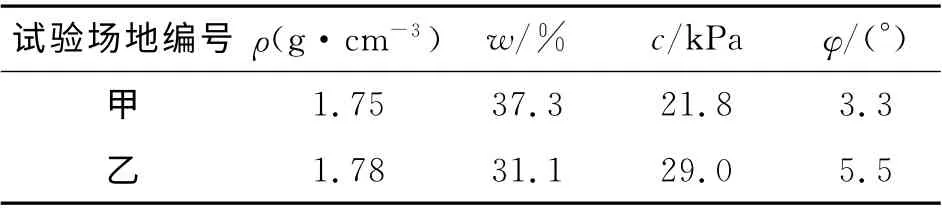
表1 土样试验成果汇总表Tab.1Summary of test soil
1.3 试验步骤
整套试验由2组对比试验组成:1)螺旋土钉不同入土长度的成孔扭矩对比试验;2)土钉在不同土质试验场地的成孔扭矩对比试验.
试验步骤:首先在甲场地进行人工钻孔,在入土长度δ=20、30、40、50cm 处分别测量成孔扭矩,因为螺旋土钉人工钻孔对表层土扰动较大,δ=20cm以下进行试验没有意义.由于在乙场地螺旋土钉40 cm 以上入土长度进行人工钻孔较困难,因此在δ=20、30、40cm 处分别测量成孔扭矩,方法和甲场地相同,具体见表2.
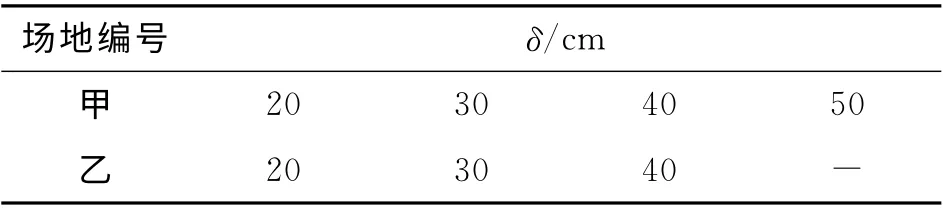
表2 现场试验钻孔编号汇总表Tab.2 Summary of drilling numbers
1.4 试验现象及成果
螺旋土钉钻进过程表层土易破坏,部分土体随着螺纹挤出孔口,土层越硬现象越明显,见图4.刚开始钻入土层时需要同时施加压力p 和扭矩M,当螺旋土钉钻入土层超过20cm 时,只需要施加扭矩,不需要压力也能继续钻入.测力计读数随入土长度增大而增大.相同入土长度,土层越硬测力计读数越大.换算后的试验扭矩成果见表3.

图4 表层土破坏情况Fig.4 Destruction of strata surface
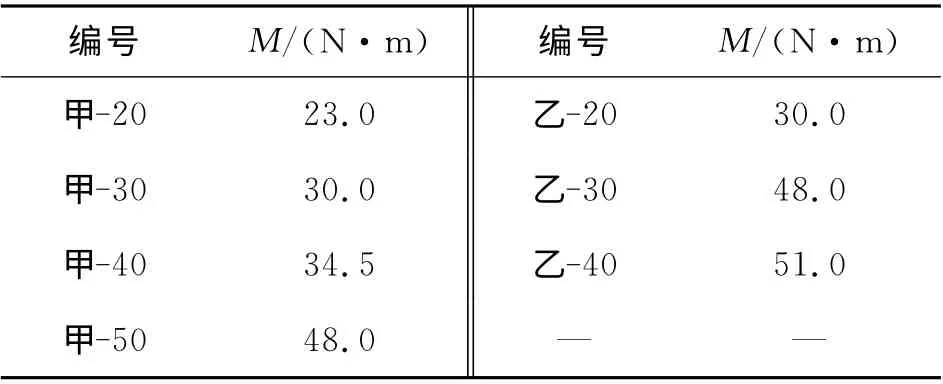
表3 现场试验螺旋土钉成孔扭矩成果表Tab.3 Results table of drilling torque
2 螺旋土钉钻进成孔扭矩解析表达
2.1 螺旋土钉受力特点
螺旋土钉通过沿土钉杆体形成的螺纹,使杆体和土之间力的作用形式由普通钻孔注浆土钉的摩擦力变为螺旋土钉的机械咬合力,改变了土钉抗拔的受力机理,极大地改善了土钉侧阻力作用.被加固土体滑动破坏时螺旋土钉的螺纹与土的机械咬合作用力构成滑动阻力,滑动产生的主要原因为螺纹根部土的局部挤压变形.与普通土钉不同,螺旋土钉旋入土层的过程中,镶嵌在土钉螺纹中间的土体和螺纹之外的土体之间的抗剪强度基本没有被破坏.当螺旋土钉达到抗拔承载力极限时,其破坏特征是以螺纹之间的土体剪切强度耗尽及达到了土的抗剪强度为特征,螺旋土钉与周围土体沿螺纹外径圆柱面上发生剪切滑移[4].本文主要研究螺旋土钉钻进成孔过程的受力情况.
2.2 螺旋土钉钻进成孔过程受力阶段划分
根据试验情况分析,螺旋土钉钻进成孔受力情况可分为2个阶段:1)刚开始钻入土层时需要同时施加压力p 和扭矩M;2)当螺旋土钉钻入土层一定长度时,只需要施加扭矩M,不需要压力p 也能继续钻入.因此必定有一个临界入土长度将2个阶段分界,见图5.
为了推导临界入土长度,本文对螺旋土钉钻进成孔过程中的受力情况做了如下假设:
1)假设土体和螺旋土钉表面的黏结强度qs为定值,而qs本质上是螺旋钻进过程中土钉表面受到周围土颗粒的摩擦力.
2)假设螺旋土钉匀速钻入土层,每钻进1个螺距长度时土钉旋转360o,钻进过程没有破坏螺纹间土体的抗剪强度.
3)由于本次试验螺旋土钉竖直方向钻入土层,底部钻头承受的土压力为相应深度的地基承载力.
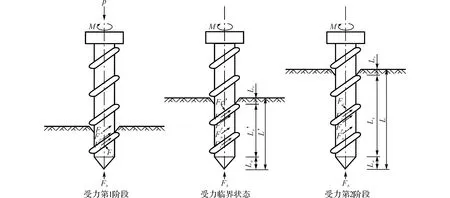
图5 螺旋土钉钻进成孔受力阶段Fig.5 Stage of forces on helical soil nails drilling into strata
4)WPC螺旋土钉质量较轻,其重力相比土钉受到的其他力很小.虽然本次试验螺旋土钉竖直方向钻入土层,但实际工程中土钉一般为近似水平向钻入土层.综上可忽略土钉重力影响.
由于摩擦力方向永远与物体运动方向相反,因此螺旋土钉表面受到土体的摩擦力方向与土钉横截面的夹角为β,由于不同半径的螺旋土钉横截面周长不同,因此β 是半径的因变量,记为β(ρ),其中r≤ρ≤R,见图6,其中图6(a)展开半径为R,图6(b)展开半径为r.
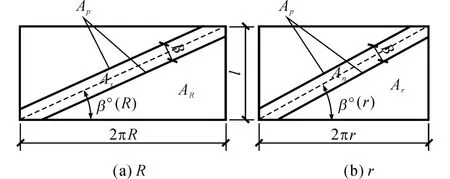
图6 1个螺距之间不同展开半径的螺旋土钉表面展开图Fig.6 Surface developed from different dimameters of helical soil nail between one pitch of screw thread
根据图6可确定如下几何关系:
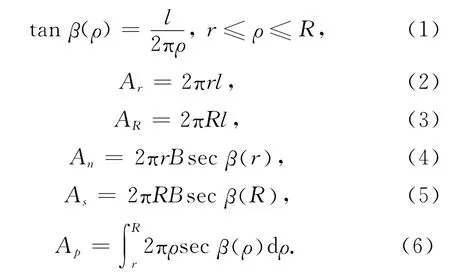
式中:R 为钻孔半径,即螺纹半径;r为土钉杆体半径;Ar为一个螺距之间半径为r的圆柱体表面积;AR为一个螺距之间半径为R 的圆柱体表面积;An为一个螺距之间的螺纹底面积;As为一个螺距之间的螺纹表面积;Ap为一个螺距之间的螺纹单边侧面积.
根据以上几何关系及黏结强度特点,可确定螺旋土钉表面受到的摩擦力:

式中:n 为螺距段数;Fn为土钉螺旋钻入过程中杆体表面受到的摩擦力;Fs为土钉螺旋钻入过程中螺纹表面受到的摩擦力;Fp为土钉螺旋钻入过程中螺纹侧面受到的摩擦力.
土钉螺旋钻入过程中端部受力情况见图7.

图7 螺旋土钉端部受力情况示意图Fig.7 Sketch of forces on top of helical soil nail
根据图7可确定圆锥形钻头表面积为

式中:α为1/2圆锥形钻头顶角.
根据以上几何关系可推导出土钉螺旋钻进过程中受到的端阻力为
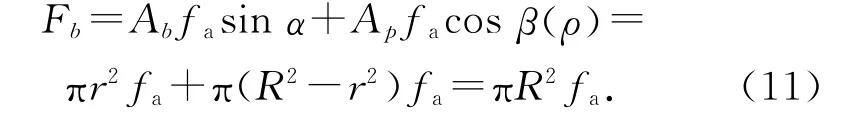
式中:fa为土钉钻进时端部受到的土压力.
2.3 螺旋土钉临界入土长度
根据图5所示螺旋土钉钻进成孔受力情况以及2.2节受力分析,将螺旋土钉表面受到的各项力分解为沿钻孔向外的分力,其合力为土钉螺旋钻进受到的阻力Fu.
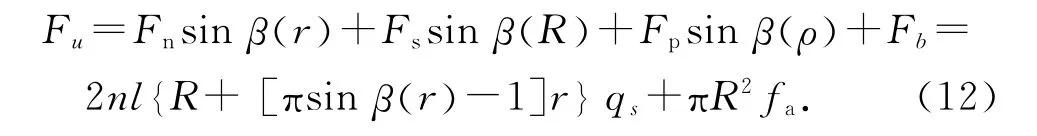
土钉螺旋钻进达到临界入土长度时,螺纹间土体受到Fu传递给螺纹外侧面施加的挤压力刚好达到极限平衡状态,此时螺纹间土体极限抗剪力为
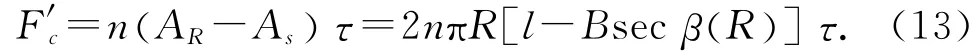
式中:τ为土层的抗剪强度.
F′c作用方向垂直于螺纹外侧面,如图5 所示,F′c分解为沿钻孔向内的分力为F′d.

螺旋土钉受力临界状态时F′d刚好抵消Fu,即F′d=Fu,联立式(13)和(15)可推出:
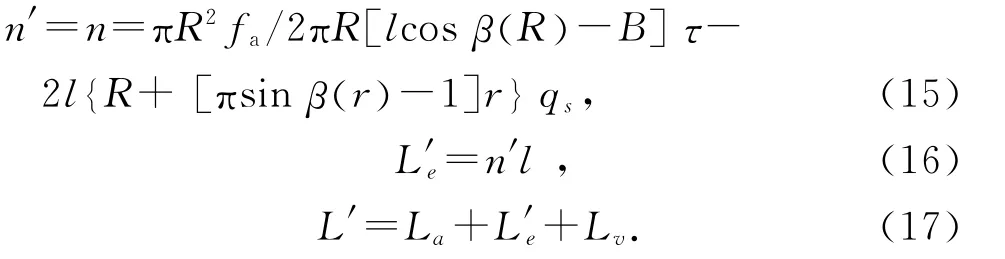
式中:n′为临界入土长度时土钉钻入土体的有效螺距段数;Le′为临界入土长度时土钉螺纹段钻入土体的有效长度,简称为临界有效长度;La为土钉钻头长度;Lv为土钉钻入过程中扰动钻孔表层土导致的失效螺纹段长度,简称为失效长度;L′为土钉的临界入土长度.
2.4 螺旋土钉钻进相应长度所需扭矩
土钉螺旋钻进超过临界入土长度后,只需要施加扭矩,螺纹间土体抗剪强度提供的沿钻孔向内的合力足够保证土钉继续钻入,此时螺纹间土体抗剪强度已经不需要全部发挥出来,因此土钉螺旋钻入过程中螺纹间土体抗剪力已经不能通过土体极限平衡状态进行计算,只能通过力的平衡关系间接计算.
土钉螺旋钻入时保持匀速,作用在土钉上沿钻孔向内的合力Fd等于沿钻孔向外的合力Fu:
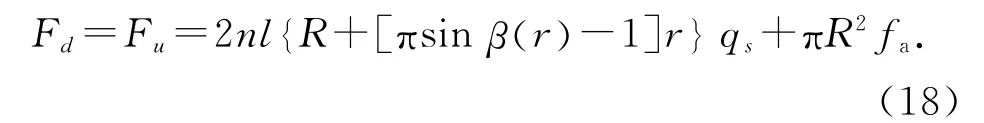
将土钉螺旋钻进过程中承受的各项力通过几何关系换算成垂直土钉中轴线的力分量,见图8.

图8 螺旋土钉钻进扭矩计算示意图Fig.8 Sketch of torque on helical soil nail
根据土钉匀速螺旋钻进时力矩平衡,垂直土钉中轴线各力分量和力臂相乘后取和,即得到土钉钻进相应长度所需扭矩为
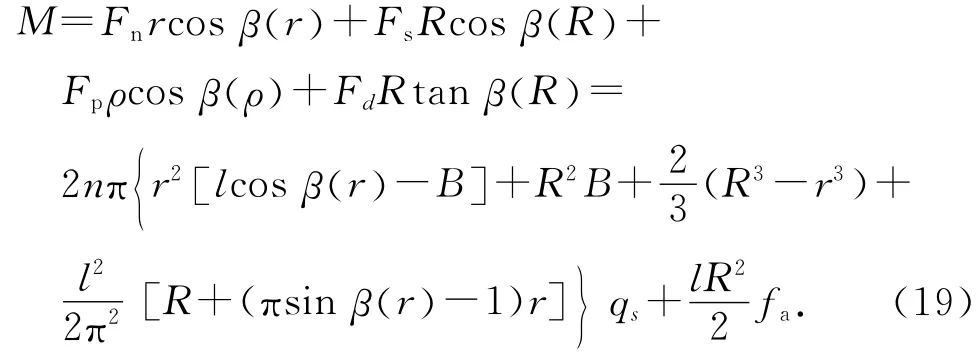
根据式(19)分析,土体对土钉螺旋钻入过程中的抗扭矩可分为2部分:1)由土体和螺旋土钉表面的黏结强度产生,即钉侧抗扭矩;2)由土钉端部承受的土压力fa产生,即钉端抗扭矩.
3 螺旋土钉钻进成孔过程分析
3.1 fa 和qs 的确定
本次试验螺旋土钉竖直方向钻入土层,土钉端部承受的土压力fa为相应深度的地基承载力.由于条件限制,本次试验没有直接测定土钉各入土深度处的地基承载力,采用间接测定方法.
由于土钉匀速螺旋钻进过程中端部的下压力和地基承载力保持平衡,而地基承载力相当于使地基开始发生局部剪损,但是极限平衡区尚未得到扩展时的临塑荷载pcr
[8],因此fa数值上等于pcr.
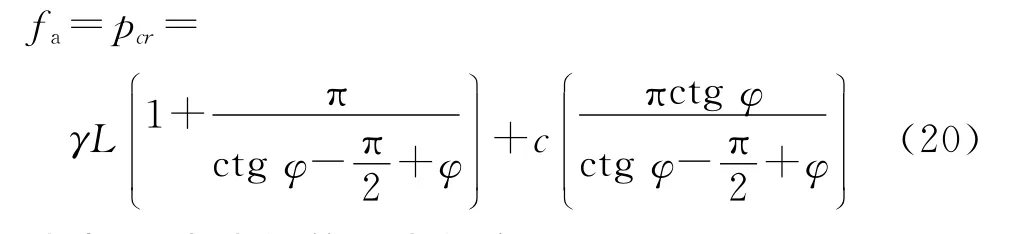
式中:L 为土钉的入土长度.
土层的平均重度、黏聚力c和内摩擦角均可通过室内试验测得,见表1,则fa可求.
扭矩M 通过现场试验测定已知,见表3,土体和螺旋土钉表面黏结强度可通过式(19),采用逆向推导的间接方法测定.经过计算,甲试验场地约为5.5kPa,乙试验场地约为10.0kPa.
3.2 有效入土长度对螺旋土钉钻进扭矩的影响
确定fa和qs后,可根据式(19)分析有效入土长度Le对螺旋土钉钻进扭矩的影响.
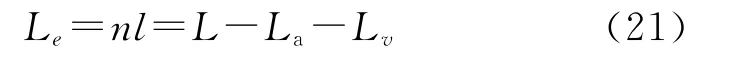
图9显示了螺旋土钉钻进扭矩M 及单位长度有效扭矩M′和Le的关系,相关参数见表4.


表4 M′和M 与Le 关系相关参数表Tab.4Parameters of M′&M ~Le
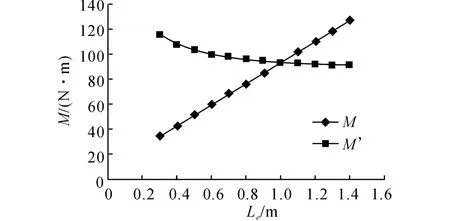
图9 M′和M 与Le 的关系曲线Fig.9 Curve of M′&M ~Le
M 随着Le的增大而增大,M′随着Le的增大而减小.分析其原因,由于土体对土钉螺旋钻进过程中产生的扭矩分为钉侧抗扭矩和钉端抗扭矩2部分,根据式(19),钉侧抗扭矩随着有效入土长度的增大而线性增大,单位长度土钉承受的钉侧抗扭矩不变.根据式(20),土钉端部承受的土压力fa分为2 部分,其中由土体黏聚力c提供的地基承载力和入土长度L 没有关系,因此L 越大,单位长度分担的fa越小,单位长度土钉承受的钉端抗扭矩反而减小.虽然M′随着Le的增大而减小,但是减小幅度越来越小,逐渐接近单位钉侧抗扭矩.
3.3 螺距对螺旋土钉钻进成孔过程的影响
如图10所示为M 及M’和距径比η 的关系.图11显示了临界有效长度Le’和距径比η 的关系.图10和图11关系曲线相关参数见表5.


表5 螺旋土钉钻进成孔过程和η 的关系相关参数表Tab.5 Parameters of drilling process versusη
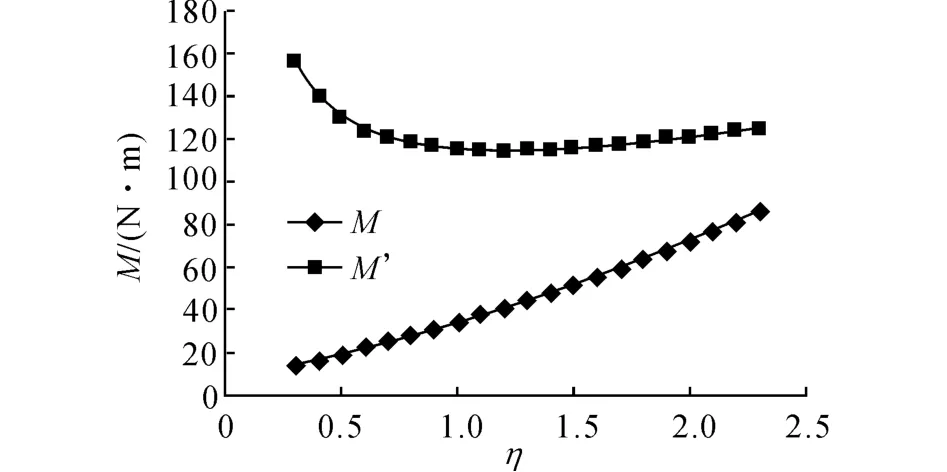
图10 M′和M 与η 的关系曲线Fig.10 Curve of M′&M ~η
M 随着η 的增大而增大,M′随着η 的增大先减小后缓慢增大.分析其原因,距径比η 越大,相同条件下土钉的螺纹越稀疏,螺距越长,土钉的有效入土长度也越长,根据式(19),扭矩M 越大.相反距径比η越小,相同条件下土钉的螺纹越密,土钉和周围土颗粒的接触面积越大,钉侧抗扭矩越大,从而导致单位长度有效扭矩M′越大;当距径比η 逐渐增大时,由于单位长度上螺纹段数逐渐减少,螺纹与土钉横截面的夹角β(R )逐渐增大,虽然单位长度钉侧抗扭矩趋于稳定,但是单位长度钉端抗扭矩却有增大趋势,从而导致单位长度有效扭矩M′先减小后缓慢增大.因此距径比η存在最优值,本例η=1.2时M′最小,根据李志毅等[9]研究成果,螺距大小对钻头所需成孔扭矩有重要影响,且螺距范围在成孔直径附近时所需成孔扭矩最小,本文结合试验和解析方法,推导出和数值模拟方法相似的结论.
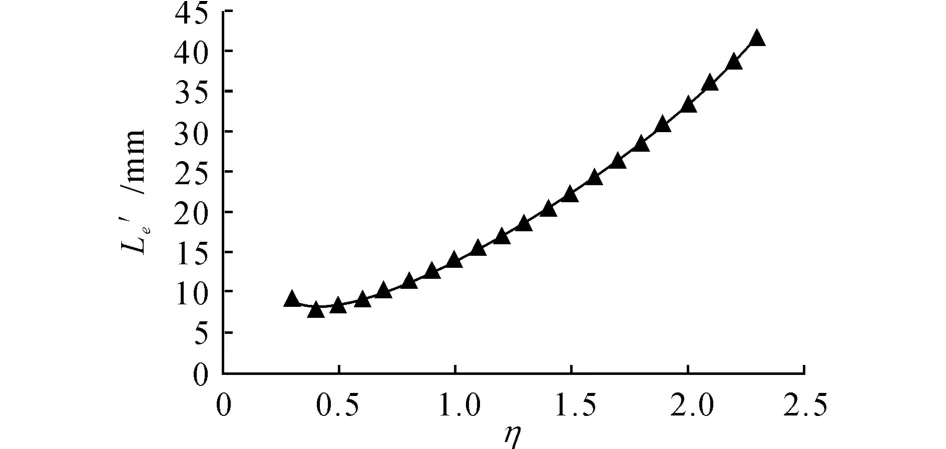
图11 Le′和η 的关系曲线Fig.11 Curve of Le′~η
Le′随着η 的增大先缓慢减小后持续增大.分析其原因,距径比η 越大,螺纹越稀疏,螺距越长,β(R )越大,根据式(14),F′d越小,因此需要土钉钻入土体的L′e更大.但是当η 过小,螺纹过密,由于螺纹有一定宽度,导致夹在螺纹间土体的面积过小,单位长度螺纹间土体抗剪力不足,因此也需要土钉钻入土体的L′e更大.螺纹过密对L′e的影响较小,实际也不会将螺纹加工过密,因此可认为L′e随着η 的增大而增大.
3.4 螺纹相对厚度对螺旋土钉钻进扭矩的影响
杆体直径d 和螺纹直径D 的比值ζ 间接反映螺纹的相对厚度h,ζ可称为杆径比.
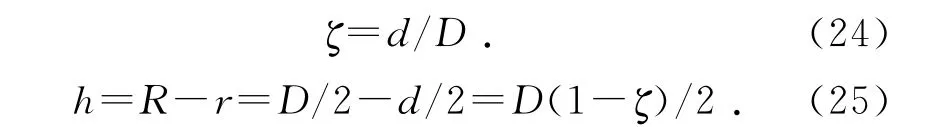
图12显示了M 及M′和杆径比ζ 的关系,相关参数见表6.

表6 M′和M 与ζ 关系相关参数表Tab.6Parameters of M′&M ~ζ

图12 M′和M 与ζ 的关系曲线Fig.12 Curve of M′&M ~ζ
M 和M′均随着ζ 的增大而增大.分析其原因,杆径比ζ越大,相同条件下土钉杆体表面积越大,杆体半径r即力臂也越大,因此钉侧抗扭矩越大,导致M 和M′同时增大.为减小抗扭矩,应减小杆径比,但是杆体直径过细会不满足土钉抗拉强度要求,因此螺旋土钉型式优化时应在满足设计抗拉强度的前提下尽量减小杆径比.
3.5 螺纹宽度对螺旋土钉钻进成孔过程的影响
图13显示了M 及M′和螺纹宽度B 的关系.图14显示了Le′和B 的关系.图13和图14关系曲线相关参数见表7.
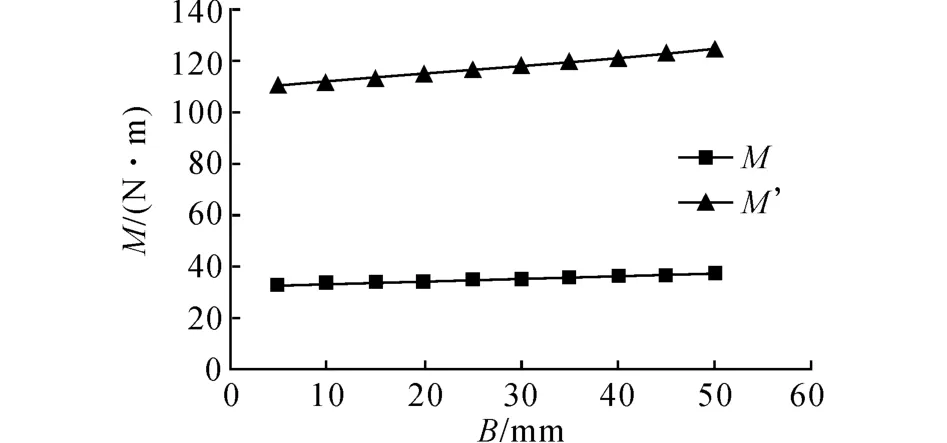
图13 M′和M 与B 的关系曲线Fig.13 Curve of M′&M ~B

表7 螺旋土钉钻进成孔过程和B 的关系相关参数表Tab.7 Parameters of drilling process versus B
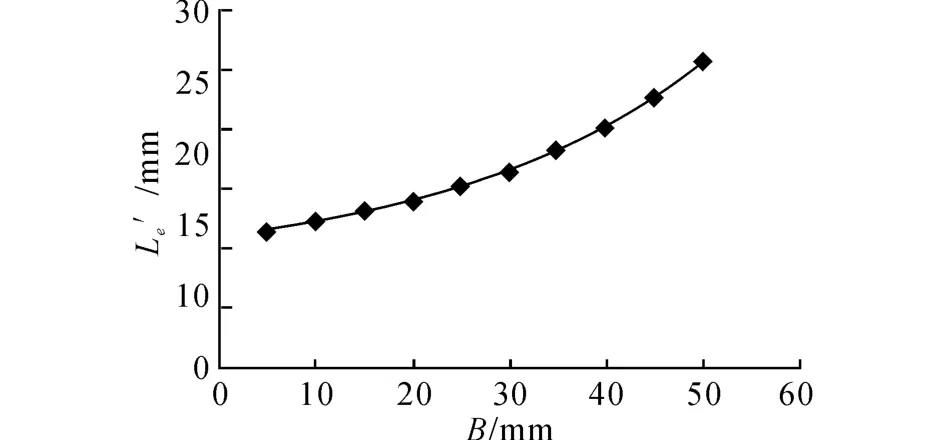
图14 Le′和B 的关系曲线Fig.14 Curve of Le′~B
M、M′和临界有效长度Le’均随着螺纹宽度B的增大而增大.分析其原因,螺纹宽度B 越大,相同条件下螺纹表面积越大,由于螺纹表面摩擦力力臂R 比杆体表面摩擦力力臂r 大,因此钉侧抗扭矩有所增大,导致M 和M′同时增大.螺纹宽度B 越大,相对夹在螺纹间土体的面积越小,因此需要土钉钻入土体的临界有效长度Le’越大.为减小抗扭矩,应减小螺纹宽度,但是螺纹需满足本身的强度要求,因此螺旋土钉型式优化时应在满足螺纹本身强度的前提下尽量减小螺纹宽度.
3.6 地质条件对螺旋土钉钻进成孔过程的影响
表8显示了不同地质条件对螺旋土钉钻进成孔过程的影响.相同条件下,地质条件越好、土质越硬,螺旋土钉钻入扭矩M 及单位长度有效扭矩M′越大;虽然土钉螺旋钻入过程中螺纹间土体抗剪强度提供的沿钻孔向内的合力越大,但是钉侧和钉端抗扭矩也越大,因此土钉钻进临界有效长度Le′差别不明显.
4 结 论
对影响螺旋土钉成孔扭矩的因素进行综合分析,得到如下结论:
(1)螺旋土钉开始钻入土层时需要同时施加压力和扭矩,当螺旋土钉钻入土层达到临界有效长度时,只需要施加扭矩,不需要压力也能继续钻入.
(2)螺旋土钉钻入扭矩和有效入土长度、螺纹宽度、直径和螺距有关.效入土长度和螺纹宽度越小则扭矩越小;杆体直径越小,螺纹直径越大,螺旋土钉钻入扭矩越小;螺距略大于螺纹直径时所需成孔扭矩最小.
(3)地质条件越好、土质越硬,螺旋土钉钻入扭矩越大,成孔越困难,因此螺旋土钉适用于土质较软的淤泥及淤泥质土.
由于木塑复合材料强度远不及钢筋,也不及岩石,并且强度随时间衰减,因此木塑复合材料螺旋土钉适用于基坑边坡支护等临时性工程,工程项目使用寿命结束后,一般打桩机械均可以在土钉加固区正常使用,不影响土地利用.在滨海或者滨湖地区,表层土往往是填土或者其他较硬的黏土,而其下往往是深厚的淤泥质土或者淤泥土层.在这种地层条件下进行基坑开挖,面临两类性质差异显著的土层,而且往往伴随着高地下水位,普通土钉在含水量大且低强度的软土中很难成孔,因此直接钻进成孔的螺旋土钉会有很大的工程应用前景.

表8 不同地质条件螺旋土钉钻进成孔成果表Tab.8 Results table of drilling process under different geological conditions
(
):
[1]程良奎,李象范.岩土锚固·土钉·喷射混凝土—原理、设计与应用[M].北京:中国建筑工业出版社,2008:533-542.
[2]李家华,窦德功,鲁子爱.螺纹桩负摩阻力计算方法[J].科学技术与工程,2012,12(25):6369-6372.LI Jia-hua,DOU De-gong,LU Zi-ai.Calculation and research on negative skin friction resistance of screw pile[J].Science Technology and Engineering,2012,12(25):6369-6372.
[3]窦德功,鲁子爱.螺纹桩承载性状分析与研究[J].水运工程,2012,4:32-35.DOU De-gong,LU Zi-ai.Bearing behavior of screw pile[J].Port&Waterway Engineering,2012,4:32-35.
[4]孙文怀,张元冬,魏厚峰,等.螺纹桩在软弱地层中的应用[J].华北水利水电学院学报,2009,30(3):74-76.SUN Wen-huai,ZHANG Yuan-dong,WEI Hou-feng,et al.Application of screw pile in weak strata[J].Journal of North China Institute of Water Conservancy and Hydroelectric Power,2009,30(3):74-76.
[5]NIROUMAND H,KASSIM K A,NAZIR R,et al.Systematic review of screw anchors in cohesionless soils[J].Soil mechanics and Foundation Engineering,2013,50(5):212-217.
[6]WANG D,MERIFIELD RS,GAUDIN C.Uplift behaviour of helical anchors in clay [J].Canadian Geotechnical Journal,2013,50(6):575-584.
[7]金林轶.复合木塑材料与现代设计[J].中国科技博览,2013,7:260.JIN Lin-yi.Wood plastic composite and modern design[J].Chinese Journal of science and Technology Expo,2013,7:260.
[8]陈仲颐,周景星,王洪瑾.土力学[M].北京:清华大学出版社,1994:278-294.
[9]李志毅,刘钟,赵琰飞,等.螺旋挤土桩钻头优化分析[J].同济大学学报:自然科学版,2011,39(8):1145-1149:278-294.LI Zhi-yi,LIU Zhong,ZHAO Yan-fei,et al.Optimization analysis on drill Auger of soil displacement screw pile[J].Journal of Tongji University:Natural Science,2011,39(8):1145-1149.
