基于水泥水化的早龄期混凝土温湿耦合
2015-08-10杜明月金南国王宇纬金贤玉
杜明月,田 野,金南国,王宇纬,金贤玉
(浙江大学 建筑工程学院,浙江 杭州310058)
早龄期混凝土在水化过程中发生物理化学反应将生成大量的水化产物、释放可观的水化热并消耗一定量的水分,使凝胶材料的化学成分及微观孔结构发生变化,从而改变混凝土的扩散性能(温度、湿度、氯离子、CO2等)[1-2].早龄期混凝土的温湿度不均匀扩散会导致不均匀变形,甚至引起混凝土的开裂,这也将影响混凝土后期强度的发展和对侵蚀性离子的抵抗能力.因此早龄期混凝土温湿度研究对分析混凝土结构的力学性能及抗腐蚀性能具有重要意义,也是混凝土结构耐久性研究的基础.
近年来,Smilauer等[3]基 于CEMHYD3D 微 观模型结合有限元方法研究了宏观热传导问题.Maekawa等[4]建立了DuCOM 微观粒子水化模型,并根据水泥颗粒形貌变化推导出混凝土有关传输性能的参数,进而应用到混凝土水分、侵蚀离子的传输过程中.但这些研究只是针对单一的混凝土温度场或湿度场,研究表明早龄期混凝土的温湿扩散特性具有明显的耦合 效应[5].因此Cervera等[6]、Gawin等[7]基于水泥水化动力学模型来研究温湿耦合扩散特性.虽然他们建立的模型易于耦合求解,但是水化动力学模型的参数均需通过试验确定,仍未能从水化过程的本质上解决早龄期混凝土温湿度场的耦合问题.
在水泥水化模型的基础上[8],本文考虑粉煤灰对水泥水化进程的影响,提出改进的掺矿物掺合料水泥水化模型,得出了水化度、水化速率和孔隙率等联系微观结构和宏观温湿度场的参数,进而将其引入到混凝土温湿扩散方程中建立了早龄期混凝土温湿度耦合作用分析模型.并通过已有试验数据对模型进行了验证.
1 水化模型
1.1 水泥水化微观结构模型
假设水泥颗粒为球状,水泥颗粒与相应的水构成一个边长为L 的正方体水化单元[9],水化反应仅发生在水化单元内部.水泥水化单元的体积由水胶比w/b决定.水泥水化过程的三维演变如图1所示[9-10].
水泥水化分为3个阶段.第1阶段,水泥与水搅拌在一起,水泥颗粒分布在水泥净浆之中,如图1(a)所示,水泥颗粒之间未相互接触.随着水化进程的发展,水泥水化产物不断生成,水泥颗粒的外半径不断增大,水泥颗粒的外径将达到并超过水化单元的边长L,进入水化第2阶段,如图1(b)所示.此时,不同粒径的水泥颗粒将互相接触并连接在一起,降低了水泥颗粒与水的接触面积,减缓了水泥水化进程[11].随着水化反应的进一步发展,如图1(c)所示,水化单元相邻面开始接触,反应速率将变得很慢.
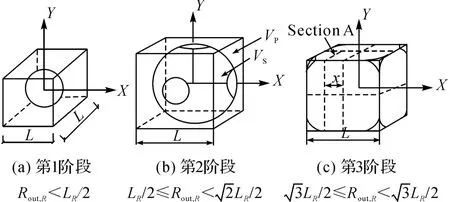
图1 水泥水化三维微观结构简图Fig.1 3D micro-structure diagram of cement hydration process
1.2 纯水泥水化模型
水泥水化程度可表示为水泥放热量与水泥最终放热量之比,假设水泥矿物组分在水泥颗粒中均匀分布,水泥颗粒放热量与颗粒的体积成正比[8,12],则初始半径为R0的水泥颗粒的水化程度αRc可表示为
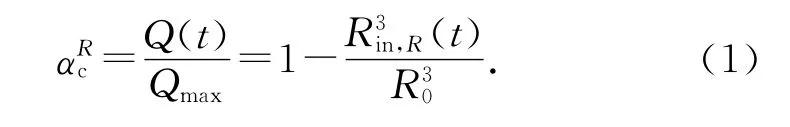
式中:Q(t)为水泥颗粒t时刻反应放出的热量;Qmax为水泥颗粒完全水化放热量;Rin,R(t)为初始半径为R0的水泥颗粒在t时刻的内半径.
Krstulovi等[13]提出水泥水化反应进程分为结晶成核反应、相边界反应、扩散反应3个基本过程.将式(1)代入Krstulovi-Dabi水泥水化反应公式,可以得到单位时间水泥水化的颗粒半径变化量:
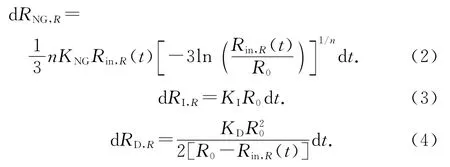
式中:dRNG,R、dRI,R、dRD,R分别为 初始半 径 为R0的水泥颗粒水化过程结晶成核反应、相边界反应、扩散反应半径减小量的绝对值;n 为与水泥矿物组分有关的常数;KNG、KI、KD分别为结晶成核反应速率常数、相边界反应速率常数、扩散反应速率常数.
根据最小耗能原理,水泥水化的颗粒半径理论变化速率dRtheoryin为

1.3 掺粉煤灰水泥的水化模型
掺粉煤灰水泥的水化由水泥水化与粉煤灰水化2部分组成.假设粉煤灰颗粒具有同水泥颗粒一样的微观水化单元[12,14],其水化动力学过程同样由3个方程分别控制,即结晶成核过程、相边界过程和扩散过程.则粉煤灰水化度αRf的计算公式同式(1)~(5),但是粉煤灰与水泥水化过程的反应常数KNG、KI、KD、n各不相同.
粉煤灰的掺入会影响水泥水化进程,包括粉煤灰的稀释效应、物理效应等[12,15],参考文献[12],考虑粉煤灰影响的水泥水化度为
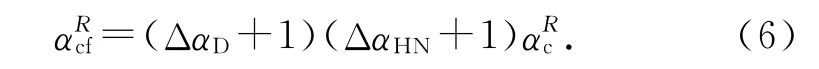
式中:ΔαD为粉煤灰的稀释效应导致的水泥水化度增大值;ΔαHN为粉煤灰的物理加速效应导致的水泥水化度增大值.
在实际水泥水化过程中,水分减少、孔隙饱和度、温度、水泥和水接触面积、粉煤灰等因素都影响着水泥颗粒半径变化速率.参考文献[12],修正的水泥颗粒半径变化速率为
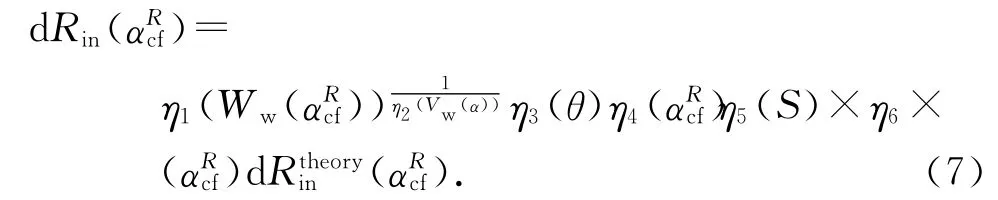
式中:η1(Ww)为水化单元中孔隙中水含量对水泥颗粒内半径变化量的影响系数,η2(Vw)为孔隙饱和度影响系数,η3(θ)为温度对水泥颗粒内半径变化量的影响系数,η4(α)为水化度对水泥颗粒内半径变化量的影响系数,考虑到水泥颗粒的空间分布,η5(S)为水化进程中水化单元水泥颗粒与水的接触面积减小对水泥颗粒半径变化量的折减系数,η6(α)为粉煤灰对水泥水化的延缓效应系数,η1~η6 具体计算可见文献[12].
同理,考虑水分减少、颗粒和水接触面积减少和温度对粉煤灰水化速率的影响,最终粉煤灰颗粒半径变化速率为
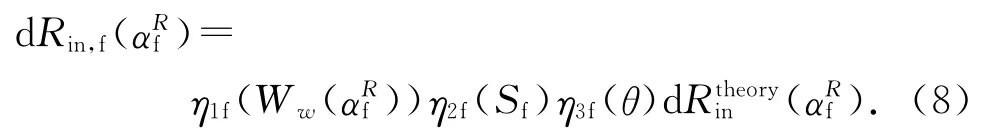
式中:η1f(Ww)为水化单元中水分减少对粉煤灰颗粒内半径变化量的影响系数;η2f(S)为粉煤灰和水接触面积减少对粉煤灰反应的影响;η3f(θ)为温度对粉煤灰颗粒内半径变化量的影响系数.η1f~η3f具体计算可见文献[12].
考虑颗粒粒径分布对水化度的影响,结合粒径分布函数就可以得到水泥及粉煤灰的水化度αi(i=cf,f)和孔隙率φi(i=cf,f):
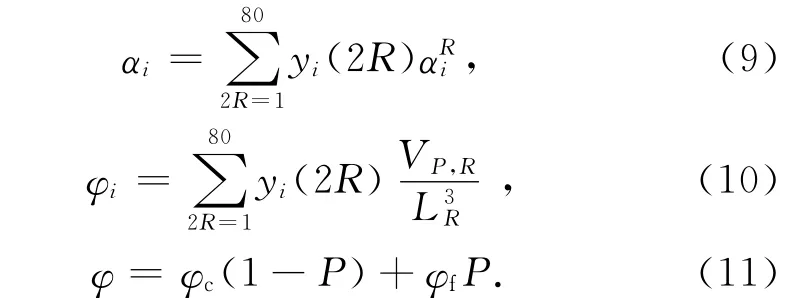
式中:φ 为掺粉煤灰的水泥浆体总孔隙率;P 为粉煤灰掺入比例;y(2R)为粒径分布函数,VP,R为水化单元中水与空气的体积.
2 温湿耦合模型
2.1 温度控制方程
对于非绝热系统,即使外界温度一定,水泥水化进程的放热作用也会使混凝土内部形成不均匀的温度场,本文提出通过水化反应速率把水化微观模型和混凝土温度场联系起来,并且考虑水化过程中温湿度变化对水化速率的影响,因此考虑温湿度场耦合作用的温度控制方程为
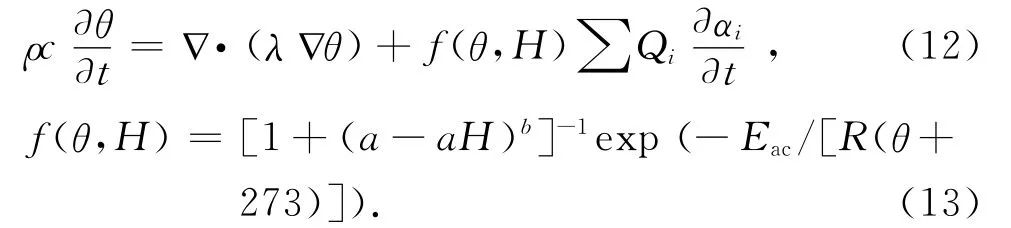
式中:θ 为温度;H 为相对湿度;ρ 为混凝土密度;c为混凝土比热容;λ 为混凝土热传导系数;∂αi/∂t(i=cf,f)为水化反应速率,由上述水化模型得到;f(θ,H)为温度和相对湿度对水化反应速率的影响系数[16];Eac为 水 化 活 化 能;R 为 气 体 常 数;a、b为常数.
Qi(i=cf,f)为单位体积混凝土中水泥或粉煤灰的最大放热量,Qi=miQi∞;mcf、mf分别为单位体积混凝土中水泥、粉煤灰质量;Qf∞为单位质量粉煤灰最大放热量,为 简化起见取常 数[17];Qc∞f为单 位 质量水泥最大放热量,其值取决于水泥中每种组分i的独立放热量Qn及其比例:
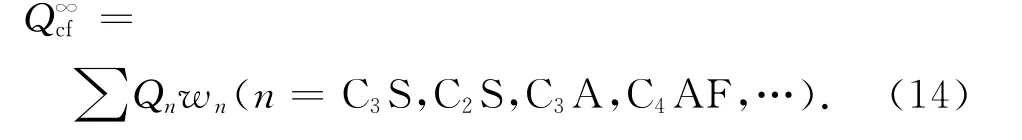
混凝土的热传导系数和混凝土的温度、湿度及龄期相关,为简化计算,忽略粉煤灰水化的影响,其热传导系数与水泥水化度有线性关系[18]:
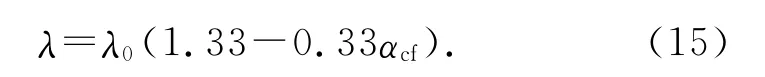
式中:λ0为硬化混凝土的热传导系数.
此外,温度场求解还需要适当的初始及边界条件,在温度边界Γ 上存在热交换时采用Cauchy边界条件:
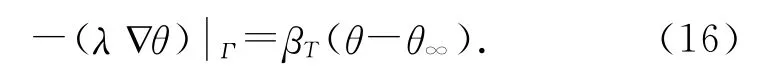
式中:βT 为混凝土表面放热系数,θ∞为外界环境的温度.
2.2 湿度扩散方程
混凝土的相对湿度取决于孔隙气液交界面处弯月面的曲率,混凝土含水量、饱和度、温度等特征都直接和该弯月面的曲率相关[19],因此相对湿度能够反映宏细观之间的联系,且易于测量,本文选择该变量表征混凝土中的湿度特性.
湿度通量正比于孔隙相对湿度,根据传输过程中质量守恒原则,考虑主要的扩散问题而忽略可能存在的对流影响,可得出体积湿含量we与湿度通量Jw的关系[20-21]:

式中:Dh为有关湿度扩散的参数,主要与混凝土孔隙结构、相对湿度和温度相关,呈现非线性;∂we/∂H为混凝土解吸附等温线的斜率,表征混凝土的持水能力.考虑混凝土自干燥作用得出非线性的相对湿度扩散控制方程:
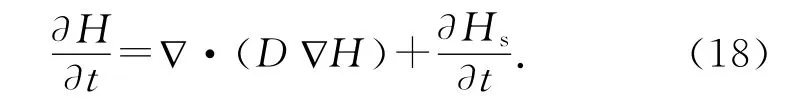
式中:D 为混凝土湿度扩散系数,定义为Dh·∂we/∂H;Hs为只考虑混凝土的自干燥引起的孔隙相对湿度.
自干燥消耗混凝土中的自由水,引起相对湿度的降低,其值同样需要通过解吸附等温线推导[22].在文献[22]的基础上,本文提出采用温湿度对水化速率的影响系数f(θ,H)来考虑温湿度变化对自干燥作用的影响,并以此建立温湿度耦合关系:
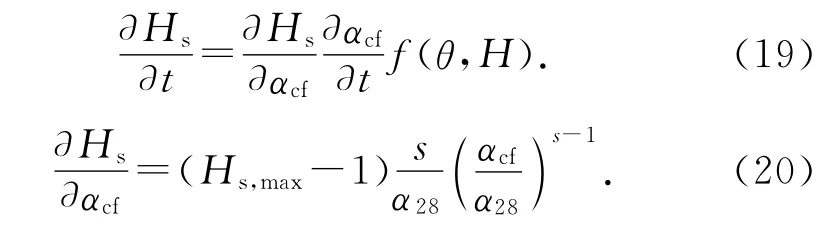
式中:α28为水泥水化28d时的水化度,其值来自上述的微观水化模型;Hs,max为只考虑自干燥情况下水化完成时的相对湿度,由解吸附等温模型逆推得到;s为材料参数,取决于水胶比.与水泥相比,粉煤灰发生化学反应所消耗的水及其在早龄期内的反应程度都远小于水泥[15,23],因此本文忽略所掺入的粉煤灰的自干燥作用.
当混凝土表面与大气接触时,表面的水分会扩散到周围环境中,湿度边界Γ 上的湿度流量一般采用Cauchy边界条件:
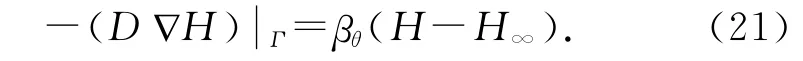
式中:H∞为等效环境相对湿度;βθ 为混凝土表面湿度交换系数,表示水分在空气中的扩散特征,一般通过试验测定,考虑水胶比w/b、温度等因素的影响,这里采用Wong等[24]提出的公式:
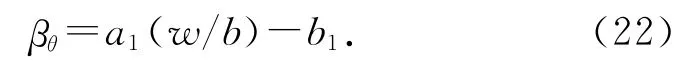
式中:a1、b1为试验参数.
2.3 湿度扩散系数
混凝土的渗透性是由孔隙连通度和孔隙尺寸分布决定的[21],建立准确的预测混凝土渗透性能的模型需要对混凝土随机分布的孔结构尺寸、迂曲度和连通度等特性做恰当的描述和模拟,为简化起见一般采用宏观的湿度扩散系数表示混凝土的渗透性.
Bažant等[21]考虑了相对湿度和温度对湿度扩散系数的关系,但是早龄期微观结构的演化也会影响湿度扩散特性,文献[2]直接考虑龄期对湿度扩散系数进行修正,忽略了不同种类的混凝土的区别;Kang等[25]通过考虑孔隙率的作用来表明水泥水化对湿度扩散系数的影响,水泥颗粒在水化单元中增长到一定程度时,相邻颗粒会相互接触,接触的面积越大,孔隙率越低,这种孔隙结构的变化是造成混凝土扩散性能改变的重要原因.因此,考虑孔隙率影响的湿度扩散系数为
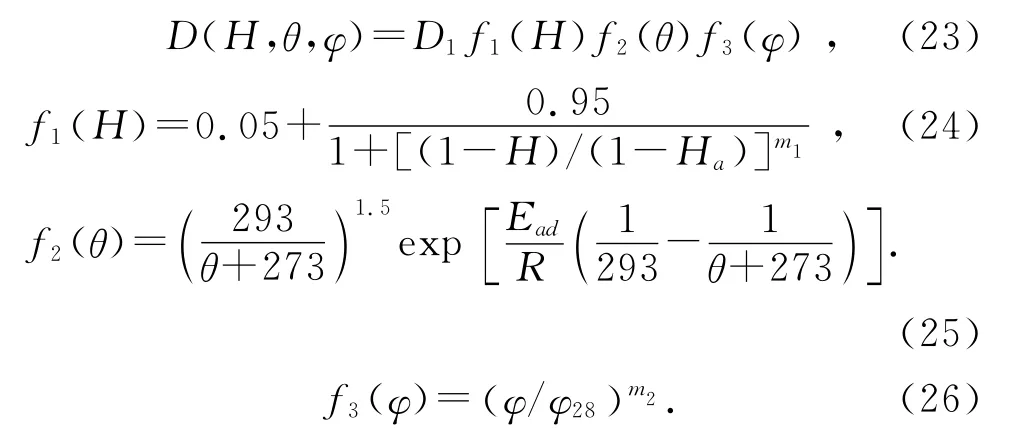
式中:D1为混凝土饱和情况下的参考扩散系数(θ=20 ℃);Ha、m1、m2为常数;Ead为扩散活化能;φ28是混凝土28d时的孔隙率.结合微观水化模型的温湿扩散模型计算流程图如图2所示.
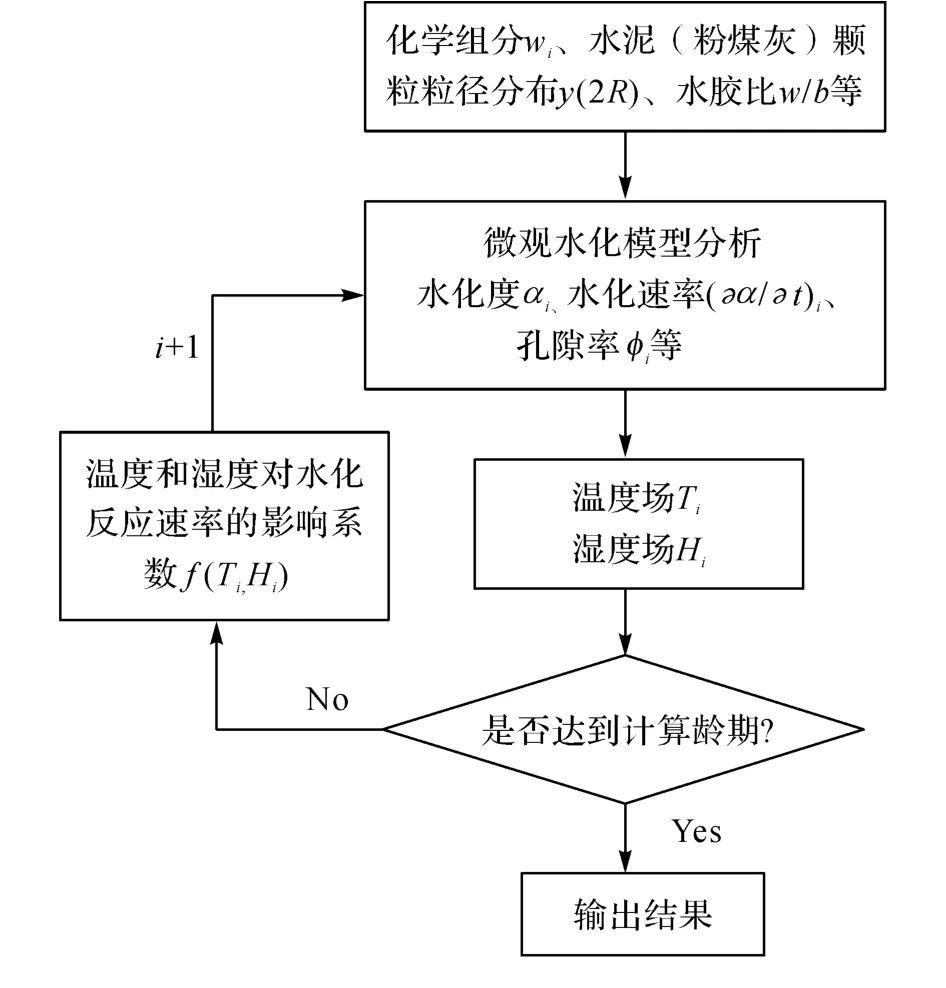
图2 模型计算流程图Fig.2 Flow chart of calculation of model
3 数值模拟及验证
3.1 试验概况
采用混凝土梁试验[18,26-27]验证本研究建立的混凝土温湿度耦合作用模型.试验采用的混凝土梁的尺寸为200mm×200mm×800mm,浇筑时在模具内表面衬上一层塑料膜,并在模具外围和底部用泡沫板隔热隔湿,只留出上浇筑面与空气接触,采用套有PVC塑料管的JWSL-5ATD 型温湿度传感器采集数据,PVC管上端通过高分子密封胶密封,下端(即测点处)开有缝隙以便传感器与测点的温湿交换与平衡.取试件中分散开来的3个测点,即距离上表面25、100、180mm 处3个测点进行验证,试件及测点位置如图3所示.水泥矿物组分、混凝土配合比分别如表1、2所示.混凝土水化进程及温湿传输模拟所需要的材料参数如表3、4所示.
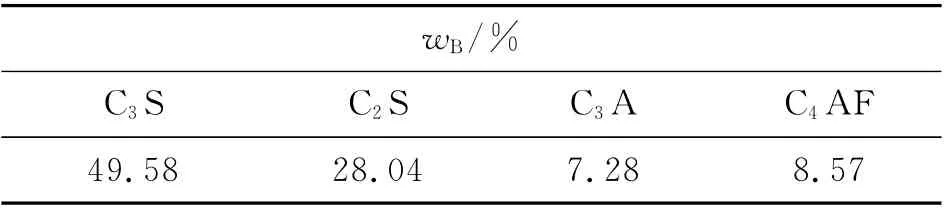
表1 实测水泥矿物组分[18]Tab.1 Measured mineral composition of cement[18]
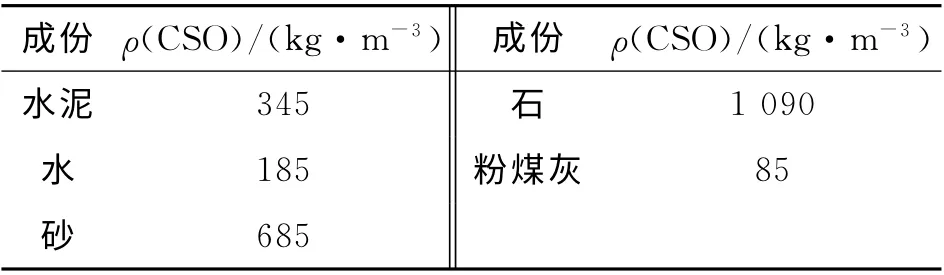
表2 混凝土配合比[18]Tab.2 Concrete mixes[18]

表3 水化动力学反应常数[12]Tab.3 Hydration kinetics parameters[12]

表4 混凝土温湿传输模拟参数Tab.4 Parameters for hygro-thermal simulations

图3 试件及测点位置Fig.3 Specimen and position for measurement
3.2 参数验证
准确地描述水化进程的水化模型是预测混凝土温湿扩散的基础,本文改进的微观水化模型只需要原材料的信息(化学组分、水泥(粉煤灰)颗粒粒径分布、水胶比等)即可预测水化进程.微观水化模型计算值和由绝热温升试验得到的水化度试验值对比如图4所示.可见在不同水胶比的情况下,模型计算值与试验值吻合良好.在水化早期总体上水化模型计算值要稍大于试验值,水胶比w/b 为0.62时误差相对较大,最大误差达到10.6%,这是因为水化模型中含水量对水泥颗粒半径变化量参数比较敏感,当含水量较大时水化速率较快,求解误差变大,在水化后期(7d后)对不同水胶比的混凝土水化度的误差能控制在4%以内,说明本文提出的微观水化模型是较为准确的.文献[18]通过干湿对比试验求解出的混凝土湿度扩散系数与本文的数值模拟值对比如图5所示.可以看出相对湿度对湿度扩散系数有很大的影响,当相对湿度在90%以下时,湿度扩散系数基本不变,而当相对湿度大于90%时,湿度扩散系数迅速增大,这说明混凝土在高湿状态下(液态水为主)的扩散性能显著,也可以看出液态水的扩散作用要大于气态水的扩散作用,此时液态水的扩散作用占主导作用,当相对湿度降低,气态水的扩散作用逐步占据主导作用.图中模拟值和试验值非常接近,当相对湿度为100%时,模拟值是试验值的1.7倍,但这种状态一般出现在水化初期,维持时间较短,对温湿度扩散作用的影响有限.
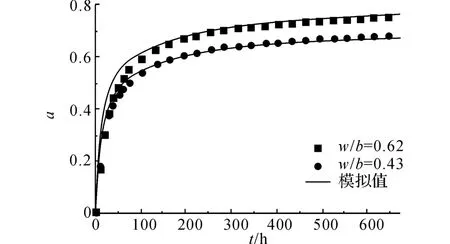
图4 水化度模拟值和试验值对比Fig.4 Comparison of calculated and measured hydration degree
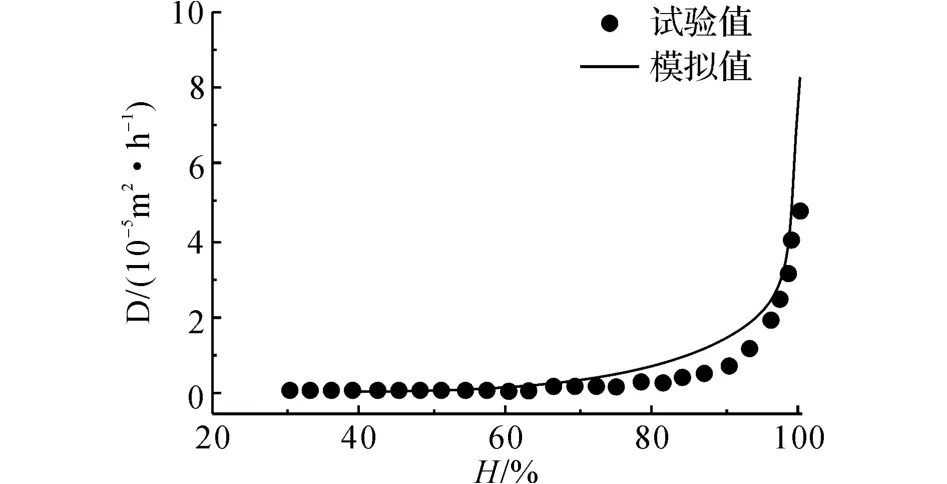
图5 C50混凝土湿度扩散系数模拟值和试验值对比Fig.5 Comparison of calculated and measured moisture diffusion coefficient of C50concrete
3.3 温湿耦合分析
本文采用Matlab软件实现水化模型的数值计算,采用多物理场耦合软件COMSOL Multiphysics求解温湿耦合模型中非线性的偏微分方程组(PDEs),并实现二者的交互计算.该试验设计在理论上可以假设成温湿度场的一维传输,但为准确性考虑,数值模拟时将其简化成横断面上的二维传输问题,取对应测点的模拟值与试验值进行比较研究.
各测点7d内的温度变化如图6(a)所示,由试验及模拟结果可以看出,由于浇筑初期的水化放热作用,温度在短期内迅速上升并形成温度梯度,且在12~24h达到峰值,在第3d时温度梯度作用基本消除.模拟值与试验值在180和100 mm 处吻合较好,但是在25mm 处的温度峰值附近模拟值要稍高于试验值(最大相差1.8 ℃),这主要是因为该测点的位置十分接近混凝土表面,加上传感器探头有一定的尺寸,要准确测量该测点的温度难度较大.总体来说,上述考虑水化放热的热传导方程可以较好地描述混凝土早龄期的温度变化过程.
各测点28d内的相对湿度模拟值和试验值如图6(b)所示,可以看出由水泥水化和水分蒸发导致的各测点相对湿度的降低.180 mm 处的模拟值与试验值吻合较好,但是在混凝土水化前期(0~7d),25和100mm 处相对湿度的模拟值和试验值相差较大,且距离边界越近相差越大,试验值基本处在100%,模拟值从初始时刻起就有明显的下降过程.这是因为试验中采用的电容式温湿度传感器在高湿状态(H>90%)下不够灵敏(误差±3%),因此这一时期的湿度测量不够精准.但是这种影响会随着龄期的增加、湿度的降低逐渐减弱,7d以后相对湿度基本上小于90%,模拟值和试验值吻合良好.
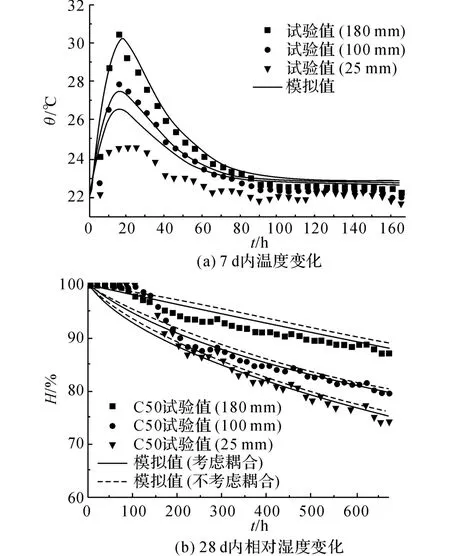
图6 混凝土温湿度模拟值和试验值对比Fig.6 Comparison of calculated and measured of temperature and humidity of concrete
模型中温湿耦合作用主要是通过温度和相对湿度对水化反应速率的影响系数f(θ,H)和湿度扩散系数D(H,θ,φ)来体现的,分析表明本试验中早龄期混凝土温湿耦合作用并不显著,如图6(b)所示.不考虑耦合作用,即不考虑温度场对湿度场的影响时,各测点相对湿度的下降速度要相对变慢,且到后期差距趋于平稳.本试验中水化初期(0~3 d)温度升高使湿度扩散系数增大,同时会使水化速率加快,但温度作用时间短,当温度平稳后其对湿度扩散系数及水化速率的影响有限,而且试件尺寸较小,所以温度作用不显著.因此从整体上看在水化初期温度对相对湿度的降低有一定影响,在水化后期相对湿度的降低是由湿度控制的,温度作用可以忽略.但是温湿耦合分析仍能从理论上对大体积混凝土及复杂外部环境下的混凝土温湿关系的研究提供支持.
4 结 论
(1)改进的微观水化模型可根据有关水泥(粉煤灰)的原材料信息预测水化进程,对不同水胶比的混凝土能够较准确地预测其水化度变化情况;
(2)基于改进的微观水化模型得出的水化度、水化速率等参数建立起了混凝土宏观温湿耦合扩散与微结构演化的联系,能够较为准确地预测早龄期混凝土的温湿度分布情况;
(3)对于小体积的早龄期混凝土而言,温湿耦合作用并不明显,在水化初期温度对湿度的扩散有一定影响,但在水化后期湿度梯度控制着湿度的扩散,温度作用可以忽略.
(
):
[1]SONG H W,KWON S J.Permeability characteristics of carbonated concrete considering capillary pore structure[J].Cement and Concrete Research,2007,376:909-915.
[2]HAN S H.Influence of diffusion coefficient on chloride ion penetration of concrete structure[J].Construction and Building Materials,2007,212:370-378.
[3]SMILAUER V,KREJCI T.Multiscale model for tempe-rature distribution in hydrating concrete[J].International Journal for Multiscale Computational Engineering,2009,72:135-151.
[4]MAEKAWA K,ISHIDA T,KISHI T.Multi-scale modeling of concrete performance[J].Journal of Advanced Concrete Technology,2003(12):91-126.
[5]KLEMCZAK B.Prediction of coupled heat and moisture transfer in early-age massive concrete structures[J].Numerical Heat Transfer Part A:Applications,2011,60(3):212-233.
[6]CERVERA M,OLIVER J,PRATO T.Thermochemo-mechanical model for concrete.I:Hydration and aging[J].Journal of Engineering Mechanics,1999(1259):1018-1027.
[7]GAWIN D,PESAVENTO F,SCHREFLER B A.Hygro-thermo-chemo-mechanical modeling of concrete at early ages and beyond.Part I:hydration and hygrothermal phenomena[J].International Journal for Numerical Methods in Engineering,2006(673):299-331.
[8]TIAN Y,JIN X Y,JIN N G.Thermal cracking analysis of concrete with cement hydration model and equivalent age method[J].Computers and Concrete,2013(114):271-289.
[9]PARK K B,TAKAFUMI N,PLAWSKY J.Modeling of hydration reactions using neural networks to predict the average properties of cement pastes[J].Cement and Concrete Research,2005,35(9):1676-1684.
[10]田野.复掺矿物掺合料混凝土性能及抗裂机理、微观特性研究[D].杭州:浙江大学,2007.TIAN Ye.Investigation on the performance,cracking mechanism and micro-properties of concrete incorporated with mineral admixtures[D].Hangzhou:Zhejiang University,2007.
[11]BENTZ D P,GABOCZI E J.Percolation of phases in a three-dimensional cement paste microstructural model[J].Cement and Concrete Research,1991,21:325-344.
[12]王宇纬.掺矿物掺合料水泥水化模型及其应用研究[D].杭州:浙江大学,2014.WANG Yu-wei.Study of hydration model of cement with mineral admixtures and its application[D].Hangzhou:Zhejiang University,2014.
[13]DABI P,KRSTULOVI R.A new approach in mathematical modeling of cement hydration development[J].Cement and Concrete Research,2000,30:1017-1021.
[14]WANG X Y,LEE H S,PARK K B.Simulation of low-calcium fly ash blended cement hydration[J].ACI Material Jounal,2009(1062):167-175.
[15]ZENG Q,LI K F,FEN C T,et al.Determination of cement hydration and pozzolanic reaction extents for fly-ash cement pastes[J].Construction and Building Materials,2012(271):560-569.
[16]DI LUZIO G,CUSATIS G.Hygro-thermo-chemical mod-eling of high performance concrete.I:Theory[J].Cement and Concrete Composites,2009(315):301-308.
[17]SCHINDLER A K,FOLLIARD K J.Heat of hydration models for cementitious materials[J].ACI Materials Journal,2005(1021):24-33.
[18]侯东伟.混凝土自身与干燥收缩一体化及相关问题研究[D].北京:清华大学,2010.HOU Dong-wei.Integrative studies on autogenous and drying shrinkage of concrete and related issues[D].Beijing:Tsinghua University,2010.
[19]GRASLEY Z C,LANG D A,D’AMBROSIA M D,et al.Relative humidity in concrete[J].Concrete international,2006,28(10):51-57.
[20]BAANT Z P,NAJJAR L J.Nonlinear water diffusion in nonsaturated concrete[J].Matériaux et Construction,1972(51):3-20.
[21]BAANT Z P,THONGUTHAI W.Pore pressure and drying of concrete at high temperature[J].Journal of Engineering Mechanics Division,ASCE,(104EM5):1978,1095-1079.
[22]OH B H,CHA S W.Nonlinear analysis of temperature and moisture distributions in early-age concrete structures based on degree of hydration[J].ACI Materials Journal,2003(1005):361-370.
[23]HANEHARA S, TOMOSAWA F, KOBAYAKAWAA M,et al.Effects of water/powder ratio,mixing ratio of fly ash,and curing temperature on pozzolanic reaction of fly ash in cement paste[J].Cement and Concrete Research,2001(311):31-39.
[24]WONG S F,WEE T H,SWADDIWUDHIPONG S,et al.Study of water movement in concrete[J].Magazine of Concrete Research,2001(533):205-220.
[25]KANG S T,KIM J S,LEE Y,et al.Moisture diffusivity of early age concrete considering temperature and porosity[J].KSCE Journal of Civil Engineering,2012(161):179-188.
[26]ZHANG J,HOU D W,HAN Y D.Micromechanical modeling on autogenous and drying shrinkages of concrete[J].Construction and Building Materials,2012(293):230-240.
[27]ZHANG J,HOU D W,GAO Y,et al.Determination of moisture diffusion coefficient of concrete at early-age from interior humidity measurements[J].Drying Technology,2011(296):689-696.
