基于OELM 重构极限状态函数的可靠度计算方法
2015-08-10赖雄鸣
赖雄鸣,张 勇,王 成,言 兰,缑 锦
(1.华侨大学 机电及自动化学院,福建 厦门361021;2.华侨大学 计算机科学与技术学院,福建 厦门361021)
在工程可靠性问题中,极限状态函数往往不解析、非线性.每一次极限状态函数评估需要通过有限元方法进行大规模数值求解[1].在可靠性问题的求解中,循环计算极限状态函数需要更大规模的计算量,有时往往难以接受.
常规可靠性计算方法可以分为2类[2].1)基于Monte Carlo抽样的计算方法及改进算法(如重要抽样法[3]、子集抽样法[4]、线抽样法[5]等).该类方法计算简单,适用性强,精度高,但是由于计算过程中样本的选取具有随机性,需要大规模重复计算极限状态函数,总体效率较低,难以接受.2)基于梯度的计算方法[6].该方法以计算MPP 点为中心,如国际安全度联合委员会(JCSS)推荐使用的JC 法.该方法存在迂回振荡、甚至不收敛的情况发生.Lee等[7-12]提出各种改进迭代方法,确保收敛性,从而克服了JC法的缺点.虽然上述改进算法对于非线性极限状态函数有较强的适应性(即较快收敛到MPP点),但是本质上属于一次二阶矩法,仍然是在MPP点附近以一次超平面代替非线性极限状态曲面,存在计算误差大,甚至错误的情况发生.尽管二次二阶矩法较一次二阶矩法,精度有所提高,但是当极限状态函数的非线性较强时,与第一类方法相比,误差较大.
对于极限状态函数的非线性、不解析,且需要大量数值计算等特征,第一类方法计算效率低,第二类方法计算精度不足.针对该问题,本文提出基于极限学习机高效循环重构极限状态函数的可靠度计算方法.该方法首先确定可靠度的重要影响区域,然后在该区域内按照一定的策略,有目的性地选择计算样本,进行高效循环重构极限状态函数,以期最大限度地减少极限状态函数计算次数.最后,在该重构的近似极限状态函数模型的基础上利用重要抽样方法,快速进行模拟计算可靠度,最终实现较少次数的计算极限状态函数,能够获得高精度可靠度计算结果.
1 基于优化的极限学习机(OELM)
对于给定N 个不同的训练数据集{xi,yi|i=1,…,N},其中xi=[xi1,xi2,…,xin]∈Rn,yi∈RL.具有L 个隐节点,激活函数为K(xi)的标准单隐层前馈网络(SLFN)可以零误差地逼近任意的N个样本,表示为[13]
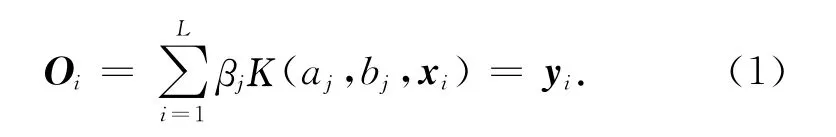
式 中:aj为 输 入 权 值,bj为 隐 层 节 点 的 阈 值,xi为 输入向量,Oi为输出向量,βj 为输出权值.激活函数K可以取sigmoid、rbf、hardlim[14].这里取常用的rbf.
式(1)可以简写为

式中:β=[β1,β2,…,βL]T,Y=[y1,y2,…,yN]T;H 为隐层输出矩阵,
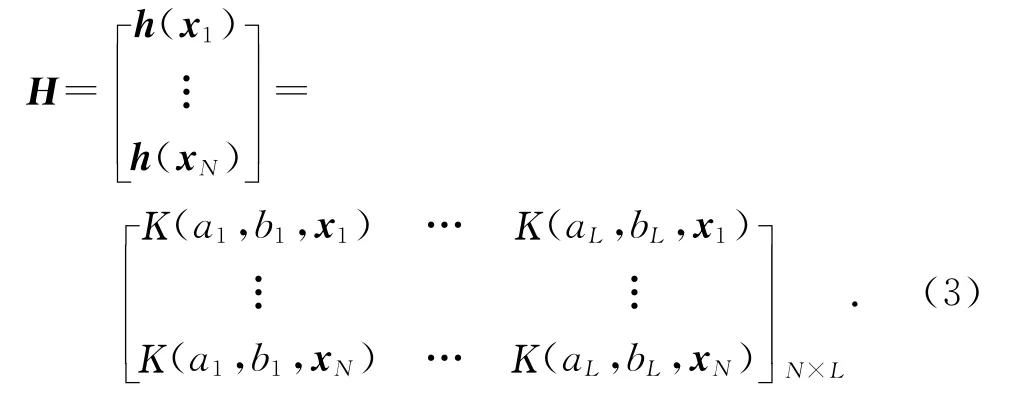
ELM 学习算法的优化目标是同时最小化训练误差和输出权重的范数,由此可得

为了提高模型的泛化能力,Huang等[13]通过基于优化的方法统一了ELM 和SVM,并提出改进OELM,即

常数C 可以取较大的数,这里取1012.最后输出函数为

2 基于OELM 高效重构极限状态函数的可靠度计算方法
该方法的主要求解思路如下:1)快速确定对可靠度影响的重要区域位置;2)划定重要区域范围;3)在该重要区域内,有目的性的选择计算样本,并高效循环重构高阶极限状态函数;4)基于重构极限状态函数,进行重要抽样模拟计算;5)重复步骤2)和3),直到判断计算收敛为止.
2.1 可靠度影响重要区域位置快速确定
对于包含任意随机变量的可靠性问题,总可以通过Rosenblatt变换[15]将非正态变量变换为标准正态随机变量.假定极限状态函数中的随机变量均服从标准正态分布.为了快速确定可靠度影响的重要区域,提出基于梯度步长的搜索算法,具体步骤如下.
1)设置标准正态空间内前进步长L=0.2~1.5.
2)从标准正态空间的原点开始,沿着原点位置处极限状态函数的负梯度方向(▽G(0))前进L 距离到达新的点P1.若判断P1点处于失效区域,则停止;否则,执行步骤3).
3)沿着P1点处极限状态函数的负梯度方向前进L 距离到达Pi点.若Pi点处于失效区域,则停止.否则重复执行步骤3),直到新点处于失效域.
4)假设前进m 次,最后的位置点为Pm,以该点表示可靠度影响重要区域的大致位置.
结合文献[11]的算例来说明这一方法.如图1所示,结构功能函数为
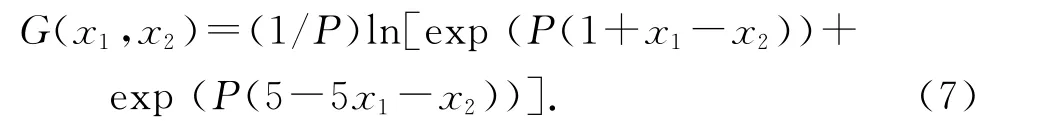
式中:P=1;x1、x2为相互独立的标准正态分布随机变量.图1中,箭头方向表示该极限状态函数曲线簇G(x1,x2)=C 在不同位置的梯度方向.可以看出,该极限状态函数簇的非线性很强,梯度从左到右变化很大.此处取步长L=0.5.图1中,前进了7次,走到失效区域中的P7点.该位置点可以表示可靠度影响重要区域的大致位置.
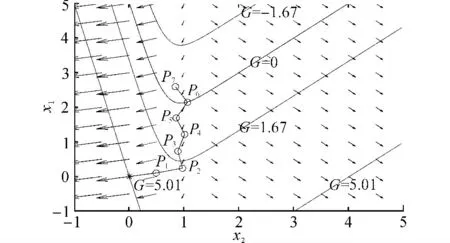
图1 可靠度影响重要区域位置确定快速方法Fig.1 Fast method for determining position of important area for reliability
由于只要大致确定可靠度影响的重要区域位置,P7点的位置不必很精确,N 可以取更小,即通过前进增加步长,减少前进到失效区域中所需的次数,进而减少极限状态函数的计算次数.在后文实例中将给出进一步说明.
对于极限状态函数不解析的情形,可以采用差分方法,近似获得其梯度,如下式所示:
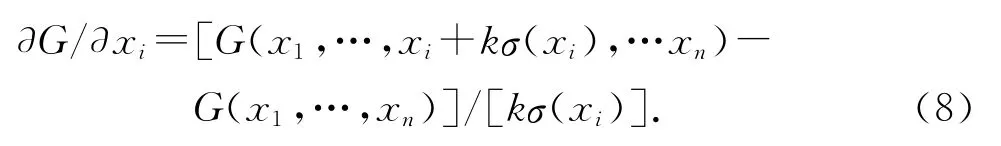
式中:σ(xi)为标准正态随机变量xi的标准差,为1.通常系数k越小,梯度近似越准确,本文k取0.001.
2.2 可靠度影响重要区域划定
以二维随机变量情形进行介绍.图2中,Pm为2.1 节方法中所求得的点.假设点Pm的坐标为(xp1,xp2),可以获得点Pm附近的其他点M1~M4,坐标分别为(xp1-k′σx1,xp2)、(xp1,xp2-k′σx2)、(xp1+k′σx1,xp2)、(xp1,xp2+k′σx2).这里系数k′可取0.5.分别建立原点与点Pm、M1~M5的直线l0~l5.通过插值法可以求得上述直线与极限状态函数的交点Q0~Q4,即为极限状态曲面重要区域上的失效点.以求Q1点为例,给出快速插值求解算法.
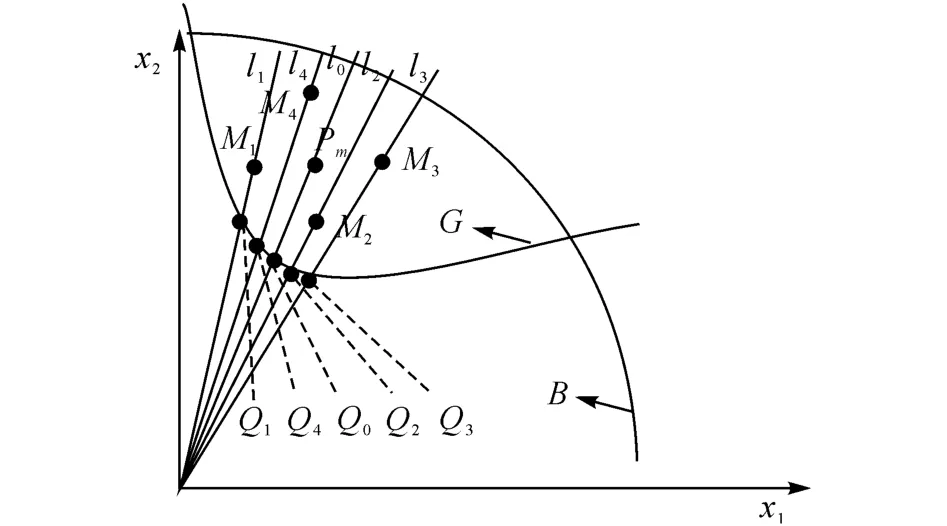
图2 二维随机变量情形下获取极限状态曲面重要区域上的初始失效点Fig.2 Obtaining initial failure points on limit state function for two dimensional case
1)令t=0对应直线l1上的原点,t=1 对应直线l1上的点M1.
2)令T=[0,1],Y=[G(x=0),G(x=xM1)],则通过分段三次埃尔米特插值法可以得到G=0时,对应的tnew.
3)由此获得tnew对应直线l1上的点xnew=0+tnew(xM1-0).
4)评估xnew位置处的极限状态函数值G(x=xnew).若|G(x=xnew)|<ε1(取10-3),则停止计算;否则令T=[T(2),tnew],Y=[Y(2),G(x=xnew)],通过分段三次埃尔米特插值法获得tnew,然后重复步骤3).
在获取到上述极限状态曲面重要区域上的初始失效点后,将失效点Q0~Q4以及点Pm、M1~M4组合在一起,可得坐标点集X 及对应的初始极限状态函数响应集Y.基于OELM,建立X→Y 的映射,可以构建初始极限状态函数,设为.利用式(9),可得对应的初始MPP点.
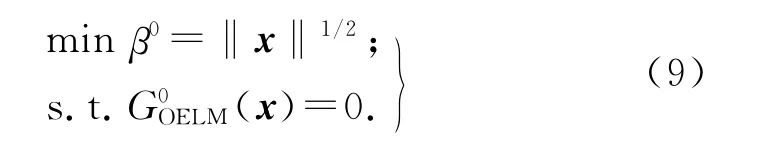

图3 可靠度影响重要区域划定Fig.3 Outlining important area for reliability
2.3 基于OELM 循环重构重要区域内极限状态函数
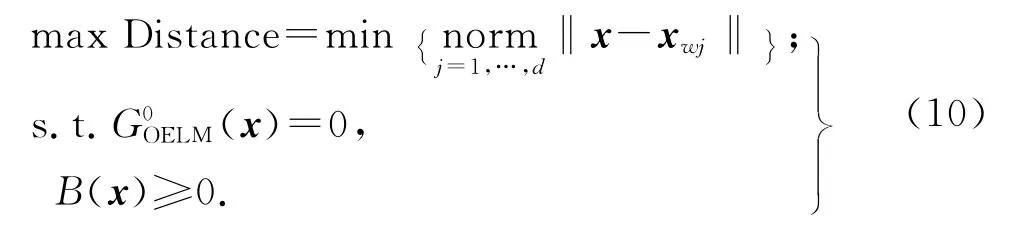
式中:xwj为重要区域内(x)曲面上已经找到的点(见图4中的点W1,W2,…,Wd).式(5)表示在重要区域内的(x)曲面上寻找最稀疏区域的位置点.
在求解式(10)的过程中,采用常规优化算法或智能集群算法不一定总找到全局最优解,难免陷入局部解.建议在给定初始解x0时,分别令x0=xwj(j=1,…,d),由此可得不同的局部解,然后选择最距离最大(即式(10)中计算的Distance值最大)的局部解作为该型样本点.于是,可以取得相对较好的结果.
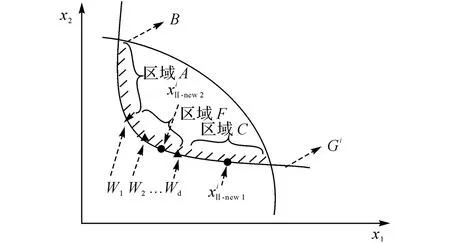
图4 可靠度影响重要区域Ⅱ型点的寻找Fig.4 Searching Ⅱ-type point in important area for reliability
1)首先在点W1,W2,…,Wd群中,挑选出最外围的点组成集合X′.属于X′中的每个点具有如下特性,存在沿着某一维的坐标中,其坐标值是W1,W2,…,Wd中的最大或最小值.如图4所示的二维情形,W1和Wd为点W1,W2,…,Wd群中的最外围点.
2)分别选取集合X′的每个点作为初值x0,然后按照式(11)寻找距离原点更远的点,最后选取最远的点作为Ⅲ型样本点.如图5所示,x0分别选取W1和Wd作为初始点,然后代入求解式(11),可以求得各自对应的最外围点,分别是P1和P2.进一步地,由于OP1>OP2,选择点P1作为Ⅲ型样本点.
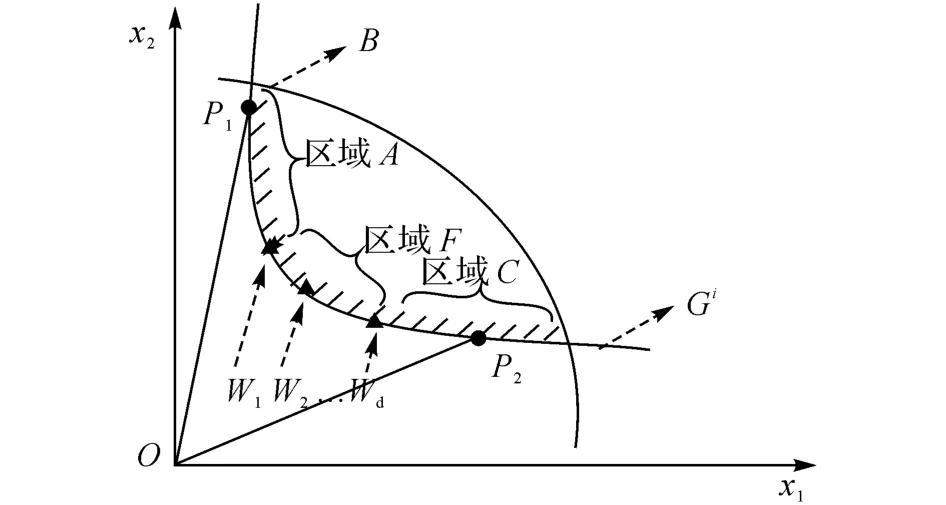
图5 可靠度影响重要区域Ⅲ型点x的寻找Fig.5 Searching Ⅲ-type point in important area for reliability
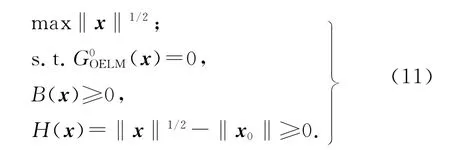
2.3.4 重要区域内极限状态函数重构 在重构限状态曲面的基础上,将上述寻找到的I~Ⅲ型样本点作为新的样本点,计算对应的真实极限状态响应,并加入坐标点集X 和极限状态函数响应集Y.然后基于OELM 方法重构X→Y 的映射,可以获得重要区域内逼近精度更高的极限状态函数.重复上述过程,随着重构次数i的增加,可以最大限度地提高重要区域内的极限状态函数逼近精度.
3 计算实例
本文的计算方法特别适用于极限状态函数为非线性、不解析,且需要花费大规模数值求解的情形.下面的计算实例中,其极限状态函数均为已知的情形,以便比较本方法计算值和理论值的差别,从而验证该方法的有效性.在应用本文方法计算下面的实例时,其极限状态函数当作未知来处理(如采用差分方式计算梯度).通过与不同计算方法作比较,验证本文提出的方法只要较少次数计算极限状态函数就可获得高精度的计算结果.
实例一:某结构指数形式的极限状态函数[10-11,15]为
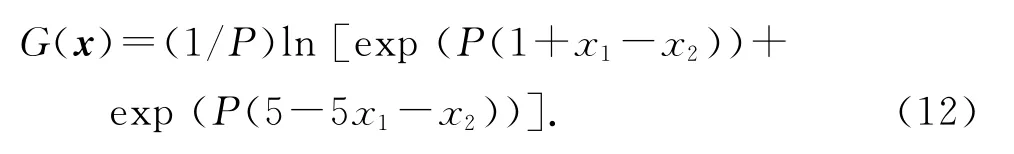
式中:x1~N(0,1),x2~N(0,1);参数P=1.
该极限状态函数的非线性强,采用JC 法计算不收敛.表1 中,周凌等[10-11,16]分别通过14、10、17次迭代,找到MPP点,并计算可靠性指标为2.999 5.对于这类非线性问题,计算可靠性指标无太大意义,因为由该可靠性指标计算的失效概率为0.001 35,而表2中蒙特卡洛法的计算结果为0.002 984,两者相差很大.
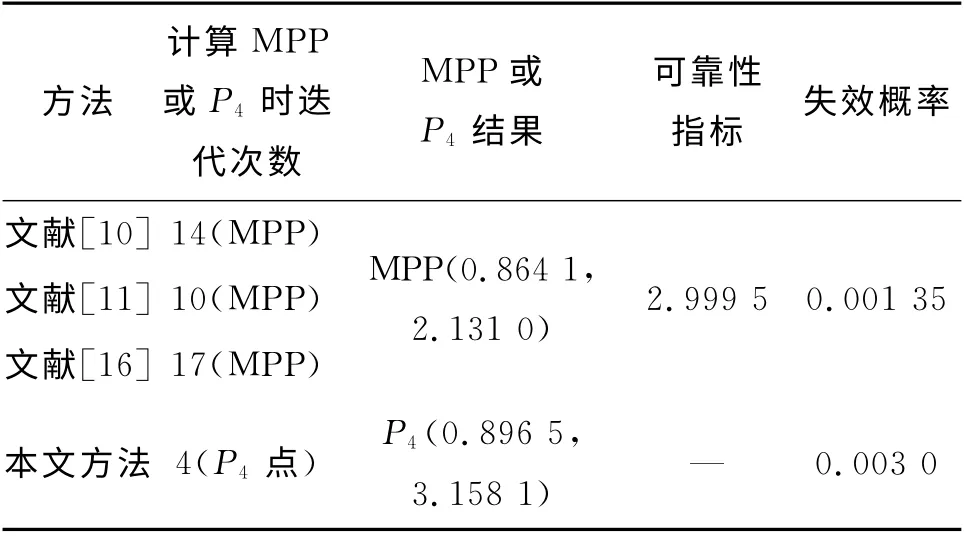
表1 实例一可靠度计算结果比较Tab.1 Comparison of computed results in example 1
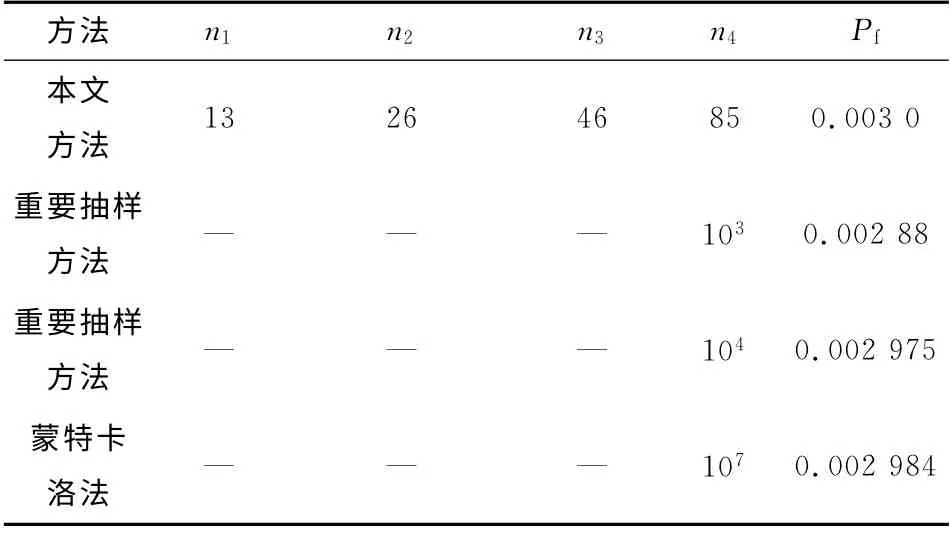
表2 实例一不同计算方法效率评估Tab.2 Comparison of computational efficiency between different methods in example 1
对于复杂非线性问题,在计算MPP 和可靠性指标时,迭代次数有时过多,计算量过大,而计算误差也大.因此,没有必要消耗太多计算量计算MPP和可靠性指标.按照本文方法,通过少量迭代次数,快速确定重要区域的大致位置.如图6所示,取步长L=1,经过4次迭代可以快速确定重要区域的大致位置在P4点.然后按照2.2、2.3节介绍的方法,如图7所示为经过21次重构,可以获得可靠度计算结果,收敛值为0.003 0.
表2中除了采用本文方法和蒙特卡洛法外,还采用重要抽样方法计算该实例.该重要抽样方法采

图6 实例一可靠度重要影响区域快速确定Fig.6 Fast method for determining position of important area for reliability in example 1
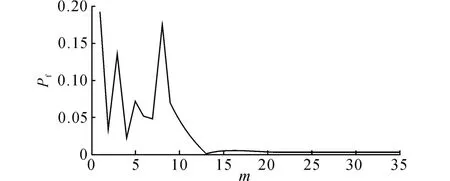
图7 实例一极限状态函数不同重构次数对应的可靠度计算结果Fig.7 Reliability results corresponding to different number of reconstruction of limit state function in example 1
用表一中的MPP点作为抽样中心,分别按照1 000次和10 000次抽样规模计算,结果示于表2.表中,n1为计算P3时极限状态函数计算次数,n2为计算M1~M4、Q0~Q5时极限状态函数计算次数,n3为极限状态函数重构时极限状态函数计算次数,n4为极限状态函数总计算次数.可以看出,本文的计算方法相当高效,第21次重构后,共进行85次极限状态函数计算即可获得精确的计算结果.
实例二:已知极限状态函数[11]为

式中:x1~N(10,5),x2~N(9.9,5).
该极限状态函数的非线性较强,采用JC 法计算不收敛.表3 中,杨杰等[11]通过5 次迭代,得到MPP点,对应的可靠性指标为2.298 3,失效概率为0.010 8.表4中,蒙特卡洛法的计算结果为0.005 875,两者相差很大.本文步长取1,如图8所示,经过3次迭代得到P3点.在此基础上,如图9所示,经过14次重构后,可以获得可靠度计算结果,收敛值为0.005 7.
表4中的重要抽样方法以杨杰等[11]计算的MPP点为抽样中心,分别进行1 000和10 000次抽样计算.通过比较3种方法的计算结果,可以验证本文方法计算高效,计算结果准确.
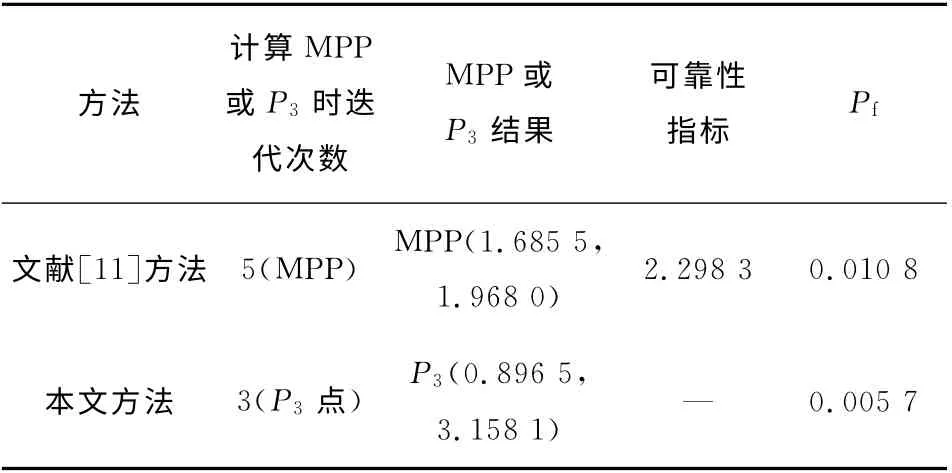
表3 实例二计算结果比较Tab.3 Comparison of computed results in example 2

表4 不同计算方法效率评估Tab.4 Comparison of computational efficiency between different methods in example 1

图8 实例二可靠度重要影响区域快速确定Fig.8 Fast method for determining position of important area for reliability in example 2

图9 实例二极限状态函数不同重构次数对应的可靠度计算结果Fig.9 Reliability results corresponding to different number of reconstruction of limit state function in example 2
4 结 语
针对工程可靠性计算中,极限状态函数不解析、非线性、计算量大的问题,本文提出高效、高精度的可靠度计算方法.该方法首先基于梯度步长搜索算法快速确定可靠度影响重要区域,然后按照一定策略有目的性地选择计算样本,基于OELM 方法高效重构极限状态函数.在此基础上,利用重要抽样方法,快速进行模拟可靠度计算.采用该方法可以有效地减少极限状态函数计算次数,同时可以获得高精度可靠度的计算结果,对实际工程的可靠性计算具有重要意义.
(
):
[1]张惠峰,关富玲,侯国勇.考虑扭簧失效的桁架式可展开天线可靠性研究[J].浙江大学学报:工学版,2010,44(6):1207-1212.ZHANG Hui-feng,GUAN Fu-ling,HOU Guo-yong.Reliability analysis of truss deployable antenna considering torsional spring failure[J].Journal of Zhejiang University:Engineering Science,2010,44(6):1207-1212.
[2]CHOWDHURY R,RAO R B.Hybrid high dimensional model representation for reliability analysis[J].Computer Methods in Applied Mechanics and Engineering,2009,198(5/6/7/8):753-765.
[3]LAI X M,DUAN J A.Probabilistic approach to mechanism reliability with multi-influencing factors[J].Proceedings of the Institution of Mechanical Engineers,Part C,Journal of Mechanical Engineering Science,2011,225(C12):2991-2996.
[4]陈向前,董聪,闫阳.结构可靠性分析的自适应子集模拟方法[J].计算力学学报,2013,30(5):627-632.CHEN Xiang-qian,DONG Cong,YAN Yang.Structural reliability failure probability subset Simulatiom adaptive optimal sample size[J].Chinese Journal of Computational Mechanics,2013,30(5):627-632.
[5]何红妮,吕震宙.正态变量相关情况下可靠性灵敏度分析的新方法[J].计算力学学报,2011,28(3):436-443.HE Hong-ni,LV Zhen-zhou.Correlative variable independent variable reliability sensitivity dependence variation coefficient[J].Chinese Journal of Computational Mechanics,2011,28(3):436-443.
[6]张凯,李刚.基于改进降维法的可靠度分析[J].计算力学学报,2011,28(2):187-192.ZHANG Kai,LI Gang.Reliability analysis based on the improved dimension reduction method [J].Chinese Journal of Computational Mechanics,2011,28(2):187-192.
[7]LEE J K,YANG Y S,RUY W S.A comparative study on reliability-index and target-performance-based probabilistic structural design optimization [J].Computers and Structure,2002,80(3/4):257-269.
[8]SANTOSH T V,SARAF R K,GHOSH A K.Opti-mum step length selection rule in modified HL-RF method for structural reliability[J].International Journal of Pressure Vessels and Piping,2006,83(10):742-774.
[9]贡金鑫.结构可靠性指标求解的一种新的迭代方法[J].计算结构力学及其应用,1995,12(3):369-373.GONG Jin-xin.A new algorithm for solving the structural reliability index[J].Computational Structural Mechanics and Applications,1995,12(3):369-373.
[10]周凌,贾宏光,安伟光.相关正态空间中改进的有限步长迭代法[J].工程力学,2012,29(11):137-142.ZHOU Ling,JIA Hong-guang,AN Wei-guang.Modified limit step length iteration algorithm in correlation normal space [J]. Engeering Mechanics,2012,29(11):137-142.
[11]杨杰,赵德有.结构可靠性指标计算的旋转梯度算法[J].大连理工大学学报,2011,51(2):221-225.YANG Jie,ZHAO De-you.Rotation gradient algorithm for calculating structural reliability index [J].Journal of Dalian University of Technology,2011,51(2):221-225.
[12]蒋友宝,冯健,孟少平.求解结构可靠性指标的线性可行方向算法[J].东南大学学报:自然科学版,2006,36(2):312-315.JIANG You-bao,FENG Jian,MENG Shao-ping.Linear feasible direction algorithm for calculation of reliability index of structure[J].Journal of Southeast University:Natural Science Edition,2006,36 (2):312-315.
[13]HUANG G B,WANG D H,LAN Y.Extreme learning machines:a survey[J].International Journal of Machine Leaning and Cybernetics,2011,2(2):107-122.
[14]史峰,王辉,郁磊,等.智能算法[M].北京:北京航空航天大学出版社,2011.
[15]ROSENBLATT M.Remarks on a multivariate transformation [J].Annals of Mathematical Statistics,1952,23(3):470-472.
[16]亢战,罗阳军.计算结构可靠度指标的修正迭代算法[J].工程力学,2008,25(11):20-26.KANG Zhan,LUO Yang-jun.A modified iteration algorithm for structural reliability index evaluation[J].Engineering Mechanics,2008,25(11):20-26.
