Anti-windup-based Dynamic Controller Synthesis for Lipschitz Systems under Actuator Saturation

Naizhou Wang,Hailong Pei,and Yong Tang

Anti-windup-based Dynamic Controller Synthesis for Lipschitz Systems under Actuator Saturation

Naizhou Wang,Hailong Pei,and Yong Tang

—This paper presents a new method for simultaneous synthesis of dynamic controller and static anti-windup compensator for saturated Lipschitz systems.Thanks to the reformulated Lipschitz property,the Lipschitz systems can be transformed into LPV(linear parameter-varying)systems whose system matrices are affine in a parameter matrix.Based on the modified sector condition dealing with saturation nonlinearity,the design of a nonlinear anti-windup-based controller leads to the solvability of a set of bilinear matrix inequalities(BMI)on the vertices of a bounded convex set which can be solved by the so-called iterative linear matrix inequality(ILMI)algorithm.A numerical example is presented to illustrate the effectiveness of the proposed method.

Naizhou Wang is with the Key Laboratory of Autonomous Systems and Networked Control,Ministry of Education,South China University of Technology,Guangzhou 510640,China,and Key Laboratory of Surface Functional Structure Manufacturing of Guangdong Higher Education Institutes,School of Mechanical and Automotive Engineering,South China University of Technology,Guangzhou 510640,China(e-mail:wangzhou@sina.com).

Hailong Pei is with the Key Laboratory of Autonomous Systems and Networked Control,Ministry of Education,South China University of Technology,Guangzhou 510640,China(e-mail:auhlpei@scut.edu.cn).

Yong Tang is with the Key Laboratory of Surface Functional Structure Manufacturing of Guangdong Higher Education Institutes,School of Mechanical and Automotive Engineering,South China University of Technology, Guangzhou 510640,China(e-mail:ytang@scut.edu.cn). However,this may restrict the improvement of closed-loop performance.In order to pursue better improvement of closedloop performance during the windup,simultaneously design methods of linear controller and static anti-windup compensator are proposed for saturated linear systems in[8-9].Since the knowledge of actuator saturation is incorporated in the design of a linear controller,this approach generally leads to the best closed-loop performance.

Although the vast majority of the anti-windup literature has concentrated on the saturated linear systems,the investigation of anti-windup techniques for nonlinear systems subject to actuator saturation has been constantly focused by the research community[1].We can cite,for instance,[10-11]which consider anti-windup synthesis problems for LPV systems[12];which proposes an adaptive control scheme[13-14];which consider anti-windup synthesis problems for rational systems based on differential algebraic representation(DAR)and linear-fractional representation (LFR)techniques,respectively[15-17];in which the decoupledarchitecture-based anti-windup techniques are proposed for affine nonlinear systems[18];which proposes a dynamic antiwindup scheme for a class of feedback linearizable systems with nonlinear dynamic inversion(NDI)controllers.The intention of most of the enumerated literatures is the extension of anti-windup techniques for linear systems.In order to construct an anti-windup compensator,LMI-based synthesis conditions need to be solved which generally cause conservatism due to the inherent complexity of nonlinear systems.Hence,how to reduce the conservatism when estimating the ROA becomes one of the most important issues.

A particular type of nonlinear systems which has been gaining great attention for several decades is the class of systems which can be represented as a feedback connection of a linear time-invariant(LTI)system and a nonlinear function with certain properties(e.g.,sector-bounded and Lipschitz constraints). Their stability analysis is typically referred to as“absolute stability”which is still of interest in the literature since it is related to many theoretical and practical control problems ([19-24]and references therein).However,most of them do not consider the actuator saturation.Recently,anti-windupbased dynamic controller synthesis problems are investigated for Lur’e and Lipschitz systems[25-26].Asymptotic as well as input-to-output stabilization problems are addressed both in regional and global contexts.More precisely,in[25],Lur’e systems are investigated and the proposed methods can be applied to design simultaneously a nonlinear controller and a static anti-windup compensator;in[26],Lipschitz systems are investigated in which the approaches just allow to synthesize a linear controller.Since the sector-bounded conditions[25]and Lipschitz conditions[26]do not reflect the unique attributes of nonlinearities,the proposed synthesis conditions might causelarge conservatism.

In this paper,simultaneous synthesis of dynamic controller and static anti-windup compensator is investigated for Lipschitz systems subject to actuator saturation.Based on the reformulated Lipschitz property[24],the nonlinear systems can be transformed into LPV systems whose system matrices are affine in a parameter matrix.Using the modified sectorbounded condition dealing with actuator saturation,BMI synthesis conditions are proposed which can be solved by the ILMI optimization procedure[27]at the vertices of a given bounded convex set.Since the reformulated Lipschitz property is less conservative than the traditional one,it is expected that the proposed synthesis method would attain better closed-loop performances than the one in[26].Consider the case that the nonlinearity φ(x)globally satisfies both Lipschitz and sectorbounded conditions.Due to more variable matrices existing in the synthesis conditions,the proposed methods could lead to less conservative optimal or suboptimal results.

The paper is organized as follows.In Section II,the problem to be treated is formally stated,and some useful preliminary results are presented.In Section III,a theoretical foundation on anti-windup-based dynamic controller synthesis is developed. In Section IV,a numerical example is presented to illustrate the effectiveness of the proposed method and at last,some remarks conclude the paper.

II.PROBLEM STATEMENT AND PRELIMINARIES

Consider the following nonlinear systems:

where x∈Rn,vc∈Rm,y∈Rq,z∈Rt,w∈Rlare the states,the control inputs,the measured outputs,the performance outputs and exogenous inputs(reference or disturbance signals).sat(·)is a decentralized saturation function defined as sat(vc)i=sat(vci)=sgn(vci)min(v0i,|vci|), with a saturation level v0i＞0.The function φ(x)∈Rris assumed to satisfy the locally Lipschitz property named as:

A1.For any X,Y∈Bφ={x||xk|≤κk,k= 1,...,n}⊆Rr,the nonlinearity φ(x)satisfies:φ(0)=0 and‖φ(X)-φ(Y)‖≤γφ‖X-Y‖where γφis called the Lipschitz constant.

A2.the exogenous inputs w(t)is bounded in energy,i.e., for some limited scalar λ,w(t)satisfies:

Consider the following nonlinear dynamic controller along with the static anti-windup compensator:

where xc∈Rnis the controller state.The dead-zone function is defined as ψ(vc)=vc-sat(vc).Matrices Ac,Bcφ,Bcu, Cc,Dcφ,Dcu,E1,E2with appropriate dimensions are needed to be determined.The term Eψ(vc)with E=(ET1ET2)Tcorresponds to the static anti-windup loop to mitigate the undesirable effects caused by actuator saturations.

A.Reformulated Lipschitz Property

Throughout the paper,the following lemma will be useful for deriving LMI-based synthesis conditions.

Definition 1[24].Consider two vectors X=(x1,x2,..., xn)Tand Y=(y1,y2,...,yn)T.For all i=1,...,n,an auxiliary vector is defined as XYi=(y1,...,yi,xi+1,...,xn)T. It is also defined that XOi=(0,...,0,xi+1,...,xn)T. Particularly,we have XY0=X,XOn=0.

Lemma 1[24].Considering the function φ:Rn→Rr,the two following items are equivalent:

1)Locally Lipschitz property:φ is locally γφ-Lipschitz with respect to its argument,i.e.,

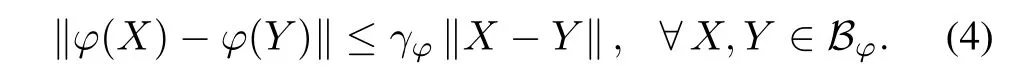
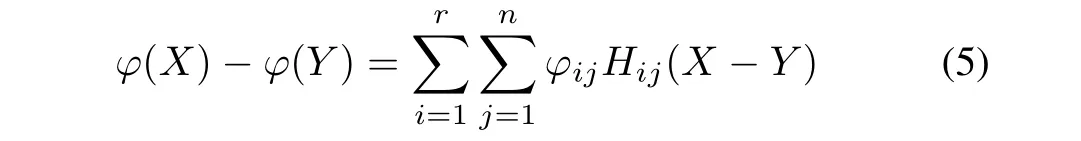
Based on the above Lemma and considering φ(0)=0,the Lipschitz function φ(x)can be represented as:

Lemma 1 provides a less conservative Lipschitz condition compared to the traditional Lipschitz condition(4).For instance,considering two scalar functions φ(x)=sin(x) and φ(x)=tanh(x),the Lipschitz condition(4)does not distinguish between the two nonlinearities.However,with the reformulation(5)and(6),we can see the difference:for φ(x) =sin(x),we have-0.2172≤φ11=sin(x)/x≤1;for φ(x) =tanh(x),we have 0≤φ11=tanh(x)/x≤1.

Corollary 1.Consider a global Lipschitz scalar function φ(x)(with φ(0)=0)which globally satisfies sector-bounded condition:

where K2＞K1≥0.Defining K0=min{K2,γφ},then the following properties hold:

1)(φ(x)-K1x)(φ(x)-K0x)≤0;

2)Θ belongs to a bounded convex set H for which the set of vertices is defined by VH={Ψ∈R|Ψ∈{K1,K0}}.Particularly,if K1=0,we have VH={Ψ∈R|Ψ∈{0,K0}}1Note φ(x)lies in the first and third quadrants and hence φ(x)/x≥0.On the other hand,the Lipschitz condition implies that|φ(x)/x|≤γφ.Then,we have φ(x)/x≤γφ.Considering that φ(x)satisfies the sector-bounded condition,the Corollary 1 can be easily obtained..

B.Modified Sector Condition

Lemma 2[28].Consider the dead-zone nonlinearity ψ(vc), with saturation level v0＞0 and ψ(vc)∈Rmand define the following associated set:

S(vc,v)={vc∈Rm,v∈Rm|-v0≤vc-v≤v0},(10) if(vc,v)is an element of S(vc,v)then the nonlinearity ψ(vc) satisfies the following inequality:

for any diagonal positive-definite matrix T∈Rm×m. Defining now the following system matrices:

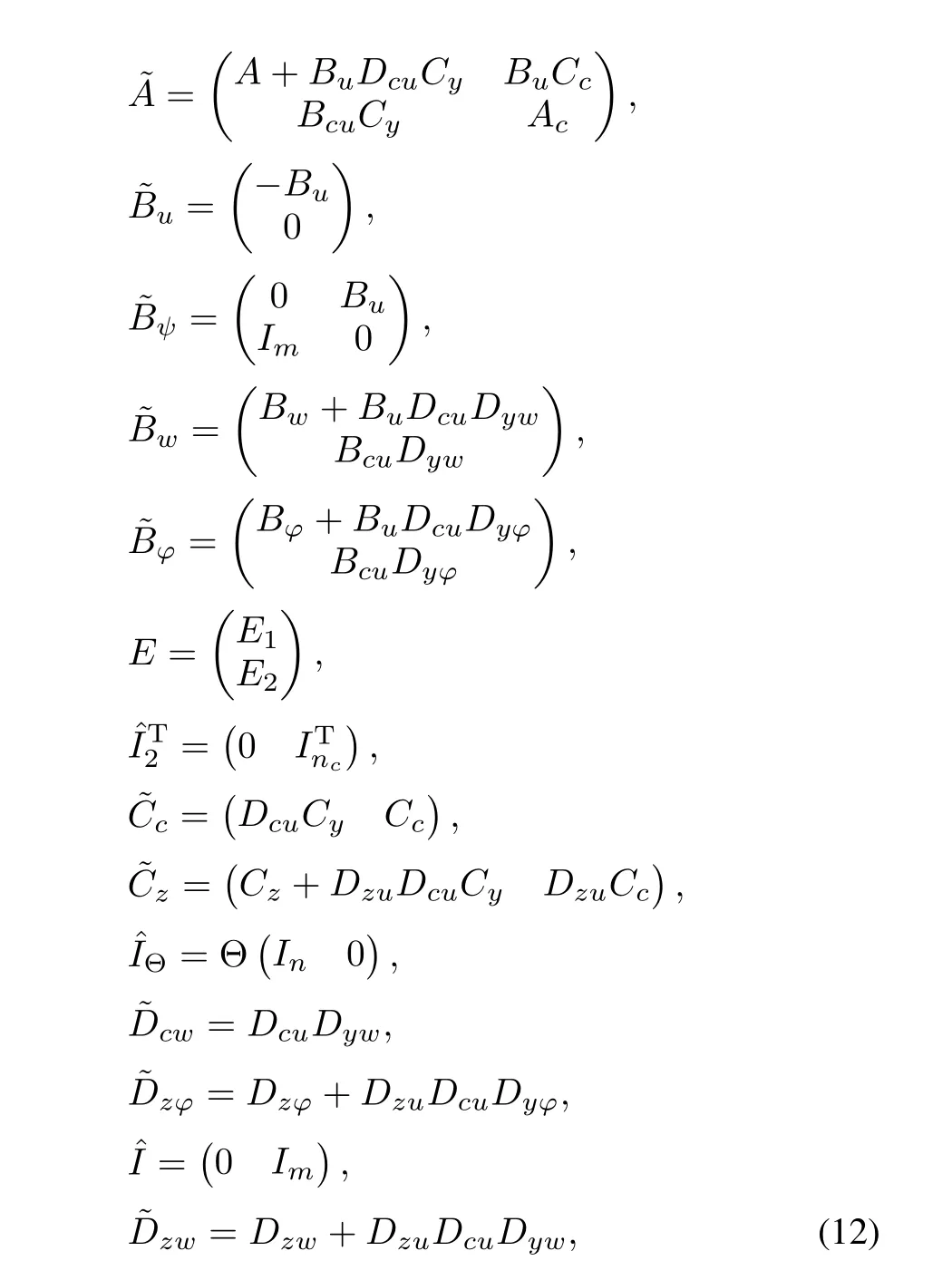
and considering an augmented state vector ξ=(xTxTc)T, the closed-loop system composed of the connection of the nonlinear system(1)and the controller(3)is given as:

In this paper,simultaneous anti-windup and nonlinear controller synthesis problems will be discussed to address the following problems[14,25,29]regarding the closed-loop system (13):

1)Estimate the region of attraction.In the absence of disturbances w(t),we would like to determine an ellipsoid E(P)as large as possible such that the trajectories of the closed-loop system asymptotically converge to the origin with any initial point in it.

2)Determine the L2gain.With a disturbance w(t)satisfying(2),we would like to design an anti-windup-based dynamic controller(3)to ensure the trajectories of the closedloop system remain bounded.Moreover,the L2-gain from the disturbance w(t)to the performance output z(t)should be minimized.

III.MAIN RESULTS

In this section,main result of this paper is shown.Particularly,we present LMI-based conditions for simultaneous synthesis of a nonlinear controller and a static anti-windup compensator for saturated Lipschitz system(1).It is shown that the conditions are in BMI forms.However,the synthesis conditions can be transformed into LMIs if we add some constraints on Bcφand Dcφ.

Define the following polyhedral set:

According to Lemma 2,the following conditions are satis fied:

where,for different matrix Θ∈VH,H(Θ)should be assigned different values and in this way the conservatism of optimization results can be reduced.

Theorem 1.Consider the nonlinear system(1).If there exist two positive-definite matrices P1,W1∈Rn×n,a diagonal positive-definite matrix S1∈Rm×m,matrices Dcu∈Rm×q, H1(Θ)∈Rm×n,Σ1∈Rn×n,Σ2∈Rn×q,Σ3∈Rn×r,Σ4∈Rm×r,Σ5∈Rm×n,Σ6(Θ)∈Rn×m,Σ7∈Rn×m,M2∈Rm×mand positive scalars γ and λ such that the following inequalities are satisfied for all Θ∈VH:

where i=1,...,m,k=1,...,n,τkis the k-th row vector of identity matrix In,

then there exists a controller of the form(3)such that

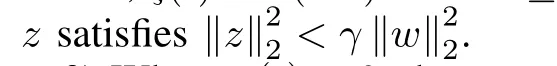
2)When w(t)=0,the corresponding trajectories converge asymptotically to the origin for any initial states belonging to the set E(λP).

Moreover,when variable matrices are obtained,the system matrices in the nonlinear controller(3)can be constructed by:

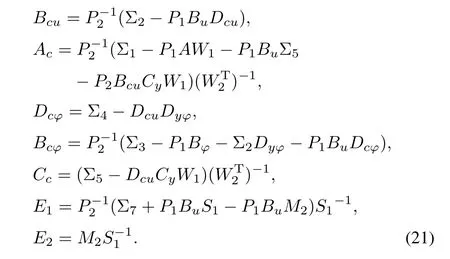
Define new variables as follows:

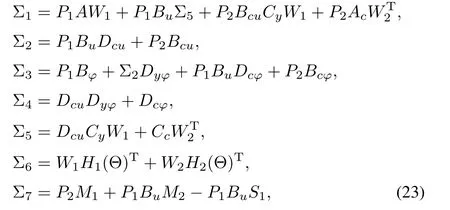
which implies that E(λP)⊆Bφand hence ensures that φ(x)satisfies the Lipschitz condition(4).Pre-and postmultiplying inequality(18)by diag{Π-1,1}and its transpose, respectively,we have:

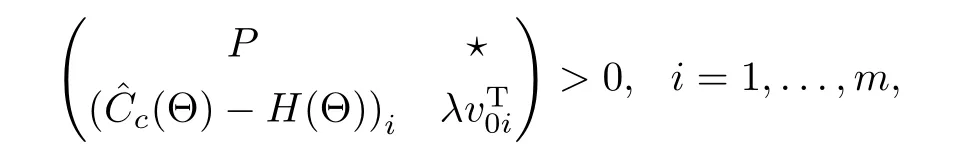
which implies that E(λP)⊆S1and hence the inequality(16) holds.Suppose now that

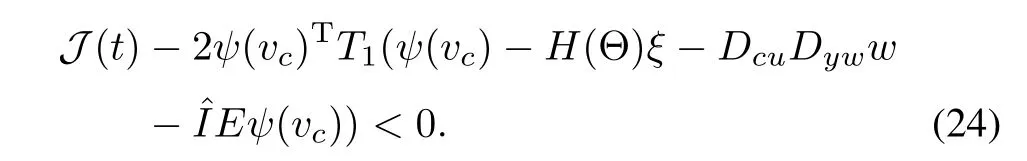
By S-procedure,it follows that J(t)＜0.Applying Schur complement to(24)gives:

Remark 2.The result of Theorem 1 can be applied to treat the case that the nonlinearity φ(x)globally satisfies the Lipschitz condition(4).For this purpose,it suffices to eliminate the inequality(19).

Remark 3.In matrices P,W,“∗”are any matrices such that P W=I2nis verified.

Remark 5.Theorem 1 can also be utilized to synthesize the controller(3)with Bcφ=0 and Dcφ=0.In this case, according to remark 4,BMI conditions have to be solved(even if Dyφ=0).It is pointed out that,under the assumption that Dyφ=0,it is possible to obtain LMI synthesis conditions by the methods proposed in[8](omitted here).However,in this context,it is hard to place the closed-loop poles in a given conic sector(see also Remark 6).

Remark 6.Utilizing the inequalities in Theorem 1 to design the dynamic controller(3)may cause ill-conditioned solutions.In this case,pole placement constraints can be incorporated in the optimization process to obtain a regional and suboptimal solution[33].Considering the eigenvalues of˜A given by xi+iyi,i=1,...,2n,according to[33],if there exists a positive-definite matrix W0such that the following LMIs hold:

Pre-and post-multiplying inequality(26)by matrix Γ and its transpose,we have:

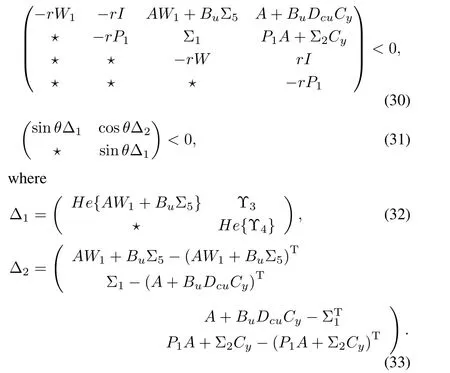
Remark 7.In order to utilize Theorem 1 to estimate the ROA of the close-loop system,the synthesis conditions in Theorem 1 should be modified:set λ=1(without loss of generality);delete the columns and rows related to performance output z(t)and exogenous input w(t).Since the matrix W orPcannot be entirely constructed,we aim at maximizing the region of attraction along the plant state directions(i.e.,E(P1)) by solving the following convex optimization problem[2For the reason thaplease refer to Corollary 1.9]:

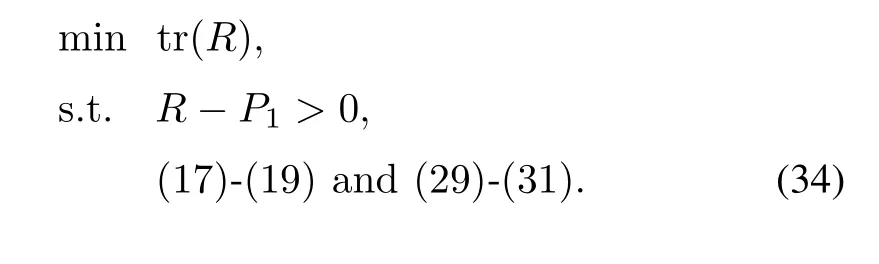
IV.NUMERICAL EXAMPLE

Example 1.Consider the following nonlinear system[25]:

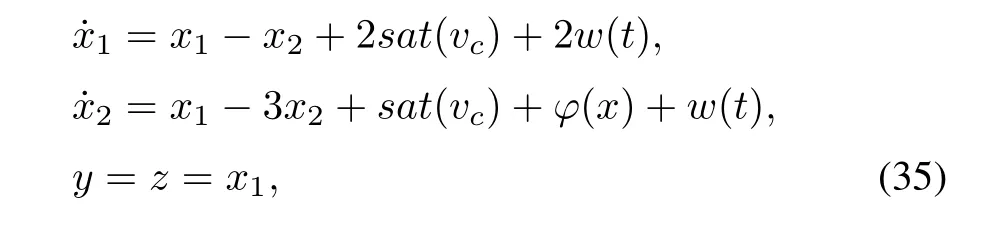
with saturation levelv0=2.

By the traditional Lipschitz method proposed in[26]and sector-bounded method proposed in[24],we obtainγ= 0.5125 andγ=0.2966,respectively.Selecting the disturbance signalw(t)as follows[25]:

The simulation results by the above three methods are shown in Figs.2 and 3.One can easily find that Theorem 1 and the sector-bounded methods have lead to almost the same and nice output responses.However,by the traditional Lipschitz method,bad time responses are obtained.

Consider now the stability analysis problem.An implicit objective in the synthesis of a stabilizing controller is the maximization of the ROA of the closed-loop system.Selectingh= 50,θ=45°and solving the convex optimization problem(34), the obtained results in five cases3Due toDyφ=0,according to Remark 4,Σ3=0 and Σ4=0 imply thatBcφ/=0 andDcφ=0.Solving a set of LMI constraints,we obtain the suboptimal value tr(P1)=0.0615.Then,we initialize the ILMI algorithm by the obtained matrixW1to design two kinds of anti-windup controller(3):Bcφ=0,Dcφ=0;Bcφ/=0,Dcφ/=0.are shown in Table I and Fig.4.Compared with the traditional Lipschitz method[26]and sector-bounded method[25],the method presented in Theorem 1 has led to the largest estimated ROA.Since the regionShas restricted the size ofE(P1),the sector-bounded method leads to large conservatism.Hence,during the synthesis of a dynamic controller,regional inequality condition description should be avoided.

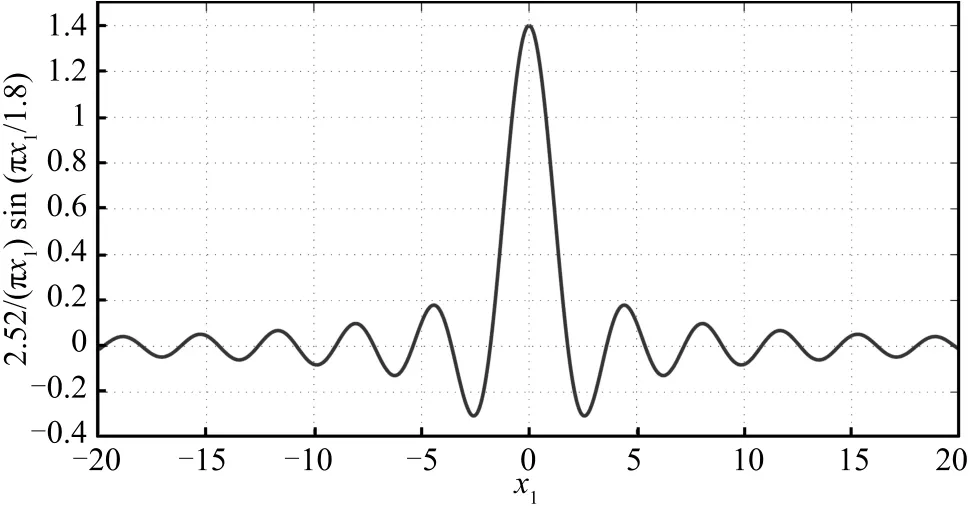
Fig.1.Functionφ11(x).

Fig.2.Time responses of the output by different control strategies.

Fig.3.Time responses of the saturated control signals by different control strategies.

Consider the case that the nonlinearity is given byφ(x)= tanh(1.5x1)which globally satisfies Lipschitz condition(with Lipschitz constantγφ=1.5).It can be verified that the matrix Θ belongs to the set for which the set of vertices is defined byVH={Φ∈R1×2|Φ∈{(0 0),(1.5 0)}}.Selectingh= 100,θ=45°,the estimated ROA in five cases are shown in Fig.5.From the perspective of traditional Lipschitz condition, the Lipschitz constant only increases by 0.1 and hence size of the estimated ROA varies not too much(even thoughthe parameterhis increased)which inevitably causes large conservatism by the method in[26](tr(P1)=0.654In which the minimization ofλimplies the largest disturbance energy that the closed-loop system can tolerate[14].6).On the other hand,φ(x)globally satisfies the sector-bounded condition[25](with Ω=1.5).Hence,no constraints on the size of the ROA need to be considered.The obtained estimated ROA increases greatly(tr(P1)=0.0512).In spite of this,the largest size of the estimated ROA has been obtained by the method proposed in this paper(tr(P1)=0.0491).In Table II,the performances4In which the minimization ofλimplies the largest disturbance energy that the closed-loop system can tolerate[14].under different strategies have been compared.One can easily find,similar as the estimation of ROA,Theorem 1 has led to the best closed-loop performances.

Fig.4.Comparison of estimated region of attractionsIn particular,R1(by Theorem 1R3(by TheoremR5 (traditional Lipschitz method[26]).

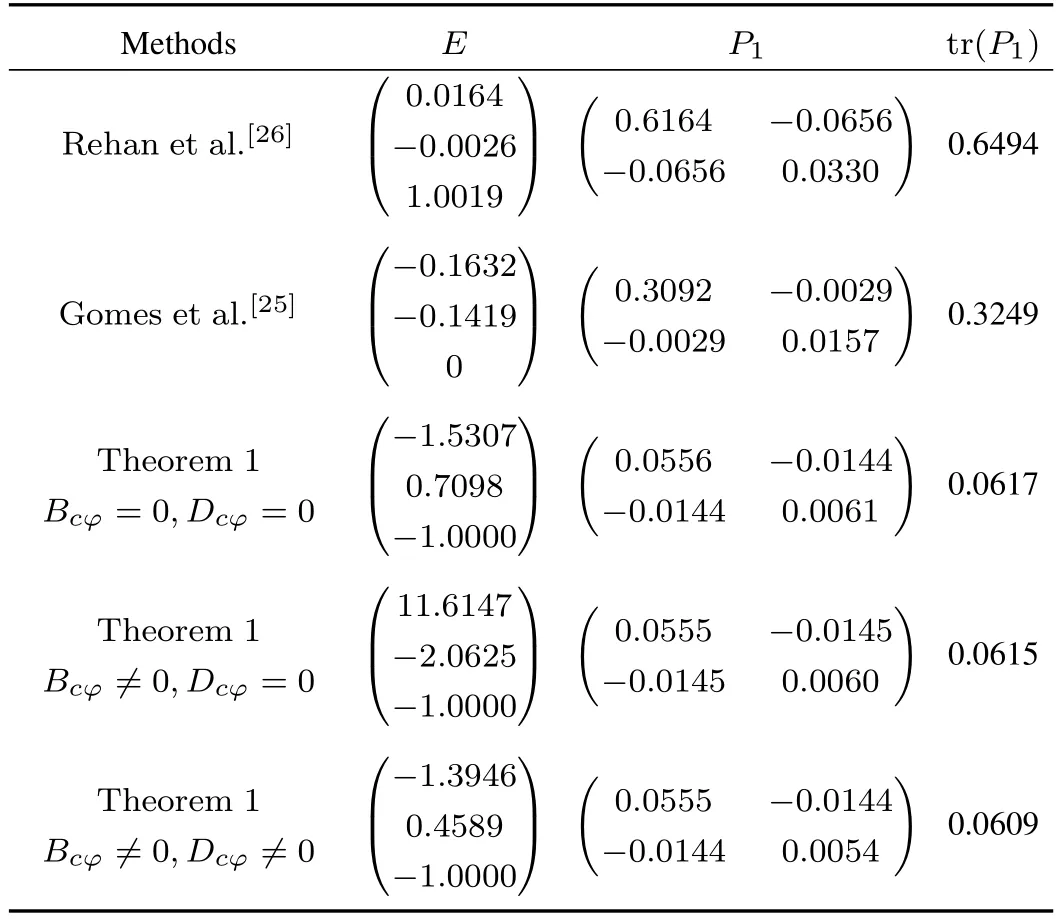
TABLE I COMPARISON OF THE ESTIMATED ROA BY DIFFERENT METHODS

V.CONCLUSION

In this paper,anti-windup-based dynamic controller design techniques have been presented for Lipschitz systems subject to actuator saturation.The methods mainly rely on the socalled reformulated Lipschitz property by which the saturated nonlinear systems can be transformed into LPV systems.With the modified sector-bounded condition tackling the saturation nonlinearity,BMI conditions for the synthesis of an antiwindup-based nonlinear controller are proposed which can be solved at the vertices of a bounded convex set by ILMI optimization procedures(for a certain kind of nonlinear controller, only LMI conditions need to be solved).A numerical example has illustrated the effectiveness of the proposed methods.

Fig.5.Comparison of estimated region of attractions(φ(x)= tanh(1.5x1)).In particular,R1(by Theorem 1 withR2(by Theorem 1 with1 withBcφ=0,Dcφ=0);R4(sector-bounded method[25]);R5 (traditional Lipschitz method[26]).

TABLE II COMPARISON OF PERFORMANCES BY DIFFERENT METHODS

REFERENCES

[1]Tarbouriech S,Turner M C.Anti-windup design:an overview of some recent advances and open problems.IET Control Theory and Applications,2009,3(1):1-19

[2]Teel A R,Kapoor N.TheL2anti-windup problem:its definition and solution.In:Proceedings of the 1997 European Control Conference. Brussels,Belgium:IEEE,1997.1897-1902

[3]Grimm G,Hatfield J,Postlethwaite I,Teel A R,Turner M C,Zaccarian L.Antiwindup for stable linear systems with input saturation:an LMI-based synthesis.IEEE Transactions on Automatic Control,2003,48(9): 1509-1525

[4]Gomes da Silva Jr J M,Tarbouriech S.Antiwindup design with guaranteed regions of stability:an LMI-based approach.IEEE Transactions on Automatic Control,2005,50(1):106-111

[5]Wu F,Soto M.Extended anti-windup control schemes for LTI and LFT systems with actuator saturations.International Journal of Robust and Nonlinear Control,2004,14(15):1255-1281

[6]Turner M C,Herrmann G,Postlethwaite I.Incorporating robustness requirements into antiwindup design.IEEE Transactions on Automatic Control,2007,52(10):1842-1855

[7]Hu T S,Teel A R,Zaccarian L.Stability and performance for saturated systems via quadratic and nonquadratic Lyapunov functions.IEEE Transactions on Automatic Control,2006,51(11):1770-1786

[8]Dai D,Hu T S,Teel A R,Zaccarian L.Output feedback design for saturated linear plants using deadzone loops.Automatica,2009,45(12): 2917-2924

[9]Mulder E F,Tiwari P Y,Kothare M V.Simultaneous linear and antiwindup controller synthesis using multiobjective convex optimization. Automatica,2009,45(3):805-811

[10]Wu F,Grigoriadis K M,Packard A.Anti-windup controller design using linear parameter-varying control methods.International Journal of Control,2000,73(12):1104-1114

[11]Prempain E,Turner M C,Postlethwaite I.Coprime factor based antiwindup synthesis for parameter-dependent systems.Systems and Control Letters,2009,58(12):810-817

[12]Kahveci N E,Ioanou P A,Mirmirani M D.A robust adaptive control design for gliders subject to actuator saturation nonlinearities.In:Proceedings of the 2007 American Control Conference.New York:IEEE, 2007.492-497

[13]Gomes da Silva Jr J M,Oliveira M Z,Coutinho D,Tarbouriech S. Static anti-windup design for a class of nonlinear systems.International Journal of Robust and Nonlinear Control,2014,24(5):793-810

[14]Wang N Z,Pei H L,Wang J,Zhang Q.Anti-windup design for rational systems by linear-fractional representation.IET Control Theory and Applications,2014,8(5):355-366

[15]Teel A R,Kapoor N.Uniting local and global controllers.In:Proceedings of the 4th European Control Conference.Brussels,Belgium,1997.

[16]Morabito F,Teel A R,Zaccarian L.Nonlinear antiwindup applied to Euler-Lagrange systems.IEEE Transactions on Robotics and Automation,2004,20(3):526-537

[17]Rehan M,Hong K S.Decoupled-architecture-based nonlinear antiwindup design for a class of nonlinear systems.Nonlinear Dynamics, 2013,73(3):1955-1967

[18]Herrmann G,Menon P P,Turner M C,Bates D G,Postlethwaite I. Anti-windup synthesis for nonlinear dynamic inversion control schemes. International Journal of Robust and Nonlinear Control,2010,20(13): 1465-1482

[19]Zames G,Falb P L.Stability conditions for systems with monotone and slope restricted nonlinearities.SIAM Journal on Control,1968,6(1):89 -108

[20]Khalil H K.Nonlinear Systems(2nd edition).U.K.:Prentice Hall,1996. [21]Gao J F,Su H Y,Ji X F,Chu J.Stability analysis for a class of neutral systems with mixed delays and sector-bounded nonlinearity.Nonlinear Analysis:Real World Applications,2008,9(5):2350-2360

[22]Phanomchoeng G,Rajamani R,Piyabongkarn D.Nonlinear observer for bounded Jacobian systems,with applications to automotive slip angle estimation.IEEE Transactions on Automatic Control,2011,56(5):1163 -1170

[23]Turner M C,Kerr L M.L2gain bounds for systems with sector bounded and slope-restricted nonlinearities.International Journal of Robust and Nonlinear Control,2012,22(13):1505-1521

[24]Zemouche A,Boutayeb M.On LMI conditions to design observers for Lipschitz nonlinear systems.Automatica,2013,49(2):585-591

[25]Gomes da Silva Jr J M,Castelan E B,Corso J,Eckhard D.Dynamic output feedback stabilization for systems with sector-bounded nonlinearities and saturating actuators.Journal of the Franklin Institute,2013, 350(3):464-484

[26]Rehan M,Khan A Q,Abid M,Iqbal N,Hussain B.Anti-windupbased dynamic controller synthesis for nonlinear systems under input saturation.Applied Mathematics and Computation,2013,220:382-393

[27]Peaucelle D,Arzelier D.An efficient numerical solution for H2static output feedback synthesis.In:Proceedings of the 2001 European Control Conference.Porto Portugal:IEEE,2001.3800-3805

[28]Castelan E B,Tarbouriech S,Queinnec I.Stability and stabilization of a class of nonlinear systems with saturating actuators.In:Proceedings of the 16th IFAC World Congress.Check Republic:IFAC,2005.776-782

[29]Bender F A,Gomes da Silva Jr J M,Tarbouriech S.Convex framework for the design of dynamic anti-windup for state-delayed systems.IET Control Theory and Applications,2011,5(12):1388-1396

[30]Scherer G,Gahinet P,Chilali M.Multiobjective output-feedback control via LMI optimization.IEEE Transactions on Automatic Control,1997, 42(7):896-911

[31]Boyd S,El Ghaoui L,Feron E,Balakrishnan V.Linear Matrix Inequalities in System and Control Theory.Philadelphia,PA:SIAM,1994.

[32]Chilali M,Gahinet P.H∞design with pole placement constraints:an LMI approach.IEEE Transactions on Automatic Control,1996,41(3): 358-367

Naizhou Wang Ph.D.at the College of Automation Science and Engineering,South China University of Technology.His research interests include robust and optimal control,anti-windup control for nonlinear systems.

Hailong Pei Professor at the College of Automation Science and Engineering,South China University of Technology.His research interests include robust control,nonlinear control,embedded system,computer numerical control system,and artificial neural network.Corresponding author of this paper.

Yong Tang Professor at the School of Mechanical and Automotive Engineering,South China University of Technology.His research interests include advanced manufacturing of surface functional structures for thermal control and energy applications.

I.INTRODUCTION

t

December 10,2014;accepted April 5,2015.This work was supported by National Natural Science Foundation of China(61174053), National Key Basic Research Program of China(2014CB845301/2/3),Fundamental Research Funds for the Central Universities(2014ZP0021),Cultivation Fund of the Key Scientific and Technical Innovation Project,Ministry of Education of China(708069),partially by Key Laboratory of Autonomous Systems and Networked Control,Ministry of Education,and Key Laboratory of Surface Functional Structure Manufacturing of Guangdong Higher Education Institutes.Recommended by Associate Editor Haibo Ji.

:Naizhou Wang,Hailong Pei,Yong Tang.Anti-windup-based dynamic controller synthesis for Lipschitz systems under actuator saturation. IEEE/CAA Journal of Automatica Sinica,2015,2(4):358-365

Index Terms—Anti-windup,Lipschitz system,linear matrix inequality(LMI),region of attraction(ROA)

O WING to the fact that real actuator cannot deliver arbitrarily large signals,actuator saturation is generally encountered in engineering practice which may causes large performance degradation,e.g.,lag,limit cycles,overshoot, and even instability of control systems due to the so-called“windup”effects[1].However,for the sake of simplifying the process of a control law design,especially for nonlinear systems due to their inherent complexity,actuator saturation is usually neglected which may cause serious damages and accidents.To mitigate the“windup”effects caused by saturation, a well-established two-step anti-windup approach suggests designing the(linear or nonlinear)dynamic controller a priori and then augmenting it by an anti-windup compensator which only operates when saturation occurs[1-7].Two-step approach is considered attractive in practice because the dynamic controller is designed without consideration of actuator saturation.