A Reduced Reachability Tree for a Class of Unbounded Petri Nets
2015-08-09ShouguangWangSeniorMemberIEEEMengdiGanMengchuZhouFellowIEEEandDanYou
Shouguang Wang,Senior Member,IEEE,Mengdi Gan,Mengchu Zhou,Fellow,IEEE,and Dan You
A Reduced Reachability Tree for a Class of Unbounded Petri Nets
Shouguang Wang,Senior Member,IEEE,Mengdi Gan,Mengchu Zhou,Fellow,IEEE,and Dan You
—As a powerful analysis tool of Petri nets,reachability trees are fundamental for systematically investigating many characteristics such as boundedness,liveness and reversibility. This work proposes a method to generate a reachability tree, called ω RT for short,for a class of unbounded generalized nets called ω -independent nets based on new modified reachability trees(NMRTs).ω RT can effectively decrease the number of nodes by removing duplicate and ω -duplicate nodes in the tree,and verify properties such as reachability,liveness and deadlocks. Two examples are provided to show its superiority over NMRTs in terms of tree size.
Shouguang Wang is with the School of Information and Electronic Engineering,Zhejiang Gongshang University,Hangzhou 310018,China,and also with the State Key Laboratory for Manufacturing Systems Engineering,Xi’an Jiaotong University,Xi’an 710049,China(e-mail:wsg5000@hotmail.com).
Mengdi Gan is with the Ministry of Education(MoE)Key Laboratory of Embedded System and Service Computing,Tongji University,Shanghai 200092,China(e-mail:mengdigan@126.com).
Mengchu Zhou is with the MoE Key Laboratory of Embedded System and Service Computing,Tongji University,Shanghai 200092,China,and also with the Department of Electrical and Computer Engineering,New Jersey Institute of Technology,Newark,NJ 07102-1982,USA(e-mail:zhao@njit.edu).
Dan You is with the School of Information and Electronic Engineering,Zhejiang Gongshang University,Hangzhou 310018,China(e-mail: youdan000@hotmail.com).
In 1969,Karp and Miller[4]developed a finite reachability tree(FRT)method by introducing a special symbol ω,to represent an infinite component in markings resulting from some transition firing loops.FRT is useful in determining such properties as safeness,boundedness,conservativeness,and coverability[6-7].However,it fails to solve deadlocks[20-22], liveness[23],and reachability problems of unbounded nets due to the information loss caused by the use of ω.
Wang[16]proposed a modified reachability tree(MRT) method.An MRT can capture more information about the underlying net than an FRT since it adopts the expression a+bnisuggested by Peterson[7]rather than ω to represent the value of some component of a marking.Later,a computer program for the automated generation of an MRT for a Petri net was developed in[24].Jeng and Peng[13-14]extended the capability of FRT for determining liveness,and proposed an augmented reachability tree(ART),which is applicable to oneplace-unbounded nets only.
Wang et al.[17]formalized and improved their previous results in[16]with a proof for the finiteness of an MRT and its usefulness in solving reachability,deadlock and liveness problems.Their work sets a milestone toward the solution of this long-standing problem.However,the set of markings represented by the nodes of an MRT is not necessarily equal to that of reachable markings[12,15].Wang et al.proposed an improved reachability tree(IRT)for one-place-unbounded nets in[19].The set of markings represented by an IRT is equal to that of reachable markings.
Motivated by the aforementioned work,Wang et al.[18]proposed a new modified reachability tree(NMRT)method for ω-independent unbounded nets,which has a larger application scope than all the existing methods.An NMRT consists of only but all reachable markings from its initial marking and can correctly check deadlocks.However,it still suffers from a problem that the number of nodes in the tree grows rapidly with respect to the net size.
In order to decrease the number of nodes in a reachability tree,this work proposes a reduced reachability tree for ωindependent nets based on NMRTs,and we call it an ωRT for short.The ωRT removes duplicate and ω-duplicate nodes in the tree such that the number of nodes decreases.The rest of this paper is organized as follows.Section II briefly reviewspreliminaries used in this paper.AnωRT construction algorithm is presented in Section III.Section IV provides an example for the proposed method to illustrate its superiority. Finally,conclusions are presented in Section V.
II.PRELIMINARIES
In the remaining discussion,assumeZ,N,andN+,denote the set of integers,nonnegative integers,and positive integers, respectively.
A.Basics of Petri Nets
The following basics of Petri nets(PNs)are due to[5-7].
A generalized PN is a 4-tupleN=(P,T,F,W),wherePandTare finite,non-empty,and disjoint sets.Pis the set of places andTis the set of transitions withP∪T/=∅andP∩T=∅.F⊆(P×T)∪(T×P)is called a flow relation of the net,represented by arcs with arrows from places to transitions or from transitions to places.Wis a mapping that assigns a weight to an arc:W(x,y)>0 if(x,y)∈F,andW(x,y)=0 otherwise,where,x,y∈P∪T.
A markingµrepresents a system state,which shows the number of tokens contained in each placep∈P.The initial marking is denoted asµ0.A transitiont∈Tis enabled atµif∀p∈·t,µ(p)≥W(p,t).The fact is denoted byµ[t〉.Firing it yields a new markingµ′such that∀p∈P,µ′(p)=µ(p)-W(p,t)+W(t,p),as denoted byµ[t〉µ′.µ′is called an immediately reachable marking fromµ.µ′′is said to be reachable fromµif there exists a sequence of transitionsσ=t0t1...tnand markingsµ1,µ2,...,andµnsuch thatµ[t0〉µ1[t1,...,µn[tn〉µ′′holds.The set of markings reachable fromµ0inNis called the reachability set of(N,µ0) and denoted byR(N,µ0).
Given a PN(N,µ0),t∈Tis live atµ0if∀µ∈R(N,µ0),∃µ′∈R(N,µ),µ′[t〉.(N,µ0)is live if∀t∈T,tis live atµ0. (N,µ0)is dead atµ0if∄t∈T,µ0[t〉.(N,µ0)is deadlockfree(weakly live or live-locked)if∀µ∈R(N,µ0),∃t∈T,µ[t〉.It is bounded if∃k∈N+,∀µ∈R(N,µ0),∀p∈P,µ(p)≤k.It is said to be unbounded if it is not bounded.
B.ω-number
The definitions and notations ofω-numbers in this subsection are from[16-18].
1)ω-number.A subset of integersSis called anω-number if∃k∈N+,n,q∈Zsuch thatS={ik+q|i≥n,0≤q<k}.Scan be expressed uniquely asS=ω(k,n,q)≡k ωn+q≡{ik+q|k∈N+,n∈Z,0≤q<k,i≥n},whereω(k,n,q)orkωn+qis called a canonicalω-number withkas its base,nthe last bound,andqthe remainder.
2)Addition ofω-number and integers.Given anω-numberω(k,n,q)and an integera∈Z,it is defined thatω(k,n,q)+a=ω(k,n+s,r),whereq+a=sk+r,s∈Z,0≤r<k.
3)Comparison of twoω-numbers.LetZωbe the set of integers andω-numbers.∀a,b∈Z,a≤bis defined as eithera,b∈Zωanda≤bora=ω(k,m,q),b=ω(k,n,q),andm≤n.Note that in the second case,bis a subset ofa,i.e.,a⊇b,if both can be viewed as sets.
4)Comparison of twoω-vectors.A vectorx∈Znωis called anω-vector if at least one of its elements is anω-number. Note that ifxhas noω-number,it is simply ann-dimensional integer vector,i.e.,x∈Zn.A markingµis called anωmarking if it can be represented by anω-vector.Anω-marking can be viewed as a set of ordinary markings.Anω-markingais less than or equal tob(oracontainsb)ifaandbhave the same non-ω-number coordinates,and the other coordinates ofaare less than or equal to the ones ofb.
C.NMRT
Following[18],we give the following definitions.
Definition 1.At anω-markingµthat is a set of ordinary markings,t∈Tis enabled iftis enabled at each ordinary marking inµ;tis not enabled atµiftis not enabled at any ordinary marking inµ;tis conditionally enabled atµif it is not enabled at some ordinary markings inµbut enabled at any other ordinary marking inµ.
In the remaining discussion,assume that the next-state marking functionδ(µ,t)is the marking resulting from firingtatµ.
Definition 2.Given a markingµandt∈T,
1)Ifµis an ordinary marking andtis enabled atµ,thenδ(µ,t)is computed by using the transition firing rule for ordinary markings;
E-HOUSE基本框架为全钢结构,外部墙面和屋顶为铆焊结合和喷漆。底盘采用H型钢、槽钢,材质为Q345B。E-HOUSE的设计、生产、安装、调试均在生产工厂内完成,在用户安装位置仅进行E-HOUSE的地脚安装、外部进出线电缆连接,即可进行设备试验、试运行、投运。
2)Ifµis anω-marking andtis enabled atµ,thenδ(µ,t) is computed by using the transition firing rule for ordinary markings and the addition ofω-numbers and integers;
3)Ifµis anω-marking andtis conditionally enabled atµ, thenδ(µ,t)is computed as follows:
a)Letµ′be anω-marking derived fromµby removing each ordinary marking ofµat whichtis not enabled;
b)Letδ(µ,t)=δ(µ′,t),whereδ(µ′,t)is computed in the same way as 2).
Definition 3.Letxandzbe two nodes in an NMRT,whereµzis the marking resulting from firing transitiontat the current markingµxandµz/=δ(µx,t).µzis calledω-dependent if there exists a nodeyon the path from the root node tozsuch that 1)δ(µx,t)>µyand 2)at least two components inδ(µx,t)are larger than the corresponding ones inµy.
Definition 4.Given an unbounded PN(N,µ0)and its NMRT obtained by the algorithm in[18].(N,µ0)is calledω-independent if its NMRT does not contain anyω-dependent markings.Otherwise,it is calledω-dependent.
For example,in Fig.1(b),µ2=(ω1,ω1)is anω-dependent marking sinceµ2/=δ(µ0,t2),δ(µ0,t2)=(1,1)>(0,0)andtwo components in(1,1)are larger than those respective ones in(0,0).Similarly,µ4can be verified to be anω-dependent marking.Therefore,the net in Fig.1(a)isω-dependent.While, the net in Fig.2(a)isω-independent since its NMRT contains noω-dependent markings.
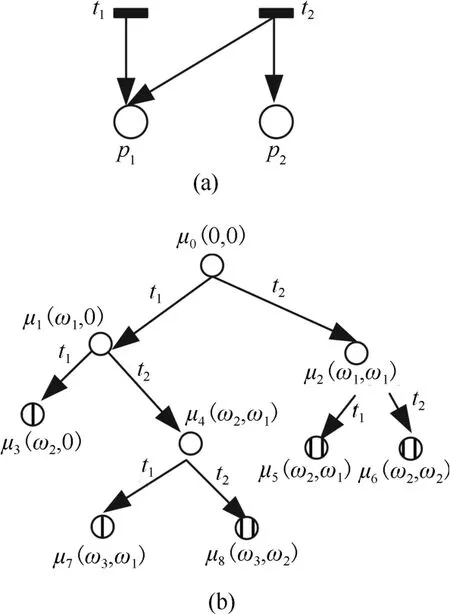
Fig.1.(a)Anω-dependent unbounded net and(b)Its NMRT.
III.GENERATION OF REDUCED REACHABILITY TREES
To describe anωRT,four types of nodes are introduced including:terminal,duplicate,ω-duplicate and common nodes pictured by the circle with oblique lines,the filled circle,the circle with vertical lines and the hollow circle,respectively. A terminal node is a node corresponding to a dead marking without any enabled transitions.The definitions of duplicate andω-duplicate nodes are as follows.
Definition 5.Letxwith a markingµxbe a current node of anωRT.It is called a duplicate node ifµxhas been computed previously during the procedure of constructing anωRT.
Definition 6.Letxwith anω-markingµxbe a current node of anωRT.It is called anω-duplicate node ifµxcan be contained by anω-markingµyof another node that was computed previously during the procedure of constructing anωRT.
Remark 1.These concepts of“duplicate”and“ω-duplicate nodes”are first proposed in[17]and used in the algorithm proposed in[18].As stated in[17-18],a duplicate node is a node with a marking that previously appears in the tree along the same path and anω-duplicate node is a node with aω-marking that is contained by another node that appears previously in the tree along the same path.Note that in this paper,duplicate andω-duplicate nodes in generating anωRT is based on these modified definitions.
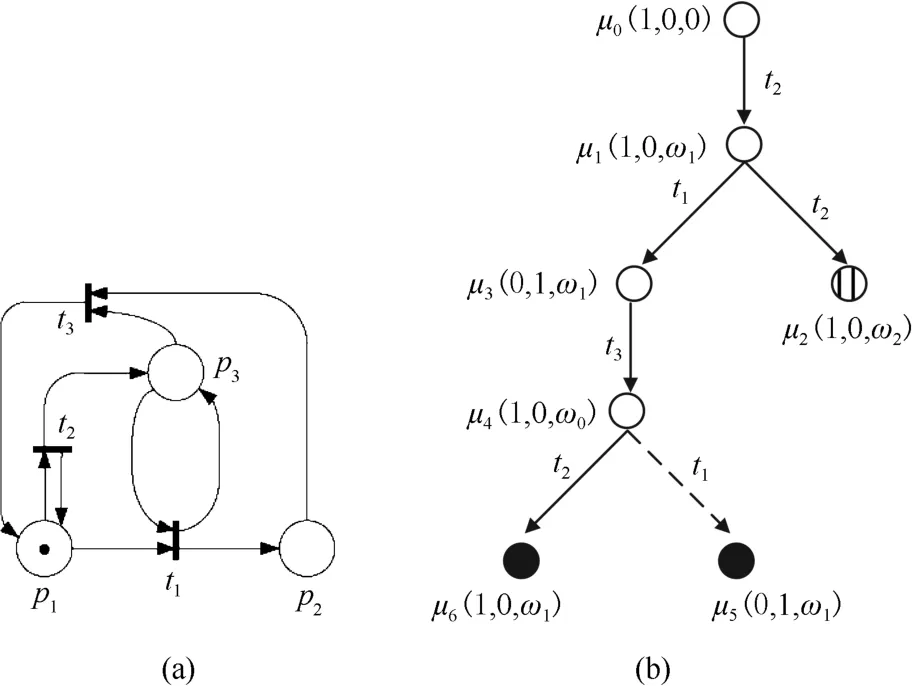
Fig.2.(a)Anω-independent unbounded net and(b)Its NMRT.
AnωRT construction algorithm forω-independent nets based on NMRTs is stated as follows.
Algorithm 1.Construction algorithm forωRT
Input:Anω-independent PN(N,µ0).
Output:AnωRT.
1)Letx0be the root node of theωRT andµ0be the marking of nodex0;
2)Initialize the stack Λ:=(x0)and the set Ξ:=µ0;
/*Λ is a stack consisting of common nodes and Ξ a set containing all the markings of nodes that have appeared in the tree computed by this algorithm*/
3)whileΛ/=()do
4)x:=pop(Λ);
/*Remove the last nodexfrom the stack.*/
5)Letµxbe the marking of nodex;
6)foreacht∈Tdo
7)iftis enabled or conditionally enabled atµxthen
8)Compute the next-state functionδ(µx,t)by
Definition 2 and create a new nodez;
9)ifthere exists a nodeyin the path fromx0tox
withδ(µx,t)>µythen
10)foreachp∈Pdo
11)ifδ(µx,t)p>(µy)pandδ(µx,t)p∈N then
12)(µz)p:=ω(k,n,q),wherek=δ(µx,t)p-(µy)p,
δ(µx,t)p=nk+q,and 0≤q<k;
13)else
14)(µz)p:=δ(µx,t)p;
15)end if
16)end for
17)else
18)µz:=δ(µx,t);
19)end if
20)Ξ:=Ξ∪µz;
21)ifzis a common nodethen
22)Λ:=push(Λ,z);
/*Push nodezinto stack Λ as the last node in Λ.*/
23)end if
24)iftis enabled atµxthen
25)Add a solid arc t from x to z;
/*A solid arc indicates that t is enabled atµx.*/
26)else
27)Add a dotted arc t from x to z;
/*A dotted arc indicates that t is conditionally enabled at µx.*/
28)end if
29)end if
30)end for
31)end while
32)end.
Given an ω-independent net,its ωRT can be constructed by Algorithm 1.We briefly explain this algorithm as follows. First,let x0be the root node of an ωRT andµ0(0,0)the marking of x0,Ξ={µ0},Λ=(x0).Second,remove the last node from a stack Λ,and then obtain the current markingµx. Third,for each t∈T that is enabled or conditionally enabled atµx,compute the next-state δ(µx,t)by Definition 2,and then obtain the next-state markingµzaccording to the rule proposed in this paper.Finally,a new node z is created and is pushed into Λ if it is a common node.Repeat these steps until Λ is empty and an ωRT is hence constructed.
Compared with NMRT,ωRT can decrease the number of nodes in the reachability tree by eliminating more duplicate and ω-duplicate nodes that have been computed already.An ω-independent unbounded net with two unbounded places is shown in Fig.3(a)and(b)is its NMRT with 35 nodes.It is easy to see that more than a half of nodes are reduced by using ωRT since its ωRT shown in Fig.3(c)has only 17 nodes.Clearly,our method successfully decreases the number of nodes in the reachability tree.
B.Applications of ωRT
The following theorems guarantee the finiteness of ωRTs and their usefulness in determining reachability,deadlocks, and liveness of ω-independent unbounded PNs.
Theorem 1(Finiteness).The ωRT of an ω-independent unbounded Petri net is finite.
Proof.It has been proved that an NMRT is finite in[18].As shown earlier,an NMRT just removes some duplicate nodes with markings that previously appear in the path from the root node to the current node and ω-duplicate nodes with ωmarkings that are contained by another node in the path from the root node to the current node.While an ωRT removes some duplicate nodes with markings that previously appear in the whole tree and ω-duplicate nodes with ω-markings that are contained by another node in the tree.Clearly,the number of nodes in an ωRT is smaller than that in an NMRT.Therefore, the conclusion holds.□
Theorem 2(Reachability).The ωRT of an ω-independent unbounded Petri net consists of only but all reachable markings from its initial marking.
Proof.It has been proved in[18]that the NMRT of an ω-independent unbounded Petri net consists of all and only reachable markings from its initial marking.Hence,we only need to prove that the ωRT represents the same marking set as the NMRT for the ω-independent unbounded Petri net. Obviously,we can transform the NMRT into the ωRT by eliminating some duplicate and ω-duplicate nodes that have been computed in the NMRT.Hence,the ωRT represents the same marking set as the NMRT.Therefore,we can conclude that the ωRT of an ω-independent unbounded Petri net consists of only but all reachable markings from its initial marking.□
Theorem 3(Deadlock-checking).An ω-independent unbounded Petri net has deadlocks if and only if its ωRT contains terminal nodes or full conditional nodes.
Proof.Sufficiency:By the definition of terminal nodes or full conditional nodes,we can conclude that there exists a dead marking in terminal nodes or full conditional nodes.Since the ωRT contains terminal nodes or full conditional nodes, there exists a dead marking in the ωRT.Hence,there exists a dead marking in the ω-independent unbounded Petri net by Theorem 2.Therefore,the ω-independent unbounded Petri net has deadlocks.
Necessity:By Theorem 2,there exists a dead marking in the ωRT,since the ω-independent unbounded Petri net has deadlocks.Obviously,only terminal nodes or full conditional nodes contain dead markings for all nodes in the ωRT.Hence, the ωRT contains terminal nodes or full conditional nodes.□
IV.EXAMPLE
An illustrative example is presented in this section to show the superiority of ωRT.An ω-independent unbounded net with three unbounded places is shown in Fig.4(a)and its ωRT is shown in(b).We can see that there are only 65 nodes in its ωRT.However,there are more than 600 nodes in its NMRT.Due to the space limit,we do not present its NMRT and more details about its NMRT are in Appendix.Trivially, the number of nodes in its ωRT is much smaller than that in its NMRT.This example illustrates that our method can drastically decrease the number of nodes in a reachability tree by eliminating numerous duplicate and ω-duplicate nodes in the tree.Besides,our method can avoid spurious markings and can correctly check deadlocks for ω-independent nets. According to Theorem 3,it is easy to see that the net in Fig.4(a)is deadlock-free.
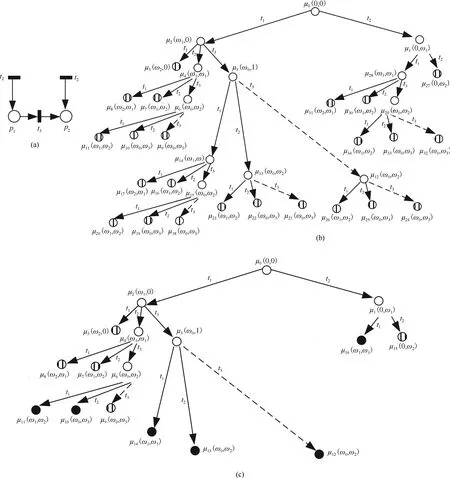
Fig.3.(a)An ω-independent unbounded net with two unbounded places,(b)Its NMRT,and(c)Its ωRT.
V.CONCLUSION
How to establish a finite reachability tree to solve reachability problems of arbitrary unbounded nets has remained an open problem since the inception of Petri nets half a century ago[25-27].Due to its extreme difficulty,only limited progress has been made.
In this work,we propose a reduced reachability tree called ωRT for ω-independent nets based on new modified reachability trees.It can drastically decrease the number of nodes by removing some duplicate nodes and ω-duplicate nodes in the tree.Furthermore,ωRT can be used to determine some properties such as reachability,liveness and deadlocks as well.
Since the method proposed in this paper can be applicable for ω-independent nets only,future work should extend the proposed results to more general classes of Petri nets.Additional efforts to reduce such tree size should be made,e.g., by allowing the net to fire multiple transitions whenever no conflicts are involved.Computer aided design tools should be developed to facilitate the applications of the proposed finite trees to such application fields as industrial hybrid systems, Internet-based game systems,Internet of things and Internet of vehicles[28-30].
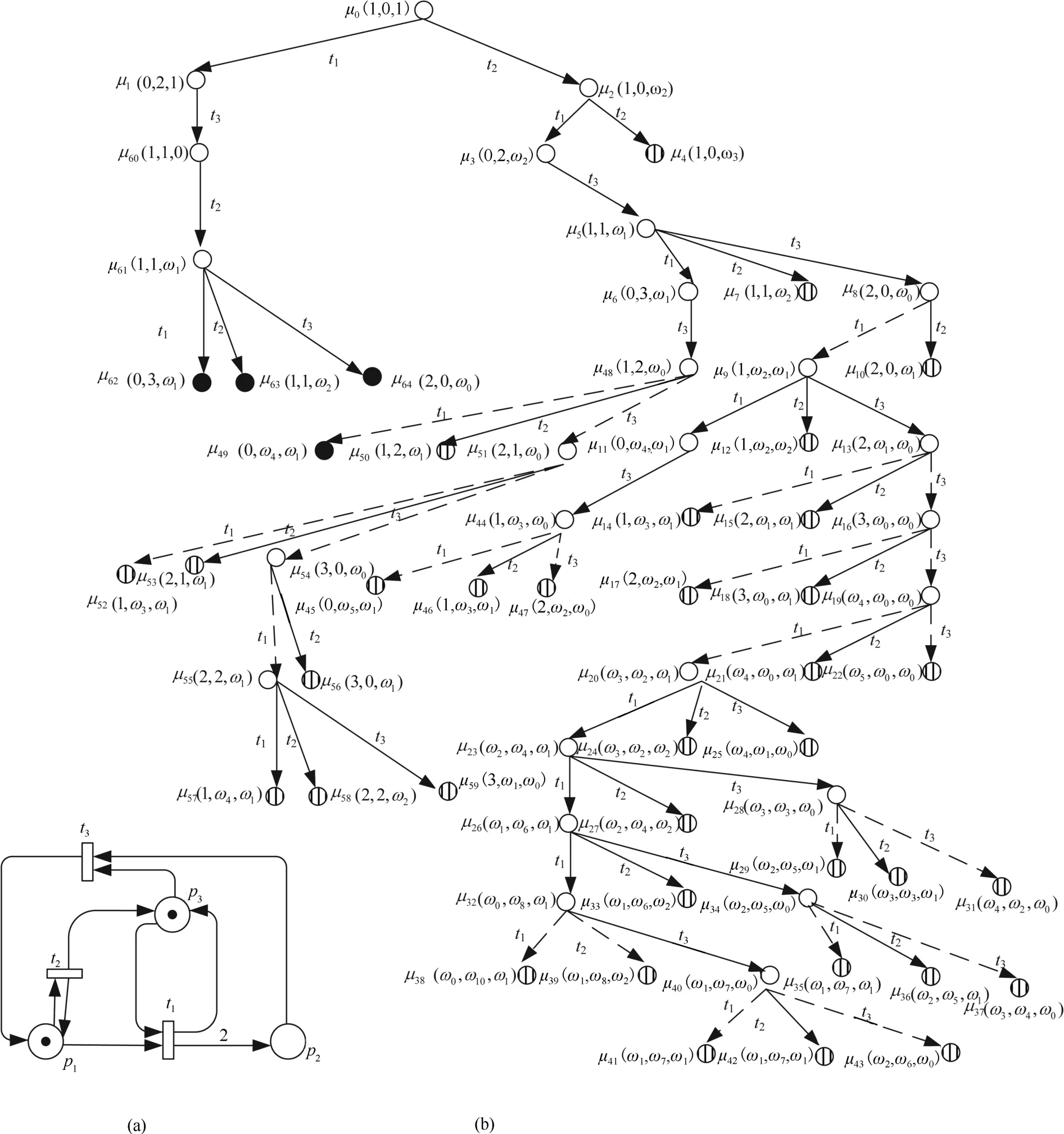
Fig.4.(a)An ω-independent unbounded net with three unbounded places and(b)Its ωRT.
REFERENCES
[1]Hrz B,Zhou M C.Modeling and Control of Discrete-Event Dynamic Systems.London,UK:Springer,2007.
[2]Ding Z H,Zhou M C,Wang S G.Ordinary differential equationbased deadlock detection.IEEE Transactions on Systems,Man,and Cybernetics:Systems,2014,44(10):1435-1454
[3]Hu H S,Zhou M C.A Petri net-based discrete-event control of automated manufacturing systems with assembly operations.IEEE Transactions on Control Systems Technology,2015,23(2):513-524
[4]Karp R M,Miller R E.Parallel program schemata.Journal of Computer and System Sciences,1969,3(2):147-195
[5]Li Z W,Zhou M C.Deadlock Resolution in Automated Manufacturing Systems:a Novel Petri Net Approach.London:Springer,2009.
[6]Murata T.Petri nets:properties,analysis and applications.Proceedings of the IEEE,1989,77(4):541-580
[7]Peterson J L.Petri Net Theory and the Modeling of Systems.NJ: Prentice-Hall,1981.
[8]Wu N Q,Zhou M C,Chu F,Mammar S.Modeling,analysis,scheduling, and control of cluster tools in semiconductor fabrication.Contemporary Issues in Systems Science and Engineering.Hoboken,NJ:Wiley/IEEE Press,2015.289-315
[9]Yang F J,Wu N Q,Qiao Y,Zhou M C.Petri net-based optimal one-wafercyclic scheduling of hybrid multi-cluster tools in wafer fabrication.IEEE Transactions on Semiconductor Manufacturing,2014,27(2):192-203
[10]Zhou M C,Dicesare F.Petri Net Synthesis for Discrete Event Control of Manufacturing Systems.London:Kluwer Academic Publishers,1993.
[11]Zhou M C,Venkatesh K.Modeling,Simulation and Control of Flexible Manufacturing Systems:A Petri Net Approach.Singapore:World Scientific,1998.
[12]Ding Z J,Jiang C J,Zhou M C.Deadlock checking for one-place unbounded Petri nets based on modified reachability trees.IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics,2008, 38(3):881-883
[13]Jeng M D Peng M Y.On the liveness problem of 1-place-unbounded Petri nets.In:Proceedings of the 1997 IEEE International Conference on Systems,Man,and Cybernetics,Computational Cybernetics and Simulation.Orlando,FL:IEEE,1997.3221-3226
[14]Jeng M D,Peng M Y.Augmented reachability trees for 1-placeunbounded generalized Petri nets.IEEE Transactions on Systems,Man, and Cybernetics,Part A:Systems and Humans,1999,29(2):173-183
[15]Ru Y,Wu W W,Hadjicostis C N.Comments on a modified reachability tree approach to analysis of unbounded Petri nets.IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics,2006,36(5):1210
[16]Wang F Y.A modified reachability tree for Petri nets.In:Proceedings of the 1999 IEEE International Conference on Systems,Man,and Cybernetics.Charlottesville,VA:IEEE,1991.329-334
[17]Wang F Y,Gao Y Q,Zhou M C.A modified reachability tree approach to analysis of unbounded Petri nets.IEEETransactionsonSystems,Man, and Cybernetics,Part B:Cybernetics,2004,34(1):303-308
[18]Wang S G,Zhou M C,Li Z W,Wang C Y.A new modified reachability tree approach and its applications to unbounded Petri nets.IEEE Transactions on Systems,Man,and Cybernetics:Systems,2013,43(4): 932-940
[19]Wang Y H,Jiang B,Jiao L.Property checking for 1-place-unbounded Petri nets.In:Proceedings of the 4th IEEE International Symposium on Theoretical Aspects of Software Engineering(TASE).Taipei,China: IEEE,2010.117-125
[20]Fu Jian-Feng,Dong Li-Da,Xu Shan-Shan,Zhu Dan,Zhu Cheng-Cheng. An improved liveness condition for S4P R nets.ActaAutomaticaSinica, 2013,39(9):1439-1446(in Chinese)
[21]Li Z W,Wang A R.A Petri net based deadlock prevention approach for flexible manufacturing systems.Acta Automatica Sinica,2003,29(5): 733-740
[22]Xing Ke-Yi,Tian Feng,Yang Xiao-Jun,Hu Bao-Sheng.Polynomialcomplexity deadlock avoidance policies for automated manufacturing systems.Acta Automatica Sinica,2007,33(8):893-896(in Chinese)
[23]Wang S G,Gan M D,Zhou M C.Macro liveness graph and liveness of ω-independent unbounded nets.Science China Information Sciences, 2015,58(3):032201
[24]Wong H M,Zhou M C.Automated generation of modified reachability trees for Petri nets.In:Proceedings of the 1992 Regional Control Conference.Brooklyn,NY,1992.119-121
[25]Huang Y S,Pan Y L,Zhou M C.Computationally improved optimal deadlock control policy for flexible manufacturing systems.IEEE Transactions on Systems,Man,and Cybernetics,Part A:Systems and Humans, 2012,42(2):404-415
[26]Huang Y S,Weng Y S,Zhou M C.Modular design of urban traffic-light control systems based on synchronized timed Petri nets.IEEE Transactions on Intelligent Transportation Systems,2014,15(2):530-539
[27]Pan L,Ding Z J,Zhou M C.A configurable state class method for temporal analysis of time Petri nets.IEEETransactionsonSystems,Man, and Cybernetics:Systems,2014,44(4):482-493
[28]Cheng J J,Cheng J L,Zhou M C,Liu F Q,Gao S C,Liu C.Routing in internet of vehicles:a review.IEEE Transactions on Intelligent Transportation Systems,to be published
[29]Ding Z H,Zhou Y,Jiang M Y,Zhou M C.A new class of Petri nets for modeling and property verification of switched stochastic systems.IEEE Transactions on Systems,Man,and Cybernetics:Systems,2015,45(7): 1087-1100
[30]Lee J S,Zhou M C,Hsu P L.Multiparadigm modeling for hybrid dynamic systems using a Petri net framework.IEEE Transactions on Systems,Man,and Cybernetics:Part A:Systems and Humans,2008, 38(2):493-498
Shouguang Wang received the Ph.D.degree from the College of Electrical Engineering,Zhejiang University,China in 2005.He is currently a professor at the School of Information and Electronic Engineering,Zhejiang Gongshang University.He was a a visiting professor with the Department of Electrical and Computer Engineering,New Jersey Institute of Technology,Newark,NJ,from Jan.2011 to Jan. 2012.He is a visiting professor with the Electrical and Electronic Engineering Department,University of Cagliari,Cagliari,Italy,from Dec.2014 to Dec.2015.He was the Dean of the Department of Measuring and Control Technology and Instrument from July 2011 to July 2014.He is a senior member of IEEE.
His research interests include application,supervisory control of discrete event systems,Petri net theory and application,and production scheduling. He is the author or coauthor of over 50 published papers.


Mengdi Gan received the bachelor degree from the School of Information and Electronic Engineering,Zhejiang Gongshang University,China in 2014. She is currently a master student at the School of Electronic and Information Engineering,Tongji University.Her research interests include supervisory control of discrete event systems,and Petri net theory and application.
Mengchu Zhou(S88-M90-SM93-F03)received his B.S.degree in control engineering from Nanjing University of Science and Technology,Nanjing, China in 1983,M.S.degree in automatic control from Beijing Institute of Technology,Beijing,China in 1986,and Ph.D.degree in computer and systems engineering from Rensselaer Polytechnic Institute, Troy,NY,USA in 1990.He joined New Jersey Institute of Technology(NJIT),Newark,NJ in 1990, and is now a Distinguished Professor of Electrical and Computer Engineering.His research interests are in Petri nets,Internet of Things,big data,semiconductor manufacturing,transportation,and energy systems.He has over 600 publications including 12 books,300+journal papers(majority in IEEE Transactions),and 28 book-chapters.His recently co-authored/edited books include Business and Scientific Workflows:A Web Service-Oriented Approach,IEEE/Wiley,New Jersey,2013(with W.Tan)and Contemporary Issues in Systems Science and Engineering,IEEE/Wiley,New Jersey,2015(with H.-X.Li and M.Weijnen).

He was invited to lecture in Australia,Canada,China(Mainland,Hong Kong,and Taiwan),France,Germany,Italy,Japan,Korea,Mexico,Singapore, and US and served as a plenary speaker for many conferences.He is the founding Editor of IEEE Press Book Series on Systems Science and Engineering.He served as Associate Editor of IEEE Transactions on Robotics and Automation from 1997 to 2000 and IEEE Transactions on Automation Science and Engineering from 2004-2007,and Editor of IEEE Transactions on Automation Science and Engineering from 2008-2013.He is Associate Editor of IEEE Transactions on Systems,Man,and Cybernetics:Systems, IEEE Transactions on Industrial Informatics and IEEE Transactions on Intelligent Transportation Systems.He served as Guest-Editor for many journals including IEEE Transactions on Industrial Electronics and IEEE Transactions on Semiconductor Manufacturing.He was General Chair of IEEE Conf.on Automation Science and Engineering,Washington D.C.,August 23-26,2008, General Co-Chair of 2003 IEEE International Conference on System,Man and Cybernetics(SMC),Washington DC,October 5-8,2003,Founding General Co-Chair of 2004 IEEE Int.Conf.on Networking,Sensing and Control, Taipei,March 21-23,2004,and General Chair of 2006 IEEE Int.Conf.on Networking,Sensing and Control,Ft.Lauderdale,Florida,U.S.A.April 23-25,2006.He was Program Chair of 2010 IEEE International Conference on Mechatronics and Automation,August 4-7,2010,Xi’an,China,1998 and 2001 IEEE International Conference on SMC and 1997 IEEE International Conference on Emerging Technologies and Factory Automation.He organized and chaired over 100 technical sessions and served on program committees for many conferences.
Dr.Zhou has led or participated in over 50 research and education projects with total budget over 12M,funded by National Science Foundation,Department of Defense,NIST,New Jersey Science and Technology Commission, and industry.He was the recipient of NSFs Research Initiation Award, CIM University-LEAD Award by Society of Manufacturing Engineers,Perlis Research Award and Fenster Innovation in Engineering Education Award by NJIT,Humboldt Research Award for US Senior Scientists,Leadership Award and Academic Achievement Award by Chinese Association for Science and Technology-USA,Asian American Achievement Award by Asian American Heritage Council of New Jersey,and Outstanding Contributions Award, Distinguished Lecturership and Franklin V.Taylor Memorial Award of IEEE SMC Society,and Distinguished Service Award from IEEE Robotics and Automation Society.He is founding Co-chair of Enterprise Information Systems Technical Committee(TC)and Environmental Sensing,Networking, and Decision-making TC of IEEE SMC Society.He has been among most highly cited scholars for years and ranked top one in the field of engineering worldwide in 2012 by Web of Science/Thomson Reuters.He is Fellow International Federation of Automatic Control(IFAC)and American Association for the Advancement of Science(AAAS).Corresponding author of this paper.

Dan You received the bachelor degree from the School of Information and Electronic Engineering, Zhejiang Gongshang University,China,in 2014. She is currently a master student at the School of Information and Electronic Engineering,Zhejiang Gongshang University.Her research interests include supervisory control of discrete event systems,and Petri net theory and application.
I.INTRODUCTION
t
June 5,2015;accepted July 27,2015.This work was supported by National Natural Science Foundation of China (61374148,61472361,61374005),Natural Science Foundation of Zhejiang Province(LY15F030003,LY15F030002,LR14F020001),the National Science Foundation of USA(CMMI-1162482),the Opening Project of State Key Laboratory for Manufacturing Systems Engineering(sklms2014011),Zhejiang NNST Key Laboratory(2015C31064),and the State Scholarship Fund of China.Recommended by Associate Editor Fei-Yue Wang.
:Shouguang Wang,Mengdi Gan,Mengchu Zhou,Dan You.A reduced reachability tree for a class of unbounded Petri nets.IEEE/CAA Journal of Automatica Sinica,2015,2(4):345-352
Index Terms—Petri nets,reachability tree,deadlock.
P ETRI nets[1-11]have been widely used for modeling and control of discrete event system(DES)since 1960s.As a well-known analysis tool of Petri nets,reachability trees, i.e.,the tree representations of their reachability sets,are fundamental and powerful for checking various properties such as reachability,boundedness,liveness,reversibility and coverability[12-19].However,such a tree may be an infinite tree for a given initial state or marking[7].In past decades, many scholars focused on finding a finite representation for an infinite reachability tree.
猜你喜欢
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Logic-based Reset Adaptation Design for Improving Transient Performance of Nonlinear Systems
- Security Risk Assessment of Cyber Physical Power System Based on Rough Set and Gene Expression Programming
- Security-aware Signal Packing Algorithm for CAN-based Automotive Cyber-physical Systems
- A Priority-aware Frequency Domain Polling MAC Protocol for OFDMA-based Networks in Cyber-physical Systems
- Review Expert Collaborative Recommendation Algorithm Based on Topic Relationship
- Function Observer Based Event-triggered Control for Linear Systems with Guaranteed L∞-Gain
