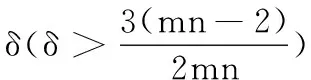Rn+m中极小子流形的刚性定理

韩英波, 李 静, 方联银

(信阳师范学院 数学与信息科学学院, 河南 信阳 464000)

0 引言

设Mn是Rn+m中一个n维完备极小浸入子流形.当m=1时,M称作稳定的,如果

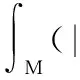
对于数δ≥0,M称作δ稳定的,如果

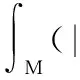
当具有更高余维数时,Spruck[7]得到:对于一个变分向量场E=fυ来说,Vol(Mt)的第二变分满足:

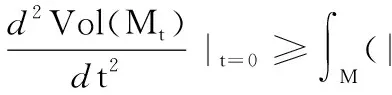
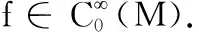
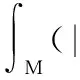
当m=1时,超稳定的定义与稳定的定义相同.

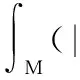
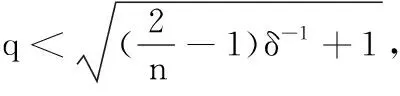
那么M是仿射平面.

本文研究Rn+m中不具有平坦法丛的完备δ超稳定极小子流形,得到结果定理1.

1 预备知识

任意ν∈Γ(NM),形状算子Aν:TM→TM满足:

〈BXY,ν〉=〈Aν(X),Y〉.

子流形的第二基本形式及曲率张量、法丛的曲率张量及外围流形的曲率张量满足下面的Gauss方程、Codazzi方程以及Ricci方程.

〈BXZ,BYW〉,

〈BXei,ν〉〈BYei,μ〉,

其中：{ei}为M的一组局部正交标架场;X,Y,Z为切向量;μ,ν为M的法向量场.在这里以及随后的运算中我们采用求和公约,并约定下列指标范围:

1≤i,j≤n; 1≤α,β≤m.

考虑(m+n)-维欧式空间Rn+m(m≥2)中的n维极小子流形Mn,有下面结论(见[12])

回忆记号:B=B∘Bt∘B,其中Bt为B的共轭映射;

当余维数m=1时,它是最优估计.当m≥2,文献[13-14]给出精确估计如下:

把上式代入式(4)得:

因此得出结论:

(6)

引理1[15]

(7)

由不等式(6)和(7)得:

(8)

2 定理及证明

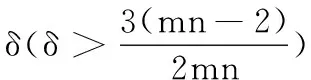
(a) 如果

(b) 如果

那么M是一个仿射平面.

△u=u(△logu+|logu|2)=

其中第一个不等式利用了式(8).由式(11)可得:

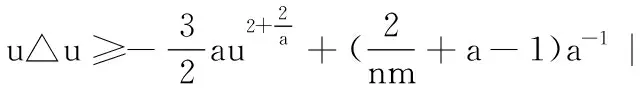
(12)

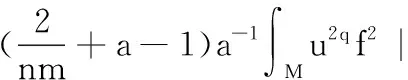
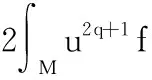
(13)

由式(13),可得

(14)

利用Cauchy-Schwarz不等式,得到:

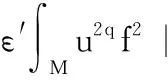
(15)

由式(14)和(15),可得:

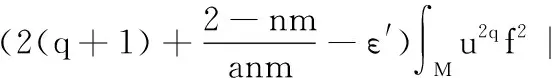
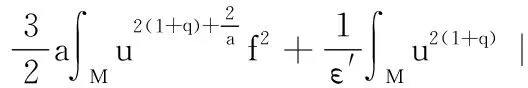
(16)

另一方面,式(1)中用uq+1f替代f,得到:

(17)

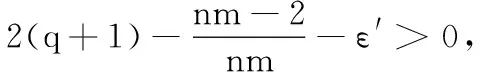
(18)

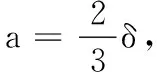
选取充分小的ε′>0,使得

(1+q)(1+q+ε′)δ>0,

令ε→0.由式(18)可得:

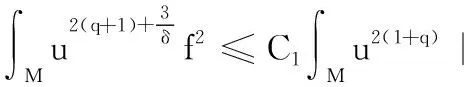
(19)

其中

u2+2q|

利用β的任意性,取β充分小,使得下式成立

由式(19)和(20),可得:

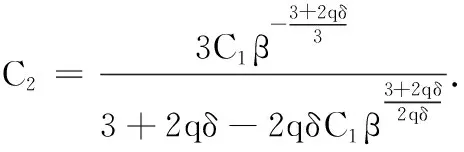
其中

对任意固定的R>0,取一个光滑函数f(r),它满足

其中C0是一个正的常数.由式(22)可得

令R→,由假设

以及式(23)可得B=0,即M是仿射平面.

选取充分小的ε′,使得

令ε→0,由式(18)可得:

(25)

其中C4是依赖于n,m,ε′的常数.

3 结论