耦合(gR,eR,gw)空间中粒子产生的动力学普适性
2015-08-09赵树松
赵 喜,赵树松
(1.云南师范大学 商学院,云南 昆明 650106;2.云南大学 物理科学技术学院,云南 昆明 650091)
0 引言
亚群对称性(Bose场与Fermi场)获得大量实验证据后,确定出量子场反常维度的实验值-γB(gR)≌1/16,这种N-强子产生的力学对称群得到重视[1-2].“Intermittency”效应的实验发现和精测量(1993—1997)[3],数据都呈四动量差Q的幂律,幂指数恰恰是γB(gR) 的整数倍[4-5].量子场反常维度γB(gR) 成为不可缺少的物理量[6-7],光子、μ-子与中微子Vμ的动量分布实验结果与强子的相似性被发现后,亚群无穷小算子和γBF(gR),γBF(eR)与γBF(gW) 之间的关系成为必要的研究内容.
1 量子场的亚群与半群对称性
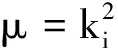

亚群无穷小算符D表达的截面格林函数对称性(不变性)是一个方程:
(1)
这里:NBFγBF(gR)=NBγB(gR)+NFγF(gR),N=NB+NF,算符D的表达式为:
(2)
这里:γm(gR)是质量反常维度,β(gR)为Callan-Symanzik函数.亚群不变性方程(2) 与重整化群的Callan-Symanzik方程数学结构相同,式(2)又可为亚群Callan-Symanzik方程.用亚群符号将两种Callan-Symanzik方程在(gR,∂r,gW)空间的形状写为类似式(2)中算符D的方式:
(3)
或方程(1)的形状:
(4)

2 粲介子D→μvμ实验与光子实验



图产生的中微子横动量分布

图产生光子的横动量分布
π±介子横动量分布由Basset广函(aQ⊥)-VKV(aQ⊥)描写:
(5)
这里指标ν中包含量子场反常维度:
(6)
(7)
为方便计,将式(7)写成式(6)形状:
(8)
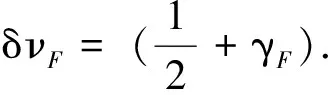
(9)
(10)
其中,式(9)对应Bose粒子,式(10)对应Fermi粒子.Basset广函式(5)在图1与图2中用实线表示,式(9)和式(10)分别确定曲线斜率为零的x⊥值,由实验数据能定出γB(gR,eR)与γF(gR,eR)的实验值.
3 结论与讨论
在式(6)与式(7)中的γB(gR,eR)与γF(gR,eR)是量子场的Hausdorff维度,反映量子场的拓扑不变性.对于光子与中微子,γBF是(eR,gW)耦合面中的反常维度,耦合面上存在Weinberg-Salam关系:
eR=gWsinθW,
(11)
其中,sin2θW=0.224 5±0.000 6.
中微子是弱相互作用粒子,因此其动量分布参数为:
(12)

光子是量子电动力学(QED)中的Bose子,其Hausdorff维度为γB(eR),动量分布参数为:
(13)
这里QED微扰论的结果为:γB(eR)=2ae/3π(ae=1/137),式(13)在误差范围内与实验数据符合(图2).
在耦合(gR,eR,gW)空间中π±介子的Hausdorff维度应写为γB(gR,eR,0),光子为γB(0,eR,0),中微子为γB(0,0,gW),于是亚群无穷小算符的形状为:
(14)
这里的β函数既是γ光子与中微子实验的要求,也与式(11)相容,而式(3)与(4)的算符D不适合N-强子产生过程和γ,νμ产生的动力学.
综上所述,利用Basset广函对中微子和光子的横动量实验数据分布进行拟合,拟合结果证明Basset广函(aQ⊥)-VKV(aQ⊥)理论的正确性,并由此得出亚群无穷小算符的形状,利用此算符,今后将在强子喷注、质量效应、动力学奇异性等方面进行更进一步的工作.
