Job-shop调度问题的离散布谷鸟搜索算法求解
2015-08-09储泽楠王庆喜
储泽楠,王庆喜
(安阳工学院 计算机科学与信息工程学院, 河南 安阳 455000)
0 引言
作业车间调度问题(Job-shop scheduling problem, JSP)是一类满足任务配置和顺序约束要求的资源分配的调度问题,具有广泛的应用背景,譬如生产制造、交通规划、邮电通信、大规模集成电路设计等问题.JSP已被证明是一个典型的NP-hard问题[1],它的求解难度远大于流水线调度问题,针对其算法的研究一直是学术界和工程界共同关注的重要课题.
目前,制造业的竞争日益激烈,制造企业正朝着有不同完工时间和产品要求的多类型、小批量的生产模式发展.如何利用现有的资源,满足加工任务所需的各种约束,使所有的任务能尽量按时完成,即如何有效地解决JSP问题,就成为一个十分现实和迫切的问题[2].
1 Job-shop调度问题描述
Job-shop调度问题描述为:n个工件在m台机器上加工,Oij表示第i个工件在第j台机器上的操作,相应的操作时间Tij为已知,事先给定各工件在各机器上的加工次序,要求确定与技术约束条件相容的各机器上所有工件的加工次序,使加工性能指标达到最优.在Job-shop问题中,通常假定每一时刻每台机器只能加工一个工件,且每个工件只能被一台机器所加工,同时加工过程为不间断,机器间缓冲区容量为无限.Job-shop调度问题是一类典型的加工调度问题,是许多实际问题的简化模型[2].
关于JSP的求解往往要考虑生产调度实际期望达到的优化指标,问题的目标函数是这些优化指标的抽象表示,JSP模型的目标函数随着企业所重点考虑因素的不同而改变.通常JSP所考虑的优化目标有3种[3]:任务的最大完工时间最短、任务的总的拖期最短和任务的提前/拖期惩罚代价最小.本文所考虑的优化目标是任务的最大完工时间最短,即完成所有任务所需的时间最短,对该指标的优化有利于提高单位时间内设备的利用率,从而提高生产的实际效率.
常见的作业车间调度问题基本数学模型有3种:整数规划模型、线性规划模型和析取图模型.本文采用Bake[4]给出的JSP整数规划模型,其调度问题可描述为:
(1)
Subject to:
Cik-pik+M(1-aihk)≥Cih,
(2)
Cjk-Cik+M(1-xijk)≥pjk,
(3)
Cik≥0,
(4)
xijk=0或1.
(5)
其中:i,j=1,2,…,n;h,k=1,2,…,m.
式(1)表示目标函数,式(2)表示工艺约束条件决定的每个工件的操作先后顺序,式(3)表示加工每个工件的每台机器的先后顺序.式(3)和式(4)中的Cik和pik分别为工件i在机器k上的完成时间和加工时间,M是一个足够大的正数,aihk和xijk分别为指示系数和指示变量,其含义为:
(6)
(7)
2 布谷鸟搜索算法
2.1 算法仿生原理
在自然界中,布谷鸟通过巢寄生的行为方式进行繁育,巢寄生是指鸟类将卵产在其他鸟的鸟巢中,由其他鸟代为孵化和育雏的一种特殊的繁殖行为[5].在宿主的选择上,布谷鸟在繁殖期寻找与孵化期和育雏期相似、雏鸟食性基本相同、卵形与颜色易仿的宿主,多为雀形目鸟类.而且它每飞到一个巢窝里只产一个卵,布谷鸟在产卵前常把宿主一枚卵移走,或全部推出巢外,迫使宿主重新产卵,来增加其卵被孵化的概率.为了繁衍宿主鸟也进化出一套反寄生行为,宿主一旦识别出寄生卵,就将其扔出或弃巢,在其他地方另建新巢.巢寄生的协同进化表现在长期的适应选择中,寄生卵的大小、颜色、卵斑等特征都与其特定的宿主相似,这有利于降低其卵被抛弃的可能性并因此增加其繁殖率.
研究表明,很多动物和昆虫的飞行行为表现出莱维飞行的典型特征[6].莱维飞行属于随机行走的一种,在莱维飞行中步长分布满足一个重尾的稳定分布,在这种形式的行走中,短距离的探索与偶尔较长距离的行走相间.目前莱维飞行行为已被用于优化和最优搜索领域,具有扩大搜索范围、增加种群多样性、易跳出局部最优点等特征[7].
2.2 算法的数学描述与分析
为了便于描述布谷鸟算法,本算法基于以下三个理想化的规则[8]:
1)每只布谷鸟一次产一个卵,并把它的卵产在随机选择的巢中进行孵化;
2)带有优质卵(或解决方案)的最优鸟巢将会保留到下一代;
3)宿主鸟巢数量固定,宿主发现外来卵的概率为pa,在宿主识别出寄生卵的情况下,宿主可能将其扔出或弃巢,并在其他地方另建新巢.为了简单起见,假定pa为一个固定值.
用CS算法在多维空间寻找最优解,对于最大化问题,解决方案的质量或适应值可以简单地与目标函数值成比例,在本算法中其他形式的适应值可以使用类似于遗传算法中适应函数的方式进行定义.为了简单起见,我们可以使用下面的简单陈述即一个巢里的每个蛋代表一种解决方案,以及一个布谷鸟蛋代表了一种新的解决方案,目的是利用新的以及潜在更好的解决方案(布谷鸟)取代巢里一个不那么好的解决方案[9].
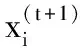
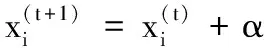
(8)
其中,α>0为步长大小,与所研究问题的范围有关.在大多数情况下,取α=1.式(8)本质上是随机行走的一个随机方程,一般情况下,一个随机行走是一个马尔科夫链,其下一个状态或位置只取决于当前的位置(上述方程的第一项)和转移概率(第二项).⊕为点对点乘法,这与PSO算法相似.但是本算法中通过莱维飞行的随机行走能够更有效地探索搜索空间,因为从长远来看它的步长更长.
莱维飞行本质上提供了一个随机行走,而随机步长来自Levy分布:
L=t-λ(1<λ≤3).
(9)
该分布有一个无穷方差和无穷均值.其步长本质上构成一个随机行走过程.其中一些新解应该由莱维行走在目前所获得最优解附近产生,这将加快局部搜索速度.然而相当部分的最优解应该由远场随机搜索产生,其位置应离当前最优解足够远,这将确保系统不会陷入局部最优.
2.3 算法流程
综上所述,布谷鸟算法流程如下:
1)设置算法参数;
2)目标函数f(x),x=(x1,x2,…,xd)T,随机产生n个鸟窝的初始位置xi(i=1,2,…,n),进行初始化;
3)计算每个鸟窝的目标函数值,并记录当前最优鸟窝位置(解决方案);
4)保留上代最优鸟窝位置,并按位置更新公式(1)对其他鸟窝位置进行更新;
5)对每一鸟窝按条件更新位置:用一个随机数pa作为鸟窝主人发现外来鸟蛋的可能性并与p0进行比较,若pa>p0,则随机改变鸟窝位置.否则,保持原来位置,得到一组新的鸟窝位置;
6)将现有鸟窝位置与上一代鸟窝位置进行对比,若较好,则将其作为当前的最好位置;
7)如若未满足结束条件,则返回3;
8)输出全局最优位置.
3 离散布谷鸟搜索算法
3.1 算法思想
原始布谷鸟算法只能解决连续性问题,对于JSP这类离散型的组合优化问题无能为力,因为布谷鸟初始化位置以及更新后的位置数据都是一个范围内的实数,而JSP问题的数据是表示加工顺序的序列值以及加工时间.因此本文为了处理离散型问题,求解JSP,把鸟窝位置的数据进行编码,编码成JSP问题中的加工顺序.
3.2 编码方式
Job-shop调度问题最常用的编码方式是直接采用工件的排序.由于CS算法中鸟窝位置为连续值矢量,标准CS算法无法实现工件排序的更新,因此构造从鸟窝位置到工件排序的恰当映射是应用CS算法解决JSP的首要和关键问题.利用编码完善后的布谷鸟搜索算法(CS)本文称为离散布谷鸟搜索算法(DCS).
虽然鸟窝位置矢量xi=[xi,1,xi,2,…,xi,n]本身无法表示加工工件的排序,但基于升序排列(Ranked Order Value, ROV)规则可以利用各个位置分量值的大小次序关系,结合随机键进行编码,将鸟窝的连续位置xi=[xi,1,xi,2,…,xi,n]转换为机器上各工件的离散的加工工序π=[j1,j2,…,jn],从而计算出鸟窝所对应调度方案的目标值.通过这种转化,无须修改CS算法的进化操作,并能够保证调度方案的可行性.
ROV规则的具体描述如下:对于一个鸟窝位置矢量,首先将值最小的分量位置赋予ROV值1,其次将值第二小的分量位置赋予ROV值2,依此类推,最终所有分量位置都会被赋予唯一的一个ROV值,继而根据ROV值就可产生一个工件排序.在表1中用一个简单的例子来说明ROV规则的工作原理和过程.

表1 鸟窝位置及其对应的ROV值
例如考虑5个工件的置换流水线调度问题,鸟窝位置为5维矢量,假设位置矢量为xi=[0.06,2.99,1.86,3.73,0.67],则首先赋予最小分量位置xi,1的ROV值为1,接下来赋予xi,5对应的分量位置ROV值为2,然后分别赋予xi,3,xi,2和xi,4对应的分量位置ROV值为3、4、5,从而得到工件的加工次序,即π=[1,4,3,5,2].
3.3 求解JSP步骤
DCS算法的实施过程与步骤如下:
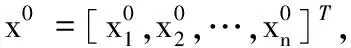

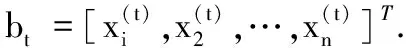

4 仿真实验
鉴于JSP的重要性和代表性,许多研究工作者设计了若干典型问题(benchmarks),用以测试和比较不同方法的优化性能,典型的Job-shop调度问题有FT类、LA类、ABZ类、ORB类、SWV类、YN类、TD类和DMU类等,其中以FT类、LA类和TD类调度问题的研究居多.LA类问题由Lawrence(1984)给出,包括40个典型问题,命名为LA1-LA40,对应8个不同规模(每一规模包含5个问题),分别为10×5、15×5、20×5、10×10、15×10、20×10、30×10、15×15.为了便于比较并验证布谷鸟搜索算法(CS)求解JSP的性能,本研究选取LA1~LA20基准问题作为算例进行仿真测试,并与基本粒子群算法(Basic particle swarm optimization, BPSO)和萤火虫算法(Firefly Algorithm, FA)所得结果进行比较.
实验仿真环境为:操作系统Windows XP,CPU Intel G630 2.7 GH和内存2 G,采用仿真软件matlab7.8实现算法编程.算法参数设置如下:布谷鸟搜索算法中,鸟巢个数n=30,宿主鸟发现外来鸟蛋的概率pa=0.25;萤火虫算法中,萤火虫数n=30,光强吸引系数γ=1.0,最大吸引度β0=1.0,步长因子α=0.2;基本n粒子群算法中,粒子数n=30,学习因子c1=0.8,c2=1.2,惯性权重w=0.5.最大迭代次数均为1000,每种算法均独立运行50次,测试结果如表2所示.
5 结语
本文对布谷鸟搜索算法的优化机理进行了分析,并使用离散编码方式完善原始布谷鸟算法,提出离散布谷鸟算法,使布谷鸟搜索算法能够解决离散型问题.该算法是基于自然界中布谷鸟种类的巢寄生行为,并结合莱维飞行提高算法的全局搜索效率,可用于解决各种复杂优化问题.该算法具有算法参数少,以及很好把握了局部搜索和全局搜索之间的平衡等优点.通过将离散布谷鸟搜索算法用于置换流水车间调度问题的研究,并与FA和PSO算法进行比较研究,显示出了DCS算法的有效性、快速收敛性和较强鲁棒性,表明了DCS算法在解决离散空间优化问题的可行性和有效性,具有良好的应用前景.

表2 PSO、FA和CS算法比较结果
注: c为问题已知最优值;min为算法50次仿真得到的最小完工时间;max为最大完工时间;avg平均完工时间;std完工时间标准方差(其中avg、std为四舍五入后所得结果).
