三维饱和地基人工黏弹性边界

马怀发，杨茹

（1.中国水利水电科学研究院流域水循环模拟与调控国家重点实验室，北京100038；2.中国水利水电科学研究院工程抗震中心，北京100048）

三维饱和地基人工黏弹性边界

马怀发1，2，杨茹2

（1.中国水利水电科学研究院流域水循环模拟与调控国家重点实验室，北京100038；2.中国水利水电科学研究院工程抗震中心，北京100048）

本文针对中低频率工程振动问题，不计流体加速度，基于球面波动方程导出了无限大三维饱和地基人工黏弹性边界及其流量边界条件。在此基础上给出了具有人工黏弹性边界的饱和土体动力固结问题虚位移原理。根据有限元语言编写出算法脚本文件，并基于有限元自动生成系统（FEPG），生成了计算源代码程序。通过在无限大地基表面施加冲击荷载和突加荷载的数值算例，验证了所建立方程和程序的正确性。本文方法可以应用于三维饱和地基的动力固结问题数值模拟。

半无限饱和地基；三维人工黏弹性边界；虚位移原理；孔隙水压力；有效应力

1 研究背景

根据地震的传播机制，地震荷载是从远域地基波及到土体结构，而后产生地震响应。地震波由远及近，再由近及远传播。在采用有限元法进行动力分析时，一般将半无限地基划分为邻近结构的近域地基和其外围的远域地基。近域地基及土体结构构成了地震响应分析的研究对象，而切割近域和远域地基的边界即形成了人工边界。人工边界分为全局边界和局部边界，全局边界虽然是对无限介质的精确模拟，但其时空偶联的频域求解方法难以在有限元中实现，非线性问题不好考虑。局部人工边界是时空解耦的，并且易于实现、计算量小，因而得到了广泛的研究和应用。目前，用的比较多的是人工透射边界［1］、黏性边界［2］和在黏性边界基础上发展的黏弹性边界［3-7］。黏性边界因其概念清楚、易于应用的特点，一度得到了广泛的研究和应用，但其存在低频稳定性问题，而且从一维推广到多维有很大的误差。黏弹性边界是在黏性边界的基础上增加了弹簧，即通过沿人工边界设置一系列线性弹簧和阻尼器组成的简单力学模型来吸收射向人工边界的波动能量，从而达到消除反射的效果，并能模拟地基的弹性恢复能力，可以很好地模拟波动在无限地基中的真实传播过程。Deeks［3］基于柱面波给出了二维黏弹性人工边界的应力公式，刘晶波［5-6］等人基于球面波推导了三维黏弹性人工边界，并给出了边界的等效刚度和阻尼系数，马怀发等［7］在分析黏弹性边界方法的理论基础上建立了统一的虚位移方程，郝明辉［8］等将其应用于拱坝计算。

强震作用下土坝、土体边坡及其地基会产生液化失稳问题，因此对其进行抗震安全评价理应将土体看作由土骨架和孔隙水两相材料组成。动力分析不仅要给出土骨架的位移时程还要计算出孔隙水压力的变化时程。与单向固体结构的人工黏弹性边界［3-7］不同，对于饱和土体的人工边界，除了要处理位移边界条件外，还要考虑孔隙水压力在人工边界的传播。Modaressi等［9］基于简化的比奥（Biot）方程，针对实际土木工程的中低频率振动并且渗透系数比较小的情况，忽略第二类压缩波，将傍轴近似应用于两相介质，提出了饱和介质动力方程u-p形式的黏性边界。Akiyoshi等［10］进一步给出了u-w和u-U形式的饱和介质时域黏性边界。王子辉等［11］基于u-U形式分别给出了具有辐射阻尼性质的外行柱面波和球面波在圆柱面和球面人工边界上引起的法向、切向应力的表达式，同时模拟了二维半空间无限域介质的能量吸收作用。刘光磊［12］基于柱面波给出了二维饱和地基u-p形式黏弹性边界条件。本文将基于比奥方程的u-p形式，研究三维饱和地基黏弹性边界条件，基于球面波给出黏弹性边界的法向和切向的弹簧系数、阻尼系数以及流量边界条件，并建立具有黏弹性边界的三维饱和地基动力学的弱解形式。

2 基本方程

2.1 动力固结方程基于比奥理论，Zienkiewicz给出了动力固结基本控制方程［13］，若规定土体中应力以受压为正，受拉为负，动力固结控制方程为：

式中：σij为饱和土的总应力；为有效应力；p为孔隙水压力；n为孔隙率；ui为土骨架位移；wi为水相对于土骨架的位移，t定 义为相对于总截面面积的平均渗流速度；εij为土骨架的应变，分别为饱和土、土和水的密度，为动力渗透系数，与土力学中渗透系数k的关系为为水的容重；λ，μ为土骨架的拉梅（Lame）常数α、Q为与固体和流体的压缩性相关的系数，，其中Ks、Kf和Kb分别为土颗粒、流体和土骨架的体积模量；θ为混合体体积应变；bi为重力加速度。

2.2 动力固结方程的弱形式Zienkiewicz研究表明［13］，对于包括地震工程在内的大部分中低振动频率的工程问题，中等速度运动情况下可忽略流体加速度，同时忽略土骨架相对于流体的加速度，动力固结方程变为如下形式：

将上面的动力固结控制方程写成弱解形式为

式中：Γ为应力边界，ni、nj为对应边界的方向余弦。

3 饱和地基黏弹性边界

3.1 黏弹性边界条件将结构和近场作为动力平衡系统如图1所示，由入射波产生的波动场由{} u表示，阻尼[] C和刚度[]

K反映结构和地基的动力特性。这里及下文物理量下脚标“b”表示人工边界，“s”表示结构。假定该系统中一散射波源以球面波动的形式向人工边界传播，基于球面波理论建立黏弹性边界条件。设球坐标系为（r，φ，θ），波动问题可视为球对称问题，因此所有力学变量只和r有关，分析问题时可只考虑径向r和垂直于径向的两个切线方向φ和θ。由于问题的对称性，位移：应变：；应力，式中：ur为径向位移，εr为径向正应变，εθ和εϕ为切向正应变，σr为球面的径向正应力，σθ和 σϕ为切向正应力。几何方程：

可忽略流体加速度和土骨架加速度后，在球坐标下将式（2）两边同时对r求导得：

图1 结构-地基动力平衡系统

再将（4）式两边同时对t求导，并代入式（7）可得球坐标系下孔压和位移的关系式：

当渗透系数比较小时，可假设渗透系数k=0，因此kf=0。研究表明，当渗透系数比较小时，此假设所引起的误差可以忽略［13-14］。则式（8）可表示为：

由此可导出用位移表示的波动方程：

令

式中：Vp为膨胀玻（P波）在饱和介质中的传播速度。引入位移势函数

式（10）可表示为：

则方程（13）的解为：

球面波阵面上法向应力和位移满足：

在?黏弹性人工边界的物理模型中［5］，黏弹性人工边界节点上的应力与位移满足的微分方程：

对比式（15）和式（16）可得黏弹性人工边界法向应力边界条件

孔压只对法向应力有影响，剪切方向有效应力与总应力相等，则剪切应力与位移满足微分方程：

式中Vs为饱和介质中剪切波波速，

由式（18）可得黏弹性人工边界切向应力边界条件

由以上参数可以发现，三维饱和地基黏弹性边界的参数形式和一般的三维黏弹性边界的参数形式一样，不同的是波速考虑了孔隙水的影响。

3.2 黏弹性边界流量假设动力计算过程饱和土体的渗流符合达西定律，流量边界条件为：

将式（9）代入得：

将位移势函数式（12）代入得边界法向流量表达式为：

可以看出，虽然二维和三维的控制方程形式不同，波动理论也不同，但是边界流量公式的形式［12］最终是相同的。

4 人工黏弹性边界的虚位移原理

4.1 方程的弱解形式根据文献［7］给出的单相体结构的黏弹性边界虚位移原理，当求解的数值模型采用人工黏弹性边界时，三维饱和地基动力固结控制方程及其边界条件可以写成如下统一的形式：

式中：Fˉmb作用在人工边界上地震波动转化荷载；为黏弹性人工边界上的等效刚度系数；为黏弹性人工边界上的等效阻尼系数；Svs为黏弹性边界，假定散射源到人工边界的距离rb可近似地取表面中心到人工边界的距离。上角标：m=±x，±y，-z；下脚标：i，j，k=1，2，3。其中，

这里，αN和αT取值范围［15］分别为1～2.0和0.5～1。本文αN和αT分别取1.2、0.5。

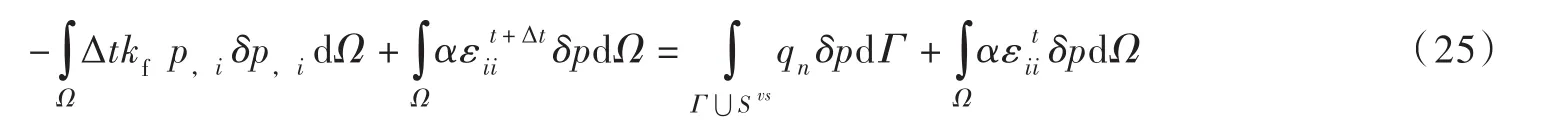
εt

方程（26）是动力固结方程（5）在引入人工黏弹性边界后的积分弱解形式。

4.2 算法及FEPG脚本文件利用方程（26）可建立其有限元数值离散模型，联立求解土骨架变形和孔隙水压力。关于土骨架位移ui的动力学方程是双曲线型方程，而关于孔隙水压力p的渗流方程是椭圆型方程。在常规的边界上，求解动力学方程需要给出位移边界和应力（荷载）边界条件。求解渗流方程需要给出压力边界条件。压力第二类边界条件由边界法向加速度表示流量表达式（22）给出。动力学方程中的速度、加速度采用纽马克（NEWMARK）算法进行插值离散，在空间上进行有限元离散。离散后的式（26）压力变量仅在刚度矩阵里与位移变量耦合。

本文计算程序是基于有限元程序自动生成系统（Finite Element Program Generator，FEPG）［16］开发出来的。按照该系统提供有限元语言规则［17］，根据本文提出的饱和地基人工黏弹性边界的虚位移原理式（26）编写脚本。脚本文件包括：PDE文件，FBC文件，算法（NFE，GCN和MDI）文件。体积分项由PDE表达，面积分项由FBC表达，NFE描述NEWMARK算法的广义刚度矩阵的组合关系及其算法过程，GCN文件给出求解线性方程组的求解器及时间计算流程，MDI文件给出求解未知量及PDE、FBC所对应的单元类型及高斯积分点个数。然后运行MDI命令即可生成计算源代码程序。

5 数值算例

为了验证本文给出的饱和地基黏弹性边界及其动力学虚位移方程的可靠度和准确性，将通过两个数值算例来验证。算例通过黏弹性边界结果和参考边界结果的对比验证了黏弹性边界的可靠性，并和固定边界结果对比可以看出黏弹性边界的计算结果更加合理。黏弹性边界、固定边界计算模型如图2所示，模型尺寸为48 m×48 m×24 m。土体表面为自由排水面，在表面中心8 m×8 m的区域加面荷载。计算边界采用黏弹性边界时，土体上表面自由，底面和4个侧面加黏弹性边界。固定边界计算时，土体上表面自由，前后面y向约束不透水，左右面x向约束不透水，底面z向约束不透水。参考结果是将计算区域扩大，长宽高分别变为原模型的3倍，即144 m×144 m×72 m，在计算时段内计算结果不受边界的影响，可以认为该计算结果为真实解。经计算，参考解的边界采用固定边界和黏弹性边界算出的结果是一致的，本文参考解计算采用的是黏弹性边界。

图2 饱和地基计算模型

图3 冲击荷载

计算参数与文献［10］的参数取值一致，即λ=83.3kPa；μ=125kPa；Ks=1.0×108kPa；Kf=1.0×103kPa；ρ=1.7×103kg/m3；ρf=1.0×103kg/m3；k=1.0×10-2m/s；kf=1.0×10-6m4/(N⋅s)；n=0.3；α=1.0由计算得Q=3.33 MPa，ν=0.2，E=300 kPa，Kb=166.63kPa。

计算给出内部点A（24，24，22）和黏弹性边界上点B（48，24，22）的结果，如图2模型中标注：A点位置为上表面中心正下方垂直距离为2 m处，B点为垂直黏弹性边界面对称轴上的点，与A点处于同一高度。计算发现土体在很大范围主要受自由表面和荷载的影响，因此内部取最具代表性的点A。B为黏弹性边界对称轴上的点，竖向位移最大且具有不为零孔压。

5.1 冲击荷载计算模型的面荷载为冲击荷载，荷载形式为半周期正弦波（周期为0.4s），峰值为1000 Pa即P=1000sinωt，如图3所示。图4和图5分别A点的孔压和竖向位移时程曲线。由图4可以看出不同的边界形式对A点的孔压值影响不大。分析原因可能是因为A点的孔压主要受表面荷载和自由表面的影响，边界对其影响很小，而竖向位移图5中可以看出，黏弹性边界的结果和参考解一致，比固定边界结果更合理。图6和图7为B点的孔压和竖向位移时程曲线。可以明显地看出，黏弹性边界的结果和参考结果基本一致，而固定边界在后面则出现出了严重的偏离。

图4 冲击荷载下A点孔压时程曲线

图5 冲击荷载下A点竖向位移时程曲线

图6 冲击荷载下B点孔压时程曲线

图7 冲击荷载下B点竖向位移时程曲线

5.2 突加荷载计算模型的面荷载为突加荷载，在0.1 s前为四分之一周期正弦波（周期为0.4 s），峰值为1 000 Pa，0.1 s后维持峰值不变，如图8所示。图9和图10分别为A点的孔压和位移时程曲线，图11和图12分别为B点的孔压和竖向位移时程曲线。从这些计算结果可以看出，突加荷载表现出了和冲击荷载结果趋势相同，黏弹性边界结果和参考结果基本一致，而固定边界结果则发生了一定程度的偏离，其中B点的响应偏离更为严重。

图8 突加荷载

本文给出两个数值算例结果虽然不同，但却表现出了相同的趋势，可以看出不同边界对A点的孔压值影响不大，是因为A点的孔压主要受表面荷载和自由表面的影响，边界对其影响很小。我们还发现，冲击荷载和突加荷载的最大值为1 000 Pa，而A点孔压的最大值都达到了1 200 Pa，出现了曼德尔效应，即上表面自由排水的饱和地基在上表面受到荷载作用时会发生固结，土中的水排出，孔压消散，但是孔压不会立即消散，而是先上升后才慢慢消散。原因是上表面在荷载作用下自由排水，土体体积收缩，体积模量增大，但是内部的水还来不及流出，上部土体对内部土体产生了束缚作用，使得孔压值有一个上升，随后才慢慢消散。而B点的孔压黏弹性边界与参考边界的结果不完全一致，主要原因可能是在计算中孔压和位移的数量级差别比较大，位移发生很小的变化，对孔压的影响都很大，而且由于在推导流量公式的过程中假设k=0，忽略了第二类压缩波的影响，而计算过程中k=0.01，采用黏弹性边界的计算结果与参考解相比具有一定误差，在文献［12］给出二维模型计算中也得到类似的结果，但这些误差在工程上是可以接受的，因此该结果适用于中砂和更小颗粒土层。

图9 突加荷载下A点孔压时程曲线

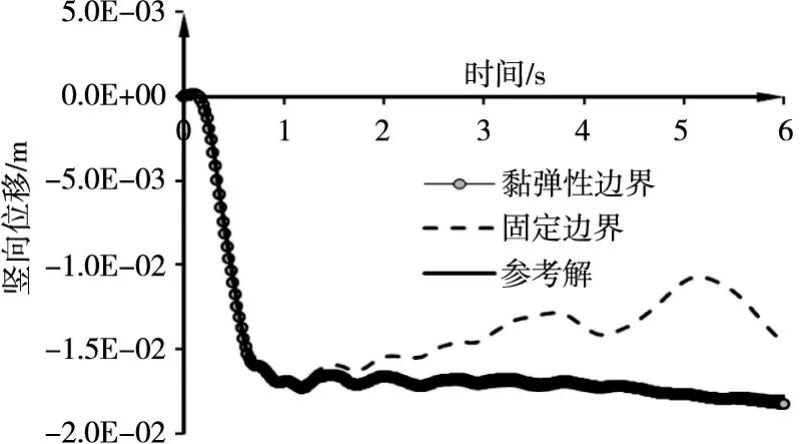
图10 突加荷载下A点竖向位移时程曲线

图11 突加荷载下B点孔压时程曲线

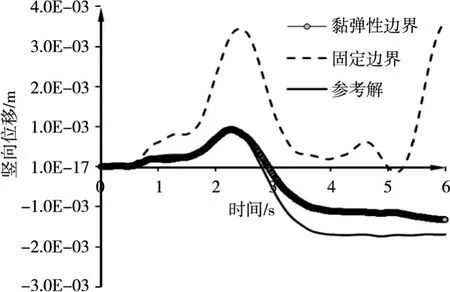
图12 突加荷载下B点竖向位移时程曲线

6 结论

本文基于球面波动方程导出了无限大三维饱和地基人工黏弹性边界及其流量边界条件。在此基础上给出了具有人工黏弹性边界的饱和土体动力固结方程一般弱解形式。然后基于FEPG有限元自动生成系统编写了脚本文件，生成了计算源代码程序。通过数值算例验证了黏弹性边界的可靠性，由计算结果和参考结果、固定边界结果的对比可以看出，黏弹性边界作为人工边界可以很好地模拟原始无限边界的阻尼效应。进一步分析发现，当渗透系数比较小时，结果更接近真实解，但是对于包括地震工程的大部分中低振动频率的工程问题，该边界可以很好地模拟中砂和更小颗粒土层的边界，也验证了所开发程序的正确性。所编写脚本文件，可以便捷的实现黏弹性边界的应用和施加，从而很方便的用于饱和地基的动力计算。

参考文献：

［1］廖振鹏.工程波动理论导论［M］.第2版.北京：科学出版社，2002：136-187.

［2］Lysmer J，Kuhlemeyer R L.Finite Dynamic Modelfor Infinite Media［J］.Journal EngineeringMethods，1969，95（EM4）：859-877.

［3］Deeks A J，Randolph M F.Axisymmetric Time-domain Transmitting Boundary［J］.Journal of Engineering Me⁃chanics，1994，120（1）：25-42.

［4］刘晶波，吕彦东.结构—地基动力相互作用问题分析的一种直接方法［J］.土木工程学报，1998，31（3）：55-64.

［5］刘晶波，王振宇，杜修力，等.波动问题中的三维时域粘弹性人工边界［J］.工程力学，2005，22（6）：46-51.

［6］刘晶波，杜义欣，闫秋实.粘弹性人工边界及地震动输入在通用有限元软件中的实现［J］.防灾减灾工程学报，2007，27：37-42.

［7］马怀发，王立涛，陈厚群.粘弹性人工边界的虚位移原理［J］.工程力学，2013，30（1）：168-174.

［8］郝明辉，张艳红，陈厚群.基于ABAQUS的黏弹性人工边界在重力坝分析中的应用［J］.中国水利水电科学研究院学报，2012，10（2）：120-126.

［9］Modaressi H，Benzenati I.An absorbing boundary element for dynamic analysis of two-phase media［C］//Earth⁃quake Engineering，Tenth Word Conference，Madrid，Spain.Rotterdam：Balkema，1992：1157-1161.

［10］Akiyoshi T，Fuchida K，Fang H L.Absorbing boundary conditions for dynamicanalysis of fluid-saturated porous media［J］.Soil Dynamics and Earthquake Engineering，1993，12：387-397.

［11］王子辉，赵成刚，董亮.流体饱和多孔介质黏弹性动力人工边界［J］.力学学报，2006，38（5）：605-611.

［12］刘光磊，宋二祥.饱和无限地基数值模拟的粘弹性传输边界［J］.岩土工程学报，2006，28（12）：2128-2133.

［13］Zienkievicz O C，Shiomi T.Dynamic behavior of saturated porous media；The generalized Biot formulation and its numerical solution［J］.International Journal for Numerical and Analytical Methods in Geomechanics，1984，8：71-96.

［14］杨军，宋二祥，陈肇元.饱和土动力反应中两类压缩波的独立作用分析［J］.岩土力学，2001，22（2）：199-203．

［15］谷音，刘晶波，杜义欣.三维一致粘弹性人工边界及等效粘弹性边界单元［J］.工程力学，2007，24（12）：31-37.

［16］梁国平，周永发.有限元语言［M］.北京：科学出版社，2013.

［17］梁国平，梁国平.有限元程序自动生成系统与有限元语言［J］.力学进展，1990，20（2）：199-204.

3D viscous-spring artificial boundaries of infinite saturated foundation

MA Huaifa1，2，YANG Ru2
（1.State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin，China Institute of Water Resources and Hydropower Research，Beijing100038，China；2.Earthquake Engineering Research Center，China Institute of Water Resources and Hydropower Research，Beijing100048，China）

Aiming at the low frequency vibration problems in engineering，regardless of fluid acceleration，the viscous-spring artificial boundary and flux boundary conditions infinite of 3D saturated ground are de⁃rivedbasedonthe spherical wave equation.Afterwards，the principle of virtual displacements of 3Dvis⁃cous-spring artificial boundary of infinite saturated foundation is proposed.Then the script files are written according to the finite element language，and based on the Finite Element ProgramGenerator（FEPG），the program source codes were generated.By means of the impact load and sudden load numerical analysis ex⁃acted on infinite ground surface，the correctness of the established equations and procedures were verified. This method can be applied to the numerical simulation of 3D saturated soil dynamic consolidation.

infinite saturated foundation；3Dviscous-spring artificial boundary；virtual displacement princi⁃ple；pore water pressure；effective stress

TU470

A

10.13244/j.cnki.jiwhr.2015.02.008

1672-3031（2015）02-0128-08

（责任编辑：韩昆）

2014-11-24

国家自然科学基金项目（51079164）；水利部公益性行业科研专项（201301057）；中国水利水电科学研究院科研专项（KJ1242）

马怀发（1962-），男，山东枣庄人，博士，教授级高级工程师，从事计算力学、水工结构抗震及混凝土细观力学分析研究。E-mail：mahf@iwhr.com

杨茹（1989-），女，陕西，硕士生，从事工程数值模拟。E-mail：yr1002151615@163.com