Numerical Reality Method of the M icroburst Model

TAO Yang(陶杨)，HAN Wei(韩维)

1 Naval Academy of Armament，Shanghai200436，China

2 Department of Airborne Vehicle Engineering，Naval Aeronautical and Astronautical University，Yantai264001，China

Numerical Reality Method of the M icroburst Model

TAO Yang(陶杨)1，2*，HAN Wei(韩维)2

1 Naval Academy of Armament，Shanghai200436，China

2 Department of Airborne Vehicle Engineering，Naval Aeronautical and Astronautical University，Yantai264001，China

An engineering m icroburst model to generate the m icroburst wind field for virtual flight simulation has been presented．Themodel is built as a finite viscosity vortex coremodel based on the vortex ring theory considering the air viscosity，and it can solve the problem of induced velocity discontinuity at the inner region near the vortex core．M oreover，the central axis velocity is obtained by turbulence free jet theory so as to avoid the singularity．The parameters in multip le-vortex-ring m icroburst model are determ ined by improved quantum genetic algorithm(QGA)based on immune and mutation operator，and the parameters optim ization of themodel under condition of differentmaximum vertical velocity are investigated．The results show that the m icroburst model is effective and accurate．The simulation results fit the preset value very well，and the error is controlled within 10－7．

microburst;vortex ring;viscosity vortex core;quantum genetic algorithm(QGA);immune and mutation operator;multiplevortex-ring model

Introduction

Themicroburst is the most dangerous form of w ind shear and severely endangers flight safety［1－2］.The m icroburst downdraft flow after impacting will spread along the ground level，and produce a horizontal outflow wind speed and a strong w ind shear near the ground.In this kind of weather phenomenon，the aircraft would encounter the headw ind component first，and cause the lift increase and the trajectory rise.Usually，pilotsmake it come back to the intended route by reducing the thrustand pitch angle，whichmay cause the aircraft energy loss.As passing through themicroburst downdraft flow，the aircraft would encounter the tailw ind component which causes the lift decrease rapidly and the normal flight altitude cannot bemaintained as well.Seriously，accidents will happen such as crash if the aircraft loses too much energy.

In current study，the engineering models of microburst are w idely used in simulation application for its simple and practical form.On the basis of JAWS statistical analysis of large amount of data，thew ind speed is considered as only a linear function of the horizontal displacement of the reference point and the linear model was given［3］.Then Woodfield and Wood［4］supposed that the w ind field obeyed the sinusoidal variation and gave the harmonic model.Neither of these two models is simple and cannot simulate the curl of the horizontal outflow.However，more accurate model of m icroburst can be built using fluid mechanics，such as vortex ring model［5－6］，vortex section model［7］，and circular doubletsheetmodel［8］.Neither of these models can simulate the m icroburst well.For example，some model neglects the vortex ring structure，some［5－7］could not simulate gas flow in the central section of the vortex ring，and some［8］is complicated and time－consum ing for real－time flight simulation.

Currently，researches on m icroburst mainly focused on single－vortex－ring models.As the vertical velocity generated from single－vortex－ring was relatively small［9］，the multiplevortex－ringmodelwas required in virtual simulation.The w ind field of certain initial multiple－vortex－ring parameters and the actually measured w ind field were compared［10－11］.If thew inds velocity varied within error range，the parameters were effective.Otherw ise，the parameters should be adjusted to calculate again.This method strongly depended on the actual data and was hard to work effectively in virtual simulation.So models to generate certain microburst w ind field with some particular characteristics，such as the maximum vertical w ind velocity，the ratio of maximum peak value between horizontal and verticalw ind velocity［9，12］，aremore prevalent.

In order to solve the shortages mentioned above，several improvements are proposed here.The microburstmodel based on vortex ring principle is researched in this paper.An integrated single－vortex－ring model is built by using velocity damping to handle singularity of vortex ring's center velocity and adopting turbulence free jet theory to get the central axis velocity.Themodel can simulate airflow in the central section well.During the process of calculating，numerical method of Simpson formula is applied to reducing the simulation time.In order to increase the using flexibility，an intelligentmethod to build the multiple－vortex－ring model is studied.The model considers the maximum vertical velocity as the optimized function，and an improved quantum genetic algorithm(QGA) based on immune and mutation operator is proposed to optimize the parameters ofmultiple－vortex－ringm icroburstmodel.

1 Single-Vortex-Ring Model

Suppose the primary vortex ring with the radius of R and the strength ofΓis placed at point Op(0，0，H)，paralleling with the ground.In order tomake the ground a stream surface，an imaginary vortex ring with the same radius and strength is placed at Om(0，0，－H)shown in Fig.1.

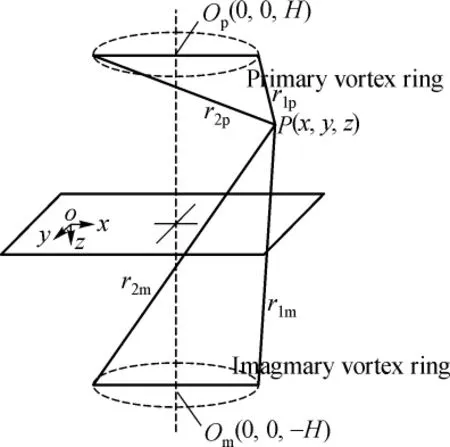
Fig.1 Single－vortex－ringmodel

Any point P(x，y，z)in space is expressed as P(r，φ，z) by the cylindrical coordinate system，whereConsidering the symmetry of the vortex ring，regardless of the azimuthal angleφ，the 3D coordinates is simplified into 2D coordinates.That is P(r，z)．The shortest distance r1pand thelongest distance r2pfrom point P to the primary vortex ring are w ritten as:

The stream function of the primary vortex ring at P is expressed［13］:

where F(λ)and E(λ)are the complete elliptic integrals of the first and the second kinds，separately.In actual calculations，the elliptic integral would cost much time.A simple solution is given which seldom affects the results［14］:

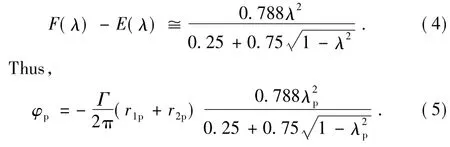
Likew ise，the shortest distance r1mand the longest distance r2mfrom point P to the imaginary vortex ring and the stream function of the imaginary vortex ring at P are:

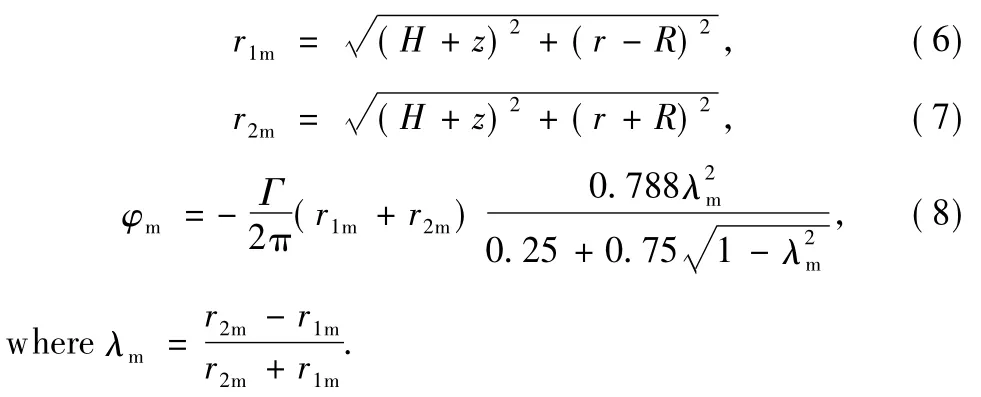
The horizontal and vertical induced velocities are described as:

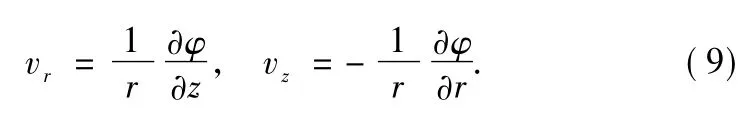
Total induced velocities are:

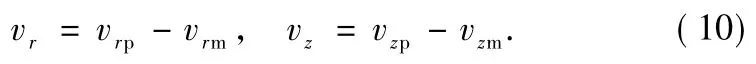
This expression is not suitable at two positions:the center of vortex core and the central axis of vortex ring.

Taking the air viscosity into account，single potential flow theory could not simulate the wind field of the m icroburst accurately.With the action of viscosity，a core with circular cross section with the radius Ra＜＜R of finite volume exists in the vortex ring.

The induced velocities calculated from Eqs.(9)－(10) would become larger as the point P approaches the center of vortex core.Finally，they would be infinity at the center.That is probably far from the truth.To conquer this problem，the vorticity is considered to be a constant，which only exists in vortex core area.Linear interpolation is used to calculate the induced velocities from the edge to the center of the vortex core［14］.The Rankine vortex model is adopted to simulate velocity distribution in the vortex core［15］.These two methods make the velocities discontinuous at the edge.To reflect reality，a viscosity vortex core model with continuous distribution of vorticity is built in this paper.

According to Refs.［9，12］，a velocity dumping coefficientξ(ξ∈［0，1］)is brought in，

The induced velocities ismodified as

Ifξ=1，itmeans that point P is far enough from the vortex core and the position is not affected by the vortex core.Ifξ=0，point P is at the center of the vortex core and the vortex core is similar to the rotating rigid body，thus，the central velocity is0. The calculation formula of Rais not given in Ref.［12］.The Hypothesis Raproportional to R［9］is lack of specific basis.For this，the radius of vortex core Rahere is treated as an individual parameter.

The horizontal velocity is0 at the central axis of the vortex ring.If Eq.(12)is used to calculate the vertical velocity，singularity may appear.The turbulence free jet theory is introduced to calculate the centralaxis velocitieswithout running into singularity.The central axis vertical velocity of the primary vortex ring isw ritten as

The central axis vertical velocity of the imaginary vortex ring is

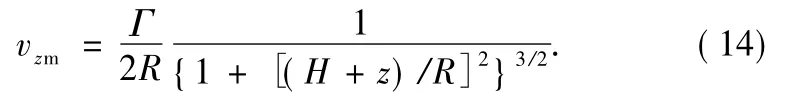
Total central axis vertical velocity is

Especially，when z=H，

So，if the central axis vertical velocity w0is given，the strength Γcan be got from Eq.(16).

2 Parameters Selection of Multiple-Vortex-Ring Model

The w ind field of multiple－vortex－ring is the superposition of independent w ind field engaged by single－vortex－ring. Supposing that the microburst is comprised of n vortex rings，the whole vertical velocity is VZ=vz，1+vz，2+…，and the maximum vertical velocity is VZmax=max(VZ)．It includes 5n－1 optimizing parameters，such as the radiiof vortex ring R，the radii of vortex core Ra，the altitudes of vortex ring H，the central axis vertical velocities w0and the horizontal deviations of centralaxis d．The objective function is f(R，Ra，H，w0，d)=where v is the presupposed maximumzmaxvertical velocity.As the value of f increases，the error between simulated results and the presupposed ones decreases.

QGA is a kind of genetic algorithm based on the principle of quantum calculation［16］.As the application fields expanding，some disadvantages emerge.For example，the arithmetic speed and computational accuracy cannot be satisfied simultaneously，and the loss of varieties causes prematurely.Consequently，the original algorithm should be improved.

The algorithm implementation is presented as follows.

Fig.2 Algorithm flow chart

(2)Calculate the appropriate length of chromosome L.

①Give a small initial length L.

②Let the objective function f be the fitness function fit().Work out the maximum fitness fitmax(x)and the minimum fitness fitmin(x)in the computational domain.

③Calculate current computational accuracyε=

④Compare it with default tolerance.Ifεis bigger，increase the length L and return to step(2).Otherw ise，L is the appropriate length of chromosome.

(3)Testand assess current population，and record the best individual and the corresponding fitness，which are the maximum vertical velocity VZbest，1and the corresponding model parameters(R，Ra，H，w0，d)best，1of the first generation. This best individual is the evolution goal of the second generation.Meanwhile，record the best5 individuals tomemory bank.

(4)Judge of the termination condition.If VZbestis very close to vzmax，quit the algorithm.Otherw ise，continue.

(5)Test and assess the population again from the second generation.Adopt elitism selection，record the best5 individuals tomemory bank and refresh thememory bank.

(6)Calculate individual's expecting reproductionprobability by immune algorithm.Let fitness function be antigen，and individuals of the population be antibody.Then the individual's expecting reproduction probability is

whereχis the immune probability constant，Avis the affinity between antigen and antibody，which is expressed by individual fitness，and Cvis the antibody consistency，

(7)Reestablish population.Eliminate the lowest 5 individuals of expecting reproduction by population catastrophe，and supply current population with the recorded high fitness individuals of the last generation.

(8)Adjust individuals by quantum revolving gate for the sake of evolving individuals.The strategy of quantum revolving gate refers to Ref.［16］.In order to strengthen the optim ization speed，the self－adopted revolving angle is used，Δθ=θmin+andθmaxare the minimum and the maximum revolving angles separately.According to the revolving angle rangeΔθ∈［0．001π，0．05π］mentioned in Ref.［17］，it is confirmed thatθminis equal to 0.001πandθmaxis equal to 0.05π.Then，record the adjusted best individual and the corresponding fitness，which are themaximum vertical velocity VZbest，iand the correspondingmodel parameters(R，Ra，H，w0，d)best，iof the i th generation.

(9)Judge whether the best individual and its fitness change or not during 5 generations.If not，enter the next step; otherw ise，go to step(11).

(10)Obtain the population of younger generation by mutation operation.The mutation process is divided into two steps.

①Change the inner structure of gene，and transform(α，β)into(β，α)．Normal single－point crossover changesmany genes of both parent chromosomes.Sometimes the excellent ones are destroyed.To avoid this，double－point crossover is used here.

②Change part of the gene sequence in each chromosome random ly.

(11)Add 1 to current generation，and turn to step(4). The algorithm flowchat is shown in Fig.2.

3 Simulation and Analysis

Supposing thata double－vortex－ringmodel is adopted here，themaximum vertical velocity VZmax=max(vz，1+vz，2)．Then use the algorithm proposed above to calculate the parameters as vzmaxis equal to 5，10，and 15m/s，separately.Set population size N=50，the maximum number of generations gen=200，the initial length of chromosome L=5，the immune probability constantχ=0.3，the threshold of immune antibody density T= 0.8，the genetic crossover probability Pc=0.95，the genetic mutation probabilitythe allowable computational accuracy tol=10－6.

In the process of calculation，while symbolic operation costs too much time，numerical method is employed.In the domain of definition，the continuous variables are dispersed by equal step.After calculating the function values of each discrete point，Simpson formula showed in Eq.(19)is used to get the derivative values.

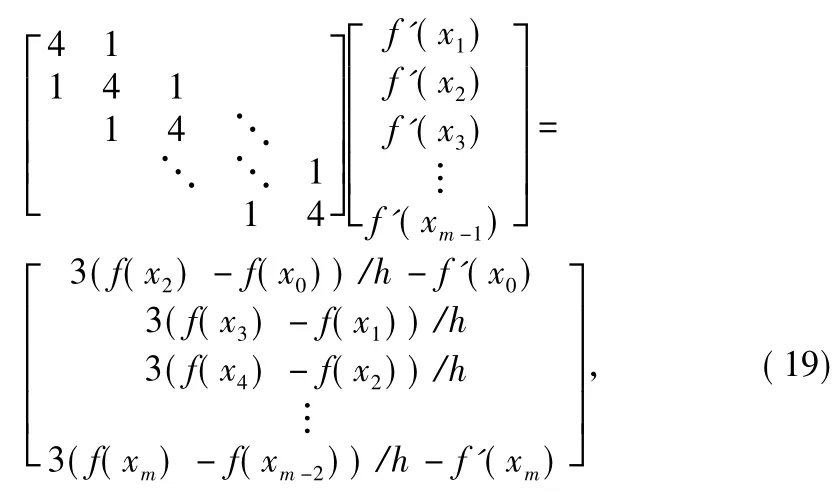
where xn=x0+mh，h is the step，derivative values of the endpoints f'(x0)and f'(xm)are calculated by the five－spot pattern.

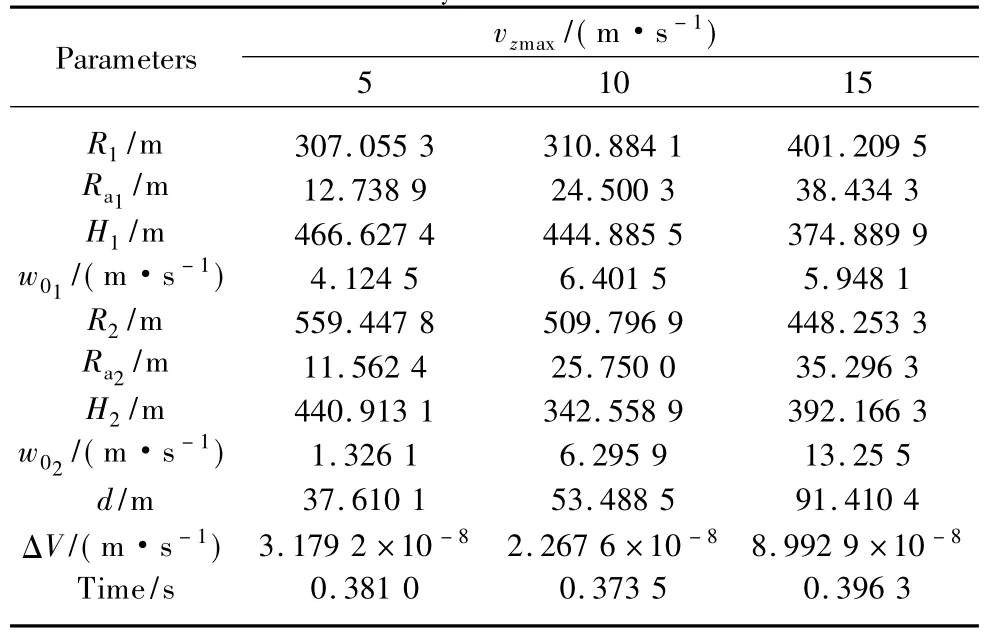
Table 1 Parameters of the double－vortex－ring model with different verticalwind velocity

As shown in Table1，the suitable parameters can be chosen with different vzmax．The radiiof vortex core Raare both at least one order of magnitude smaller than the radii of each vortex ring，and the errorΔV is two orders ofmagnitude smaller than the allowable computational accuracy tol.Thus the selection results satisfy the presupposed requestswell.Also，thismethod costs less time.

According to the parameters，when vzmaxis equal to 10 m/ s，the w ind field on symmetry plane of the two vortex rings and thew ind velocity with differentaltitudes are showed in Figs.3－5.In Fig.3，the arrow direction stands for the wind direction，and the length of arrow represents the magnitude of w ind velocity.The w ind field is composed of central high strength downdraft and ambient loop airflow.The strength of w ind field weakens away from the center.

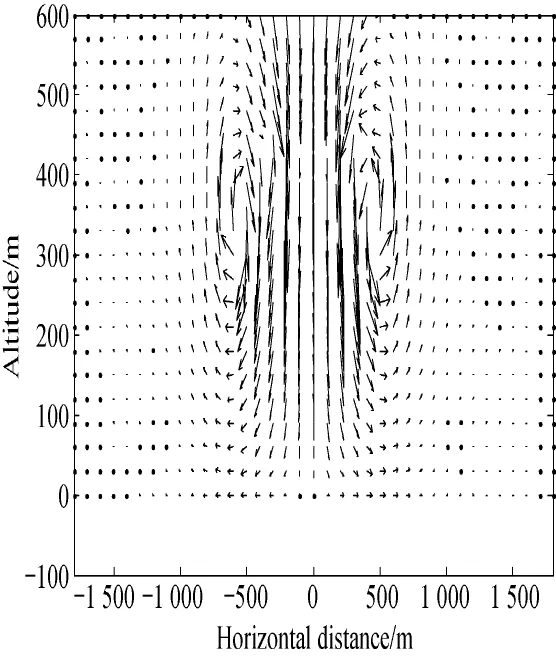
Fig.3 W ind field on the symmetry plane of the two

Because of non－coaxially of the two vortex rings，thew ind field is asymmetric in Figs.4 and 5.It is known from the characteristics of the vortex ring that the trends of airflow are opposite above and beneath the vortex ring.For a single vortex ring，the maximum vertical velocity and the minimum horizontal velocity take valuewhen h=H．The vertical velocity decreases while the horizontal velocity increases with the distance to H.As shown in Table 1，the altitudes of the two vortex rings are H1=444.885 5 m and H2=342.558 9 m，separately，and the two independent w ind field are superimposed.So if h＜H2，the vertical velocity increaseswith the decline of horizontal velocity while the altitude increases. The horizontal velocity reaches its peak near the ground.If h＞H1，the vertical velocity decreases with the raise of horizontal velocity while the altitude increases，and the direction of horizontal velocity is opposite to thatof h＜H2.If H1＜h＜H2，the direction of w ind velocity induced by the first vortex ring is opposite to the velocity induced by the second one，and the vertical velocity achieves its peak in this area.Meanwhile，the horizontal velocity which is composed of opposite induced velocity shows multi peaks and valleys shown in Fig.5.The results are the same as the distribution of real physical test in Ref.［18］.

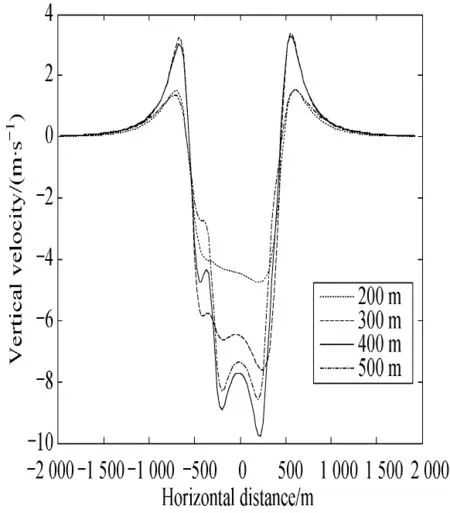
Fig.4 Vertical w ind velocity with different altitudes

Fig.5 Horizontal w ind velocity with different altitudes

4 Conclusions

The investigation on the original vortex ringmodel and the viscosity vortex ring model are presented.The original vortex ringmodel ismodified by taking into account the distribution of the vortex core under the influence of air viscosity effect.The turbulence jet theory is applied to analyzing the induced velocity distribution.Then，a complete single－vortex－ring model is established.A multiple－vortex－ringmodel is proposed for virtual experiments.Themodel sets the maximum vertical velocity as the characteristic of themicroburst，and uses an improved QGA based on immune and mutation operator to optimize the parameters of the model.Simulation results show that the methodology can flexibly construct the virtual microburst w ind field and meet the preset requirementswell.

［1］Zhou N，Liu C，Yin JH.Intelligent Control of Airplane under M icroburst W indshear［J］.Journal of Nanjing University of Aeronautics＆Astronautics，2002，34(5):479－483.(in Chinese)

［2］Dan D V.A Simple，Analytical，Axisymmetric M icroburst Model for Downdraft Estimation［R］.US:National Aeronautics and Space Adm inistration，1991.

［3］U.S.Federal Aviation Administration.W indshear Training Aid［M］.Washington，D.C.:U.S.Department of Transportation，Federal Aviation Adm inistration，Associate Adm inistrator for Development and Logistics，1987:75－79.

［4］Woodfield A A，Wood JF.Worldw ide Experience ofW ind Shear during 1981—1982［R］.US:National Aeronautics and Space Administration，1983.

［5］W ingrove R C，Bach R E.Severe W inds in the DFC M icroburst Measured from Two Aircraft［C］.AIAA 25th Aerospace Meeting，US，1987:AIAA87－2340.

［6］Nguyen H，Manuel L，Veers P.Simulation of Inflow Velocity Fields and W ind Turbine Loads during Thunderstorm Downbursts［C］.The 51st AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynam ics，and Materials Conference，US，2010: AIAA2010－2651.

［7］Liu G，Wang X R，Jia R Z.Engineering Simulation Method of Variable Wind Field in Synthetic Natural Environment［J］. Journal of System Simulation，2006，18(2):297－300.(in Chinese)

［8］Zhu S X，Etkin B.Modelof theW ind Field in a Downburst［J］. Journal of Aircraft，1985，22(7):595－601.

［9］Lin L L，Yan F，Yang JL.Use of Nested Differential Evolution Algorithm to Select M icroburst Model's Parameters［J］.Systems Engineering and Electronics，2012，34(11):2379－2383.(in Chinese)

［10］Schultz T A.Multiple－Vortex－Ring Model of the DFW M icroburst［J］.Journal of Aircraft，1990，27(2):163－168.

［11］Schultz T A.A Multiple－Vortex－Ring Model of the DFW M icroburst［C］.AIAA 26th Aerospace Sciences Meeting，US，1988:AIAA85－0685.

［12］Wu Y，Jiang S D.Parameters Selection Method of Multiple Vortex－Ring M icroburst Model Based on Nested Particle Swarm Optim ization［J］.Chinese Journal of Electronics，2012，40(1): 204－208.(in Chinese)

［13］Zhao Y.A Simplified Ring－Vortex Downburst Model［C］. AIAA 28th Aerospace Sciences Meeting，US，1990:AIAA90－0580.

［14］Ivan M.A Ring－Vortex Downburst Model for Flight Simulations［J］.Journal of Aircraft，1985，23(3):232－236.

［15］Gao Z X，Gu H B.Research on Modeling of M icroburst for Real Time FlightSimulation［J］.Journal of System Simulation，2008，20(23):6524－6528.(in Chinese)

［16］Liang C Y，Bai Hua，Cai M J，Lu W X.Advances in Quantum Genetic Algorithm［J］.Application Research of Computers，2012，29(7):2401－2405.(in Chinese)

［17］Han K H，Kim J H.On Setting the Parameters of Quantum－Inspired Evolutionary Algorithm for Practical Applications［C］. Evolutionary Computation，CEC'03，US，2003:178－184.

［18］Alahyari A，Longm ire E K.Dynam ics of Experimentally Simulated M icrobursts［J］.AIAA Journal，1995，33(11):2128－2136.

TP202.7;P425.5

A

1672－5220(2015)04－0597－05

date:2014－04－25

National Natural Science Foundation of China(No.61032001)

*Correspondence should be addressed to TAO Yang，E－mail:timothy 1205@163.com