方差分析叠加周期外推法在地震预测中的应用

2015-08-06徐清华杨林根张明哲

华南地震 2015年1期

徐清华，杨林根，张明哲

（1. 淮北市地震局，安徽淮北 235000； 2. 巢湖市地震办，安徽巢湖 238000； 3.安徽财经大学，安徽蚌埠 233000）

0 前言

某一时间序列的历史数据，包括基本模式和随机起伏，预测就是力图将基本模式从随机性变化中分解出来，用基本模式来推测未来[1]。方差分析叠加周期外推法作为统计预报实践中的一类时序周期外推法，在气象、水文、农业、地质等各方面已得到大量的应用，但在地震预测预报方面的应用尚不多见。

方差分析叠加周期外推法是一种统计分析方法[2]。它可以分析与地震活动有关因子的变化是否异常，也可以用它摸索地震本身的活动规律进行外推预报。不过，这两者都必须依附在这些因子变化的过程中确实存在有周期性变化的客观事实上。

地震是一种自然现象，一般是不可能有严格的周期。邓韫[3]认为准确地说应该叫 “拟周期或准周期”。因此，本文所讨论的的周期都是指具有某种概率的周期性。当然，如果有一些因子能够呈现周期，只是在某一时段受到其他因子的影响，其运行规律受到破坏，那么我们可以应用这种方法找出这一异常的起点，进行试验和探索[4-5]。

1 方差分析叠加周期外推法简介

1.1 基本原理

方差分析叠加周期外推法就是把某一要素序列按不同的间隔进行分组，并分别计算出不同组别下的组间方差与组内方差的比值F，通过F 大小的比较，选取出最大的F 进行某信度下的周期是否显著的检验，通过检验的可以确定在该信度下可能存在相应的周期，然后从原序列中剔除该周期的影响，在残差序列中再选下一个周期，依次类推，直至残差序列稳定（即F 检验不显著）为止，具体方法流程见图1，最后通过时间外延来预报某些要素的未来变化。

1.2 计算方法[2]

1.2.1 组间离差平方和与组内离差平方和的计算[6-7]

把n个观测数据X1， X2， ……Xn排列成表1的形式，其中： j 表示组别， j=1， 2,……b； i 为每组的项数其中， T 为总数； Tj为每组的合计数为每组的组平均值（表1）。

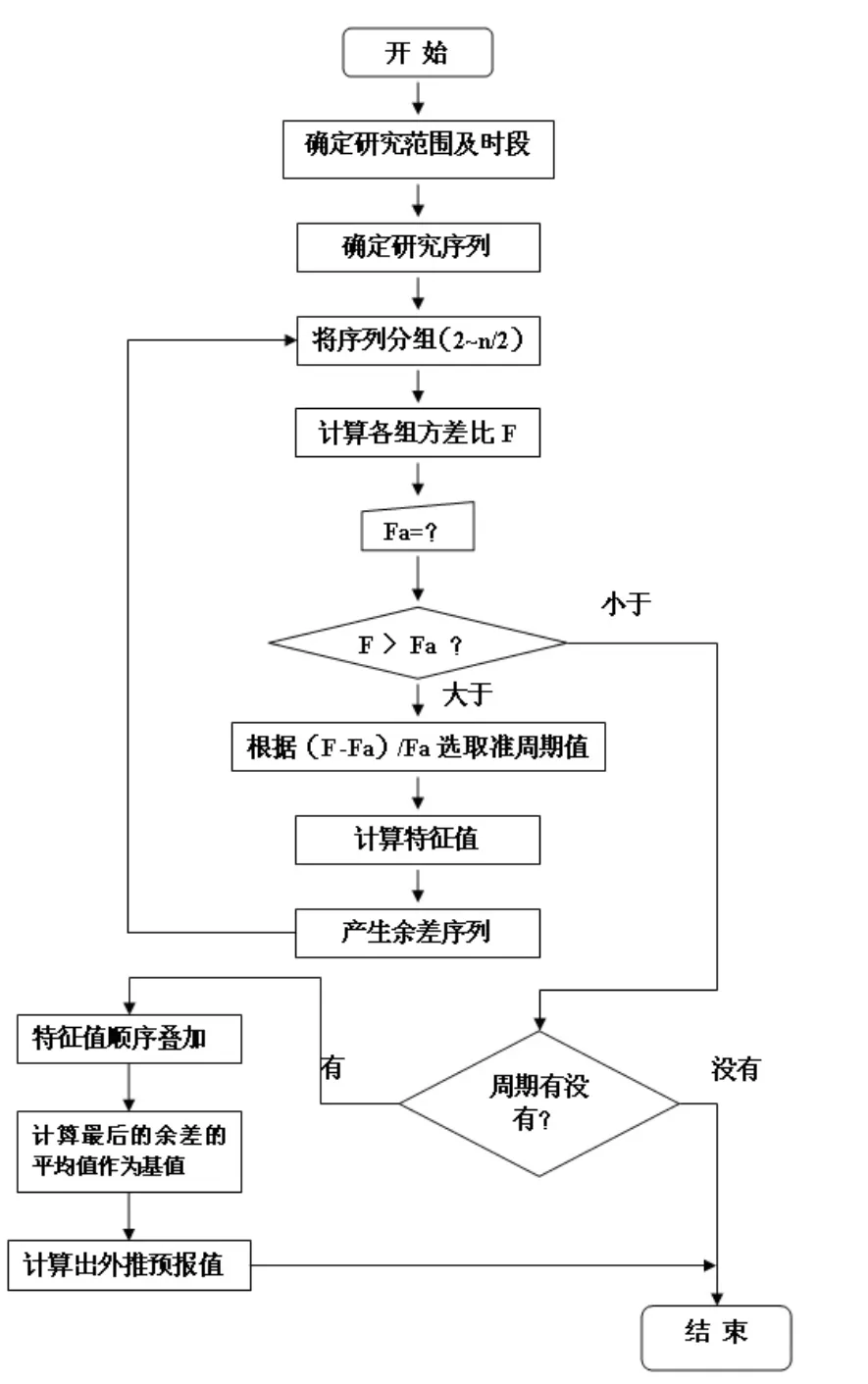
图1 方差分析叠加周期外推法的具体步骤Fig.1 Concrete steps of variance analysis superimposed by periodic extrapolation method

组间离差平方和与组内离差平方和的计算公式为：组间离差平方和组内离差平方和表示各组平均值对总平均值的离差平方和，在前面再乘以a，这是因为考虑到每组内又有a 项的关系，它表达了组与组之间数据的差异情况。组内离差平方和是指同组之内各个数据Xij对组内平均值的离差平方和，即它代表了每组内部数据的差异情况，由于共有b 组，还要把各组的相加，所以

表1 试验周期分组表Table 1 The grouped table of test cycle

1.2.2 方差比F 的确定与F 检验

由于做周期分析时，事先并不知道周期数目，因些需要从可能存在的周期中反复排列各种数值。根据方差比：

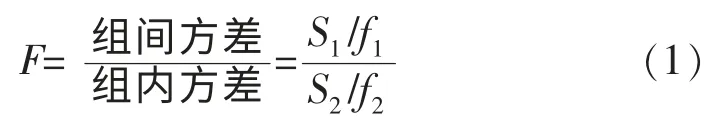
式（1）中， S1、 S2分别为组间离差平方和与组内离差平方和的； f1、 f2分别为组间离差平方和与组内离差平方和的自由度。 f1=b-1， f2＝n-b。

方差比F 在一定的条件下可以证明是一个随机变量，而且是服从F-分布的。 F-分布可以计算，也可用F-分布表查询，因此可以用F 检查的方法来检验该组周期特征是否具有显著性。

1.3 具体计算步骤

将选定区域地震的经纬度进行分组，依次取信度α=0.01、 α=0.05、 α=0.10、 α=0.20，计算各组F 值找出第一准周期，当取信度α=0.01 时，若无显著周期，则降低信度，取α=0.05，如仍无显著周期，再降低信度，取α=0.10，如也无显著周期，再取α=0.20，仍无如显著周期，则不再计算。计算第一准周期各组平均值，找出准周期各组平均值的最小值，将各组平均值减去各组平均值当中的最小值作为第一准周期的特征值，得出第一准周期特征值。

第一准周期特征值按序重复排列，将原经纬度序列对应减去第一准周期特征值，得出第一余差序列。

对第一余差序列再进行分组，计算各组周期F值，依次取信度α=0.01、 α=0.05、 α=0.10、 α=0.20，按照上面计算第一准周期的方法，计算第二准周期特征值，得出第二余差序列。

对第二余差序列再进行分组，重复上面的步骤，计算第三准周期特征值，得出第三余差序列。对第三余差序列再进行分组，重复上面的步骤，直至无显著周期。

将最后余差序列的均值作为基值，将第一准周期特征值、第二准周期特征值、第三准周期特征值等特征值叠加基值，得外推预测值。

2 实例分析

为了说明方差叠加周期外推法在地震预报中的情况，本文偿试选取不同区域、不同震级的地震进行地点外推预测。

根据地震区、地震亚区、地震带的划分方法，华北地震区分为鄂尔多斯地震亚区、冀鲁豫地震亚区。其中，冀鲁豫地震亚区又分为河北平原地震带、郯庐地震带、淮河地震带、长江中下游～南黄海地震带。郯庐地震带地震强度最高，曾发生1668年郯城8.5 级地震；河北平原地震带强度次之，最高震级8 级；淮河地震带强度最小，最大6.5 级。本文分别对这三个地震带1400年以来的5级以上地震进行方差分析，叠加周期外推，预测下一次地震可能发生的大概位置。

2.1 郯庐地震带

以郯庐断地震带为例说明方差分析叠加周期外推法的应用方法。

郯庐断裂带[9-11]是中国东部一条巨大北北东走向的断裂带，郯庐断裂带从南端的湖北广济到沈阳以北，全长1 400 km。郯庐断裂带东、西两侧的磁场特征不论是异常值的大小、规模，还是总体形态和走向均存在明显的差异。以郯庐断裂带为界，其西以北西西向走向为主，其次为北东走向；其东地区以北东走向为主，其次有北北东、北东东走向断裂。

2.1.1 郯庐地震带地震目录[12-13]

本文使用的郯庐地震带地震目录包含根据地震区、地震亚区、地震带的划分范围中的5 级以上地震。具体地震见表2、图2。

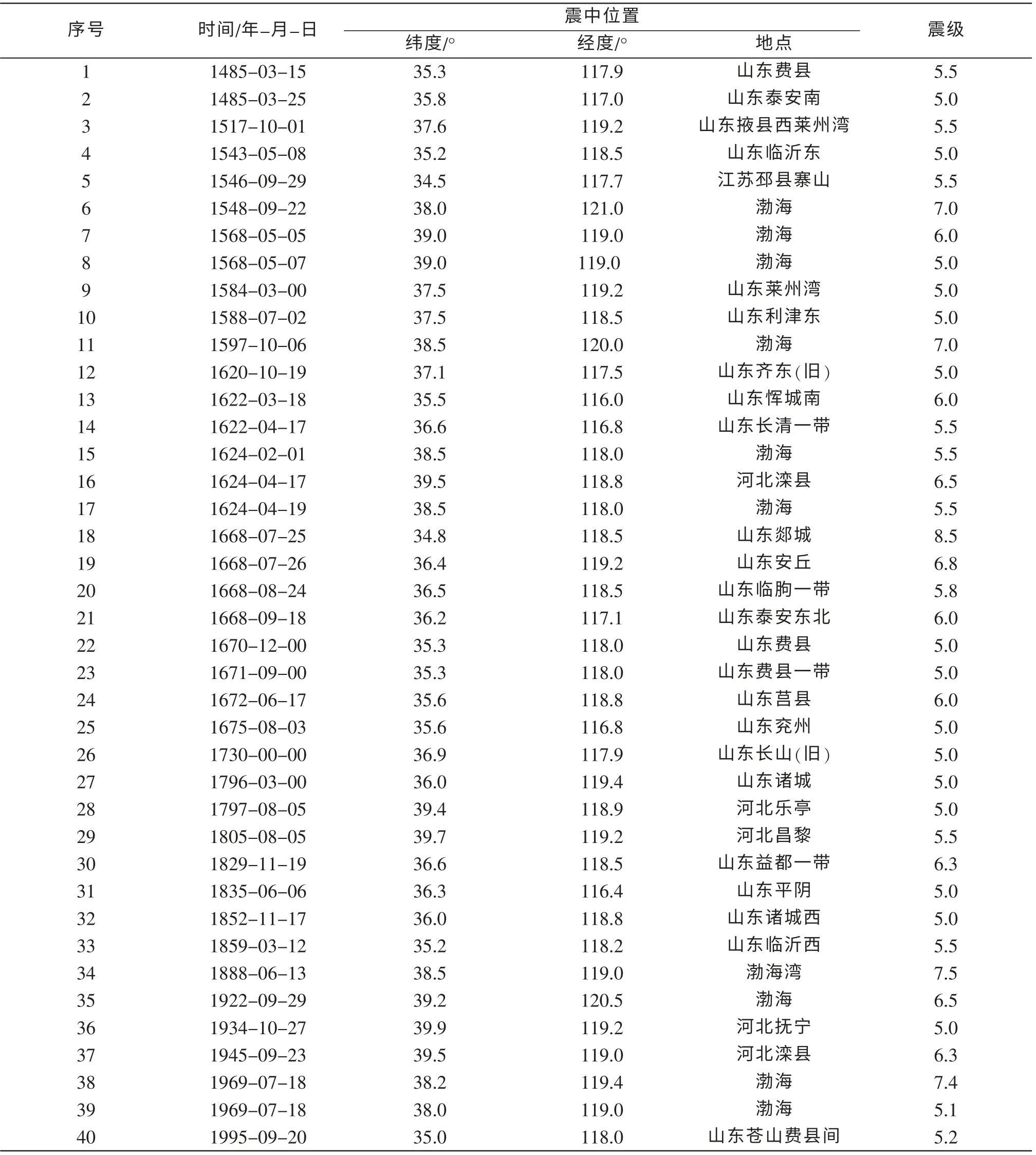
表2 郯庐地震带MS≥5.0 级以上地震目录Table 2 Catalogue of earthquakes with MS ≥5 in Tanlu seismic belt

图2 郯庐地震带1400年以来MS 5 级震中分布图Fig.2 Distribution map of epicenters of MS 5 earthquakes since 1400 in Tanlu seismic belt

2.1.2 经度外推

采用上述方法，按照表1 步骤，对郯庐地震带1 400年以来40 次地震经度进行分组计算，求各组周期的F 值，当取信度α＝0.01、 0.05、 0.10时，进行F 检验，均未找到显著周期。取信度α=0.20，进行F 检验，得到F8＝1.82＞F0.20(7，32）则8 组周期比较显著，为第一准周期。计算第一准周期各组平均值，找出准周期各组平均值的最小值，将各组平均值减去各组平均值当中的最小值作为第一准周期的特征值，得出第一准周期特征值分别为0.22、 0.38、 1.86、 0.72、 0.00、 0.94、 0.28、0.88。第一准周期特征值按序重复排列，将原经度序列对应减去第一准周期特征值，得出第一余差序列。

对第一余差序列再进行分组计算各组周期F值，当信度α＝0.01、 0.05、 0.10 时仍无显著周。取信度α=0.20，进行F 检验，得到F9＝1.81＞F0.20(8，31)。则余差1 中， 9 组周期比较显著，为第二准周期，计算第二准周期特征值分别为1.25、 1.22、 0.68、0.00、 0.48、 1.60、 1.14、 1.20、 1.46。将余差1 减去第二准周期特征值得第二余差序列。

对第二余差序列再进行分组，取信度α＝0.01、0.05、 0.10、 0.20 时，已无显著周期。

计算第二余差序列的均值（116.82）作为基值，将第一准周期特征值（0.22）、第二准周期特征值（0.48）、基值（116.82）叠加得外推预测值。具体结果见表3，由表3 可知，郯庐地震带下一次MS5级以上地震可能在东经117.52°附近。

2.1.3 纬度外推

用同样的方法，同理得出纬度的的第一准周期，在信度α=0.01 的情况下，得到F20＝3.10＞F0.01（19，20），第一准周期特征值分别为0.70、 0.50、 1.40、 0.35、0.00、 2.40、 2.45、 4.15、 3.55、 2.00、 2.35、 1.50、0.30、 2.50、 3.80、 4.65、 3.95、 1.45、 2.15、 0.70。对纬度余差1 求第二准周期， F9＝6.27＞F0.01(8，31)，第二准周期特征值分别为1.01、 2.01、 1.53、 0.60、0.23、 1.09、 1.73、 0.80、 0.00，对纬度余差2 再进行分组计算F 值，当信度α=0.01、 0.05 时，无显著周期。当信度α=0.10 时求得第三准周期， F14=1.84＞F0.10(13，26)。第三准周期特征值分别为： 0.62、0.00、 0.76、 0.80、 0.61、 1.03、 1.30、 1.34、 0.89、1.30、 0.95、 0.66、 0.91、 0.90。对纬度余差3 进行分组计算F 值，发现已无显著周期。

表3 郯庐地震带1400年以来MS 5 级以上地震方差周期法经度外推表Table 3 The longitude extrapolation table of variance cycle method for earthquakes with MS ≥5 since 1400 in Tanlu seismic belt

求余差3 的平均值作为基值，根据第一准周期特征值、第二准周期特征值、第三准周期特征值和最后的基值，进行外推预测，可知，该区域内下一个MS5 级以上地震可能发生在北纬34.95～35.00°附近。

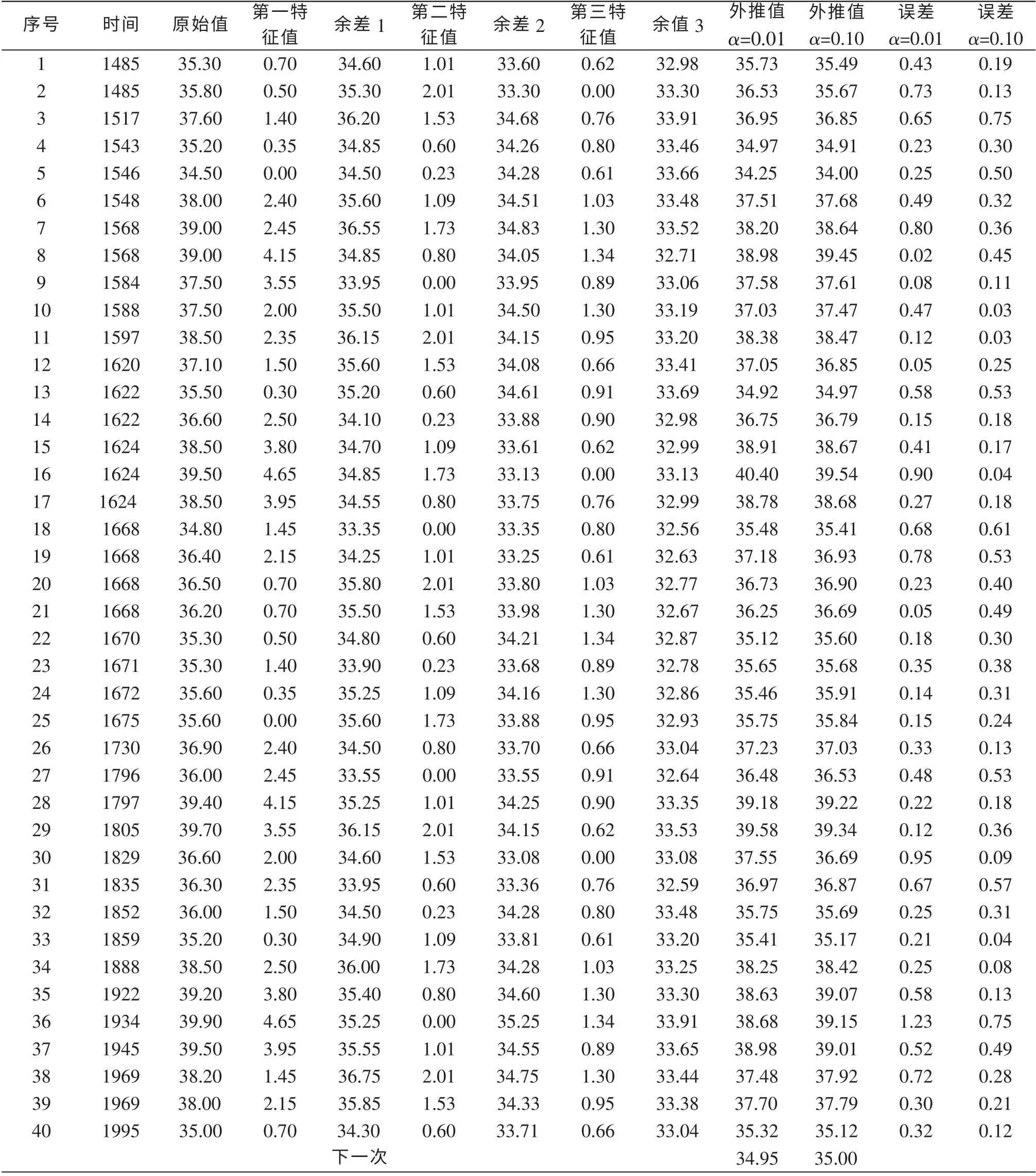
表4 郯庐地震带1400年以来MS 5 级以上地震方差周期法纬度外推表Table 4 The latitude extrapolation table of variance cycle method for earthquakes with MS ≥5 since 1400 in Tanlu seismic belt

图3、图4 分别是郯庐地震带1 400年以来MS5.0 级以上地震实测经、纬度与外推经、纬度对比曲线，从表3、表4、图3、图4 中可以看出，经度外推值与实测值之间误差较大，当信度α＝0.20时，误差绝对值在在0.04°～1.64°之间；纬度外推值与实测值误差较小，当信度α＝0.01 时，误差在在为0.02°～1.23°之间；当信度α＝0.10 时，误差在0.04°～0.75 之间。

2.2 其它地震区、地震带分析结果

用同样的方法对河北平原地震带、淮河地震带、北京-渤海地震带、华东地区、安徽地区、苏鲁皖交界地区进行方差分析，结果见表5、实测值与外推值对比曲线见图5～10。

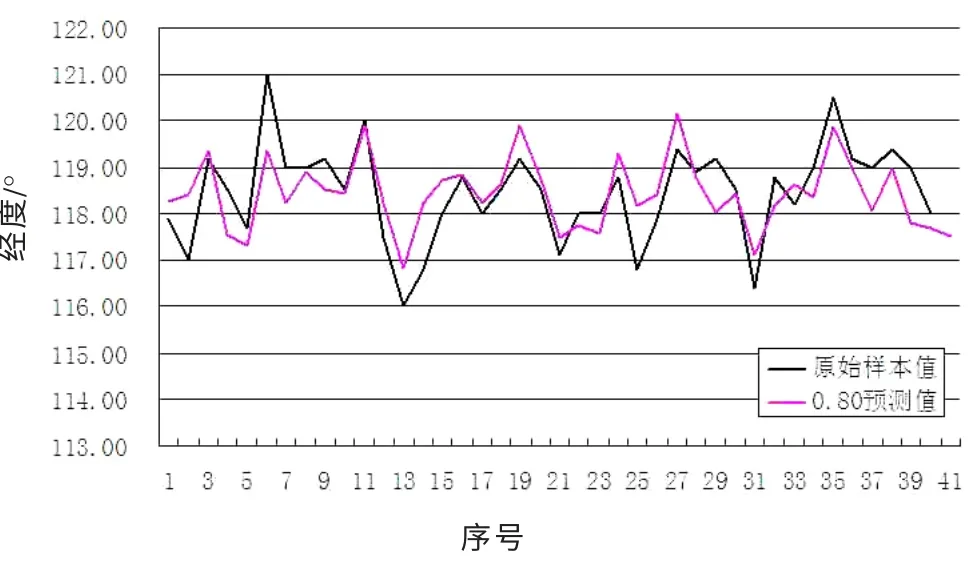
图3 郯庐地震带MS 5.0 级以上地震实测经度与外推预测值对比曲线Fig.3 The comparison curve between measured longitude and extrapolation predictive value for earthquakes with MS ≥5 in Tanlu seismic belt

图4 郯庐地震带MS 5.0 级以上地震纬度原始值与外推值对比曲线Fig.4 The comparison curve between the original value and extrapolated value of latitude of earthquakes with MS ≥5.0 in Tanlu seismic belt

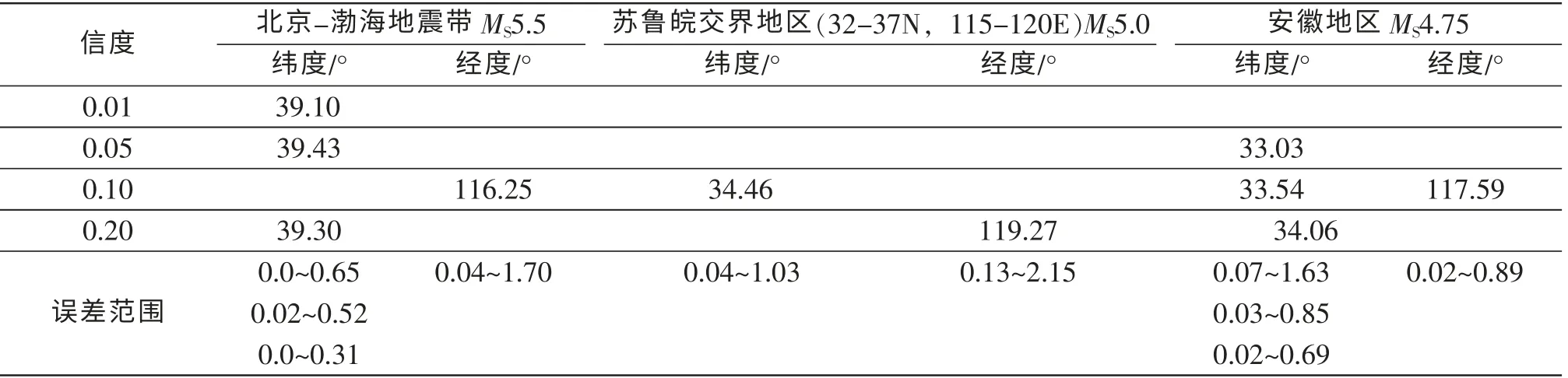
表5 北京-渤海地震带、苏鲁皖交界地区、安徽地区方差分析外推结果表Table 5 The table of variance analysis extrapolated results in Anhui-Bohai seismic belt, Jiangsu-Shandong-Anhui border area and Anhui region

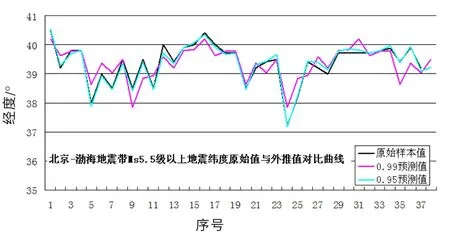
图5 北京-渤海地震带MS 5.5 级以上地震纬度原始值与外推值对比曲线Fig.5 The comparison curve between the original value and extrapolated value of latitude of earthquakes with MS ≥5.0 in Beijing-Bohai seismic belt

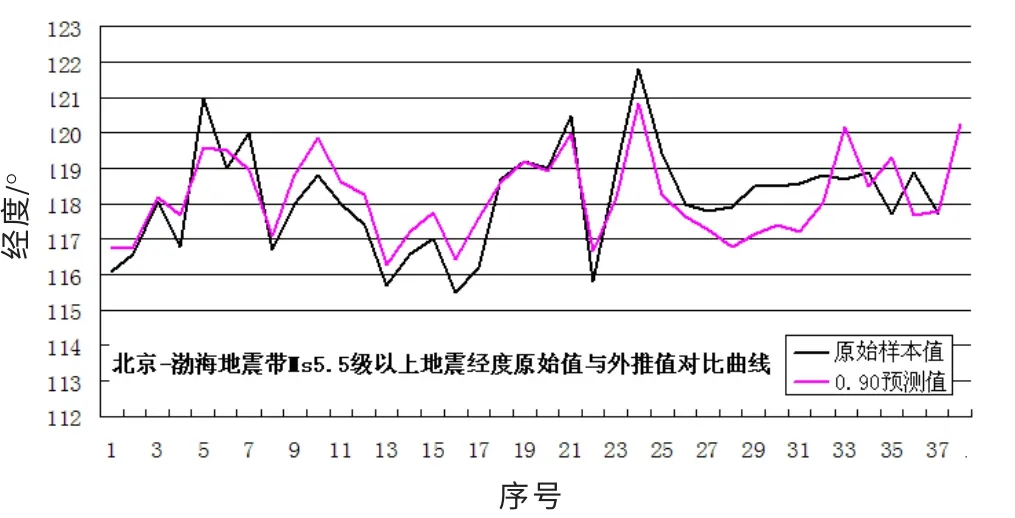
图6 北京-渤海地震带MS 5.5 级以上地震经度原始值与外推值对比曲线Fig.6 The comparison curve between the original value and extrapolated value of longitude of earthquakes with MS≥5.0 in Beijing-Bohai seismic belt

北京-渤海地震带MS5.5 级以上地震纬度取信度α=0.05、经度取信度α=0.10 时，外推该区域下一个MS5.5 级地震有可能发生在北纬39.43°、东经116.25°附近。苏鲁皖交界地区（32°～37°N， 115°～120°E）MS5.0 级以上地震方差分析外推结果显示，当纬度取信度α=0.10 时有显著周期，外推该区域下一个MS5 级地震在北纬34.46°附近；当经度取信度α=0.20 时存在显著周期，外推该区域下一个5 级地震可能发生在东经119.27°附近。安徽地区MS4.75 级以上地震纬度在信度α=0.05、0.10、 0.20 时均有显著周期，外推结果分别是北纬33.03°、 33.54°、 34.06°附近，经度在信度α=0.10时存在显著周期，外推结果东经117.59°附近。

图7 苏鲁皖交界地区MS 5.0 级以上地震纬度原始值与外推值对比曲线Fig.7 The comparison curve between the original value and extrapolated value of latitude of earthquakes with MS≥5.0 in Jiangsu-Shandong-Anhui border area

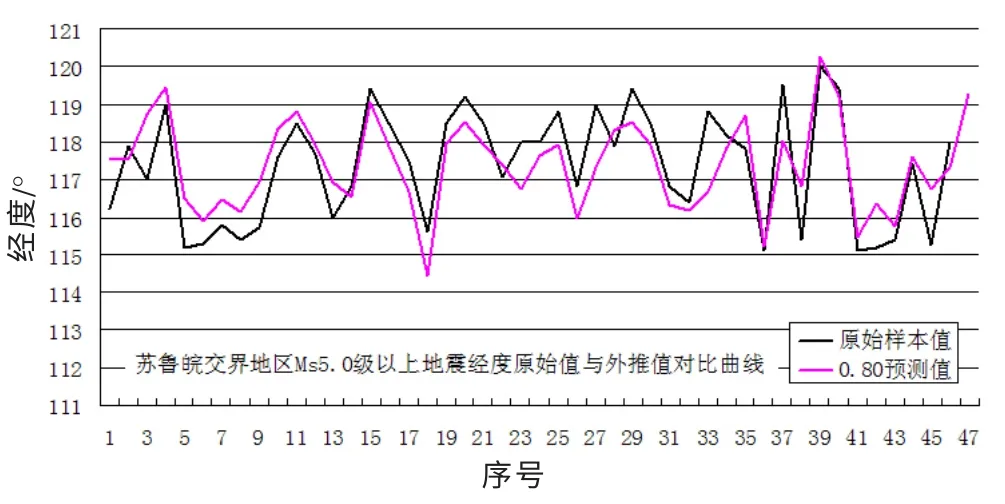
图8 苏鲁皖交界地区MS 5.0 级以上地震经度原始值与外推值对比曲线Fig.8 The comparison curve between the original value and extrapolated value of longitude of earthquakes with MS ≥5.0 in Jiangsu-Shandong-Anhui border area

图9 安徽地区MS 4.75 级以上地震纬度原始值与外推值对比曲线Fig.9 The comparison curve between the original value and extrapolated value of latitude of earthquakes with MS≥4.75 in Anhui region

图10 安徽地区Ms4.75 级以上地震经度原始值与外推值对比曲线Fig.10 The comparison curve between the original value and extrapolated value of longitude of earthquakes with MS≥4.75 in Anhui region

从表5 可知，纬度的周期性好于经度，且纬度的误差范围小于经度。也就是说纬度有较好的南北迁移特征。高信度的外推值误差范围大于低信度的外推值误差范围。

河北平原地震带、淮河地震带、华东地区MS5级地震纬度在某一信度下存在显著周期，但经度在α=0.01～0.20 范围内均不存在显著周期。

3 结语

（1）方差分析叠加周期外推法是数理统计上常用的方法，用于地震预测预报只是一种尝试。它可以用来研究地震震中在空间上的迁移特性，也可分析在时间序列、震级强度变化上是否具有周期性。

（3）通过对不同地区、不同震级的地震采用方差叠加周期外推法分析，结果显示，郯庐断裂带5 级、北京-渤海地震带5.5 级、苏鲁皖交界地区5 级、安徽地区4.75 级以上地震在α=0.01～0.20范围内存在显著周期，可以外推出下一次地震的预测范围。另外，河北平原地震带、淮河地震带、华东地区MS5 级地震纬度在某一信度下存在显著周期，但经度在α=0.01～0.20 范围内均不存在显著周期。

方差分析叠加周期外推法对某些范围内对存在显著周期的地震能够进行外推预测，对某些范围内不存在显著周期的地震不能够进行外推预测。能否进行外推预测，主要取决于某一序列的数据是否具有显著周期。

（3）外推预测值与实测原始值存在一定的误差，纬度的误差范围小于经度的误差范围。且对于同一序列的数据，信度增高，外推值的误差范围扩大，信度降低，外推值的误差范围缩小。不同区域地震方差分析结果显示，纬度的显著周期高于经度，说明纬度有较好的南北迁移特征。

（5）方差分析叠加周期外推法的意义在于应用统计理论上把预测地点进行了定量化，缩小了监视范围。从某种意义上，还为研究地震机理，探索地震在时、空、强的演变规律上，提供研究方向。

［1］车文，宫英丽. 方差分析滤波法在时间序列预测分析中的应用[J]. 数理医学杂志， 2001， 14（2）： 157-159.

［2］杜晓林. 概率论与数理统计[M]. 北京：气象出版社,2005.

［3］邓韫. 地震周期的存在及形成机制讨论[J]. 华南地震，2003， 23（01）： 51-56.

［4］王国英. 关于地下水氡浓度的周期变化-水氡潮[J]. 华南地震， 1982， 1（04）： 63-69.

［5］柯龙生. 地震活动周期的谱分析[J]. 华南地震，1989， 9（1）： 17-22.

［6］杨长登. 用方差分析周期叠加外推法在预报年降水量[J]. 贵州气象， 1998， 22（1）： 23-25.

［7］邢兰辉，吕惠萍，张锦辉. 周期叠加方差分析法预报河川径流量[J]. 水文， 2007， 27（4）： 41-44.

［8］张绍治. 多因子方差分析BASIC 程序[J]. 华南地震,1988， 8（1）： 67-72.

［9］李起彤，南金生，苏顺昌，等. 华东地区中强地震构造背景和地质标志研究[J]. 华南地震， 1990， 10 (1)：1-14.