套管接箍定位器弹簧刚度计算方法探讨

陈　智，张　炎，于东兵，胡强法，张友军，辛永安

套管接箍定位器弹簧刚度计算方法探讨

陈智，张炎，于东兵，胡强法，张友军，辛永安

（中国石油集团钻井工程研究院江汉机械研究所，湖北荆州434000）①

从单片弓形弹簧刚度的计算方法入手，运用数理统计学方法分析试验数据，找出单片弹簧刚度与组合弹簧刚度之间的关系，得出了组合弓形弹簧刚度的计算方法。用该方法得出每种组合弹簧刚度的计算值，将计算值与实测值进行对比，发现本方法得到的计算值与实测值偏差为-2.9%～9.3%，平均偏差为0.5%。计算值接近实测值，说明本方法可靠性较高，具有较好的工程实用价值。

套管接箍定位器；组合弓形弹簧；刚度

在目前的井下作业施工工艺中，套管接箍定位器作为一种辅助工具，已大量用于井下管柱的定位［1-3］。套管接箍定位器所用的弹簧为多片叠加的组合弓形弹簧，其刚度计算方法正被相关工程技术人员所研究，但截至目前，并无相关研究内容公开。笔者参与研究的项目涉及到套管接箍定位器的设计和使用，根据设计和使用经验，笔者总结出一种简单易行、可靠性较高的组合弓形弹簧刚度计算方法，可满足工程应用要求。

1　弹簧刚度的计算方法

1.1套管接箍定位器弹簧

套管接箍定位器所用的弹簧为多片叠加的组合弓形弹簧，结构如图1所示，其受力与变形的关系式较难推导，亦即弹簧的刚度计算公式较难得出。

图1　组合弓形弹簧结构

笔者通过选取一种单片弓形弹簧刚度的计算方法入手，并结合后续试验结论，推导出一种组合弓形弹簧刚度的计算方法。

1.2单片弓形弹簧的刚度计算方法

单片弓形弹簧结构如图2所示。

图2　单片弓形弹簧结构

［4］可知，弓形弹簧的径向位移与径向力之间的关系式为

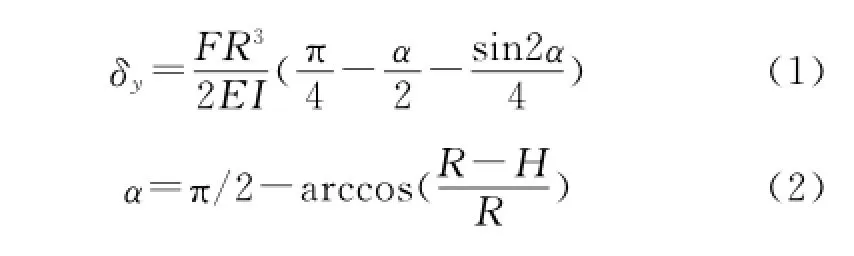
式中：δy为弓形弹簧的径向位移；F为弓形弹簧受到的径向力；E为弓形弹簧材料的弹性模量；I为弓形弹簧横截面的惯性矩；α为设计中间参数；R为弓形弹簧中性层的弯曲半径；H为弓形弹簧的弓高。

因弓形弹簧横截面为矩形，由《材料力学》［5-6］相关公式可知弓形弹簧横截面的惯性矩为

式中：b为弓形弹簧的宽度；h为弓形弹簧的厚度。则式（1）变形可得

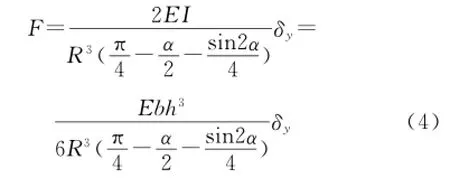
参照弹簧的刚度定义可知，单片弓形弹簧的刚度k的计算公式为

1.3单片弓形弹簧的刚度计算

实际设计中，取E=210 GPa［7-8］，b=25.3 mm，h=0.8 mm，R=42.8 mm，H=11.6 mm。将上述参数代入式（2）可得α=0.817 rad，再分别代入式（5），计算可得单片弓形弹簧的刚度k=45.4 N／mm。

2　组合弹簧刚度的试验及数据分析

2.1试验结果

对1批弹簧样品进行了刚度测试，分别按1片、2片、3片、4片、5片组合，1片弹簧试验2组，其余试验1组。每种组合弹簧在初始高度至工作高度范围内取5个点测试，由试验机直接读出所加载荷，用游标卡尺测量弹簧高度，试验数据处理结果如表1所示。

表1　组合弹簧刚度试验结果　N／mm

2.2线性相关性分析

将表1所列的组合弹簧刚度实测值与组合弹簧的片数进行线性相关性分析，分析结果如表2所示。

表2　组合弹簧刚度与弹簧片数的线性相关性分析

由表2可知：相关系数ρxy=0.988 16≈1，说明组合弹簧刚度与弹簧片数之间存在紧密的线性相关性［9］，证明了组合弹簧刚度与弹簧片数基本成正比关系，即组合弹簧刚度≈单片弹簧刚度×弹簧片数。

2.3刚度计算公式

根据表1所列的各种组合弹簧刚度的平均实测值46.7、100.8、157.3、198.8、221.4 N／mm，与前述的单片弹簧刚度计算值45.4 N／mm，算出二者之间的倍数值，分别为1.029，2.22，3.465，4.379，4.877。

再根据算出的倍数值与弹簧片数拟合出修正系数曲线，如图3所示。拟合优度R2=0.989，说明拟合程度高。

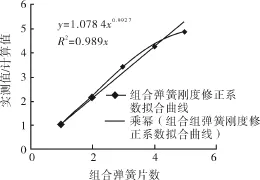
图3　组合弹簧刚度修正系数拟合曲线

结合式（5）与图3得出的修正系数拟合曲线，则组合弓形弹簧刚度计算公式为

式中：x为组合弓形弹簧的片数。

2.4计算值与实测值对比分析

当弹簧片数x分别为1、2、3、4、5时，则由式（6）可算出每种组合弹簧的刚度值分别为49.0、97.4、145.7、193.9、241.9 N／mm。将计算的弓形弹簧刚度值与表1列出的平均实测值进行对比，结果如表3所示。

表3　计算值与实测值对比

由表3可知：用式（6）算出的弓形弹簧刚度值与实测值偏差为-2.9%～9.3%，平均偏差为0.5%，计算值接近实测值，具有较好的工程实用价值。

3　结语

运用数理统计学方法，对1批弹簧样品的试验数据进行数理统计分析，得出较强的数理统计学结论［10］，此结论具有较强的合理性。本文总结出来的套管接箍定位器弹簧刚度的计算方法简单易行，可靠性高，计算值与实测值偏差为-2.9%～9.3%，平均偏差为0.5%，具有较好的工程应用价值，值得推广应用。

［1］韩振强，王中伏.套管扶正器性能检测技术及应用［J］.钻采工艺，1996，19（1）：43-45.

［2］胡强法，朱峰，张友军.零半径水射流径向钻井技术的研究与应用［J］.石油机械，2009，37（5）：12-15.

［3］崔龙连，汪海阁，葛云华，等.新型径向钻井技术［J］.石油钻采工艺，2008，30（6）：29-33.

［4］陈智，丛强，胡强法，等.一种弓形弹簧的设计与应用［J］.石油机械，2010，38（8）：71-73.

［5］刘鸿文.材料力学［M］.3版.北京：高等教育出版社，1992.

［6］苏翼林.材料力学：上册［M］.北京：高等教育出版社，1979.

［7］成大先.机械设计手册［K］.4版.北京：化学工业出版社，2002.

［8］毛谦德，李振清.袖珍机械设计师手册［K］.北京：机械工业出版社，1994.

［9］盛骤，谢式千，潘承毅.概率论与数理统计［M］.2版.北京：高等教育出版社，1989.

［10］方开泰，马毅林，吴传义，等.数理统计与标准化［M］.北京：技术标准出版社，1979.

Discussion on Calculation Method of Casing Collar Locator Spring Stiffness

CHEN Zhi，ZHANG Yan，YU Dongbing，HU Qiangfa，ZHANG Youjun，XIN Yongan
（Jianghan Machinery Research Institute，CNPC Drilling Research Institute，Jingzhou 434000，China）

Beginning with calculation method of the single bow spring stiffness，the test data by means of mathematical statistics is analyzed，and the relationship between the single spring stiffness and the combined spring stiffness find out.Finally a conclusion of the calculation method of composite bow spring stiffness was made.And this method is used to calculate the design value of each combined spring stiffness，comparing the design values with the measured value，find that the deviation between design calculated value and measured value is-2.9%～9.3%，the average deviation is 0.5%and the design value is close to the measured values，which shows that this method has high reliability，good practical engineering value.

casing collar locator；composite bow spring；stiffness

TE931.2

A

10.3969／j.issn.1001-3482.2015.10.012

1001-3482（2015）10-0050-03