墙后填土面的倾角大于内摩擦角分析处理
2015-08-03钟桂文吴海波
钟桂文,吴海波,杨 志
(1.重庆甲多公路设计咨询有限公司;2.中交二公局第一工程有限公司;3.重庆市规划局九龙坡分局)
1 引 言
重庆市东港港区疏港大道起点与东西干道起点相接,终点与南北干道终点相接,整体走向由南向北,全长2.965 km,路幅宽34 m,双向6 车道,设计速度60 km/h。
该施工段岩层呈单斜产出,地质结构总体上相对简单,地形平缓。但有部分施工段边坡较陡,如K2 +300~K2 +420 基岩坡度主要由两部分组成:K2 +300~K2 +330 m 段基岩坡度相对较缓,倾角大于10°~20°,K2 +330~K2 +420m 段基岩坡度较陡,倾角20°~30°,该施工段(K2 +300~K2 +420)总体上坡度较陡,岩层结构较完整。若开挖改变边坡原有结构,则影响边坡稳定性,需采取挡土墙加固边坡措施。
采用库伦土压力理论计算土压力,但当φ <β 时,库伦土压力系数K 无法计算。可用朗金土压力理论,将荷载由三角形分布转化为矩形分布。
2 朗金土压力理论
2.1 朗金土压力理论
朗金土压力理论,是通过研究弹性半空间体内的应力状态,根据土的极限平衡条件得出的计算方法。
适用条件:挡土结构墙背垂直、光滑、挡土结构物刚性、挡土结构物墙后填土为均质刚塑性半无限体、挡土结构物墙后填土面水平、墙高以下的土体状态及位移与其上的一致。
(1)主动土压力
根据土的强度理论,当土体中某点处于极限平衡状态时,取单位墙长计算,则主动土压力为:
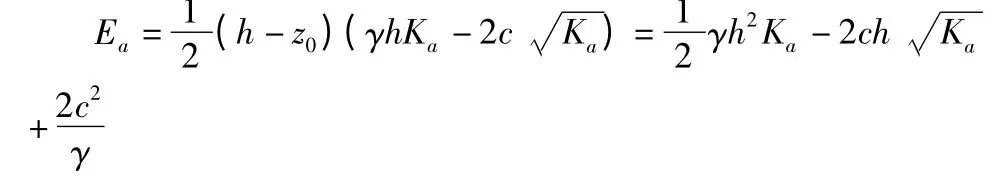
主动土压力Ea通过三角形压力分布图的形心,即作用在墙底(h-Z0)/3 处。
(2)被动土压力
当挡土墙在外力作用下挤压土体出现被动朗金状态时,总被动土压力为:
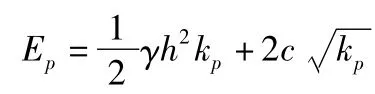
(3)填土表面有连续均布荷载
当挡土墙后填土表面有连续均布荷载q 作用时,一般可将均布荷载换算成位于地表以上的当量土重,当量的土层厚度h'为:h'=q',再以h+ h'为墙高,按填土面无荷载情况计算土压力。
3 处理方案
内摩擦角φ <墙后填土面的倾角β,此时,用朗金土压力计算,墙后填土分布为三角形,取最大荷载为q1,长为L,将三角形荷载转化为矩形荷载,用郎金土压力计算土压力。计矩形荷载为q2,长为L,如图1 所示:
取q2=2/3q1,以下是计算的推导:
首先,要确认结构体系是可以用叠加方法的。这一点很重要,工程结构体系均考虑可以通过叠加方法计算。由于结构体系可以用叠加方法运算,在推导时,我们将挡墙受力看成悬臂梁分布,三角形荷载(如图1)在悬臂梁产生的最大弯矩为:Mmax1=1/3q1L2
矩形分布悬臂梁产生最大弯矩为:Mmax2=1/2q2L2
令最大弯矩相等,即Mmax1=Mmax2,得出q2=2/3q1,也就是说,当我们把三角形荷载最大值(q1)乘以2/3,转换为矩形荷载分布,它们在梁中产生的最大弯矩是相等的。这样我们可以转化成矩形分布荷载,用郎金土压力理论解决内摩擦角φ <墙后填土面的倾角β 问题。
在工程计算中,还要顾及剪力,或者说是支座反力。将三角形荷载最大值乘以2/3 ,转换矩形荷载看是否影响梁的剪力(支座反力)那么我们继续以图1 进行深入探讨。三角形荷载(图1)在悬臂梁上的支座反力为:T1=1/2q1L,矩形荷载(图1)在悬臂支梁上的支座反力为:T2=q2L=2/3q1L,很明显,T2>T1,也就是说荷载的变化会引起支座反力(剪力)增大,这是偏于安全的。
由上的推导,我们可以得出这样的结论:把三角形荷载最大值乘以2/3 变为矩形荷载是可行的。
由朗金土压力理论,当挡土墙后填土表面有连续均布荷载q2作用时,一般可将均布荷载换算成位于地表以上的当量土重,当量的土层厚度h'为:h'=q2,再以h+ h'为墙高,按填土面无荷载情况计算土压力。
4 工程应用
在该项目中,墙后填土面的倾角β=37°,土壤为中风化砂岩,[σ]=1 500 kPa,基底摩擦系数为f 在0.6~0.7 之间,取0.6。墙背填土材料为砂岩石屑填料,内摩阻角=35°。容重γ=20 kN/m3,墙体材料用7.5 号砂浆砌30 号片石,砌石γr=22 kN/m3,砌石允许压应力[σr]=800 kPa,允许剪应力[τr]=160 kPa。设计稳定系数[Kc]=1.3,[K0]=1.5。山坡挡墙设计断面图如上述图2、图3 所示。
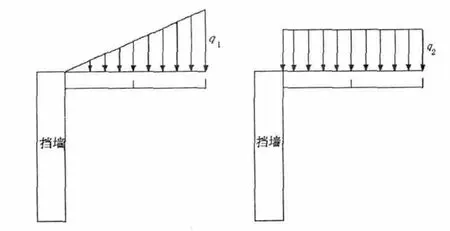
图1 三角形荷载
4.1 尺寸拟定及模型建立转换
(1)断面尺寸的拟订
根据横断面的布置,该断面尺寸如图4 所示:
B1=1.65 m B2=1.00 m B3=3.40 m B=4.97 m N1=0.2 N2=0.2 N3=0.05 H1=7.00 m H2=1.50 m H=9.49 m d=1.6 m α=arctan N1=arctan0.2=11.3 δ=17.5 °
(2)模型建立及转换
根据朗金理论,将图3 的q2(山坡三角形荷载分布等效矩形荷载)换算等代均布土层厚度h0,由勘察设计得q1最大值为20.625 kN/m2,则由上述推导可得,可取为2/3,即q2=2/3q1,即q2=2/3 ×20.625=13.75 kN/m2,h0=0.687 5m,γ为墙背填土重度。
4.2 挡土墙稳定性验算
(1)土压力计算
假定破裂面交于荷载内,采用《路基设计手册》(第二版)表3-2-1 主动土压力公式计算:
ω=φ+α+δ=63.8° A=-0.178
tanθ=-4.566 7 或0.500 取θ=26.58
tgθ×H+tgα×H=0.5 ×9.49 +0.2 ×9.49=6.643 >1.6假设成立,破裂面交于荷载内。
Ka=0.333 h1=2.285 K1=1.11 Ea=333.21 kPa
Ex=291.96 kPa Ey=160.57 kPa ZX=3.23 m ZY=B-ZXtanα 4.32 m
(2)抗滑稳定性验算
KC=1.453≥[KC]=1.3 抗滑稳定性满足要求。
(3)抗倾覆稳定性验算
K0=22.63≥[K0=1.5 抗倾覆稳定性满足要求。
(4)基底合力及合力偏心距验算
e=0.82 ≤[e0]=1.24 σ1=283.145 σ2=1.43 σmax=301.12 kPa <[σ]=1 500 kPa
基底合力及合力偏心距满足要求。
5 结 论
通过对朗金土压力理论适用范围分析,在φ <β 情况下,库伦土压力已不再适用。可将墙后填土看成三角形荷载,再转换成矩形分布。均布荷载可取三角形荷载最大值的2/3。经受力分析,取值合理。可运用到具体工程实例,具有实际的工程意义。
[1]赵明华,俞晓..土力学与基础工程[M].武汉理工大学出版社,2003.
[2]中华人民共和国国家标准.湿陷性黄土地区建筑规范(GBJ25-90)[S].北京:中国计划出版社,1991.
[3]张雨化.道路勘测设计[M].北京:人民交通出版社,1997.
[4]中华人民共和国国家标准,岩土工程勘察规范(GB50021-2001)[S].北京:中国建筑工业出版社,2001.
