一种自适应变分贝叶斯容积卡尔曼滤波方法
2015-08-02沈锋徐广辉桑靖
沈锋, 徐广辉, 桑靖
(哈尔滨工程大学自动化学院,黑龙江哈尔滨150001)
一种自适应变分贝叶斯容积卡尔曼滤波方法
沈锋, 徐广辉, 桑靖
(哈尔滨工程大学自动化学院,黑龙江哈尔滨150001)
针对应用于非线性系统模型的容积卡尔曼滤波工作性能会受观测噪声参数变化的影响而降低的问题,提出一种自适应的变分贝叶斯容积卡尔曼滤波算法。在每一次更新步骤中,将系统状态与变化的观测噪声统计信息一起作为随机变量,并用变分贝叶斯方法进行估计,在迭代逼近得到噪声方差后,再利用容积卡尔曼滤波对系统状态进行更新。仿真实验证明变分贝叶斯容积卡尔曼滤波算法在非线性系统的滤波问题中能够较好跟踪变化的观测噪声方差,相比容积卡尔曼滤波拥有较好的估计性能。
变分贝叶斯;容积卡尔曼滤波;自适应;非线性系统
0 引 言
作为卡尔曼滤波的衍生,扩展卡尔曼滤波(EKF)、无迹卡尔曼滤波(UKF)、容积卡尔曼(c KF)等成熟的非线性滤波算法自提出以来已经受到了广泛而深入的研究[1-2]。但此类非线性滤波算法在实际非线性系统的应用中会有一定的局限性,原因在于这些算法本身的建立依赖于准确的模型、确定的系统参数、已知的噪声统计特性,而在实际工程领域,由于人们对工况的认知有限,建模可能会出现误差,即使模型参数、噪声统计特性得到确定,在系统实际运行中,系统本身存在摄动,同时容易受到外界的干扰,系统噪声或观测噪声也可能随之发生变化,这种情形下,此类非线性滤波器的工作性能会发生退化,极端情形下甚至无法正常工作。
针对这种情形,自适应的滤波算法开始受到了关注。就目前的研究方法来讲,自适应滤波算法主要有贝叶斯法、最大似然法、相关法以及协方差匹配法[3]。其中,相关法由于它在计算上的相对便捷,受到了更多关注与研究。而事实上,后3种方法都可以视为自适应滤波算法在贝叶斯框架下的特例,它们在广义上都属于贝叶斯法。然而,在贝叶斯法中,由于涉及概率密度函数的计算,积分项都过于复杂,一般情况下难以得到确定的解析解。这使得贝叶斯法通常只能在理论上得到解释,而在实际应用上则显得非常有限。
通常情况下,在贝叶斯准则的基础上,采样方法被引入用以随机逼近得到近似的精确的参数或模型。一个比较典型的方法便是蒙特卡洛马尔可夫链McMc(Monte carlo Markov chain)方法。它通过构造马尔可夫链(Markov chain)的极限不变分布来模拟高维数的积分运算[4]。然而McMc等随机采样方法的估计精确度是以牺牲计算量为代价的,在许多实时性要求较高的工程应用领域有很大的局限性,而且如何判定马尔可夫链的收敛也是一个难题。
除了随机逼近,还有一类被称作确定性逼近的方法,变分贝叶斯方法便是其中的一种。Attias H在文献[5]中的详细论述被认为是变分贝叶斯方法最早的理论体系。该方法提议引入一个新的形式简单的分布,通过迭代更新变分参数,不断最大化待估计参数的边缘似然函数的下界来逼近参数的真实后验分布,直至算法收敛。
虽然变分贝叶斯方法在提出之初的几年里普遍是用于系统模型的参数估计,但是近几年,因为变分贝叶斯方法相比McMc等采样方法在估计上的快速性,使得它的应用领域已经从图像处理[6]、盲源分离[7]、语音增强[8]、信道估计[9]等参数推断领域延伸到了状态估计领域,如今,在滤波问题方面,变分贝叶斯方法也受到了许多学者的关注和研究: Vrettas M D将变分贝叶斯方法用于随机动态系统的参数估计问题当中[10];Boujemma A将变分贝叶斯方法用于动态断面X射线照相术的卡尔曼滤波之中[11];Sarkka S提出了将变分贝叶斯方法用于估计经典卡尔曼滤波算法中的观测噪声[12];Sun J L则通过变分贝叶斯,设计了针对未知系统输入下的两步卡尔曼滤波器[13];孙世军则用基于时间序列的变分贝叶斯方法用于盲源分离问题之中去估计源信号与混合矩阵[14]。
本文在文献[12-13]的研究成果的基础上,针对工程领域中普遍存在的非线性系统模型,用概率的方法,从广义贝叶斯滤波角度着重设计了基于变分贝叶斯的噪声自适应容积卡尔曼滤波器。该滤波器可以自适应地运用变分贝叶斯方法,动态地跟踪观测噪声,从而有效地提高估计精确度。文中首先给出变分贝叶斯学习的基本原理,并简单的阐述了容积卡尔曼滤波方法;接着给出了本文所提出的变分贝叶斯容积卡尔曼滤波方法原理及实现步骤,并对与传统的容积卡尔曼滤波方法进行了计算机仿真对比;最后给出了结论。
1 变分贝叶斯
在参数估计的问题中,在获得了观测样本的数据集Z后,根据贝叶斯准则,核心是参数集θ的后验概率密度函数的计算
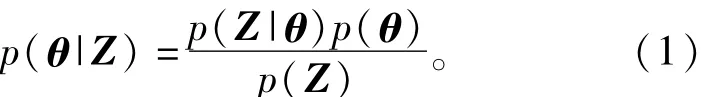
而式(1)计算的一个难点在于分母,边缘似然概率密度函数p(Z)的计算。正如引言所述,通常情况下p(Z)的计算难以得到精确的解析解,引入变分贝叶斯方法,引入一个简单的近似分布函数q(θ),并取p(Z)的对数形式:
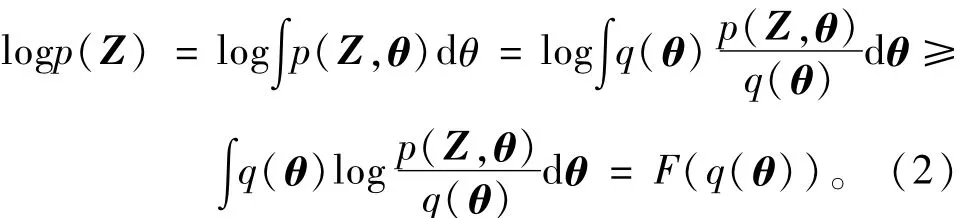
另一方面,又有
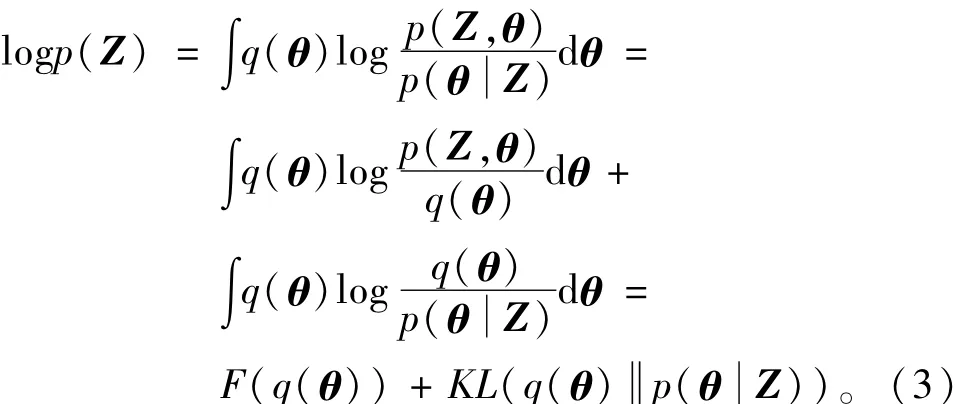
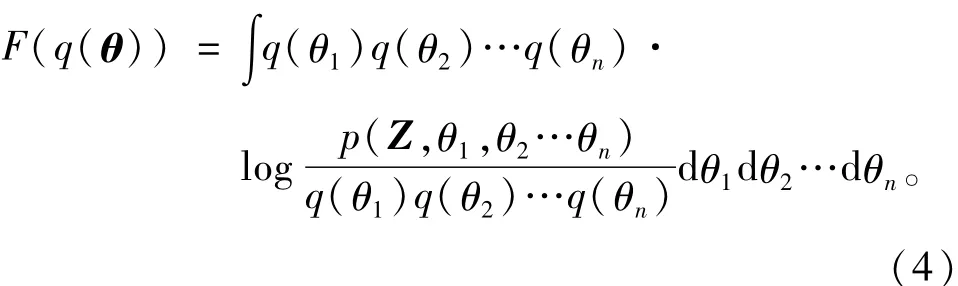
通过求偏导,可以得到F(q(θ))的极值,其通解表达式为[4]

可以发现,每个参数θi的近似分布可以通过求对数联合概率密度函数关于其他参数分布q(θj≠i)的期望求得,所以每一个参数分布的计算都依赖于其他参数的分布。这就形成了迭代的机制:在给定先验知识的情况下,初始化参数值,通过变分贝叶斯算法循环迭代计算,进行参数更新,直至自由能量(对数边缘似然函数的下界)达到最大值,判定算法收敛并结束,此时可以得到系统模型参数的估计值。
2 容积卡尔曼滤波

针对所有离散的线性与非线性状态空间模型,它们的概率表示形式如下:与代表了一般贝叶斯意义下的系统状态方程与系统观测方程。对于非线性系统,考虑加性的系统噪声与观测噪声,分别有其中与h(xk)为非线性函数,wk~N(0,qk),vk~N(0,rk)均服从高斯分布。所以,对于状态空间模型有
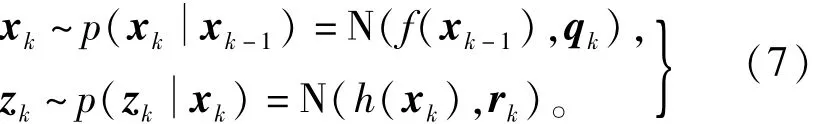
而状态变量xk服从均值为mk,协方差为Pk的高斯分布,即于是,在k-1时刻观测后,先验概率而在k时刻观测后,后验概率所以,在递归的容积卡尔曼滤波算法中[17],有
预测方程:
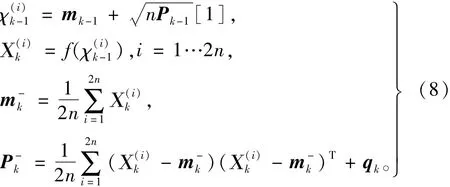
更新方程:
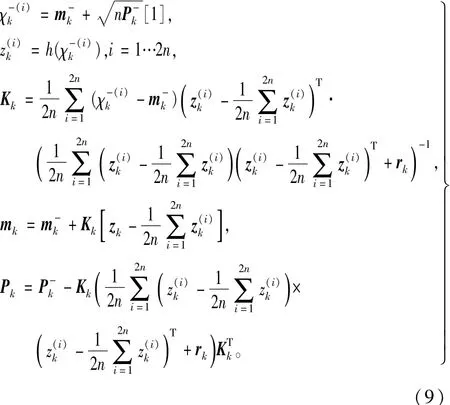
3 变分贝叶斯容积卡尔曼滤波
在容积卡尔曼滤波中,观测噪声的统计矩信息被认为是确定的,且保持不变。现在在变分贝叶斯容积卡尔曼滤波算法中,把动态观测噪声的方差rk和状态变量xk当作随机变量,作为待估计的参数。在k-1观测时刻后,两者的联合概率密度函数的先验分布为

在k时刻观测后,联合概率密度函数的后验分布为
这样,式(10)与式(11)就构成了广义贝叶斯滤波理论的预测方程和更新方程。但是除了一些比较简单的情形,式(10)与式(11)当中的积分运算很难得到解析解,所以引入变分贝叶斯方法求其次优近似解。
随机变量xk与rk被认为相互独立,根据先验知识,认为它们分别服从高斯分布与逆Gamma分布。因此在k-1时刻后,
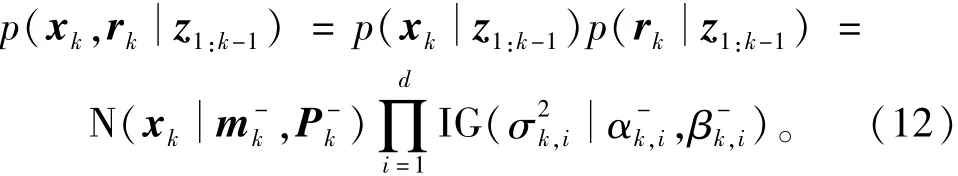
经历了第k时刻的观测后,在变分贝叶斯方法中,引入一个新的分布来代替真实的后验分布为了推导的简洁,文章后面在写法上均略去了新的分布对于观测量z1:k的依赖,同时考虑到两个变量相互独立,所以同样对于联合概率密度函数的近似分布有q(xk,rk)=q(xk)q(rk)。
式(5)给出了变分贝叶斯方法近似解的通解表达式,采用容积卡尔曼滤波算法中一样的处理方法,对hk(.)的线性化处理,对于状态变量:
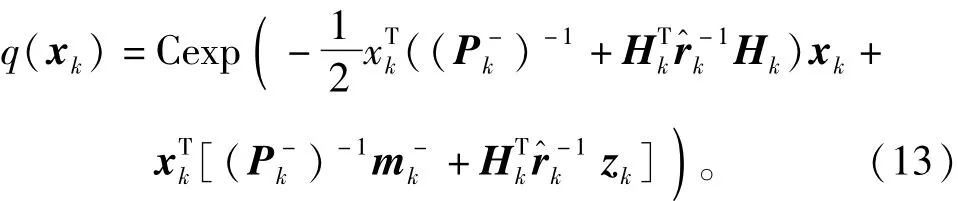
而对于观测噪声的方差:
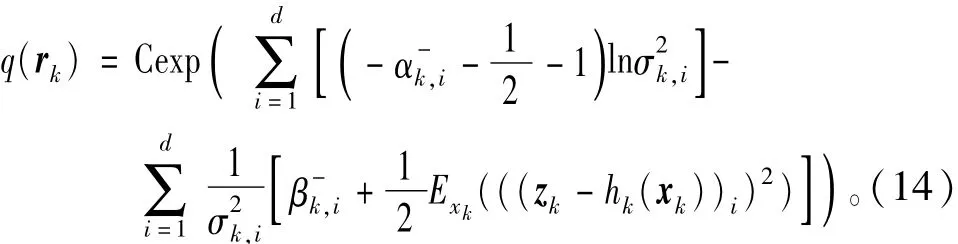
其中,c是一个与分布形式无关的常数。可以发现,式(13)与式(14)在形式上分别是高斯分布与逆Gamma分布,只是参数与先验分布的不同。这是因为选取的高斯分布与逆Gamma分布都属于共轭指数分布域,而正是共轭性保证了变量在先验分布与后验分布在形式上的一致性[15]。
近似的高斯分布的参数拥有如下表达式:
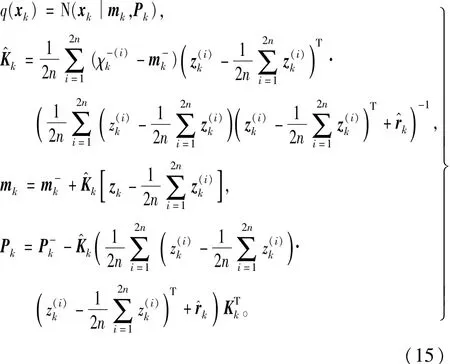
其中
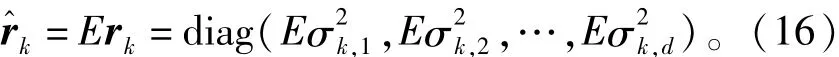
近似的逆Gamma分布表示为

注意到在(18)中,方差阵对角线上元素的期望的计算需要已知的逆Gamma分布的信息,根据逆Gamma分布的性质,即
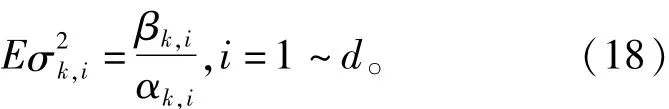
而在(19)中,根据容积卡尔曼的采样策略,期望部分可以继续展开如下:
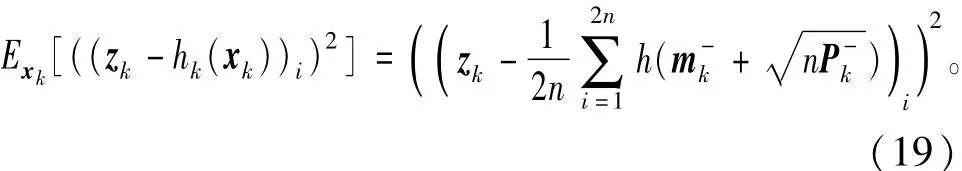
于是,式(13)~式(19)就构成了全部对观测噪声rk与系统状态变量xk进行联合估计的变分贝叶斯算法的步骤:首先给定先验知识并初始化各分布参数,然后开始对近似分布和各个期望进行迭代计算,得到更新的分布式(13)与式(14)后,分别计算参数在分布下的新的期望式(18)与式(19),进而再利用式(15)与式(17)中的更新方程对分布参数进行更新。如此循环迭代计算,直至算法收敛,得到逼近的估计值。
在用变分贝叶斯方法得到估计的观测噪声方差后,可以将其与容积卡尔曼滤波算法相融合,对非线性系统模型进行自适应的容积卡尔曼滤波处理,滤波算法总结如下。
初始化:
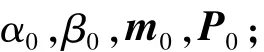
预测步骤:
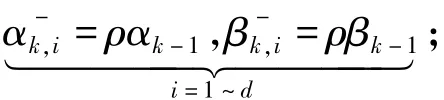
式(8);
更新步骤:
式(15)~式(19);
需要指出的是在预测步骤中,对于超参数αk-1与βk-1的预测,借鉴了文献[12]中观测噪声方差的建模方法,这样使得观测噪声的方差的分布参数能够平稳地发生变化。其中ρ是一个在(0,1]内的变化因子。而对比容积卡尔曼滤波器,该滤波器在预测步骤中对噪声方差进行动态建模,在更新步骤中先用变分贝叶斯方法,迭代地估计观测噪声的方差,并在得到噪声的统计信息后对系统的状态进行更新,如此反复直至滤波算法结束。
4 仿真分析
为了验证变分贝叶斯容积卡尔曼滤波器(VB-c KF)的性能,用设计的滤波器去考察一个存在变化噪声方差的非线性模型:
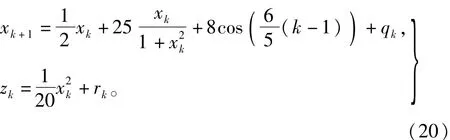
其中rk为待估计的、不确定的、服从高斯分布的白噪声的方差。本实验中,在[1:200]、[201:400]、[401:600]时刻,依次取rk为1、5、3,并分别用容积卡尔曼滤波器(c KF)与设计的滤波器进行性能比较。
图1列出了在实验中,容积卡尔曼滤波算法和变分贝叶斯容积卡尔曼滤波算法对状态跟踪的对比,图中用状态的均方根误差作为纵轴,仿真次数作为横轴。从中可以看出,由于人为地取观测噪声的方差值使之发生波动,而容积卡尔曼滤波缺乏对噪声的实时估计与信息更新,在精确度上要逊色于变分贝叶斯容积卡尔曼滤波。
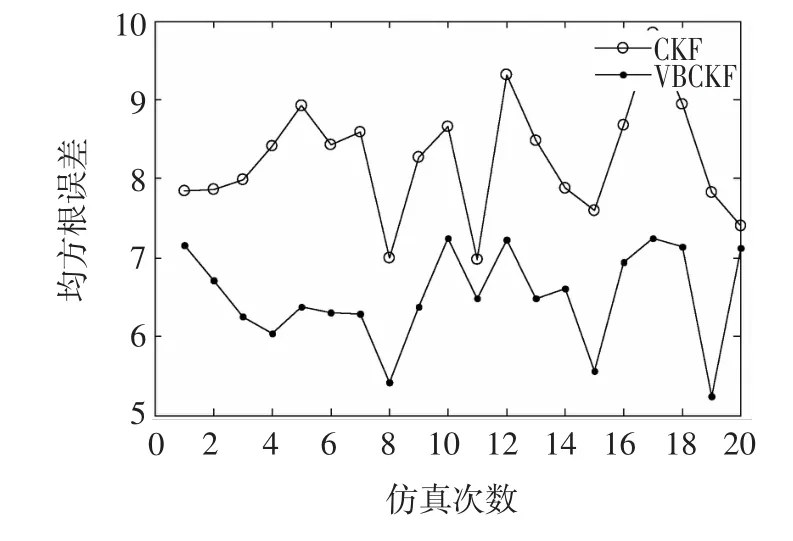
图1 滤波器性能对比Fig.1 Performance com parison between two different filters
图2给出了变分贝叶斯容积卡尔曼滤波器对噪声方差的跟踪情况。从中可以看出,在两次噪声发生剧烈的跳变后,利用变分贝叶斯方法迭代地逼近真实的噪声方差,不仅有着很快的收敛速度,能够较快地给出方差的估计值,而且在估计精确度上也有着较好的表现。对应体现在图1中,相比容积卡尔曼滤波,变分贝叶斯容积卡尔曼滤波器有着更小的误差。
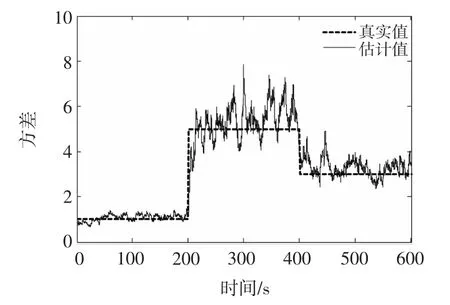
图2 噪声方差跟踪图Fig.2 Tracking of noise variance
5 结 论
针对典型的非线性系统模型,在容积卡尔曼滤波器的基础上结合变分贝叶斯方法,本文提出了一种自适应变分贝叶斯容积卡尔曼滤波方法,该方法对状态量进行更新之前,实时地跟踪观测噪声的方差,使滤波器的参数设计能够尽可能和工作状况相匹配,从而达到自适应滤波的目的,仿真结果验证了本文所提方法的有效性。
[1] S.J.Julier,J.K.Uhlmann,H.F.Durrant-Whyte,A new approach for filtering nonlinear systems[c]//In Proc.1995 American control,conference,Seattle,Washington,1995:1628 -1632.
[2] D.Simon,Optimal state estimation[M].Hoboken,New Jersey: John Wiley&Sons,Inc.,2006:397-407,447-452.
[3] R.Mehra,Approaches to adaptive filtering[J].IEEE Transactions on Automatic control,1972,17(5):693-698.
[4] c.P.Robert and G.casella,Introducing Monte carlo Methods with R[c].Springer,2010:167-175.
[5] D.J.c.MacKay,Developments in probabilistic modelling with neural networks-ensemble learning:in Neural Networks:Artificial Intelligence and Industrial Applications[c]//Proc.3rd Annu. Symposium on Neural Networks,Nijmegen,Netherlands,14-15 Sept.1995.Berlin:Springer,1995:191-198.
[6] H.Attias,Inferring parameters and structure of latent variable models by variational Bayes[c]//In Proc.15th conf.Annu. conf.on Uncertainty in Artificial Intelligence,San Francisco,c A,1999:21-30.
[7] G.chantas,N.Galatsanos,A.Likas.Variational Bayesian image restoration based on a product of t-distributions image prior[J]. IEEE Transactions on Image Processing,2008,17(10):1795 -1805.
[8] A.Honkela,H.Valpola,A.Llin.Blind separation of nonlinear mixtures by variational Bayesian learning[J].Digital Signal Processing,2007,17(5):914-934.
[9] Q.Huang,J.Yang,Y.Zhou,Variational Bayesian method forspeech enhancement[J].Neurocomputing,2007,70(16-18): 3063-3067.
[10] K.Harada,H.Sakai,Variational Bayesian blind estimation of SIMO channels[c]//In Proc.IEEE Int.conf.Acoustics,Speech,and Signal Processing,Dallas,TX,Mar.14-19,2010:3218-3221.
[11] M.D.Vrettas,D.cornford,M.Opper,Estimating parameters in stochastic systems:A variational Bayesian approach[J].Physica D,2011,240(23):1877-1900.
[12] B.Ait-El-Fquih T.Rodet,Variational Bayesian Kalman filtering in dynamical tomography[c]//In Proc.IEEE International conference on Acoustics,Speech,and Signal Processing,Prague,c zech Republic,May 22-27,2011:4004-4007.
[13] S.Sarkka,A.Nummenmaa,Recursive noise adaptive Kalman filtering by variational Bayesian approximations[J].IEEE Transactions on Automatic control,2009,54(3):596-600.
[14] J.Sun,J.Zhou X.Gu,Variational Bayesian two-stage Kalman filter for systemswith unknown inputs[J].Procedia Engineering,2012,29(1):2265-2273.
[15] S.Sun,c.Peng,W.Hou,et al,Blind source separation with time series variational Bayes expectation maximization algorithm[J].Digital Signal Processing,2012,22(1):17-33.
[16] M.Opper and O.Winther,From naïvemean field theory to the tap equations[M].In Advanced Mean Field Methods,M.Opper and D.Saad,Eds.cambridge,MA:MIT Press,2001:7-20.
[17] M.J.Beal,Variational algorithms for approximate Bayesian inference[D].Ph.D.dissertation,Univ.college London,London,2003.
(编辑:刘素菊)
Adaptive variational Bayesian cubature Kalman filtering
SHEN Feng, XU Guang-hui, SANG Jing
(college of Automation,Harbin Engineering University,Harbin 150001,china)
Focusing on the performance of cubature Kalman filteringmay be degraded due to the fact that in practical situations the statistics ofmeasurement noisemight change.An adaptive variational Bayesian cubature Kalman filtering algorithm was proposed which can be used in non-linear system models.In each update step of proposed method,both system state and time-variantmeasurement noise were recognized as random variables to estimate.Measurements noise variances were approximated by variational Bayes,thereafter,system states were updated by cubature Kalman filtering.Simulation results demonstrate the proposed filter can well track measurement noise for a non-linear system and outperforms cubature Kalman filter.
variational Bayes;cubature Kalman filtering;adaptive;non-linear system
10.15938/j.emc.2015.04.015
TP 202
A
1007-449X(2015)04-0094-06
2013-05-29
国家自然科学基金(61102107,61374208);中央高校基本科研业务费专项资金(HEUc FX41310)
沈 锋(1981—),男,副教授,研究方向为非线性滤波技术等;徐广辉(1987—),男,博士研究生,研究方向为自适应信号处理技术等;桑 靖(1988—),女,硕士研究生,研究方向为多传感器信息融合技术等。
沈 锋
