乘用车物流运输计划问题

周建军，张 顺，臧碧莲，林道荣

（1.南京工程学院，江苏 南京 211167；2.南通大学 理学院，江苏 南通 226019）

乘用车物流运输计划问题

周建军1，张 顺2，臧碧莲2，林道荣2

（1.南京工程学院，江苏 南京 211167；2.南通大学 理学院，江苏 南通 226019）

对于整车物流问题，先研究每辆轿运车有效的乘用车各种方案，从装载方案、行车路线、目的地、区分上、下层等角度引入基于运输需求的轿运车数量的决策变量，建立了整数线性规划模型，并利用启发式算法求解了该模型，主要是考虑顺带问题，使总成本较低。

轿运车；乘用车；整车物流；运输计划；整数线性规划模型；启发式算法

1 引言

整车物流指的是按照客户订单对整车快速配送的全过程。近年来，随着我国汽车工业的高速发展和国内整车物流量，特别是乘用车的整车物流量的日益迅速增长[1]，而国内大多数物流公司在制定运输计划时主要依赖于调度人员的经验，在面对复杂的运输任务时，效率低下且运输成本相对较高。因此，乘用车物流运输优化问题已经成为物流领域研究的热点问题，受到了诸多学者的关注[2]。物流公司在确保完成乘用车生产厂家所下达的任务的前提下，制定科学、有效且详细的运输计划十分必要，从而实现物流成本的最小化，提高整车物流的工作效率，推动社会经济的迅速发展[3]。

本文通过研究整车物流的运输规划问题，经过问题分析可知，要用经典的运输问题线性规划模型来描述整车物流并不可行，由于运输问题的宗旨是运价或运输成本最低，而运价或运输成本是所派轿运车辆数的线性函数，故可通过建立线性规划模型求解，通过实际应用，验证了模型的可行性。

2 模型的建立

2.1 问题分析

乘用车物流运输规划问题是一类运输方案，而对于平衡运输问题，可以建立线性规划模型利用表上作业法解决[4]。对于整车物流运输问题，其宗旨是运价或运输成本最低，而运价或运输成本是所派轿运车辆数的线性函数（系数为运输距离与所行里程运价），可以想象此问题可以建立线性规划模型进行求解。作为线性规划问题有三大要素：一是确定合理的决策变量，二是目标函数，三是给出约束条件[5]。

对于乘用车物流问题，可考虑轿运车装载乘用车，并且可双层装载，由于车辆长度限制，应保证乘用车前后、左右的间距为0.1m，轿运车有上、下两层，可用Q表示轿运车的类型量，q表示第q型轿运车的上层，q=1,2,...,Q，Q+q表示第q型轿运车的下层，Mq表示第q型轿运车的拥有量。对于乘用车，可用L表示乘用车的类型量，l为乘用车的类型序号，表示第l型乘用车，l=1,2,...,L。由于轿运车上下层的装载方式不同，用nq表示第q型轿运车上层充分装载乘用车的方案数，nQ+q表示第Q+q型轿运车下层充分装载乘用车的方案数。用

表示对于第q型轿运车的上层采用第i种装载方式装载的第l型乘用车的数量，两列时保持两侧对称，表示对于第q型轿运车的下层采用第i种装载方式装载的第l型乘用车的数量，两列时保持两侧对称。引入的决策变量是数值本身应当是基于运输需求的轿运车的数量。

整车物流的运输成本计算较为复杂，可以这样简化：与轿运车使用量x成正比，与行驶里程hq(q =1,2,...,Q )成正比，与轿运车车型有关，引入运价系数Kq(q=1,2,...,Q)来解决，这样x辆第q型轿运车行驶里程hq(q =1,2,...,Q )的运输成本表示为Kqhqx。在此基础上对运输路线累加，再对轿运车车型累加即得总成本。

对于约束条件，由于轿运车有上下两层，因此为了充分利用轿运车的上下两层，必须考虑在一定条运输路线上，同一种轿运车的上层数量是应当等于下层数量，这理解为平行约束，并且限制条件要注意各轿运车的使用量要分别小于运载乘用车所需的轿运车的数量。约束最重要的是需求约束，注意到目的地有两类，一类是终点性目的地，另一类是中转型目的地。用 Z表示目的地的总数，z表示第 z个目的地，z=1,2,...,Z。对于目的地需求量，用Pil表示第i个目的地对第l型乘用车的总需求量或起点的待运量。Plz表示第z个目的地对第l型乘用车的需求量。对于终点性目的地的，到达这一终点性目的地的各种类型乘用车的运输是分别不小于该目的地各种类型乘用车的需求量；而对于中转型目的地，应考虑经过这一中转性目的地运输路线上的其他目的地远离起点的方向，所有到达这些目的地的各种类型的乘用车的运数量之和分别不小于这些目的地各种类型乘用车的需求量。

2.2 轿运车的可装载方案

每辆轿运车装载乘用车是有效装载。所谓有效的乘用车装载方案是指：一是一层双列排时需左右对称装载乘用车；二是一列尽可能轿运车，直到未能装载为止，或有车位限制时，每个车位装载一辆乘用车，车位位置可前后适当调整；三是装载乘用车时保证乘用车前后、左右的间距（规定0.1m）。

对于每辆轿运车的装载可构建模型如下：若整个装载过程分为M步，规定轿运车最大载重量为G，整个轿运车的装载空间为V(X ,Y,Z)，其中X表示长，Y表示宽，Z表示z轴方向的长度。如果有n种乘用车，数量依次为l1,l2,∙∙∙,ln，每个乘用车的体积为vj(j=1,2,∙∙∙,n)，可用vj(xj,yj,zj)表示第 j种型号的箱子的体积，其中 xj,yj,zj(j =1,2,∙∙∙,n )分别表示长、宽、高，重量为gj(j=1,2,∙∙∙,n)，lij表示第i步装入第 j种型号乘用车的个数，Li为第i步装载后n种型号乘用车摆放乘用车的总数量。可构建只有约束条件没有目标函数的可装载方式模型：

约束条件为：

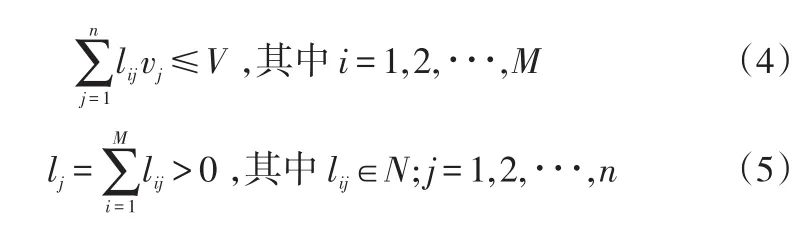
对于上述建立的模型，由于没有目标函数，只有约束条件，可利用LINGO软件进行求解。LINGO软件可以解决只有约束条件，没有目标函数的组合（规划）问题。

2.3 轿运车的派发

2.3.1 一般优化模型形式。对于决策变量：如果从起点到每一个目的地只有单一运输路线，表示对第z个目的地的需求量，在轿运车上层选用第 j种装载方式装载乘用车所需第q型轿运车的数量，其中q=1,2,...,Q;z=1,2,...,Z;j=1,2,...,nQ+q；+q表示对第z个目的地的需求量，在轿运车下层选用第 j种装载方式装载乘用车所需第q型轿运车的数量。

如果从起点到一些目的地有多种运输路线，这样的目的地记为 A1,A2,...,Az0，这里1≤z≤Z0对于目的地Az(1 ≤z≤Z0)，假设有Kz条路线，表示对第z个目的地的部分需求量，在从起点O到目的地Az的第s条路线上，在轿运车上层选用第 j种装载方式装载乘用车所需第q型轿运车的数量，其中q=1,2,...,Q;z=1,2,...,Z;j=1,2,...,nQ+q;s=1,2,...,OKz。+q,s表示对第z个目的地的部分需求量，在从起点O到目的地Az的第s条路线上，在轿运车下层选用第 j种装载方式装载乘用车所需第q型轿运车的数量。如果Z0=Z，那么从起点到每一个目的地都有多条运输行车路线，此时Kz＞1,z=1,2,...,Z；如果Z0=0，那么从起点到每一个目的地都有一条运输路线，此时 Kz=1,z=1,2,...,Z ；如果 0＜Z0＜Z ，那 么从起点到A1,A2,...,Az0目的地都有多条运输路线，其余Z-Z0个目的地均只 有 一 条 运 输 路 线 ，此 时 K1＞1,K2＞1,...,Kz0＞1, Kz0+1=,...,=KZ=1，这样采用假设从起点到目的地Az有Kz条运输路线，Kz≥1,z=1,2,...,Z。表示从起点O到目的地Az的第s条运输路线所派的第q型轿运车的数量，z=1,2,...,Z;s=1,2,...,Kz;q=1,2,...,Q ，显 然

对于目标函数，hzs表示从起点O到目的地Az的第s条运输路线的距离，s=1,2,...,Kz;z=1,2,...,Z；用Kq表示第q型轿运车的距离运价系数，即从起点O到目的地Az的运输里程成本：

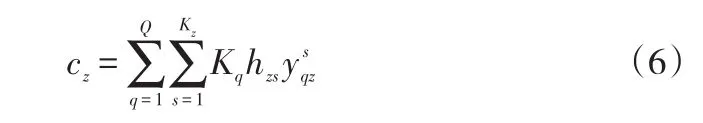
由此可得起点O到所有目的地的运输里程总成本：

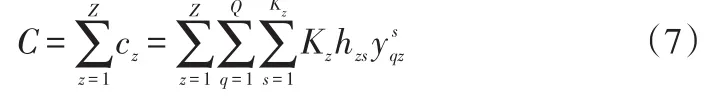
对于约束条件，上下层平衡约束:

需求约束：把目的地分为两类，一类是终点性目的地，记为{B1,B2,...,Bu}，另一类是中转性目的地记为{G1,G2,...,Gv}，显然1＜u,v＜Z，且u+v=Z。

（1）终点性目的地约束。zt表示终点目的地的Bt目的地序号，1≤zt≤Z,t=1,2,...,u。

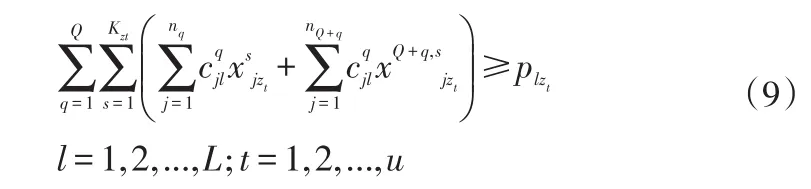
（2）中转性目的地需求约束。对于中转性目的地Gw(w =1,2,...,v) ， 目 的 地 序 号 用 zw表 示 ，1≤zw≤Z,w=1,2,...,v，用c1,c2,...,chw表示运输路线经过的目的地，目的地序号依次用zα1,zα2,...,zαhw表示。

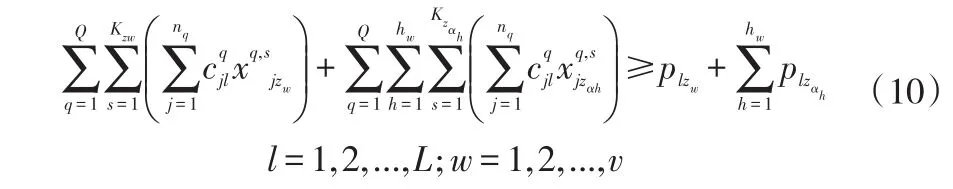
变量关系约束:

变量数值约束:

使用量约束限制:

综上所述，可得到一般优化模型形式，即以式（7）表示的目标函数为最小，式（8）-式（14）为约束的整数线性规划模型。2.3.2 模型求解算法。对于建立的一般优化模型，可采用启发式算法来求解。算法求解步骤如下：

Step1：输入轿运车规格（长、宽、高）及拥有量、轿运车型号数、乘运车规格（长、宽、高）、乘运车型号数、目的地乘运车各型号需求量、目的地数目、起点到目的地的运输路线数目、起点到目的地各运输路线的距离、轿运车单位里程运价系数、目的地序号、终点性目的地集合与序号、中转性目的地与序号等数据。

Step2：确定终点性目的地的运输方案。

（1）针对此目的地的需求量，确定轿运车车型及轿运车装载乘运车的有效装载方案，并对一层的各有效装载方案按最优、次优....最差进行优劣排序；

（2）按一层的最优装载方案选择第一种型号的若干轿运车辆装载乘运车，直到用这种轿运车正好装完结束；否则，剩余乘运车一辆轿运车装完转（3），剩余乘运车不能装满一轿运车转（4），记录所用第一种型号的轿运车的数量与装载情况；

（3）按一层的非最优装载方案选择第一种型号的若干轿运车辆装载乘运车，直到用这种轿运车正好装完；否则，剩余的乘运车不能装满一轿运车，转（4），记录并累加所用第一种型号的轿运车的数量与装载情况；

（4）调整：减少一辆装满乘运车的第一种型号的轿运车，其所装载乘运车连同之前剩余乘运车选择第二种型号的轿运车。如果用1辆第二种基本能装载完乘运车（轿运车上允许有空车位，但很少），结束；否则，再减少一辆装载乘运车的轿运车，两辆轿运车所装载的乘运车连同之前剩余乘运车选择第二种型号轿运车。如果用两辆第二种型号的轿运车基本能装载完乘运车（轿运车上允许有空车位，但很少），结束；否则继续调整，记录并累计所用各种型号轿运车的数量与装载方式。

Step3：确定中转性目的地的运输方案。

（1）同Step2（1）；

（2）同Step2（2）；

（3）同Step2（3）；

（4）对剩余不能装满一轿运车的乘运车向经过此中转性目的地的其它目的地的轿运车进行添加装载，如果能添加装载完剩余乘运车，结束；否则转（5）。记录轿运车型号、数量与装载方式；

（5）调整：减少一辆装满乘运车的第一种型号的轿运车，其所装载乘运车连同之前剩余乘运车选择第二种型号的轿运车，先考虑向经过此中转性目的地的其它目的地的轿运车进行添加装载，如果用1辆第二种型号的轿运车基本能装载完乘运车，结束；否则，继续调整（对经过此目的地的第一种轿运车可以减少地调整）。

Step4：轿运车运输路线确定与成本计算。确定直达目的地的轿运车型号、数量及运输路线距离，计算成本。确定非直达目的地的轿运车型号、数量，停留下载地点与下载乘运车型号、数量及运输路线距离，计算成本，并累加成本。

Step5：记录可行解与总成本。

Step6：可行解改进最优。

（1）多运输路线目的地车辆调整，运输路线距离长的线路减少运价系数高的并增加运价系数低的轿运车；运输路线距离短的线路减少运价系数低的并且增加运价系数高的轿运车，计算总成本，如减少继续调整，否则转（2）；

（2）离起点远的目的地轿运车尽可能选用运价系数低的轿运车，离起点近的目的地轿运车尽可能选用运价系数高的轿运车。计算总成本，如减少，继续调整；否则停止调整，以调整前的可行解作为较优的解，结束。

2.4 模型举例及推广

若某物流公司要运输166辆I车型的乘用车（其中目的地A、B、C、D分别为42、50、33、41辆）和78辆II车型的乘用车（其中目的地A、C分别为31、47辆），具体路线如图1所示，1-1型及2-2型轿运车上、下层装载区域相同，可装载一列；1-2型轿运车上、下层装载区域长度相同，但上层比下层宽0.8m，上层装载两列，下层装载一列，为方便后续任务安排，每次1-2型轿运车使用量不超过1-1型轿运车使用量的20%；各段长度：OD=160，DC=76，DA=200，DB=120，BE=104，AE=60。具体数据见表1-表3。请为物流公司安排运输，制定详细计划，含所需要各种类型轿运车的数量、每辆轿运车的乘用车装载方案。

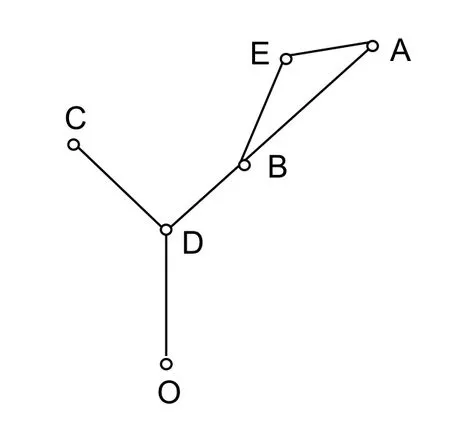
图1 各个目的地分布状况

表1 乘用车的规格

表2 轿运车的规格

表3 轿运车的运价系数（km/元）

利用模型启发式算法并结合LINGO求解软件可得到，总运价为3 376元，OD段需要1-1型轿运车15辆，1-2型轿运车7辆，每辆车的装载情况见表4。

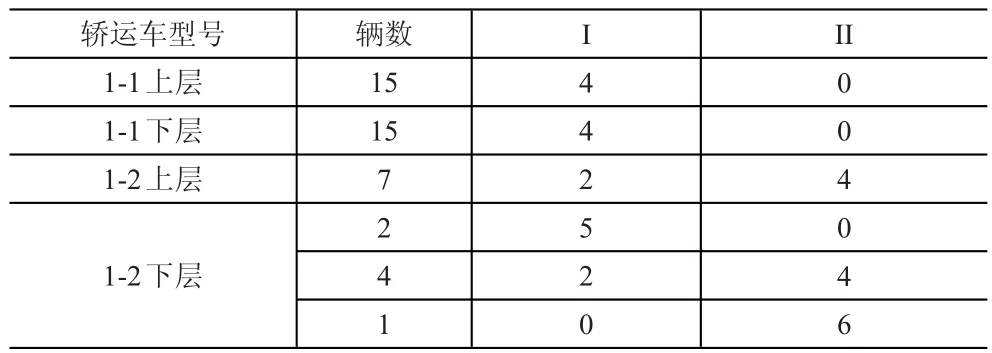
表4 OD段车辆装载情况

DC段需要1-1型轿运车5辆，1-2型轿运车2辆，每辆车的装载情况见表5。

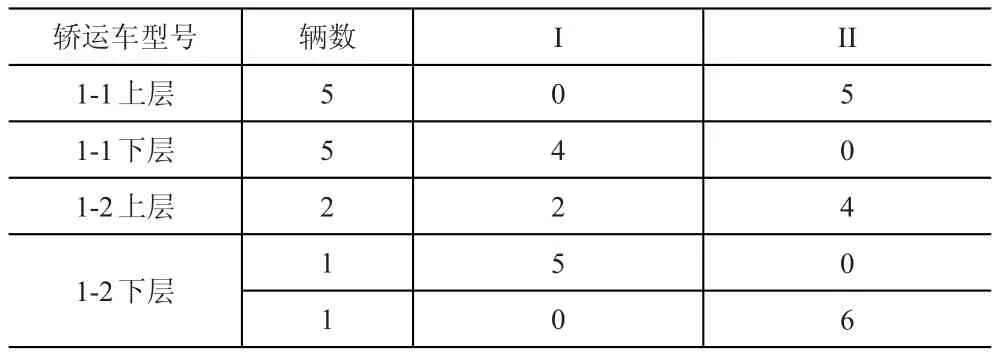
表5 DC段车辆装载情况

DB段需要1-1型轿运车10辆，1-2型轿运车3辆，每辆车的装载情况见表6。

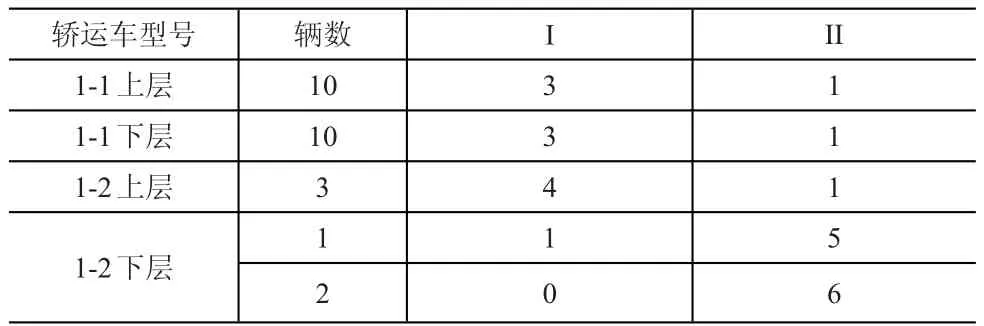
表6 DB段车辆装载情况

BA段需要1-1型轿运车5辆，1-2型轿运车2辆，每辆车的装载情况见表7。

表7 BA段车辆装载情况

[1]韩龙士.供应链管理下的汽车物流研究[J].汽车工业研究,2006,(6):8-9.

[2]杨海荣.现代物流系统与管理[M].北京:北京邮电大学出版社,2003.

[3]王占锋,张翠军.求解非满载车辆调度问题的改进遗传算法[J].计算机工程与设计,2008,29(15):3 991-3 993.

[4]胡富昌.线性规划(第二版)[M].北京:中国人民大学出版社,1990.

[5]姜启源,谢金星,叶俊.数学模型(第三版)[M].北京:高等教育出版社, 2008.

Study on Problems in Passenger Vehicle Logistics and Transportation Solutions

Zhou Jianjun1,Zhang Shun2,Zang Bilian2,Lin Daorong2
(1.Nanjing Institute of Technology,Nanjing 211167;2.School of Science,Nantong University,Nantong 226019,China)

In this paper,we first analyzed some effective passenger vehicle transportation solutions,then from the angles of loading, route,destination and stacking,etc.,introduced in the decision-making variables concerning the quantity of the car carriers,built the corresponding integer linear programming model and at the end,used a heuristic algorithm to solve it.

car carrier;passenger vehicle;vehicle logistics;transportation plan;integer linear programming model;heuristic algorithm

F426.471；F252

A

1005-152X(2015)10-0123-04

2015-07-11

周建军（1968-），男，江苏如皋人，讲师，博士在读，研究方向：系统工程；张顺（1990-），女，山东单县人，研究生，研究方向：运筹与控制；臧碧莲（1992-），女，江苏靖江人，研究生，研究方向：组合设计理论；林道荣（1963-），通讯作者，男，江苏海安人，教授，研究方向：组合优化。

10.3969/j.issn.1005-152X.2015.10.034