基于支持向量机回归的协同过滤相似度优化方法

吕成戍，盖 印，匡宇鹏

（1.东北财经大学 管理科学与工程学院，辽宁 大连 116025

2.内蒙古中电物流路港有限责任公司赤峰铁路分公司，内蒙古赤峰 024000）

基于支持向量机回归的协同过滤相似度优化方法

吕成戍1，盖 印1，匡宇鹏2

（1.东北财经大学 管理科学与工程学院，辽宁 大连 116025

2.内蒙古中电物流路港有限责任公司赤峰铁路分公司，内蒙古赤峰 024000）

在基于属性相似性的协同过滤算法中，项目属性之间相似性的度量是整个算法的关键。现有算法在计算项目属性相似度时忽略了项目属性之间的非线性关系，导致相似性度量不准确，无法保证项目推荐精度。针对这一问题，本文提出一种基于支持向量机回归的协同过滤相似度优化方法，该方法利用支持向量机回归算法来构建项目属性相似度模型，解决项目属性的非线性关联问题，改善项目属性相似度计算。实验结果表明，优化方法计算出的项目相似性更准确，显著提高了系统的推荐质量。

支持向量机回归；项目属性相似性；协同过滤

0 引 言

协同过滤推荐是当前最成功的推荐技术之一[1]，根据过滤操作对象的不同，协同过滤算法可以分为基于用户(User-based)[2]和基于项目(Item-based)[3]的算法。User-based协同过滤算法随着数据的不断增多，要从大量用户中寻找最近邻居用户的问题成为推荐系统发展的瓶颈，而Item-based协同过滤算法通过将计算用户之间的相似性转换为计算项之间的相似性的方法，有效地解决了这一问题。在Item-Based协同过滤算法中，项目之间相似性的度量是否准确，直接关系到整个推荐系统的推荐质量。而实际上，由于系统用户评分数据的极端稀疏性，传统的相似性度量方法存在着一定的弊端，系统的推荐精度往往会很低。为了提高系统推荐精度，一些研究者们对项目相似性计算方法进行了改进。根据项目属性相似度和用户评价相似度，计算项目之间的综合相似度，但项目属性相似度的计算公式只简单考虑两个项目间相同的属性数，未考虑项目属性的重要性差异。因此将项目属性相似度和项目评分相似度的线性组合作为最终邻居相似度，在计算项目属性向量的相似度时，使用加权计算来解决项目属性的重要性差异问题。以上算法的核心就是用基于项目属性的相似性来改进传统Item-Based协同过滤中目标项目的最近邻居项目集的查找，项目属性相似度的计算是这类改进方法的关键。但是，目前基于属性相似性的Item-Based协同过滤算法将项目属性之间的复杂关系进行了简单的线性化处理,忽略了项目属性的非线性关系，在一定程度上影响了算法的效能。

Vapnik等人根据统计学习理论提出的支持向量机（Support Vector Machine,SVM）[7]方法具有诸多的优良特性，近年来引起了广泛的关注，SVM方法最早是针对模式识别问题提出的，Vapnik通过引入不敏感损失函数，得到了用于回归估计的SVM方法，称为支持向量机回归(Support Vector Regression，SVR)[8]，SVR方法被引入非线性回归领域，显示了其巨大威力[9，10]。本文利用支持向量机回归算法的回归能力，解决项目属性的非线性关联问题。实验结果表明，本文所提的算法大幅提高了推荐算法的精确度。

1 支持向量机回归

一般的回归问题可表述为：给定l个训练样本，学习机从中学习出输入、输出变量之间的关系(依赖关系、映射关系、函数关系)f(x)。考虑一个训练样本数据集{(x1，y1)，…，（xl，yl）}。对于i=1，…，l其中xi∈Rn每个代表了样本的输入空间，存在一个目标值yi∈R与其相对应。回归问题的思想就是从中学习出一个函数，能够精确地估计未来值。一般的SVR函数形式为：

其中，w∈Rn，b∈R，Φ代表了从Rn到高维空间的一个非线性变换。我们的目标是找出w和b的值，使回归风险函数最小化。回归风险函数为：

其中，Γ(·)是损失函数，常数C＞0，表示对估计偏差的惩罚度。最常用的损失函数是Vapnik提出的ε-敏感度函数。解决回归问题时，SVM是在n维特征空间中，使用ε-敏感度损失函数来求解一个线性回归问题。同时，它要通过最小化‖w‖2来减小模型容量，以保证更好地拟合一般性。于是我们得到了Vapnik所描述的最优化问题：

其中，ξi，ξ*i是代表输出结果上下界的松弛变量。

经过推导，可得到其对偶优化问题为：

在解出以上的二次优化问题后，一般公式可以改写为：

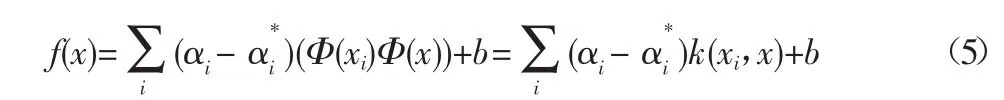
在公式(5)中，点积可以用核函数k(xi，x)来代替。核函数能够在不知道变换具体函数的情况下，使用低维空间的数据输入来计算高维特征空间中的点积。通常使用的核函数包括线性函数、多项式函数以及RBF等。

2 基于支持向量机回归的相似度优化方法

2.1 项目的特征属性

一般来说，推荐系统至少存在3个基本数据表，一个用来记录注册用户信息，一个用来记录项目信息，还有一个记录用户的评分信息(记为用户评分表)。通过对记录项目信息表的整理可以得到项目特征属性矩阵A。假定接受评分的项目数是n，每个项目挑选k个具有代表性的属性描述，在此将其抽象为 {Attr1，Attr2，…，Attrk}。见表1，项目属性矩阵A(其中1表示某个项目具有某项属性，0表示某个项目不具有某项属性)，项目特征属性的抽取可以从项目的简介网页中提取，或者从推荐系统中用来记录项目信息的表中整理得到。

表1 项目属性矩阵A

2.2 构建项目属性相似度模型

设任意两个项目Itemx、Itemy在k维项目特征属性空间上的属性值分别看做向量Itemx={Attrx,1，Attrx,2，…，Attrx,k}和Itemy={Attry,1，Attry,2，…，Attry,k}，并且该向量元素的取值为二维数据(0或1)，则项目Itemx和项目Itemy之间的属性相似性simAttr(Itemx，Itemy)的计算公式为[6]：

其中simAttr(Itemx，Itemy)为两个物品的相似度，sim(Attrj(Itemx)，Attrj(Itemy))则是Itemx，Itemy关于属性Attrj的相似度。wj是根据经验对每个属性Attrj赋予一个权值，且相似度是对每种特征进行线形加权，但是对于非线性相似度则会出现较大的误差。例如用户可能会觉得只要是导演A与演员B合作的影片，无论风格以及年代的差距有多大，都是非常相似的。针对这个问题，本文使用支持向量机的方法来解决。两个物品在项目属性上的相似度修改为：

在构建回归模型时，线性回归模型难以拟合复杂的项目属性相似度，并不能得到好的回归效果。如上所述，支持向量机回归（SVR）能够通过核函数，将只包含上述自变量的低维空间，转化为一个包含了它们非线性组合的高维自变量空间。于是本文引入SVR方法来构建此非线性回归模型。基于公式（5），可构建模型如下：

为了提高算法执行效率，本文使用序贯最小优化（Sequential Minimal Optimization，SMO）方法[10]，一种快速支持向量机训练算法来求解此模型。

2.3 优化后的推荐算法

SVR相似度优化方法仅仅是针对基于属性相似性的Item-Based协同过滤算法提出的一种新的计算项目属性之间相似性的方法，因此只需要将基于属性相似性的Item-Based协同过滤算法中的项目属性相似性度量方法转换为SVR相似度优化方法，就可以得到一种新的基于属性相似性的Item-Based协同过滤推荐算法，称之为基于SVR的协同过滤推荐算法，简称SVRBased CF。

算法1 基于SVR的协同过滤推荐算法

输入：用户—项目评分矩阵R，项目属性矩阵A，最近邻居个数k，推荐集元素个数r，项目相似性平衡参数α。

输出：推荐集rec。

（1）基于用户—项目评分矩阵R，采用相关相似性计算项目i和项目j之间的评分相似性simRate(i，j)。

（2）基于项目属性矩阵A，按式(4)计算任意两个项目间的属性相似性simAttr(i，j)，并建立项目属性相似性矩阵simAttr(i，j)。

（3）将simRate(i，j)与simAttr(i，j)进行线性组合，计算最终的项目相似性矩阵sim(sim为n×n方阵，其元素的值以主对角线为轴对称分布，即sim(i，j)=sim(j，i)，如下所示：

（4）搜索项目相似性矩阵sim将相似度最高的若干项目作为目标项目l的邻居集合Nl={i1,i2，…，ir}，并且l埸Nl

（5）根据相似邻居预测用户u对未评分项目l的评分，公式如下：

其中，Nl是项目l的邻居集合，与指项目l和p的平均评分。

（6）对用户u未评价过的项目预测评分从大到小进行排序，取前r个值对应的项组成推荐集rec={i1,i2，…，ir}进行推荐。

3 实验及分析

3.1 数据集

数据集取自MovieLens数据集[11]，该数据集由明尼苏达大学GroupLens研究小组通过MovieLens网站（http://movielens.umn.edu）收集，包含了943位用户对1 682部电影的100 000条评分数据，每位用户至少对20部电影进行了评分，所有电影分属于19种电影类别。为了分析实验数据稀疏性对算法性能的影响，本文从MovieLens数据集上随机抽取100、200、300位用户的评分数据组成3个数据集，分别记为TDS100、TDS200、TDS300。

3.2 评价标准

评价推荐系统推荐质量的度量标准采用统计度量方法中的平均绝对偏差MAE(Mean Absolute Error)进行度量。MAE通过计算预测的用户评分与实际的用户评分之间的偏差来度量预测的准确性，MAE越小，推荐质量越高。

3.3 实验结果及分析

实验以传统Item-based协同过滤(Item-based CF)、基于属性相似性的Item-based协同过滤(Item feature-based CF)[3]以及基于属性线性加权的Item-based协同过滤 (Item feature weightedbased CF)[4]为对照，检验本文提出的算法的有效性，计算各种推荐算法的MAE。实验中最近邻居个数k取30,推荐集元素个数r取10，项目相似性平衡参数α取0.6，实验结果见表2。

表2 MAE对比结果

由表2可知，Item feature-based CF方法优于Item-based CF方法，说明在计算项目相似性的过程中考虑项目属性相似性,可以有效改善传统协同过滤算法中面临的“稀疏性”问题,提高推荐算法的推荐质量。Item feature weighted-based CF方法优于Item feature-based CF方法的性能，说明通过加权计算可以解决项目属性重要性不同的问题，能有效改善推荐方法的性能，而本文提出的方法的MAE值较Item feature weighted-based CF方法的MAE值有大幅度的降低，说明加入支持向量机后明显优于线性组合的特征加权，通过支持向量机回归方法改善项目属性相似性的计算，能使得项目的相似性计算更加准确，进一步提高方法的性能。

4 结束语

本文提出了一种基于支持向量机回归的协同过滤相似度优化方法，该方法在计算项目属性相似性时考虑了项目属性之间的非线性关联问题,使得项目属性的计算更加合理。实验结果表明,本文提出的优化方法能够获得更准确的项目相似性,在一定程度上提高了系统的推荐质量。

[1]D Goldberg,D Nichols,B M Oki,et al.Using Collaborative Filtering to Weave an Information Tapestry[J].Communications of the ACM,1992,35 (12):61-70.

[2]P Resnick,N Iacovou,M Suchak,et al.GroupLens:An Open Architecture for Collaborative Filtering of Netnews[C].Proc.of the ACM CSCW′94 Conference on Computer Supported Cooperative Work,ACM,1994：175-186.

[3]B Sarwar,G Karypis,J Konstan,et al.Item-based Collaborative Filtering Recommendation Algorithms[C]//Proceedings of the 10th International World Wide Web Conference,2001.

[4]彭玉，程小平．基于属性相似性的Item-based协同过滤算法［J］．计算机工程与应用，2007，43(14):144-147．

[5]庄永龙．基于项目特征模型的协同过滤推荐算法［J］．计算机应用与软件，2009，26(5):244-246．

[6]张忠平，郭献丽．一种优化的基于项目评分预测的协同过滤推荐算法［J］．计算机应用研究，2008，25(9):2659-2683．

[7]V N Vapnik.Statistical Learning Theory[M].NeuYork,NY:Wiley,1998:35-53.

[8]V Vapnik.An Overview of Statistical Learning Theory[J].IEEE Transactions on Neural Networks,1999,10(5):988-999.

[9]Smola,Scholkopf.Learning with Kernels[M].Cambridge,MA:MIT Press, 2002.

[10]Smola,Scholkopf.A Tutorial on Support Vector Regression[J].Statistics and Computing,2004(14):199-222.

[10]Miller B N，Albert I，et al.Movie Lens Unplugged:Experiences with an Occasionally Connected Recommender System[C]//Proceedings of the International Conference on Intelligent User Interfaces,2003.

10.3969/j.issn.1673-0194.2015.05.109

TP311

A

1673-0194（2015）05-0227-04

2014-12-26

教育部基金项目（14YJC630036）；中央高校专项科研基金项目（DUFE2014126）。