基于流固耦合的混流式水轮机转轮强度分析

阚　阚，郑　源，赵连辉，乔　木，张　策，尉青连（.河海大学水利水电学院，江苏 南京 20098；2.河海大学水资源高效利用与工程安全国家工程研究中心，江苏 南京20098；3.河海大学能源与电气学院，江苏 南京 200；.国网新源控股有限公司白山发电厂，吉林 32000）

基于流固耦合的混流式水轮机转轮强度分析

阚阚1，郑源2，3，赵连辉4，乔木4，张策4，尉青连4
（1.河海大学水利水电学院，江苏 南京 210098；2.河海大学水资源高效利用与工程安全国家工程研究中心，江苏 南京210098；3.河海大学能源与电气学院，江苏 南京 211100；4.国网新源控股有限公司白山发电厂，吉林 132000）

摘要：对我国东北某大型混流式水轮机在设计水头不同工况的转轮强度进行了单向流固耦合计算，采用CFD软件CFX，计算得到各工况流场中叶片表面的水压力，借助ansysworkbench平台，将其作为结构面载荷加载到叶片上，得到各工况下转轮的静应力分布及变形情况。研究结果表明：转轮静应力最大值随着流量的升高而增大，且均出现在叶片出水边连接上冠位置附近；转轮最大变形量随着流量的升高而增大，最大变形量出现在下环位置。研究结果为混流式水轮机结构设计及安全运行提供了有效依据。

关键词：混流式水轮机；流固耦合；静应力；强度分析

1　引言

近年来，国内外一系列水力机组频繁发生振动和转轮叶片裂纹问题，严重影响了机组的安全稳定运行和经济效益。随着流固耦合技术的飞速发展，很多学者对水力机械进行了基于流固耦合的应力特性研究。肖若富等[1-2]对混流式水轮机全流道流场进行了CFD计算，采用顺序流固耦合方法得到了转轮最大静应力与水轮机功率的线性关系。张新[3]等运用单向流固耦合的方法对轴流泵叶轮强度进行分析。利用单向流固耦合方法计算旋转机械应力和变形的有效性和准确性已获得了工程界的认可[1-4]。

本文借助计算流体动力学软件CFX和ansys workbench平台，对我国东北某大型混流式水轮机全流道设计水头下不同工况进行了CFD计算。基于单向流固耦合方法计算得到不同工况下转轮最大静应力和变形量，从而实现对水轮机转轮强度的校核与预测，可对混流式水轮机结构设计优化和裂纹原因分析提供参考。

2　流场计算

2.1计算模型

本文以我国东北某大型混流式水轮机为研究对象，建立了从蜗壳进口至尾水管出口的全流道计算模型（如图1）。转轮型号为HL-200-LJ-550，转轮直径5.5m，设计水头Hd=112m，设计流量Qd=307m3/s，额定转速nd=125 r/min，转轮叶片数z=14，固定导叶数z0=12，活动导叶数z1=24。选取了设计水头下，流量为0.88Qd、Qd、1.15Qd的三种工况进行计算。流体和实体部分均采用UG建模。

图1　混流式水轮机几何模型

2.2计算方法

流体机械内部水流运动可以采用连续性方程和雷诺时均N－S方程联立来描述[5]：

连续性方程：

N-S方程：

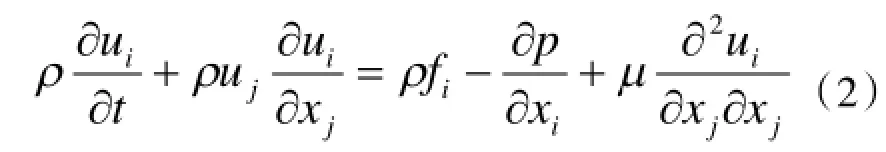
式中，u为流体速度矢量；ρ为流体密度；f为质量力；P为压强；μ为湍动粘度。

一般认为水流是不可压缩流体，不考虑能量守恒方程[6]。通过雷诺时均N-S方程描述湍流运动时，需要引入湍流模型来封闭方程组，本文采用能够准确模拟近壁面区域的SST k-ω模型[7]进行计算域流动特性的模拟。

采用有限体积法对控制方程组进行离散，扩散项和压力梯度采用有限元函数表示，对流项采用高阶求解格式。采用全隐式多重网格耦合方法对流场进行求解，将动量方程和连续性方程耦合求解。

2.3网格划分

流体域包括蜗壳段、座环段、转轮段和尾水管段，结构域只考虑转轮。混流式水轮机全流道过流部件多，几何形状复杂，运用ICEM对流体区域进行几何适应性强的四面体非结构化网格划分，分别对蜗壳、座环、转轮、尾水管进行了网格划分及局部加密，部分流体计算区域网格如图2所示，整个水轮机流体计算域网格单元总数为319.6万，蜗壳、座环、转轮、尾水管网格单元数分别为30.6万，97.8万，167.4万，23.8万。

图2　部分流体计算区域网格

2.4边界条件

在CFX软件平台上完成数值模拟工作，边界条件为：流场进口处设置给定总压边界条件，出口处设置自由出流边界条件，固壁上采用绝热、无滑移边界条件，转轮流体域与转轮实体相接部分定义为流固耦合边界，采用“Frozen rotor”[8]处理转轮与座环、尾水管之间旋转坐标系与静止坐标系流动参数的转换。

2.5计算结果

计算得到三种工况下叶片表面水压力的分布，作为转轮强度有限元计算的流固耦合表面荷载边界条件。以设计工况为例，叶片表面静压分布见图3。

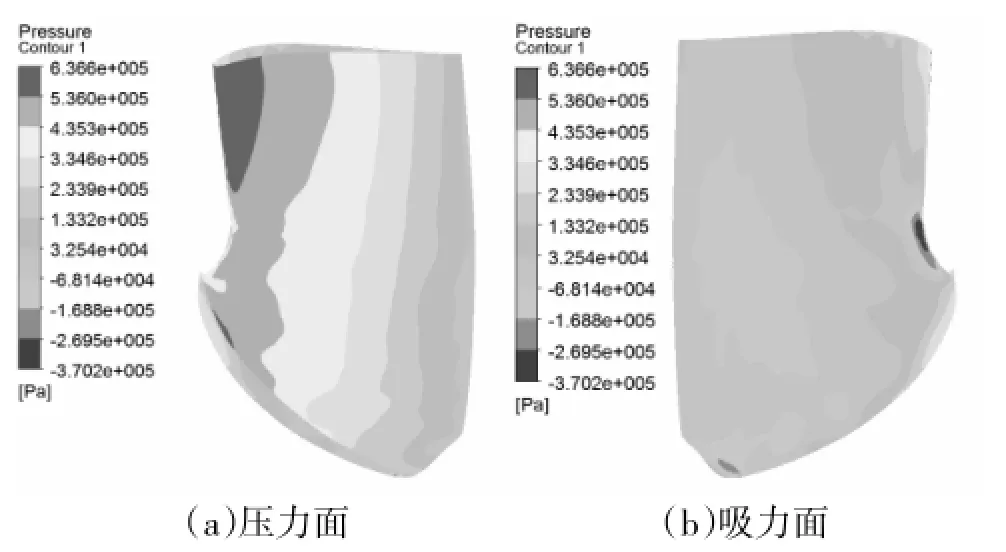
图3　压力面及吸力面静压分布

3　结构场计算

3.1转轮强度计算方法

转轮强度计算的有限元方程如下：

根据第四强度理论结合上式所得的计算等效应力[10]：

式中，σ1、σ2、σ3分别为三个主应力值。

3.2结构模型与边界条件

结构计算的对象为该混流式水轮机转轮。转轮的材料为ZG20SiMn，密度为7 860 kg/m3，杨氏模量为211GPa，泊松比0.29，屈服强度295MPa。转轮尺寸的单元网格设为80mm，采用自由划分的方法对转轮划分网格，由于应力集中常发生在叶片根部区域[10]，为了保证计算精度，对这一敏感区域进行了网格加密。网格划分共产生1 743812个单元和2 550548个节点，如下页图4所示。

模型边界条件包括结构载荷和约束，两种结构载荷有:①惯性载荷，包括重力加速度和转轮转速；②表面载荷，即由前文流场计算获得的作用在所有流固耦合面上的水压力。为了防止产生刚体位移，转轮约束条件设置为在转轮与主轴把合螺栓处，约束相应节点的自由度。整个转轮荷载和约束的设置如下页图5所示。

图4　转轮网格划分

图5　转轮边界条件

3.3流固耦合计算结果

对转轮在3个工况点下进行有限元求解，得到各个工况下转轮的静应力及位移分布云图。由于各工况下转轮的静应力及总变形分布规律相似，只是数值上有所区别，因此只给出转轮在设计工况下的静应力和变形分布。

设计工况下转轮静应力分布如图6所示。水流流态顺畅，叶片压力面与吸力面压差较大，叶片表面静压梯度明显，应力分布趋于均匀，此时应力集中与应力最大值出现在叶片出水边靠近上冠处。这是因为约束条件设置为在转轮与主轴把合螺栓处，在加载了叶片表面水压力载荷的情况下，叶片靠近固定约束处的弯矩和剪力较大，无法通过弯曲和变形释放应力，同时叶片出水边厚度较薄，刚度和强度不足，所以造成了此处的应力集中与应力最大值，并易产生疲劳破坏。

图6　设计流量工况转轮静应力分布及局部放大图

设计工况转轮的变形分布如图7所示。图3中叶片压力面进水边至出水边压力梯度明显，此时可以把各个叶片看成一组通过下环连接的等效悬梁臂，叶片连接上冠处为近似固定端，下环为自由端。在加载了叶片表面压力载荷的情况下，固定端的弯矩和剪力最大，所以应力最大；自由端的弯矩和剪力最小，所以应力最小，因为固定端与上冠相连，靠近转轮与主轴把合螺栓处的固定约束，所以位移为0；自由端无自由度约束，故下环处的位移最大。

图7　设计流量工况转轮总变形分布

通过对结构进行单向流固耦合计算，得到设计水头下三种计算工况下的静应力和位移分布，最大静应力值和最大位移值如表1所示。可以看出，静应力和变形量的最大值均随着流量的升高而增大。对转轮进行强度校核时，取ZG20SiMn的安全系数nb=3，材料屈服强度为σs=295MPa。许用应力 [σ]=σs/nb=98.3MPa.由此可见此混流式转轮在大部分工况运行时不能满足强度要求，转轮可靠性较低；同时第三种工况下最大静应力值达到269.13MPa，与材料屈服强度较为接近，最大静应力出现位置与实际生产运行中转轮裂纹产生的位置相符，实际运行中要极度避免机组在大流量工况下的运行。

表1　转轮的静应力和位移最大值

4　结论

（1）采用UG建模软件对混流式水轮机转轮所在流道内的所有过流部件进行了实体建模，采用CFD方法对混流式水轮机全流道进行三维数值模拟，得到了叶片表面的水压力，并通过ansys软件将水压力载荷加载到叶片表面，得到了各个工况下转轮的静应力分布及变形情况。

（2）各个工况下，最大位移均发生下环处，叶片出水边与上冠连接处附近均发生应力集中，容易产生疲劳破坏。大流量工况下，转轮静应力最大值较为接近材料的屈服强度，实际运行中要极度避免机组在这些工况下运行。在不影响水轮机性能的前提下，应当对叶片出水边连接上冠处进行适当加厚，并倒圆角。

参考文献：

[1]肖若富，王正伟，罗永要.基于流固耦合的混流式水轮机转轮静应力特性分析［J］.水力发电学报，2007，26(3):14－16.

[2]肖若富，王福军，桂中华.混流式水轮机叶片疲劳裂纹分析及其改进方案［J］.水利学报，2011,41（8）：970－974.

[3]张新，郑源，毛秀丽，等.基于流固耦合的轴流泵叶轮强度分析［J］.水电能源科学，2014,32（7）：137－139，150.

[4]W ang W enquanHe，X iaoqiao,Zhang，Lixiang，et al．Strongly coupled simulation of fluid-structure interaction in a Francis hydroturbine[J]．International Journal for NumericalMethods in Fluids，2009,60(5)：515-538．

[5]王福军.计算流体动力学分析--CFD软件原理与应用［M］.北京：清华大学出版社，2004：119－139．

[6]张亮，何环宇，张学伟，等.垂直轴水轮机单向流固耦合数值研究［J］.华中科技大学学报：自然科学版，2014，42 （5），80－84．

[7]荆丰梅，肖钢，熊志民.潮流能水轮机单向流固耦合计算方法［J］.振动与冲击，2013，32（8）：91－95，104.

[8]王洋，王洪玉，张翔，等.基于流固耦合理论的离心泵冲压焊接叶轮强度分析［J］.农业工程学报，2011，27（3）：131－136.

[9]PengGuangjie，W angZhengwei，YanZongguo，et al．Strength analysis of a large centrifugal dredge pump case[J]. Engineering Failure Analysis,2009,16(1):321-328．

[10]Saeed R A，Galybin A N．Sim plified model of the turbine runnerblade[J]．Engineering Failure Analysis，2009，16（7）：2473－2484.

中图分类号：TK733+.1

文献标识码：A

文章编号：1672-5387（2015）02-0009-04

DOI：10.13599/j.cnki.11-5130.2015.02.003

收稿日期：2014-08-12

基金项目：国家自然科学基金重点项目（51339005）；国网新源控股有限公司科技项目KJ（2013）267号。

作者简介：阚阚（1990-），男，博士研究生，研究方向：水力机械优化设计及运行稳定性流固耦合分析。