水电机组盘车摆度准确计算的最新研究成果

2015-07-28林焕森国家电网公司华中分部湖北武汉430077

水电站机电技术 2015年3期

关键词：盘车摆度计算方法

林焕森（国家电网公司华中分部，湖北武汉 430077）

水电机组盘车摆度准确计算的最新研究成果

林焕森
（国家电网公司华中分部，湖北武汉 430077）

摘要：以图示方法通俗易懂地说明了测定水电机组盘车摆度的原理，揭示了摆度参数的变化规律，对判断盘车质量好坏提出了便捷的检查方法，并介绍了快速准确计算盘车摆度的最新研究成果-四点盘车法。

关键词：水电机组；盘车；摆度；计算方法；四点盘车法

0　前言

在立式水电机组安装或大修中，检查机组主轴轴线，使其垂直偏差度(或称轴线弯折程度)控制在容许范围以内，是一项重要的工作内容。调整好机组轴线，不仅有助于改善导轴承磨损，并可提高机组运行稳定性。在水电厂现场，目前检查机组轴线的常用方法当属盘车，根据盘车求得了机组主轴最大摆度点所在方位及其摆度值，经过计算，就可以对推力头与镜板之间的垫片进行处理，把主轴轴线调整到合格状态。以前，作者曾发表过几篇论文，对水电机组的盘车原理及其摆度值的准确计算问题作过一些探讨[1,2,3]，对于提高机组安装精度，取得了实践效果，并且在非水电机组的一些专业领域也获得应用。现经多年研究和实践，作者对这一问题有一些深入的认识，认为用更直观而简单的方法就可搞清盘车摆度变化规律，还发现，只要在导轴承轴颈或者主轴法兰盘等处设4个依次相隔90°的盘车点就可方便而准确地算出盘车摆度(此法称“四点盘车法”)。现将近年来对有关问题的研究成果汇报如下。

1　盘车过程中导轴承轴颈运动规律的最新研究

如众所知，只要水电机组的主轴轴线稍有一点儿不垂直于推力轴承的摩擦平面（水平面），此轴线在旋转过程中就会形成一个圆锥面的轨迹。我们把主轴轴线围绕机组旋转中心线形成的运动轨迹称为摆度锥面，把此锥面与某导轴承处水平面的交线称为该导轴承的摆度圆，我们设此摆度圆的圆心为P，半径为r。为便于研究，我们在此摆度圆上设8个等分点(每隔45°设一个点），并按顺时针方向把它们依次标记为A、B、C、D、E、F、G、H（见图1）。提请注意的是，这个摆度圆相对于机组的固定部分(如轴承体、上机架、下机架等)是静止不动的。也就是说，我们可把这个摆度圆看作是一个静止的平面坐标参照系，把H-D点的连线定为X轴，把F-B点的连线定为Y轴。此外，我们把摆度圆所在平面与导轴承轴颈柱面在某一时刻的交线称为轴颈圆，考虑到制造厂对导轴颈柱面加工精度和圆度的严格保证，我们可以把此轴颈圆看做是一个理想的圆形，并设其圆心为Q，半径为R。在此轴颈圆上也设8个等分点，称之为盘车点，但按逆时针方向把它们依次标记为0号（也可标为8号）、1号、2号、3号、4号、5号、6号、7号（见图2）。不过，在盘车过程中，此轴颈圆是转动的，既有绕其自身圆心Q点的自转，又有其圆心Q点在摆度圆圆周上绕P点的公转（见图1）。如果在轴颈圆边缘某处装一个固定的百分表，则机组每转一周（或者说，轴颈圆上的各点通过百分表测头一次），轴颈圆就会绕其圆心Q自转一周；与此同时，Q点又会绕P点公转一周，见图2（请注意，图2所示为Q点落在P圆的H点上的情况）。在此，要顺便提示一下R和r大小的概念，图2只是一个示意图，在实际设备上，摆度圆的直径尺寸较少超过2mm，而轴颈圆的直径尺寸可达1000mm以上。在上面已经建立起来的摆度圆P和轴颈圆Q的概念基础上，下面，我们进一步研究一下在盘车过程中P圆与Q圆的相互关系。

图1摆度圆形成示意图

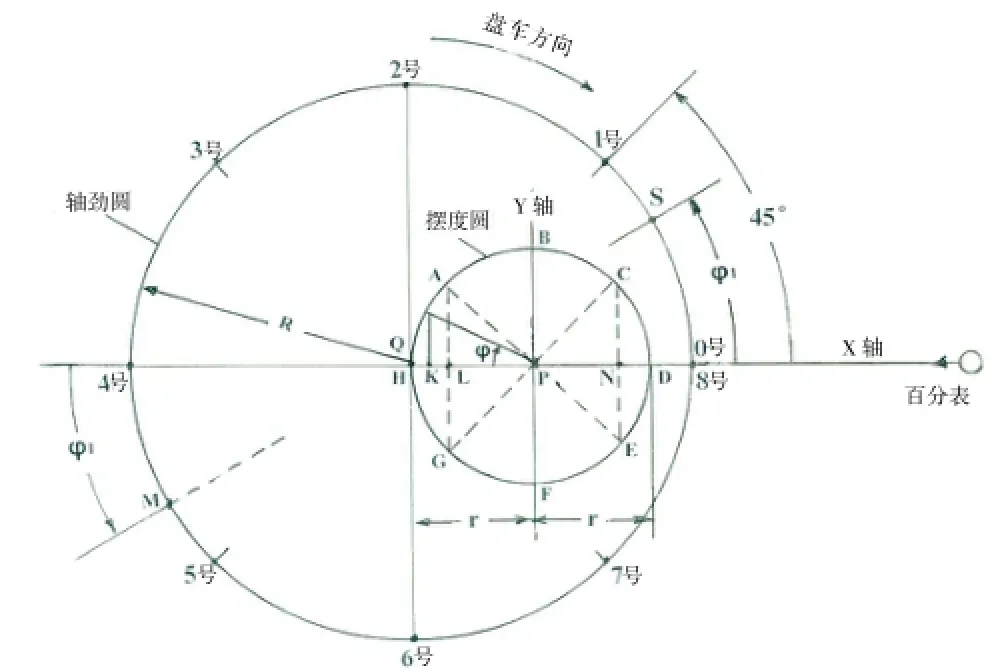
图2摆度圆P与轴颈圆Q的关系示意图（图上所示为Q点落在P圆H点上的情况）

首先，我们在摆度圆P的X轴上架设一个百分表，使其测头接触轴颈圆上的0号点（或称8号点），见图2，并且假定此0号点是轴颈圆上的最小摆度点，再设此时百分表指示值为“0”。正是因为轴颈圆圆心Q沿着摆度圆P的圆周的移动是由于轴颈圆的自转所引起，所以此时的轴颈圆圆心Q必定落在摆度圆圆周上的H点；而当主轴按俯视顺时针方向转动45°，当轴颈圆上的1号点与百分表测头接触时，轴颈圆圆心Q必将落在摆度圆圆周上的A点；依此类推，当轴颈圆上的2号、3号、4号、5号、6号、7号点分别与百分表测头接触时，轴颈圆圆心Q必将对应地落在摆度圆圆周上的B、C、D、E、F、G点。由于轴颈圆上的4号点与0号点相隔180°，可见，此4号点就是轴颈圆上的最大摆度点，而百分表所检测到的4号点与0号点之间的差值就是最大摆度值Jmax（即摆度圆直径2r值）。

此外，从图2可以看出，当Q点落在B点或F点时(或者说，当百分表接触到2号点或6号点时)，百分表指示值是相同的，都是HP=r；

当Q点落在A点和G点时(或者说，当百分表接触到1号点或7号点时），百分表指示值都应该是HL=HP-LP=r-rcos45°≈0.293r；

同理，当Q点落在C点和E点时（或者说，当百分表接触到3号点和6号点时），百分表指示值也是相同的，都是HN=HP+PN=r+rcos45°≈1.707r。

上述情况表明，在轴颈圆上位于最大-最小摆度点连线两侧对称的两个盘车点，其净摆度值（即百分表指示值）应当是相等的。如果把上述摆度值与盘车转角的关系画在图3上（关于这条曲线，下面还有详细叙述），就可看出，位于最大摆度点4号点两侧并且与它等距离(不一定都要相隔45°)的两点，其摆度值应当是相等的；同样地，从最小摆度点（0号点）来看，也具有这一特性。我们把这一特性称为最大-最小摆度点两侧摆度值的对称性。

图3理论的盘车摆度特性曲线

利用上述最大-最小摆度点两侧摆度值的对称性，我们可进行“验证盘车”，用于检查盘车质量。所谓“验证盘车”，就是，初步认为已经找到了轴颈圆上最大-最小摆度点所在的位置，通过再次盘车，检查盘车数据是否正确。如果发现某侧盘车点的摆度值与对侧盘车点的摆度值对称性较差，一般可怀疑所求取的最大-最小摆度的方位不准确；如果发现实测的各点摆度值与按上面公式算出的各点摆度值相差太大，也可怀疑盘车质量是否有问题。20世纪80年代以前，有国内外的好几台水电机组，在安装或大修中，盘车时间竟花费了10多天，其直接原因，都是由于没有及时发现盘车的工艺问题，究其深层次原因，都是由于当时对盘车数据之间存在的关系没有认识，因而在一大堆盘车数据面前莫衷一是，无法判断是否“离谱太远”。

2　盘车原理与盘车摆度计算公式

基于以上摆度圆和轴颈圆的概念，我们得知：当轴颈圆上每一点与百分表接触时，都对应着其圆心Q在摆度圆P圆周上的一个位置；Q点在摆度圆圆周上的每一个位置，又对应着它们在X轴上的一个投影点，而百分表检测到的正是Q点在摆度圆平面X轴上投影点的变化规律，所以，根据各个盘车点与百分表接触时的百分表指示值就可求出轴颈圆上最大摆度点所在的位置（方位）及其摆度值。这就是所谓的“盘车找摆度原理”。

在上一节里，我们在研究摆度圆和轴颈圆的时候，在它们圆周上标出的等分点都是相隔45°的，那是为了便于说明问题的做法。实际上，在图2的摆度圆上，如果我们以X轴为基准，按顺时针方向任取一个角φ，那么，当φ角从0°变到360°（即轴颈圆按顺时针转过360°)，百分表测头的被压缩值的变化规律应该是：

这里，HK就是我们所称的摆度值J，这样，就可把上式写成：

这个公式就是理论的盘车摆度计算公式，式中：r为摆度圆半径值（其数值是最大摆度值Jmax的一半），φ为盘车转角（即轴颈圆相对于百分表按顺时针方向转过的角度）。这个描述盘车摆度值变化规律的公式与作者在论文[1，3]里导出的公式完全一样，但本文的推导过程显然比前文简单直观的多了。

有人认为，在定义公式(1)里的φ角时，是按顺时针方向量度的，而三角学里的角度定义，都是按反时针方向量度的，所以公式(1)里的φ角应当标为“-φ”。在此，考虑到三角学里有公式cosφ=cos （-φ），所以公式(1)仍然是正确的。

根据公式(1)画出的关系曲线J=f(φ)称为理论的盘车摆度特性曲线。如果把上式中的φ值分别代以 0°、45°、90°、135°、180°、225°、270°、315°、360°，可算出对应J值分别是0、0.293r、r、1.707r、2r、1.707r、r、0.293r、0。这些数值正是我们在上一节研究中得出的结果。图3是理论的盘车摆度特性曲线图，其横坐标是盘车转角φ，φ角的起始点（即0号点）为最小摆度点，这时摆度值J= Jmin=0，在轴颈圆上与它相隔180°的那一点为最大摆度点，其摆度值J=Jmax=2r。该图纵坐标是以r表示的摆度值；在机组现场，r值通常都以0.01mm为计量单位。在图3上我们还同时标出了盘车转角0°、45°、90°、135°……等8个特殊角的摆度值。

3　最大摆度点所在方位及其摆度值的准确计算

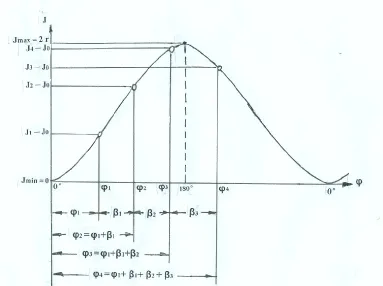
图4求解φ1和Jmin值时各参数关系图

下面，我们来研究一下如何求取最大摆度点所在方位角及其对应的最大摆度值问题。

首先，在轴颈圆上任取一个点作为研究问题的基准点，我们称它为“起始盘车点”，假设它距离轴颈圆上最小摆度点的方位角为逆时针方向φ1（即，其量度方向与各个盘车点的量度方向一致，换句话说就是，假设轴颈圆上的最小摆度点位于起始盘车点顺时针方向φ1角度的位置，见图2上的“S”点)。接着，画一条理论的盘车摆度特性曲线(图4)，其横坐标和纵坐标的标示与图3相同，同时设J1是与φ1相对应的百分表起始指示值。此后，进行所谓“任意转角盘车”，即，首先使机组主轴按俯视顺时针方向转过任意一个角β1，这时φ1角变为φ2角，与φ2角对应的百分表指示值变为J2；接着再使机组主轴转过任意一个角β2，这时φ2角变为φ3角，与φ3角对应的百分表指示值变为J3；……依此类推。我们把φ1、φ2、φ3……各角和J1、J2、J3……各点都标记在图4上。那么，根据公式(1)并对照图4，可列出如下关系式：

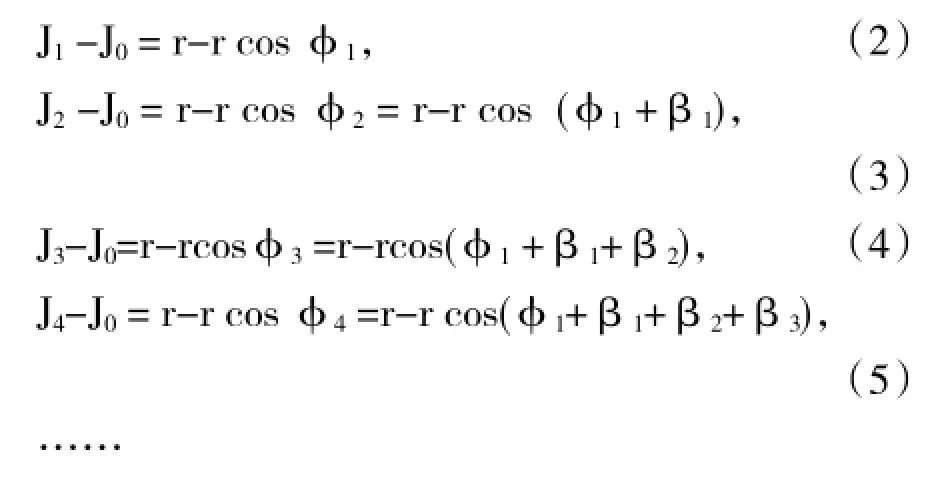
以上各式中的J0，是轴颈圆上最小摆度点通过百分表测头时百分表的指示值，称为百分表的“基础指示值”。因为以上各式都是根据理论的盘车摆度特性公式列出的，而应用公式(1)的时候有一个前提条件，即：0°的φ角位置必须是最小摆度点所处的位置，与其对应的百分表指示值J必须是0；现在进行任意转角盘车，不知道最小摆度点在哪里，与“起始盘车点”相对应的百分表指示值J1是随意选定的，这个J1值与把φ1值代入公式(1)算出的摆度值不一样，它们之间存在的差值正是J0，所以，在应用公式(1)列出上述各方程式时，都要减去百分表的基础指示值J0值。

在以上各式中，φ1、r和J0是未知数，而J1、J2、J3…和β1、β2、β3……都是已知数。在进行“任意转角盘车”时，随着转角β数量的不断增多，根据公式(1)写出的对应关系式也会跟着不断增多，而根据代数学的解方程原理，欲求出上述3个未知数，只需选取3个独立关系式就够。这样看来，我们只需在上面各式里任选3个方程式就足以求出φ1、r和J0。关于“任意转角盘车的摆度计算问题”，作者以前已经在相关论文[2]里作过探讨，在此不再赘述。

应当指出，用“任意转角盘车”的方法计算盘车摆度虽然在理论上是可行的，但由于其计算过程繁琐复杂，因而影响了它的应用。近年来有人根据盘车摆度计算公式编写了计算机程序，解决了这个问题。但作者认为，无需编计算机程序，只需测取4个特定盘车点的摆度值，通过简单的算术计算，查一下三角函数表，就可以方便地解决问题。具体做法就是，只要我们把式(3)、式(4)、式(5)中的β1、β2、β3都改成90°（也就是说，在盘车时使每次转角控制为90°），就可使计算工作大大简化。这样一来，上面各式就可写为：

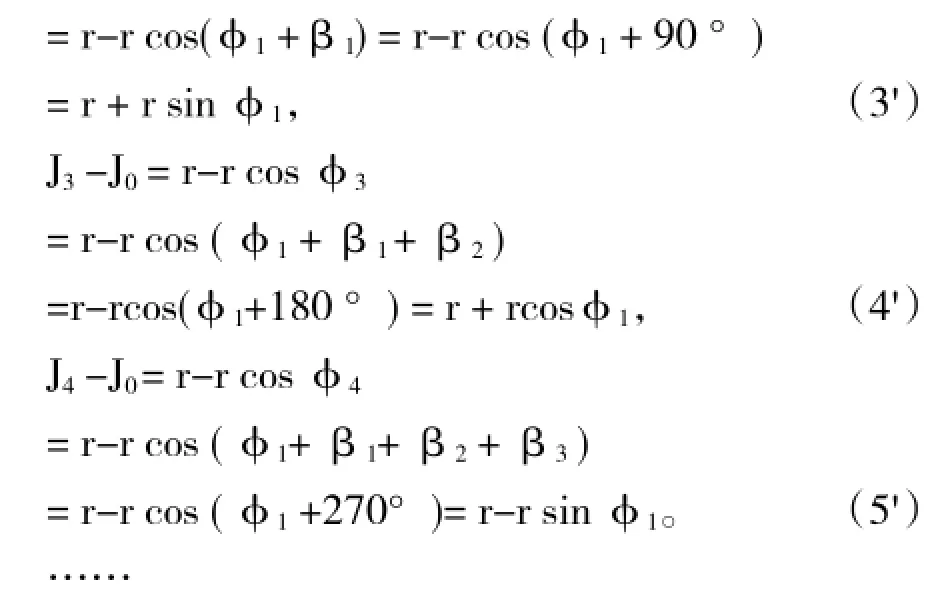
下面，我们改用B0表示以上各式中的J0，用Bs表示按90°盘车时起始盘车点(第1点)通过百分表时的指示值，用B90、B180、B270分别表示90°、180°、270°盘车转角时百分表对应的指示值，这样就有：

在上面4个方程式中，任取3个方程式都可以算出φ1、r和B0。在Bs、B90、B180、B270四个测定值中，对于式①里的Bs，考虑到在盘车过程中影响其测量准确度的因素可能多一些，所以下面我们不妨选取式②、式③、式④来求解：

式②-式④，得：

B90-B270=2rsinφ1，或者写成：

式③-式②，并利用三角函数的“诱导公式”和“和差化积公式”，得

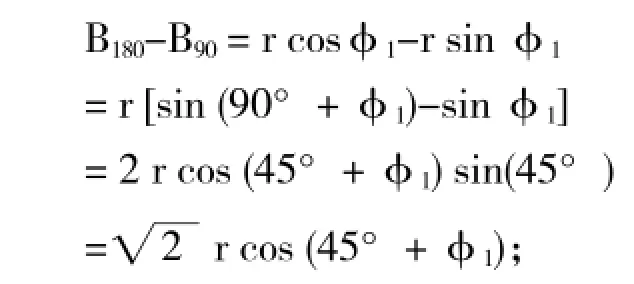
即

式③-式④，同样利用三角公式，得：

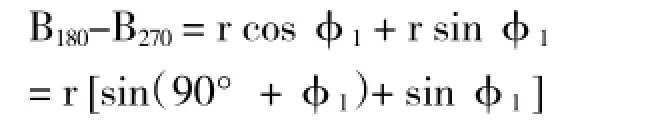
式⑦除以式⑥，有：

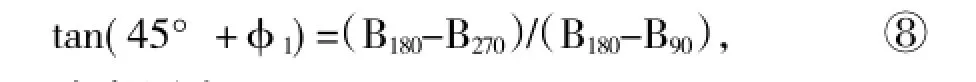
或者写成：

这样，根据式⑨就可求出φ1，把此φ1值代入式⑤，就可求出r。再根据式②、③或④，还可求出B0（不过，求B0值不是我们的目的）。由于盘车转角从90°改变到180°，以及从180°改变到270°时，与其对应的百分表指示值的变化都容易获取，这就使得盘车摆度的计算工作变得既简单又准确了。求出φ1值后，就可在轴颈圆上找到与最小摆度点相隔180°的最大摆度点所在的方位；求出r值后，就可知Jmax=2r。在此，再提请注意一下φ1角的方向，如果φ1角为正值，说明最小摆度点位于起始盘车点顺时针方向的位置；相对而言，负值的φ1角则表明要从初始盘车点反时针方向去度量最小摆度点的位置，这是我们在上述各公式推导过程中所规定的。

通过以上的理论研究可知，只要使机组主轴依次转过三个90°角，就可求出导轴颈处的最大摆度点所在方位角及其摆度值。具体做法就是：盘车时，首先在机组主轴轴颈圆上选定一个起始盘车点，记录下起始盘车点的百分表起始指示值Bs(从理论角度看，计算中用不到这个值，可以不记录，但从了解百分表的测量误差看，记下此值有一定意义)，接着使机组主轴按顺时针方向依次准确地转过三个90°角，取得B90、B180和B270各值，应用式⑨和式⑤，就可进行计算。在机组现场，工作人员把这种盘车测摆度的方法称为“四点盘车法”，也有人把它称为“90°盘车计算法”。

使用公式⑧或⑨时，发现在0°～360°范围内，存在两个“45°+φ1”角都符合“arctan[(B180-B270)/ (B180-B90)]”要求的情况，那么应当如何处理这个问题呢？在此，首先要注意这两个角的差值是180°，我们可以分别算出与其两个对应的r值，但会立即发现这两个r值是大小相等、符号相反的，显然，负值的r不在定义域内，当然不取；同时，对于被算出r是负值的那个φ1角，我们也不取。因此可知，在两组φ1、r值中，只存在一组是可用的。

在推广应用“四点盘车法”初期，对于有些以机械或电动盘车的机组，要使其依次“准确地转过三个90°角”，经常做不到，即在盘车停止位置上盘车点并没有按要求对准百分表，因而难以获得准确的测量数据。后来采取“在动态中观察百分表指示值”的方法，即，留意记录盘车过程中盘车点通过百分表测头时刻的指示值，方便地解决了这个问题。也有一些电站采取“倍增盘车点”的方法，即，把轴颈圆上等分的盘车点数增加为8点、12点、16点等，选取其中互成90°特性较好的点进行计算。还有一些电站，在熟练掌握盘车时机组转动部分的惯性运动规律后，认为可以做到使盘车点与百分表的错位值控制在±1.5cm以内。盘车时，通常都在轴颈圆处设置两组百分表，互成90°，这当然也有助于进行准确的数据测量。

为便于记牢公式⑨和公式⑤里的关键参数和算法，有人把这两个式子总结为两句话：一句是“180 减270，除以180减90，最后减45”，另一句是“90减270，再除以两倍正弦”。也有人利用现成的统计软件，输入不同组合的三个原始数据：B90、B180和B270，都可很快求出计算结果。

最后还要说明一下，在上述公式推导过程中，总是把最小摆度点所在方位角设为需要求取的未知数，而没有直接把最大摆度点所在的方位角设为未知数。这是因为，根据研究，如果直接求最大摆度点，公式的推导过程和对所得结果的表述将较复杂。况且，从最小摆度点去找最大摆度点如同把r值换算为Jmax值一样，都是很简单的事情。

4　应用“四点盘车法”计算盘车摆度的实例

以上对盘车原理及其摆度的计算方法作了论述，下面举两个实例来说明一下如何应用上述理论解决实际问题，并对几个需要注意的问题再作一次具体的介绍。

[实例1]有一台悬式水轮发电机组，测得其水轮机导轴颈处8个等分点的净摆度值如图5所示，求该轴颈圆上的最大摆度点所在的方位及其最大摆度值。

[解法说明]此例是每次递增45°的等转角盘车，在下面，我们利用式⑨和式⑤，分别取每个盘车点作为起始盘车点的情况都进行一番计算，这样，总共就要做8次计算。为了便于比较，做到一目了然，我们不妨把对这8个点的计算过程和结果归纳在一个表格里。详见表1。

在以上计算中，我们要注意以下几点：

（1）对于本例，如果不做准确计算，仅从8个盘车点里选最大摆度点，那么，直观地从净摆度记录圆图(图1)就可看出4号点是最大摆度点，并且Jmax =172-32=140。在此应当指出，由于初始盘车点是随意设定的，可见，用此法来决定最大盘车点及其摆度值显然是不准确的。

（2）在上述8个算例中，我们发现，根据式⑨都有两个“45°+φ1”角符合“arctan[(B180-B270)/ (B180-B90)]”的要求，而把求得的两个φ1角分别代入式⑤，算出两个对应的r值，它们大小相等、符号相反。显然，负值的r不在定义域内，当然不取。同时，对于被算出r是负值的那个φ1角，我们也不取。

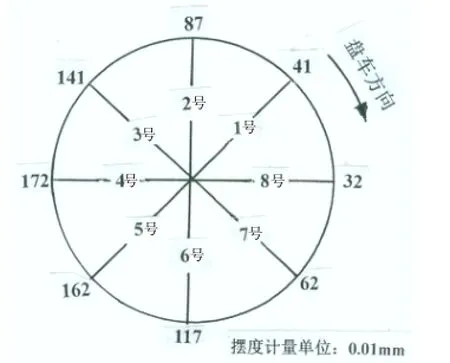
图5实例1的水导轴颈处净摆度值

图6　实例1的最大-最小摆度点所在的方位角（图上只示出取1号、2号、8号点为起始盘车点时的方位角）

表1实例1的盘车摆度计算汇总表

（3）表1里8种计算所求得的角φ1，都是最小摆度点所在的方位角，最大摆度点所在的方位角应当是φ1+180°或者φ1-180°。同时，8种计算都只算出r值，最大摆度值Jmax应当是2r。

（4）根据“最小摆度点位于轴颈圆上起始盘车点顺时针方向φ1角度的位置”的规定原则，此例的最小摆度点应当位于轴颈圆上1号盘车点顺时针方向33°的方位处；也可以说，最小摆度点位于轴颈圆上8号盘车点逆时针方向12°的方位处 (见图6上的“S”点)。当然，最大摆度点M应当位于轴颈圆上5号盘车点顺时针方向33°的方位处，或者说M点应当位于4号盘车点逆时针方向12°的方位处。(见图6上的“M”点)。

（5）从表1计算结果看出，随着所选取的起始盘车点以45°角的级差从1号到8号的依次变化，所算出的最小摆度点方位角数值也依次以45°的级差而变化。也就是说，与1号、2号……8号各盘车点相对应的φ1角分别是33°、78°、123°、168°、213°、258°、303°、-12°，它们的数值也都以45°的级差而递增。但各种计算所确定的在轴颈圆上的最大-最小摆度点方位却十分一致 (见图6上的M-S线)。8次计算所求得的“方位”如此一致，足以说明此次盘车质量是很不错的。相反地，如果所求得的最小摆度点所在方位比较杂乱，那就说明盘车质量有问题了。

（6）根据表1计算结果，r值分别有72.1、72.2、72.5、72.6诸数，这些数值都很相近，这也足以说明此次盘车质量是相当好的。在算出的各个r值中，以72.5居多（有3个），故取r=72.5，即Jmax=145比较合适。当然，如果所求得的各个r值相差较大，那就说明盘车质量不良。

（7）如果把r=72.5和1号点的φ1值(即33°）代入式（1），可得

J1=72.5×(1-cos33°)=72.5×0.161=11.6

这是1号点在理论的盘车摆度特性曲线上的摆度值，而在图5上标示的1号点的实测摆度值B1= 41，可知此处存在B0=B1-J1=41-11.6=29.4，由此可见，在此次盘车中，当轴颈圆上的最小摆度点通过百分表测头时，百分表的基础指示值B0应该是29.4；如果取2号点进行同样的计算，则有B0=B2-J2=87-57.4=29.6……当然，对B0的计算并非摆度计算所要求，之所以作这一“无用计算”，为的只是有助于我们对于前述B0、B1和J1各值之间关系的理解。

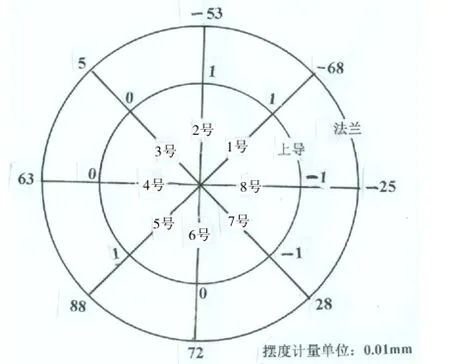
图7实例2的盘车摆度原始记录圆图

图8实例2的净摆度值圆图及其计算结果

（8）最后，最好再进行一次“验证盘车”。

以上是“解法说明”，叙述内容较多，为的是加深对本文理论部分的理解。实际上，在记住公式⑨和公式⑤以后，把有关几个数据代入，就可算出结果。如果使用现成的统计软件，即使进行表1的全部计算，也不费时。

[实例2]某水轮发电机单独盘车时测得上导轴承处和法兰盘处原始摆度值如图7所示，试确定最大摆度点的方位及其摆度值（注：本例的原始数据取自参考文献4）。

解：

（1）根据原始记录作净摆度值圆图，见图8。

（2）从图8可以看出，在本例的8个盘车点中，摆度最小的点是1号点(B1=-69)，摆度最大的点是5号点(B5=87)，由此可以初步认定：本例准确的最小摆度点应当在1号点附近，其最大摆度点应当在5号点附近。所谓进行“摆度计算”，就是把真实的最小摆度点究竟距离1号盘车点多少度算出来，再把最大摆度值算出来。在此，我们取1号点作为起始盘车点(Bs=B1=-69)，这时，“四点盘车法”的已知数据就是：B90=B3=5，B180=B5=87，B270=B7=29。

（3）根据公式⑨计算[B180-B270]÷[B180-B90]=[87-29) ]÷[87-5]≈0.7073，查“三角函数值表”得arctan （0.7073）≈35°或者215°，即φ1=35°-45°= -10°或者φ1=170°。我们在轴颈圆上把这两个角所对应的点都标出来(见图8)，显然，靠近较大净摆度值的那一点就是所求的最大摆度点(M)，而靠近较小净摆度值的那一点就是所求的最小摆度点(S)。同时发现，如果把φ1=-10°和φ1=170°分别代入公式⑤，即可算得r=(B90-B270)/2sinφ1=(5-29)/2sin（-10°）=69，或者r=（B90-B270）/2sinφ1=（5-29）/2 sin9（170°）=-69，可见，在这两个角中，无论取哪个角进行计算，只要取r的绝对值（即69），就可以算出最大摆度值Jmax=2r=2×69=138。

（4）在本例里，如果不取1号点作为起始盘车点，而分别取其它点作为起始盘车点进行计算，算出来的φ1角将稍有差别，显然，这是因测量误差引起的问题。根据现场经验，一般认为，如果各次计算结果的差值在5°以内，可选取适中的角度作为计算结果，如果此差值超过10°，建议再进行盘车测量为宜。