基于极值BMM模型的石油价格极端风险度量研究
2015-07-27刘飞郑晓亚
刘飞+郑晓亚


[摘要] 利用WTI日对数收益率数据估计一般极值分布参数,并根据极值BMM模型计算石油价格极端值风险。实证结果表明,在95%的置信水平下,由BMM模型度量的石油价格风险低于正态模型的相应度量值,而在99%的置信水平下,BMM模型对风险的捕捉则显著优于正态分布。上述结论表明,BMM模型在较低置信水平其效力虽不及正态分布VaR模型,但在高置信水平下能更好地捕捉分布的厚尾特征。因此,对于石油风险管理者而言,BMM模型将是测度石油市场极端风险较好的选择。
[关键词] 极值理论;BMM模型;石油价格;风险度量
[中图分类号]F810
[文献标识码]A
[文章编号] 1673-5595(2015)04-0007-07
一、引言
近代以来,石油已经成为一国经济发展最重要的战略资源之一,素有“工业血液”之称。从1993年起中国开始成为石油净进口国,伴随经济的快速发展,近年来供需缺口不断增大,对外依存度不断提高。在此背景下,国际市场上剧烈的油价波动难免会对中国宏观经济运行以及企业单位的生产经营产生较大冲击。如在新加坡上市的中航油公司由于违规参与石油期货的投机交易,造成55亿美元的巨额亏损。究其原因,主要是因为中航油公司对价格判断失误,内部没有完善市场风险防范措施,未能及时止损。目前,为规避石油价格波动带来的市场风险,许多国家推出了诸如石油期货、期权①在内的多个石油金融产品来分散市场风险。自1998年中国原油价格与国际接轨以来,为应对短期石油价格波动带来的巨大风险,国内企业纷纷借助国内和国外石油金融产品来减少石油交易风险,而加强市场风险研究、强化管理是较好规避石油价格波动风险的重要途径之一。因此,如何有效度量石油市场价格波动的极端风险,减少石油风险对宏观经济运行、企业生产经营产生的不利影响,保证中国经济的稳定快速发展,是当前面临的一项重要课题。
在石油市场价格风险方面,因极端事件发生的风险概率虽然很低,但其引发的极端市场风险却损害巨大,对风险管理者而言,如何有效监测极端风险也就显得十分重要。本文利用WTI日对数收益率数据估计一般极值分布参数,并在此基础上根据极值BMM模型开展石油价格极端值风险的度量研究。
二、文献回顾
风险度量,即风险的定量化计算。最开始的风险度量方法(名义值方法、敏感性方法、波动性方法)由于包括大量计算且不能为金融机构高管及监管人员提供一个关于整体风险的完整图像,已越来越不能满足金融市场度量风险的要求。这时,人们希望有一个简单的指标能够完全反映其在某一特定市场价格变动和某一特定期间下持有一定头寸的金融资产组合所带来的可能损失额。在此背景下,VaR风险度量方法应运而生。该方法将金融风险测度为一个确定的值,因其直观简捷,广为学界和业界所接受,已成为现在最流行的风险度量方法之一。
在石油价格风险度量方面,国外学者更倾向于对风险度量技术的分析,比如:Cortazar和Schwartz所构建的石油期货价格随机波动模型,它对样本内外数据均有很好的拟合能力,能够较好地及时规避价格波动带来的风险。[1]Cabedo和Moya在进行VaR测算时,通过标准历史模拟法、具有ARMA预测的历史模拟法以及方差协方差法的对比分析发现第二种方法能够有效地量化风险。[2]而Giot和Laurent在对Brent 和WTI现货日价格进行风险测算时,分别利用了Risk Metrics、Skewed TAPARCH 以及Skewed TARCH三种模型,他们认为Skewed TAPARCH法在两种商品价格风险度量中表现最好。[3]在国内,相关研究则更多地集中在价格风险测度以及相应的政策措施方面:冯春山等发现国际石油价格呈现较为明显的ARCH效应,认为石油企业应通过降低经营成本,建立以期货交易为主要手段的风险采购屏障等措施来规避价格风险。[4]潘慧峰和张金水的研究显示,极端情况国内原油价格的上涨风险平均水平要高于下跌风险的平均水平。[5]余炜彬等在研究原油市场规律的基础上,提出了一种对WTI现货价格进行预测的人工智能模型,这个模型能够运用历史数据检测原油价格风险。[6]在风险测度模型的选择上,张意翔等在对中国石油企业跨国并购的价格风险进行评价时认为,在976%的置信水平下,预测VaR值比实际值要大得多。[7]周莹和焦建玲基于GARCHVaR模型研究了石油价格风险,估计结果显示,GARCHVaR模型的估计结果比传统VaR结果更准确。[8]
然而,传统VaR方法对极端事件风险考虑不足,容易造成尾部风险的低估。极端事件发生的概率虽然很低,但其引发的极端市场风险却损害巨大,有时甚至是灾难性的,故对风险管理者来说,极端事件尤为值得关注。[9]为此,学者们将极值理论引入VaR度量中,利用其厚尾估计优势,修正传统VaR方法的不足,以便更准确地捕捉尾部极端风险。从上述国内外现有文献分析来看,现有研究中较少运用极值VaR方法去研究极端情况下的石油价格风险问题。因此,本文运用极值理论VaR模型度量石油价格波动的市场风险属较新的尝试。
中国石油大学学报(社会科学版)2015年8月
第31卷第4期刘飞,等:基于极值BMM模型的石油价格极端风险度量研究
三、石油价格极端风险度量实证分析
极值理论是度量极端条件下市场风险的一种方法,具有超越样本数据的估计能力,并可以准确地描述分布尾部的极端风险。它主要包括两种模型:区间极大值(Block Maxima Method, BMM)模型和越槛高峰 (Peak Over Threshold, POT)模型。本文运用BMM模型度量石油价格波动的极端风险VaR。为了便于开展实证分析,首先进行理论和方法介绍,根据有关文献简要说明分布形式、理论假设、BMM模型以及相应的VaR公式[910];其次,为确保实证结论有效性,对BMM模型的适用性进行检验;最后,得到参估及检验结果。
(一)极值定理及核心假设
假设金融资产收益率序列r1,r2,…,rn是独立同分布(iid)随机变量,n为样本容量,F(r)是未知总体分布,r*n 为区间极大值,若存在常数序列an>0、bn∈R和非退化的分布函数族F*(r),满足
Pr*n-bnan≤rdF*(r) (1)
则称F*(r)为一个极大值分布族,其中,d表示弱收敛于某分布;an是尺度序列,表示离散程度,相当于标准差;bn是位置序列,表示集中趋势,相当于平均数。极大值分布族F*(r)包含了三种类型的极限分布。为了避免模型预设错误,可以经过变换,将三种类型分布族归纳为以下一个单参数的分布族。
F*(r,ξ)=exp-(1+ξr)-1ξ, ξ≠0
exp(-exp(-r)), ξ=0 (2)
式中,当 ξ≠0 时,1+ξr>0, α=1ξ,满足式(2)的F*(r,ξ)称为广义极值分布(generalized extreme value distribution,简记为GEV分布)。当引入位置参数μ和尺度参数σ后,GEV分布F*(r,ξ)扩展为具有三个参数的分布
F*(r,μ,σ,ξ)=exp-1+ξr-μσ-1ξ, ξ≠0
exp-exp-r-μσ, ξ=0 (3)
式中,ξ为形状参数,称之为GEV分布的极值指数(extreme value index,EVI),ξ值越大则尾部越厚。
(二)模型介绍
BMM模型一般应用上述GEV分布处理样本极值,具体步骤如下。
第一步,样本区间的划分。
对于给定的样本若只有一个最大值,而由于GEV分布包含三个参数,仅有一个最大值无法进行参数估计,因此本文采用文献中经常运用的区间取值法(Block Method),即将总样本r1,r2,…,rn分割为若干互不重叠的子样本区间:[r1,…,r1+k],[r2+k,…,r2+2k],…,[rm+k,…,rn],然后针对每个区间取最大值,当k充分大时,我们希望极值理论对每个子样本都适应。在应用中,k的大小由实际情况来决定。例如,日收益率k=21近似对应于1个月的交易日数量,k=63近似对应于1个季度的交易日数量。
第二步,GEV分布参数的估计。
GEV分布参数的估计方法很多,例如极大似然法、回归方法等。本文采用极大估计方法计算位置参数μ、尺度参数σ、形状参数ξ。
令r1n,r2n,…,rmn 表示区间j=1,…,m的极大值。
则当ξ≠0时,扩展GEV分布的极大似然函数为:
Ln(ξ,μ,σ)=-mlog(σ)-
1+1ξ∑mi=1log1+ξrin-μσ-∑mi=11+ξrin-μσ-1ξ (4)
当ξ=0时,扩展GEV分布的极大似然函数为:
Ln(ξ,μ,σ)=-mlog(σ)-∑mi=1rin-μσ-
∑mi=1exp-rin-μσ (5)
由于对数似然函数方程(4)、(5)不存在解析解,可以运用非线性估计程序来得到位置参数μ、尺度参数σ、形状参数ξ的极大似然估计值。理论研究表明,上述估计参数在正则条件下,具有最小方差。
第三步,风险值的计算。
根据参数估计值,本文首先集中讨论持有空头的金融头寸所面临的风险,所以感兴趣的是右尾分位数。令p*为一个小概率,它表示一个空头头寸的潜在损失超过一定限度的可能性,且r*n 为子区间最大值在极限为一般极值分布条件下的p*分位数,则有
p*=1-exp-1+ξ(r*n-μ)σ, ξ≠0
1-exp-exp(r*n-μ)σ, ξ=0 (6)
利用式(6)可推导出r*n,
r*n=μ-μξ{1-[-ln(1+p*)]ξ}, ξ≠0
μ-σln[-ln(1+p*)], ξ=0 (7)
值得注意的是,式(7)只是子区间最大值在极限为一般极值分布条件下的p*分位数,尚不是观测的极值序列的p分位数VaR。假定资产收益率序列无关,利用子区间最大值与观测收益率序列之间的关系,可以得到观测极值序列右尾p分位数的VaR,在式(8)中用VaRU标识:
VaRU=μ-σξ{1-[-ln(1-p*)]ξ}, ξ≠0
μ-σln[-ln(1-p*)], ξ=0 (8)
极小值分布与极大值存在一一对应的关系,即
min{r1,r2,…,rn}=-min{-r1,-r2,…,-rn} (9)
利用式(3)、(9),可以进一步推导出观测极值序列左尾p分位数的VaR,标识为VaRL:
VaRL=-μ-σξ{1-[-ln(1-p*)]ξ}, ξ≠0
-μ-σln[-ln(1-p*)], ξ=0 (10)
(三)数据选取
石油市场的价格风险主要是由石油现货价格和期货(期权)价格的波动引起的。其中,原油现货价格波动是引致风险的主要原因。目前,国际上的原油交易主要以三大原油WTI、Brent和Dubai为基础,其中以WTI原油市场的影响最广泛。基于此,本文主要选取WTI原油现货市场价格进行世界石油现货市场价格风险的实证研究。本文选取2003年1月2日至2012年9月6日的2500个数据,数据来源于Energy Information Administration。考虑到简单收益率的非正态性特征,故选取对数收益率形式。令:
Rt=100×lnPtPt-1=100(lnPt-lnPt-1),t=1,2,… (11)
式中,Pt为t时刻的原油出售价的观察值,为便于计算,将Rt放大100倍。
(四)BMM模型适用性检验
BMM模型的运用依赖于WTI收益率数据是否满足其模型条件。为此,首先需要做正态性检验、序列相关性检验、平稳性检验。
1.正态性检验
利用已观测数据作为样本,计算得到WTI日收益率描述性统计,见表1。从表1可以看出,均值较小,标准差却较大,偏度为负,呈左偏;峰度值大于正态分布的峰度值3,表现尖峰形态;符合通常资产收益率分布的尖峰、厚尾、偏态特征,均值附近与尾部的概率比正态分布大,介于均值附近与尾部的中间过渡部分的概率比正态分布小。JB统计量显著拒绝正态性假设。
表1WTI收益率描述性统计
统计量统计值统计量统计值
均值005标准差168
中位数016偏度-037
最小值-843峰度655
最大值1280JB统计量1370
为了直观地呈现WTI价格走势以及收益率的变化情况,本文分别绘出了WTI价格走势图和日收益率序列变化图,见图1、2。从图1、2中可以看出,石油价格虽然在2008年金融危机时明显下降,但总体表现出逐步增加的趋势。日收益率除2008年波动较大外,其余年份均较为平稳。
图1WTI价格序列走势
图2WTI收益率序列的变化
2.序列相关性检验
对WTI日收益率进行LjungBox检验,结果见
表2。由表2可知,WTI收益率存在明显的序列相关性,因此,WTI收益率不满足极值类型定理要求的序列独立性要求。
表2WTI价格序列Ljung-Box检验
滞后期数自相关系数偏自相关系数Q统计量概率P值
102102811546000
2001-00811566000
300600712489000
400400612837000
3.平稳性检验
最常用的平稳性条件的检验是单位根检验,主要有ADF检验、PP检验、DFGLS检验等。由于是日收益率数据,本文采用不带漂移项和趋势项的ADF检验、PP检验,见表3。结果显示WTI日收益率序列的t统计量值均大于这两种检验显著水平为1%时的临界值,故拒绝存在单位根的原假设,即该序列是平稳的。
表3WTI收益序列的平稳性检验
ADF检验t统计量P值-3322000PP检验t统计量P值-3353000
临界值1%显著性水平-343
5%显著性水平-28610%显著性水平-257
临界值
1%显著性水平-3430
5%显著性水平-2860
10%显著性水平-2570
以上检验表明,WTI日收益率序列非正态、非独立但具有平稳性。极值类型定理要求数据相互独立,故不满足传统极值类型定理的条件。但随着研究的深入,人们认识到极值理论条件可以放松到弱序列相关的观测值。假定rt的自相关函数是平方可积的(即∑∞i=1ρ2i <∞,其中ρi是rt的滞后i的自相关函数),1964年Berman证明了极限极值分布的同样形式对平稳非正态分布也成立。BMM模型是按子样本区间取极值,只要子区间足够长时,满足平稳分布条件的序列,就符合自相关函数符合平方可积条件,故可以认为WTI日收益序列符合BMM模型条件要求。
(五)GEV分布参数估计与拟合检验
当子区间长度为21天时,WTI收益率可得到119个极值数据。极值数据平均间隔约30天,大约对应于1个月,可基本满足BMM模型条件要求。图3、4分别为WTI收益率子区间最大值与最小值对数收益率的变化图。
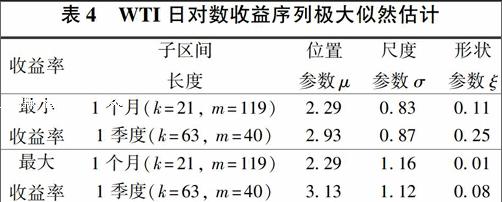
下面对WTI收益率应用最大似然法来估计一般极值分布的位置参数μ、尺度参数σ、形状参数ξ,表4概括了子区间长度为1个月和1个季度的估计结果。由表4可以得出以下观测结果:当k增加时,参数μ、σ变大是可以预料的,因为子区间最小值和最大值的期望值是k的非减函数;形状参数的估计结果不够稳定,主要原因是k=63时的子区间长度较小,致使结果具有一定的可变性。
图3WTI收益率区间最大值的变化
图4WTI收益率区间最小值的变化
一般来说,BMM模型会受子区间长度的影响,子区间较长时,极值数据较少,对厚尾的刻画精度较高,但拟合误差也随之增大,故需要对子区间长度进行拟合检验。为了直观呈现拟合效果,本文分别绘制WTI收益率分布左、右尾散点分布图以及残差QQ图,详见图5~8。在残差散点分布图中,拟合曲线穿过散点最密集的部分,QQ图大致围绕直线分布,表明以21天为单位取极值时,BMM模型拟合是合理的。
表4WTI日对数收益序列极大似然估计
收益率子区间
长度位置
参数μ尺度
参数σ形状
参数ξ
最小
收益率
1个月(k=21, m=119)229083011
1季度(k=63, m=40)293087025
最大
收益率
1个月(k=21, m=119)229116001
1季度(k=63, m=40)313112008
注:在应用中,k的大小由实际情况来决定,例如,对于日收益率k=21近似对应于1个月内的交易日数量,k=63近似对应于1个季度的交易日数量。m表示第m个子区间。
图5WTI收益率左尾残差散点分布
图6WTI收益率左尾残差QQ图
图7WTI日收益率右尾残差散点分布
图8WTI日收益率右尾残差QQ图
(六)VaR估计与检验
在上述参数估计的基础上,计算95%和99%置信水平下的VaR,并与正态分布VaR相比较,计算结果见表5。为便于区别,分别用VaRB、VaRN表示BMM模型和正态分布模型所度量的VaR。
根据VaR的定义可知,如果收益率rt服从标准正态分布,在置信水平1-α下,VaR的计算公式为:
VaRN(rt)=-Φ(α) (12)
式中,Φ(α)为标准正态分布函数的反函数。进一步,根据正态分布及VaR的性质,可得对于服从一般正态分布rt的VaR,则:
VaRN(rt)=μ+σVaRN(εt) (13)
表5WTI日收益率的VaR
置信水平
(%)VaRB左尾右尾
VaRN左尾右尾
95221223269282
99421369322335
表5中,95%置信水平下WTI收益率右尾所对应的值VaRB为223,它表示在正常市场情况下,WTI的对数收益率在100天中大约有5次高于223%的情况,表5中其他数据的解释与此相似。进一步分析表5中的VaR可以发现,在95%的置信水平下,BMM模型对WTI收益率风险估计值低于正态分布VaR模型估计值。而当置信水平为99%时,BMM模型对WTI收益率风险估计值要显著高于正态分布。这表明在95%的置信水平下正态分布VaR模型会高估WTI收益率的极端风险;在99%的置信水平下,则反之。
因表5中的VaR值分别由BMM模型和正态分布模型计算得到,故需要对其预测结果的准确性进行检验。为了检验这两种模型下VaR对实际损失的覆盖程度,本文采用Kupiec双尾检验法(two-tailed test)似然比统计量LR。这个统计量基于这样的一个事实:在容量为n样本中出现m次损失超过VaR的概率由一个二项分布给出。假定VaR中例外发生的概率为p,而在n个观察日中例外发生了m次,则LR统计量计算公式如下:
LR=-2ln[(1-p)n-mpm]+2ln[(1-m/n)n-m(m/n)m] (14)
当n充分大时,LR服从χ2(1)的渐进分布。当例外发生的次数很高或者很低时,由式(14)计算出的统计量会比较大。在χ2(1)分布中,变量的值大于384的概率为5%,因此,式(14)计算出的统计量大于384时,就可以拒绝模型假设。
根据表6的Kupiec检验结果,在95%的置信水平下,BMM模型左尾LR统计量是2743,概率P值为000;右尾LR统计量是1606,概率P值为000,表明BMM模型是失效的。正态分布左尾LR统计量是001,概率P值为092,右尾LR统计量是1433,概率P值为001,表明正态分布能够很好度量左尾风险,而右尾则是失效的。而在99%的置信水平下,BMM模型左尾LR统计量是235,概率P值为013,右尾LR统计量是182,概率P值为018,表明无论是左尾还是右尾,BMM模型都是非常有效的。而正态分布左尾LR统计量是8951,概率P值为000,右尾LR统计量是1554,概率P值为000,表明正态分布无论是左尾还是右尾都是失效的。综上分析,本文认为BMM模型在高置信水平下能更好地捕捉到分布的厚尾特征,在较低置信水平下则效力尚不及正态分布VaR模型,这和目前有关极值理论研究的一般结论吻合,与田新时、花拥军等的观点相同。[1011]
表6WTI日收益率VaR的Kupiec检验
模型
VaR
BMM模型VaR(5%)VaR(1%)
正态模型VaR(5%)VaR(1%)
尾部左尾右尾左尾右尾左尾右尾左尾右尾
LR统计量LR的P值
27431606000000235182013018001143309200189511554000000
四、结论及建议
本文利用WTI收益率数据估计一般极值分布参数,并根据BMM模型中VaR公式计算石油价格风险,结果表明,在95%的置信水平下,正态分布对风险的捕捉要略优于BMM模型;但在99%的置信水平下,BMM模型对风险的捕捉则显著优于正态分布。上述结论说明,BMM模型在高置信水平下能更好地捕捉到分布的厚尾特征,在较低置信水平下则效力不及正态分布VaR模型。因此,对于石油风险管理者而言,BMM模型将是测度石油价格极端风险较好的选择。
准确度量WTI原油现货市场价格波动的极端风险有较好的现实意义。宏观上,对国家控制石油进口风险具有一定的借鉴;微观上,能够使石油进口企业更好地规避市场极端风险。本文的研究目的只是为极值理论VaR方法在石油风险度量中的应用起一个抛砖引玉的作用,期望石油风险管理者能够运用该方法更好地度量极端风险。
石油风险控制是一项较为复杂的系统工作,为了进一步提高石油风险管理水平,本文建议在有效测度石油收益率VaR的基础上要做好以下几方面工作:第一,利用BMM模型测度WTI日收益率的VaR,根据模型估计结果,制定可浮动的WTI收益率VaR区间,检查石油交易头寸的风险程度并采取必要的交易措施进行市场操作,将石油风险控制在设定范围内。第二,石油风险度量的基础在于理论模型,而理论模型与现实之间存在一定的差距,需要定期地进行参数调整与模型优化。要根据石油市场交易信息,结合宏观经济状况和国内外整体形势对模型设定进行优化,以提升模型预测能力。第三,建立石油供应保险制度,使石油供应中断的风险由国内外相关用油各方共同承担。这一思路的提出,是基于现代金融的第二个基本原理,即对不能分散的风险,应由各方共同分担。第四,改善能源供应环境,多方拓展供应路线(如计划从俄罗斯、塔吉克斯坦、非洲等地区进口),努力改变目前从中东进口石油为主的格局,实现石油供应区域的分散化。
注释:
① 中国曾在1993年推出过石油期货交易,在开市一年多的时间里,总成交额达到1 000亿元人民币,当时列世界第三位,仅次于NYMEX和IPE。后来由于种种原因,中国取消了原油、成品油价格的“双轨制”,改为国家统一定价。在此情形下国内石油期货交易被迫停止。目前,国内仅有一款燃料油期货品种,由上海期货交易所2004年8月25日推出,石油期货国内尚未推出。
[参考文献]
[1] Cortazar G, Schwartz S. Implementing a Stochastic Model for Oil Futures Price [J].Energy Economics, 2003, 25(3): 215238.
[2] Cabedo J,Moya I. Estimating Oil Price Value at Risk Using the Historical Simulation Approach [J].Energy Economics, 2003, 25(3): 239253.
[3] Giot P,Laurent S. Market Risk in Commodity Markets: a VaR Approach [J].Energy Economics, 2003,25(5):435457.
[4] 冯春山,吴家春,蒋馥.国际石油市场的ARCH效应分析[J].中国石油大学学报:社会科学版,2004,19(2):1820.
[5] 潘慧峰,张金水.用VaR度量石油市场的极端风险[J].运筹与管理,2006,15(5):9498.
[6] 余炜彬,范英,魏一鸣.基于极值理论的原油市场价格风险VaR的研究[J].系统工程理论与实践,2007,8(8):1220
[7] 张意翔,胥朝阳,成金华.基于VaR方法对中国石油企业跨国并购的价格风险评价[J].管理学报,2010,7(3):440444
[8] 周莹,焦建玲.基于GARCHVaR模型的石油价格风险研究[J].合肥工业大学学报:自然科学版,2011,34(9):14231427
[9] 花拥军.极值理论及其在沪深股市风险度量中的应用研究[M].北京:科学出版社,2011.
[10] 田新时,毛洪云.基于POT模型的风险价值估计[J]. 华中科技大学学报:社会科学版,2003,6(5):97100
[11] 花拥军,张宗益. 极值BMM与POT模型对沪深股市极端风险的比较研究[J]. 管理工程学报,2009,23(4):104108
[责任编辑:张岩林]
Risk Measurement of Oil Price by Implementing BMM Model
LIU Fei1, ZHENG Xiaoya2
(1.Guangzhou Rural Commercial Bank, Guangzhou, Guangdong 510623, China;
2.Postdoctoral Research Station, Shanghai University of Finance and Economics, Shanghai 200433, China)
Abstract: The paper estimates parameters on the general extreme value distribution using WTI return and we calculate the risk of oil price using VaR formula deduced from the BMM model. The results show that the risk measured by BMM model is lower than by the normal model in the 95% confidence level, and vice versa, in the 99% confidence level. It illustrates that the higher confidence level is the more BMM model which can capture the heavy tail characteristics of the distribution. However, the effectiveness is less than normal distribution in the lower confidence level. Therefore, BMM model will be a better choice to measure the extreme risk for manager in oil market.
Key words: extreme value theory; BMM model; oil price; risk measurement
[收稿日期] 2014-12-31
[基金项目] 山东省软科学研究计划一般项目(2014RKE28045);中央高校基本科研业务费专项资金资助项目(14CX06042B)
