刍议从联系的角度培养学生的问题意识

陈为强

一、缘起

为了调查学生从联系的角度提出问题的状况，我们采用了问卷调查的方式对下面两道题目进行了调查。

本次调查采用无记名方式，不需要和别人讨论，谢谢您的配合！

1.树叶情况。

从上面图形中您想到了什么？

2.

从上面图形中您想到了什么？

二、分析

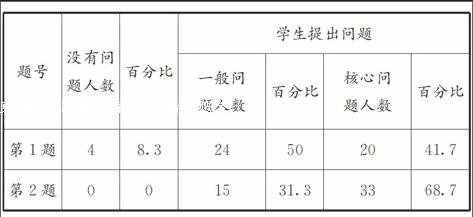
学生在没有任何心理负担的情况下完成问卷，收回有效问卷48份。随后，笔者对问卷的结果进行整理汇总。

从上面的数据反映出学生面对鲜活的“综合与实践”教学素材时，虽然小部分学生具有一定的问题意识，但还是流于形式，只能提一些没有多少思维含量的一般性问题。譬如，题1学生提出“一共有多少片树叶”“叶子比较宽的树叶比细长的树叶多几片”等浅问题;题2学生提出“每个图形各有几个黑点”“下一个图形中有几个黑点”等碎片问题。但也令人欣喜地看到，有相当多的学生提出“为什么同一种树叶大小不同，却很相似”“柳树叶和竹叶属于不同树的叶子，看起来为什么很相似”“第100个图形中有多少个黑点”“m边形中有多少个黑点”等具探索性、思辨性的优质核心问题。好问题对于学生的学习有着极大的驱动力，它拨动学生思考之弦，促使学生去做深度思考，帮助学生得到应有的知识。

但也应发现：为什么题2提出优质问题的人数要比题1提出有价值问题的人数多，且差距较大。笔者分析题2的结构性强、规律性特征明显，便于学生运用前后联系的视角去观察、分析与归纳，易于提出统整性的数学问题：“m边形中有多少个黑点？”反观结构性不够明显的题1，有一半的学生缺乏对于事物基于感觉到的处于相似之处的碎片化的信息整合起来的能力，无法洞察其内在的相似之处，无法提出高层次的、具有概括性的核心问题，自然就不能把复合思维抽象为前概念思维。

三、对策

1.置学生于有结构的实物中，发展用联系的观点提出问题的意识。

“综合与实践”活动的开展，要努力体现“注重综合、强调实践”的特征，注重在情境中、操作中生发学生的问题意识。依据学生的年龄特点，要放手让学生动手操作，因为必要的动手操作是学生感知的基础，是发现问题、探究问题的根源。所以教师将学生置于有结构的材料中（例如大小不同的树叶），由学生亲自摆弄、触摸、把玩，引导学生去观察、思考，充分利用学生探究中产生的好奇、好问、困惑、矛盾的心理特点，产生“不同树的树叶形状为什么不同？”“同一种树叶虽然大小不同，但为什么都很相似？”“有些树叶虽然不属于同一种，但为什么也相似？”等逐步深入的思辨性问题。这些问题表征透视学生的视角不再只关注某一类型树叶，而是聚焦不同类型的树叶，通过前后联系、左右对比发现它们异同之处，借机发展学生的求同思维和求异思维。

我们还应该看到教师给予学生的感性材料越完善、越丰富，学生运用联系的观点观察事物、生发问题的意识也就越强，洞察事物本质的能力越容易形成。“心理学”表明：越是丰富的视觉表象、心智图像对于学生学习力的培养越有利，形成的结构性、抽象性的能力越稳定。因此，教师在教学中要多为学生提供丰富的结构性事物，鼓励学生主动思考、大胆猜想，“再创造”出对自己来说属于新鲜的数学问题。也可以启发学生将文本知识与数学实验、生活实践联系起来，提炼出数学问题和数学模型，发现“生活中的数学”，切实体会到“处处留心皆学问”的道理，积累用联系的眼光去观察生活的经验，学会数学式地提问和数学式地表达。

2.引导学生从熟悉的事物中，生发类比发现问题的能力。

对于同一类事物，引导学生通过观察、归纳、分析、概括，异中寻同，发现它们的内在联系，通过类比提出问题。例如，学生学习完“分数和除法的关系”后，凭借其已有的知识基础，引导学生产生“除法中有商不变的规律，分数中是否也存在类似的规律”的类比性问题，运用知识迁移的能力，让学生经历“猜想→尝试→验证”的科学发现历程。这样的教学容易使学生所学的知识形成系统性、结构化，使已有的知识具有衔接性和生长力。教师在教学时还可以打破数与形的障碍，实现数与形的完美结合。

例如，教师在课始出示生活中和自然现象中许多美丽的对称图像，引发学生做出类比思考：“四则运算中是否也隐藏着类似的对称现象呢？”一个具有拓展性的问题，为学生打开了一个广阔的思维空间。学生的探究热情得到点燃，纷纷拿出自己的练习本尝试举例，寻找具备类似规律的题目。经过交流，一些学生零星地找到了诸如“46+75=57+64”“85+69=96+58”“64×23=32×46”“14×82=28×41”等具有对称性的题目。其他学生经过估算、笔算，发现算式具有对称性，学生对这种现象充满了好奇，并乐此不疲地进行举例、计算，试图破解其中隐藏的规律。学生不断地尝试、修正，最后从数的组成角度理解其中的道理。例如，对称中的加法“46+75=57+64”，等号左右两边的个位和十位的计数单位的个数同样多;乘法则是等号左右两边个位数的乘积和十位数的乘积分别相等，就如“64×23=32×46”。学生发现了其中的结构美，从而心智得到充实，能力得以增长。在教学中教师善于引导学生通过类比提出问题，然后把有价值的问题加工成话题，甚至是“小课题”，这样就会使得学生思维“活泛”起来，课堂“兴奋”起来。

3.充分利用结构性较强的题目，催发学生形成统摄性问题的观念。

数学的抽象性还表现为它的高度概括性，它使用大量的数学符号进行表征与推演。数学表达的形式化也加深了数学抽象的层次，折射出学生分析能力和概括能力的提升，这也是学生求简意识发展的必然趋势。对于结构性较强的题目，例如调查问卷中题2，教师可以引导学生从关注具体的量（第几个图形有几个圆点）提升为聚焦图与图之间的联系（能否用一个字母式表示边数和圆点个数之间的关系），这样问题就有了统整性，用一个解析式来对一类题目进行表征，既达到求简的目标，也渗透了代数意识和代数思想，发展学生的抽象思维。

当然，学生的思维水平决定了他们在很大程度上离不开具体事物的直观支撑，离不开图形的积累和导引。教师长期引导学生运用字母符号表征问题，学生就能从一些看似具体的、复杂的、表面不相干的和不同类型的事物中抽象概括出它们共同的关系式，找出它们共有的属性，把一些图形的性质赋予数量的意义，得出恰当的数量关系式，将几何问题代数化，达到以数助形的目的。这种做法深度契合学生的思维从实物表象概念过渡到内部心理表象概念的要求，即相关的概念可以脱离实物，表征事物之间的关系。同样，我们还可以反过来提出一个具有包容性问题，让学生思维从封闭走向开放，从单一走向多元。例如，在学生完成“圆柱的表面积灵活运用”时，让学生思考：“2πrh这样的式子，能解决哪些生活问题”这样“以一抵多”的问题，引导学生发散思维，用数学的眼光来审视生活。学生提出了这一式子能解决“做一个烟囱需要多少铁皮？”“一个压路机滚动一周能压路多少？”“圆柱形四周贴一圈包装纸的面积为多少？”等鲜活的生活问题。学生深刻感受到一个表达式的简洁和其相对应的生活内容的丰富，完成对于不同生活情境的知识归类，使得学生的知识系统结构化。

（作者单位：江苏省徐州市贾汪区实验小学）endprint