振动机械滚动轴承单点点蚀故障动力学研究

杨洋，段志善，郭宝良，李恒

(西安建筑科技大学 机电工程学院，西安 710055)

滚动轴承是旋转机械的重要组成部分，轴承故障中90%由内外圈故障引起[1]，点蚀故障是其主要形式。提取轴承的故障特征频率是诊断轴承故障的关键[2-4]，目前轴承故障建模方法已经比较成熟：(1)通过脉冲序列模拟滚动体通过缺陷时产生的冲击振动[5-8]；(2)滚动体通过缺陷时会释放一定的变形，引起接触载荷发生突变，导致轴承产生冲击振动[9-12]。

目前，国内对于故障轴承的动力学研究相对较少，振动机械领域则更缺乏[13-15]。文献[8]比较早地将EHL(弹性流体动力润滑)、波纹度及缺陷联系在一起进行讨论。文献[16]将点蚀故障轴承模拟为两自由度系统，利用载荷与位移之间的关系建立了比较完整的轴承动力学模型。文献[10-11]将两自由度模型进行了改进，使模型更加切近实际情况。但上述故障模型均以旋转机械为基础建立，其结论并不能直接应用于振动机械。

文献[12]建立了振动机械轴承内圈和外圈单点故障的脉冲冲击模型，提出了该类型故障判别依据。通过对振动机械轴承工作状况的分析，以第2种建模方法建立了振动机械轴承内、外圈单点点蚀动力学模型，以振动筛为研究对象验证了理论模型，并与旋转机械轴承内、外圈单点点蚀故障进行了比较。

1 振动机械轴承动力学模型

以圆振筛为研究对象，振动机械轴承的工作简图如图1所示，由于系统中存在k>>ks和c>>cs,可以将其分解为2个部分：(1)轴承随系统在激振力的作用下一起运动；(2)轴承自身旋转时，由于滚动体受力而发生形变，从而引起内外圈的相对运动。

图1 振动机械轴承振动模型

对于轴承随系统在激振力作用下的振动，以水平方向为x轴，竖直方向为y轴，系统运动可描述为

(1)

式中：M为系统质量；m为轴系等效质量；cs为系统阻尼；ks为系统刚度；k为轴承等效刚度；c为等效阻尼。

以轴承为个体，其受力情况如图2所示。图中Fr为轴系受到的激振力，G为自身重力，ωs为轴系旋转角速度。

图2 轴承工作状态示意图

由于载荷的作用，钢球与内、外圈沟道之间会发生接触变形，接触副可用弹簧阻尼模型表示，钢球质量远小于套圈质量，因此钢球两端的弹簧阻尼近似为串联形式[8]。

假设在转动时，内、外圈沟道与钢球之间无滑动，若外圈在水平与竖直方向相对内圈移动距离分别为x和y，根据牛顿第二运动定律，其两自由度振动方程为

(2)

式中：mz为轴承参振部分质量；cx，cy分别为x，y向轴承等效阻尼；Fx，Fy分别为x，y向所受外力；Fbx，Fby分别为x，y方向所有钢球接触载荷之和。

1.1 外圈单点点蚀

轴承外圈受力如图3所示，将轴承的振动看作外圈相对内圈的运动。以水平向右为x轴正向，竖直向上为y轴正向。

图3 外圈有单一点蚀时轴承模型

当轴承振动使外圈相对于内圈在水平和竖直方向分别移动x和y时，由于故障缺陷的存在，当第j个钢球通过缺陷时，会释放一定的变形量，而钢球与缺陷相对位置会引起不同的变形量λ，因此引入开关量βj，则钢球与内、外圈接触总变形量δj为

δj=xcosθj+ysinθj-Gr-βjλ,

(3)

(4)

(5)

(6)

式中：Gr为径向游隙；ωc为钢球公转频率；Z为滚动体个数；Dw为钢球直径；Dpw为球组节圆直径；α为接触角；ωs为轴的转动频率；n为轴的转速。

变形量λ定义为

(7)

式中：Cd为缺陷深度；b为缺陷沿外圈滚道圆弧切线方向的宽度。

开关量βj定义为

(8)

(9)

(10)

式中：φ0为初始钢球与缺陷的位置角差值；φ0e为缺陷初始位置角；Δφ为缺陷跨度角；nj为常数；re为外圈沟道半径。

将(4)～(10)式联立代入(3)式便可得到δj，根据Hertz弹性接触变形理论，在第j个钢球处接触载荷为

(11)

则在x,y向作用于外圈的总的接触载荷为

(12)

当轴承在激振力的作用下工作时，受到x，y向的合力为

(13)

式中：k为等效接触变形系数；Fr为轴承在振动机械中受到的激振力；me为轴承振动时参振质量，即外圈质量。

将(3)，(12)，(13)式代入(2)式，并联立(1)式即可得到振动机械轴承外圈单点点蚀故障的振动模型。

1.2 内圈单点点蚀

轴承内圈受力如图4所示，将轴承的振动看作是内圈相对外圈的运动。以水平向右为x轴正向，竖直向上为y轴正向。

图4 内圈有单一点蚀时轴承模型

当轴承内圈有故障点时，为方便建模，假定内圈不动，即外圈以角速度ωs沿与内圈旋转方向相反的方向旋转，则钢球公转的角速度应为ωs-ωc。与外圈建模理论同理，当外圈相对内圈在水平和竖直方向分别移动x和y时，钢球与内外圈接触总变形量δj为

δj=xcosθj+ysinθj-Gr-βjλ,

(14)

(15)

(16)

(17)

(18)

式中：φ为第1个钢球的初始位置角。

联立上述方程可得，轴承在激振力的作用下工作时，受到x，y向的合力分别为

(19)

式中：mi为轴承振动时参振质量，即内圈质量。

2 数值仿真及频谱分析

以1308调心球轴承为例，以单列为研究对象，轴承质量m=0.355 kg，钢球个数Z=15,钢球直径Dw=12.5 mm，球组节圆直径Dpw=65 mm，外圈沟道半径re=36.79 mm，内圈沟道半径ri=28.76 mm，接触角α=30°，外圈故障尺寸be×Cde为1 mm×0.2 mm，内圈故障尺寸bi×Cdi为0.7 mm×0.2 mm。计算得轴承钢球通过内、外圈的故障频率为

图5 振动机械轴承外圈单点点蚀

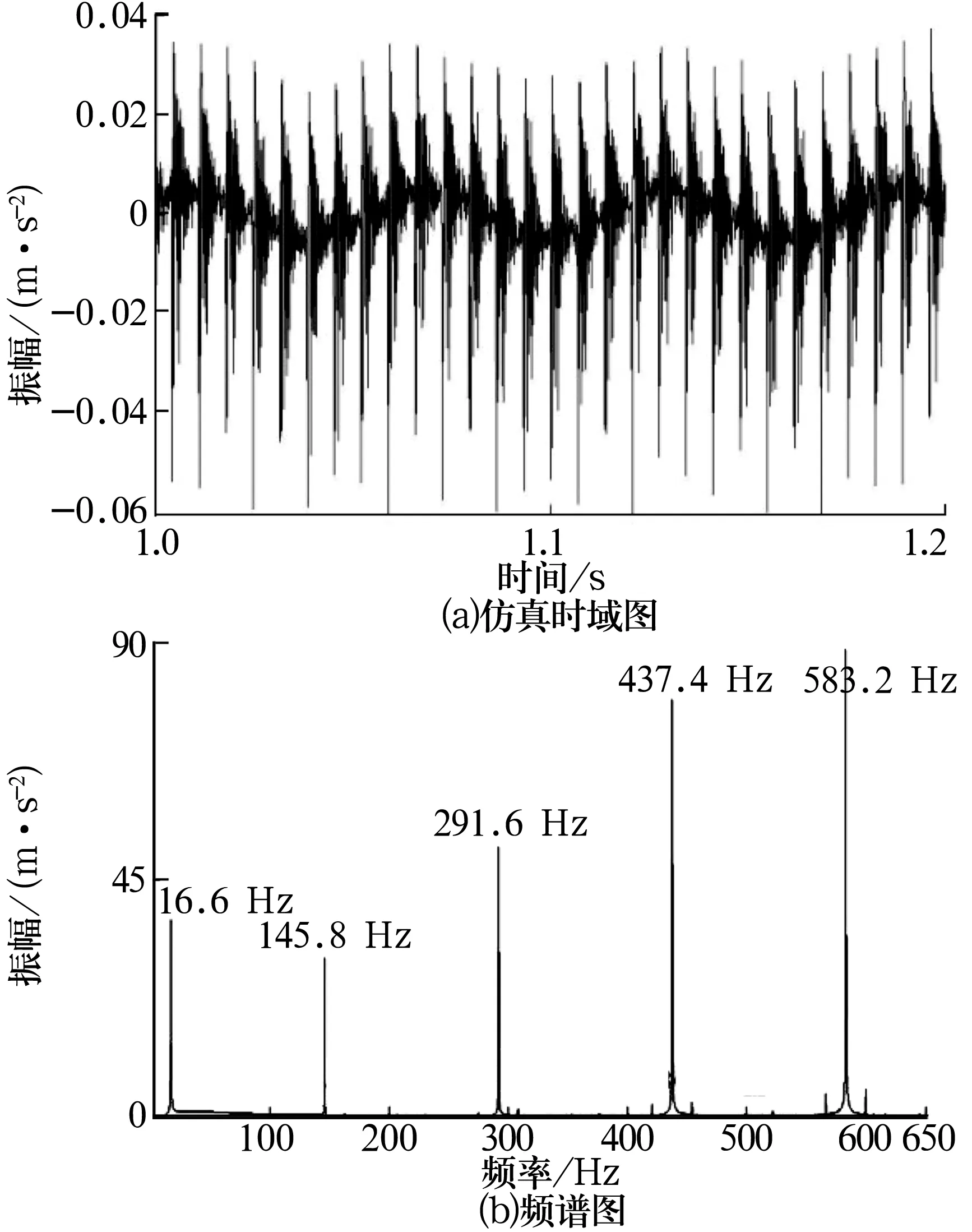
图6 振动机械轴承内圈单点点蚀

对于外圈点蚀故障，由图5可以明显看到故障特征频率及其倍频。在振动机械中，由于旋转的激振力Fr相对故障点位置不断变化，而轴承所受重力相对故障点均不变且Fr>>G,所以引起点蚀位置处接触力的幅值变化较为明显，发生调制现象，频谱中会有明显的调制频率fs=16.67 Hz及其与故障频率的叠加。

对于内圈，激振力随点蚀位置一起转动，在其故障曲线谱值中有着明显的故障特征频率fi及其倍频。由于两者相对位置不变且Fr>>G,因此只能会引起点蚀位置处接触力幅值的较小变化，即存在轻微的调制。

3 试验分析

3.1 模型验证

为验证理论模型的正确性，以振动筛为例，对1308调心球轴承内、外圈单点点蚀及正常情况进行试验，对采集数据进行包络等分析并与仿真结果进行对比，结果如图7所示。

(a)正常信号时域波形

由图可知，当轴承正常工作时，除了旋转频率fs，实测波形的频谱中不存在各种故障频率；当轴承存在单点点蚀时，实测信号频谱中存在故障频率及其倍频，并且在这些频率附近有明显的边频。考虑到误差的存在，试验结果与理论仿真结果基本一致。

3.2 对比分析

采用凯斯西储大学转子试验台轴承故障数据中心数据，轴承型号为6205，钢球个数为9个，故障尺寸为φ0.5 mm×0.25 mm,外圈试验时电动机转速为1 752 r/min，即29.2 Hz；内圈试验时电动机转速为1 750 r/min，即29.16 Hz。理论计算内圈故障特征频率为157.96 Hz，外圈故障特征频率为104.57 Hz。对试验数据取其稳定部分并进行谱分析，结果如图8所示。

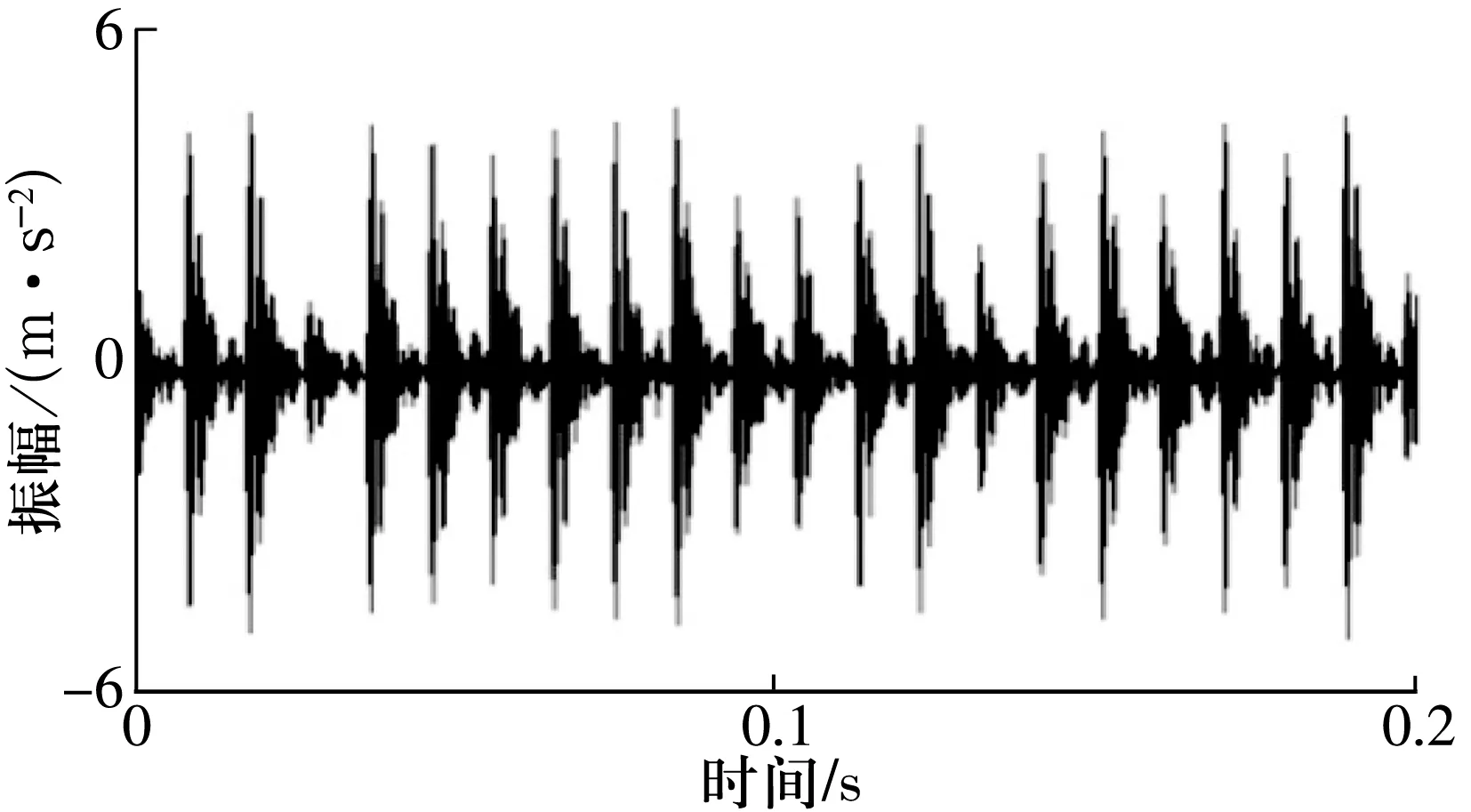
(a)外圈单点故障信号时域波形

对于外圈点蚀故障，旋转机械频谱图中有工作频率、故障特征频率及其倍频。相对于振动机械，由于外圈故障点位置不变，旋转机械中轴承主要受力来自自身及转子的重力，力相对外圈故障点的位置是不变的，因此故障信号频谱中不存在调制频率。

对于内圈点蚀故障，信号频谱图中存在工作频率及其倍频，还有内圈故障特征频率及其倍频，以及调制频率的存在。相对于振动机械，旋转机械中轴承内圈有点蚀故障时，故障点随系统一起运动，系统仅受向下的重力，因此故障点的位置相对受力方向是周期性变化的，会引起明显的调制现象。

4 结论

通过对振动机械轴承工作状态的分析，建立了振动机械内、外圈单点点蚀故障的动力学模型，应用MATLAB仿真得到故障模型的加速度曲线波形及其频谱。

利用试验分析，验证了理论建模的有效性和正确性，证实了振动机械轴承内、外圈单点点蚀故障的判据：外圈单点点蚀故障时，故障信号包络谱中存在较为明显的调制现象；内圈单点点蚀故障时，故障信号包络谱仅存在轻微的调制现象。证实了振动机械与旋转机械轴承单点点蚀故障判据是不同的，进一步完善了理论模型的研究，为深入研究多点点蚀故障提供了更多选择。