考虑径向偏移的轴向永磁轴承力学特性分析
2015-07-26倪晓艇刘飞裴旷怡孟庆涛张钢
倪晓艇,刘飞,裴旷怡,孟庆涛,张钢
(上海大学 机电工程与自动化学院,上海 200072)
永磁轴承具有无污染、低功耗的优点,符合我国节能环保、低碳经济的发展需求。然而,永磁轴承技术理论还不完善,故应用并不广泛。国内外学者对永磁轴承进行了大量研究。文献[1-2]建立了一个微型永磁轴承的解析模型,通过模拟计算和自动编程产生优化软件来优化设计微型永磁轴承中永磁环的尺寸和布局。文献[3]针对一种斥力型径向永磁轴承进行优化分析,计算出磁环的轴向总长度、气隙参数及径向刚度之间的关系,提出了提高径向刚度的优化方法。
永磁轴承磁力及刚度计算是永磁轴承研究与设计过程中的重要环节。由于目前永磁轴承的设计理论和技术尚不成熟,尚无统一的计算永磁轴承承载能力和刚度的解析数学模型[4-5]。针对永磁轴承磁力和刚度的计算方法主要为等效磁荷法、静态磁路法、矢量磁位法、虚位移法和分子电流法等。
文献[4]用分子电流法探讨了轴向永磁轴承的刚度特性,验证了分子电流法的工程应用性。但常见的两环轴向永磁轴承工作状态下两环旋转轴线发生径向偏移不可避免,偏移会对永磁轴承轴向和径向承载力产生影响。文献[6]基于分子电流法建立考虑径向偏移的轴向永磁轴承的磁力解析模型,并推导出含有四重积分的解析计算式。下文采用一种近似的蒙特卡洛法[7-8](又称M-C法)来求解方程,进一步探讨考虑径向偏移情况下的轴向永磁轴承力学特性。
1 基于分子电流法的磁力解析模型
典型径向偏移为e0的轴向永磁轴承如图1所示。假定永磁环轴向均匀充分磁化且达到饱和状态,则根据分子电流法可知:两永磁环之间的磁力可等效成下磁环内外侧表面a,b上的闭合电流环路与上磁环内外侧表面c,d上的闭合电流环路之间的磁力矢量和。两永磁环磁化方向相反,且中心轴相互平行,下磁环内外径分别为R1,R2,上磁环内外径分别为R3,R4,两磁环中心线相对位移距离为e0,下磁环厚度为L1,上磁环厚度为L2,两磁环间隙为L。表面a,b,c,d分布有环形电流,且a和d,c和b表面上的环形电流流向相同。定义下磁环表面电流强度为i1,上磁环表面电流强度为i2,l1为下磁环外表面上任一假想电流环的长度,p为电流环上的任意一点,q为上磁环外表面d上的任意一点。分子电流模型如图2所示,α,β分别为点p和点q在各自坐标系中与x(x′)轴的夹角,r为点p到点q的矢径,x为q点距上磁环下端面的距离。

图1 经典的轴向永磁轴承结构图
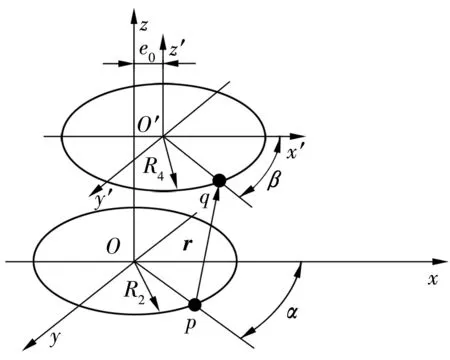
图2 分子电流模型图
磁感应强度为
(1)
式中:μ0为真空磁导率,H/m;I为感应电流,A;B为磁感应强度,T;dI为细导线电流回路I中的电流元;er为元电流单位距离。
p点的元电流在q点产生的磁感应强度为
(2)
dl1=(-R2sinαdα)i+(R2cosαdα)j,
r=(R4cosβ+e0-R2cosα)i+(R4sinβ-R2sinα)j+zk,
式中:i,j,k分别为x,y,z轴3个方向的单位矢量。
由(2)式可得下磁环外表面所有元电流的矢量和在q点产生的磁感应强度为
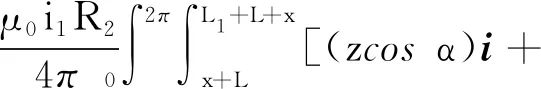
(zsinα)j+(R2-R4cos(α-β)-
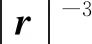
(3)
q点的元电流在磁场中的力为
dF=i2d(l2×B)dx,
(4)
dl2=(R4sinβdβ)i+(-R4cosβdβ)j,
(5)
把(3) ,(5)式代入(4)式中,并且对d面上的所有元电流进行积分便可以得到b,d面之间的力为
(Mi+Nj+Ok)dαdβdzdx,
(6)
对于永磁轴承,一般用Hc1,Hc2代替i1,i2,表示磁场强度。
力Fbd在x,y,z方向上分力分别为

(7)
(8)
(9)
同理可求a和b,c,d面间的轴向磁力分别为
(10)
(11)
(12)
对于空间中任一分子环形电流的流向考虑了逆时针旋转方向和顺时针旋转方向,故公式所列的磁力表达式均带正负号,不再考虑两侧面间的磁力为吸力或斥力的因素。
下磁环对上磁环总的轴向磁力,即该永磁轴承的轴向承载力为
Fa=Fzbd+Fzac+Fzad+Fzbc,
(13)
计算数值表示两磁环磁力大小,符号则为力的方向。符号为正,表示磁力向上为斥力;符号为负,表示磁力向下为吸力。
轴向刚度为
(14)
当轴向刚度为正时,随轴向位移增加,轴向承载力也增加,则轴向自由度稳定;反之,轴向刚度为负,轴向不稳定。
另外,可求得ac面、ad面、bc面之间的径向磁力为
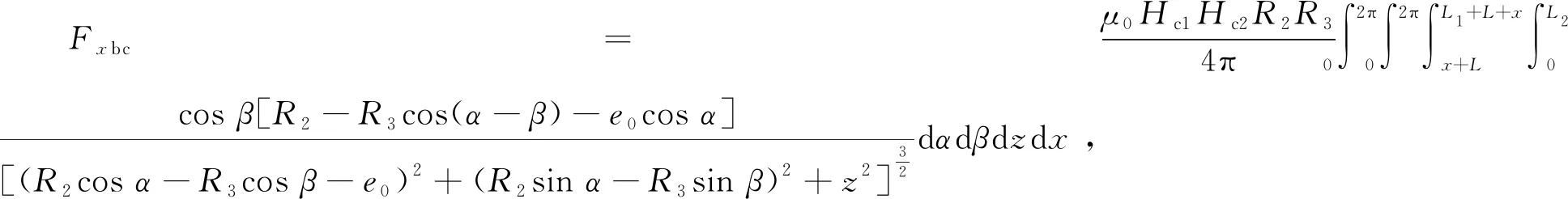
(15)
(16)
(17)
下磁环对上磁环沿x方向的径向磁力,即该永磁轴承的径向承载力为
Fr=Fxbd+Fxac+Fxad+Fxbc。
(18)
径向刚度为
(19)
当径向刚度为正时,随径向位移增加,径向承载力也增加,则径向自由度稳定;反之,径向刚度为负,径向不稳定。
2 磁力解析模型的计算步骤
2.1 积分算法的选取
根据分子电流法建立永磁轴承的磁力解析模型,推导出永磁轴承的磁力四重积分解析表达式,采用蒙特卡洛方法求解。
2.2 基于蒙特卡洛算法的编程计算
采用MATLAB进行编程计算,其中,N为采样大小;e0为初始偏移量;s为偏移步阶;a[i]为磁环间作用力的各分力值数组;被积函数f1,f2,f3,f4分别为磁力解析模型中ab面、ac面、ad面、bc面之间磁力表达式中被积函数;V1,V2,V3,V4分别表示样本中所有满足积分区域E的点求得的磁力和;Mul为积分变量上下限差值的累积值。计算步骤如图3所示。
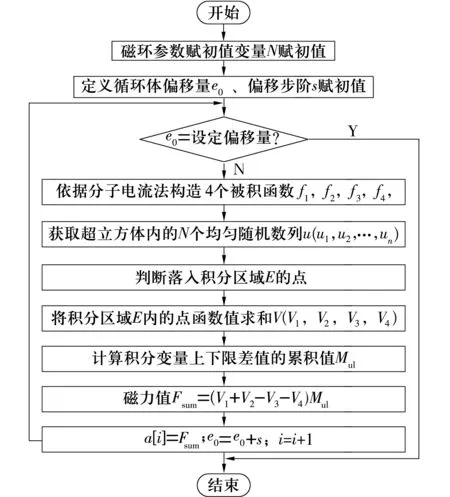
图3 蒙塔卡洛法计算磁力过程
3 实例分析
3.1 分子电流法与其他常用方法的对比
文献[9]对用于小型风力发电机中的轴向永磁轴承进行了承载试验,使用等效磁荷法、分子电流法、有限元法和试验法所得到的轴向载荷力学特性曲线如图4所示。
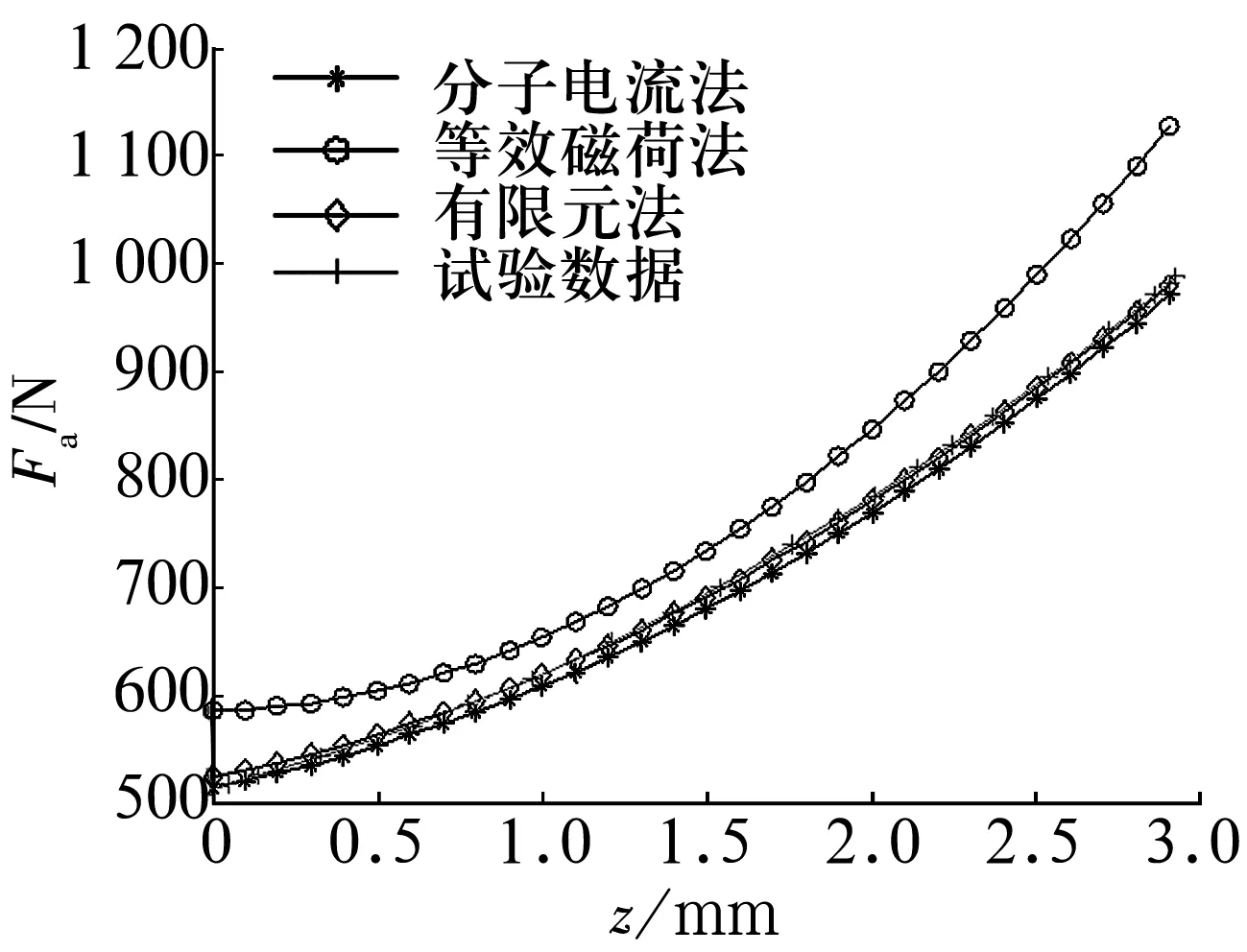
图4 力学特性曲线对比图
由图4可知,虽运用等效磁荷法建立的磁力解析模型较完善,但求解结果与试验数据相差较大,不适合精确计算,工程应用可作为初步计算;有限元法较为准确,但由于有限元需经过建模、网格划分、加载边界和载荷等步骤,在进行简单磁环的磁力分析时,比较繁琐,因此有限元法适用于磁环较多、结构比较复杂的情况;分子电流法虽然不及有限元法分析准确,但可以看出其分析结果与试验数据也非常吻合,同时采用蒙特卡洛积分算法进行编程减少了求解步骤,因此在进行简单磁环结构的磁力分析时,分子电流法显示出结果准确、计算方便的优势,可进行简单磁环结构的轴向、径向力求解。
3.2 实例分析
永磁轴承参数如下:R1=38 mm,R2=50 mm,R3=38 mm,R4=50 mm,L1=L2=12 mm,磁介质中的磁场强度Hc1=Hc2=918 266 A/M,真空磁导率μ0=4π×10-7H/m。初始轴向间隙L0=3 mm,分别讨论径向偏移e0=0,1,2,3 mm时该轴承的力学特性。
e0=0 mm时,轴向承载力及刚度随轴向位移z的变化曲线分别如图5、图6所示。随轴向位移z增加,承载力逐渐增大,且轴向承载力为正,表明轴向稳定。由图6可以看出,轴向刚度并不是一个固定值,而是随轴向位移z增加而逐渐增大,这是由于两磁环距离越近,磁感线密度增大,同时磁感线分布密度的增大幅度也变大,所以刚度增加。但是,无论轴向位移z如何变化,轴向承载力始终为正,这说明此类轴向轴承只能承受单向轴向载荷。
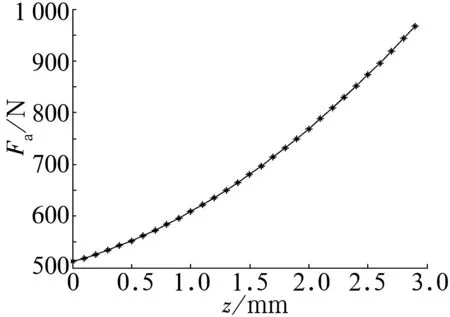
图5 轴向承载力曲线图
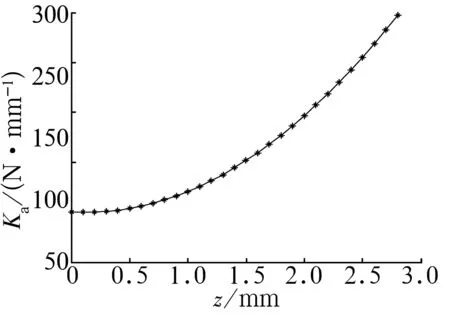
图6 轴向刚度曲线图
e0=0 mm时虚拟径向承载力及其刚度的变化曲线分别如图7、图8所示。由图7可知,虚拟径向承载力很小,且随着轴向位移z增加而逐渐减小、由正变负,这表明该永磁轴承径向不承载且不稳定。由图8可知,随着轴向位移z增加,径向刚度逐渐增加且刚度值很小、由负变正,因此其径向不稳定,故必须采用其他辅助支承使其径向稳定。
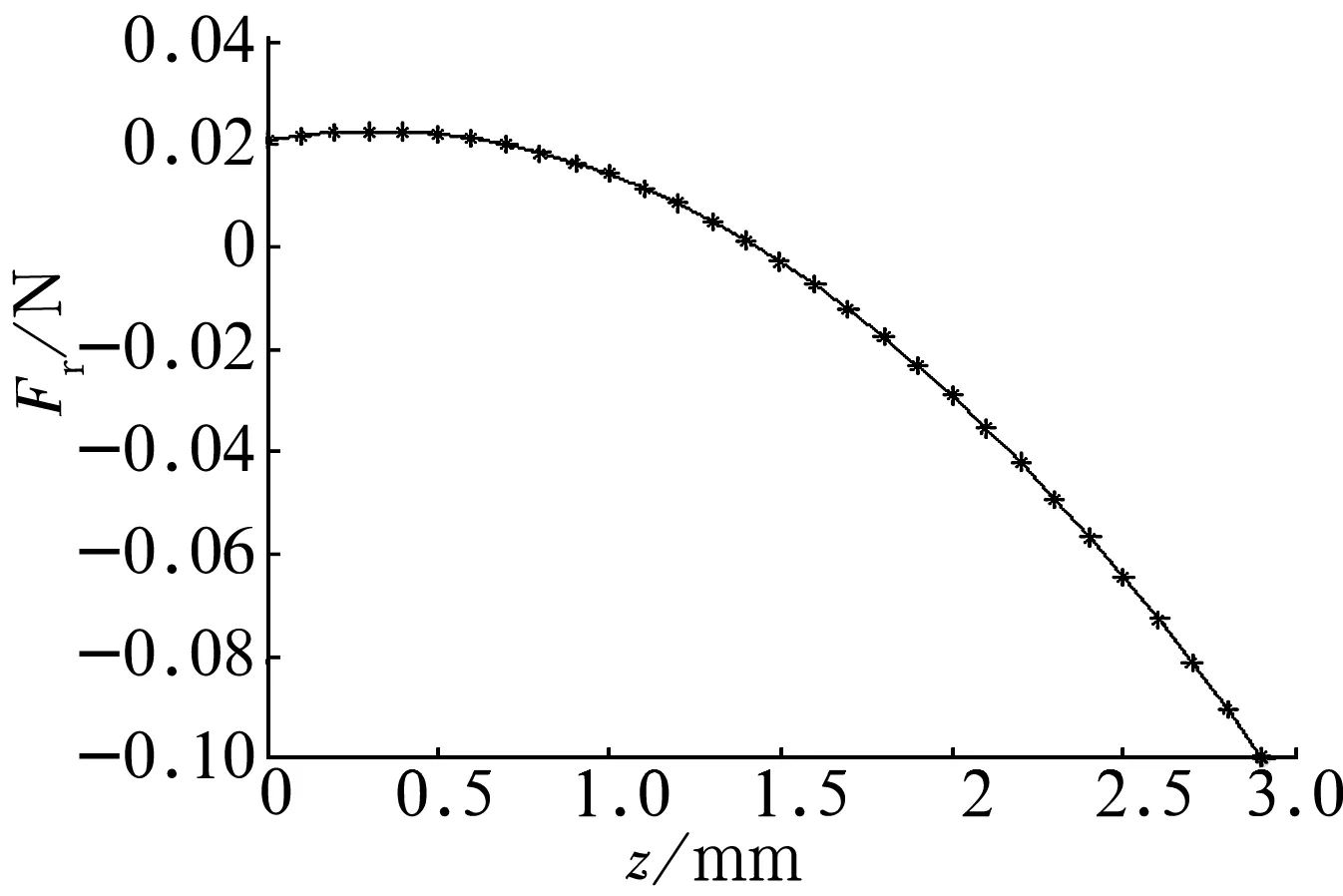
图7 虚拟径向承载力曲线图
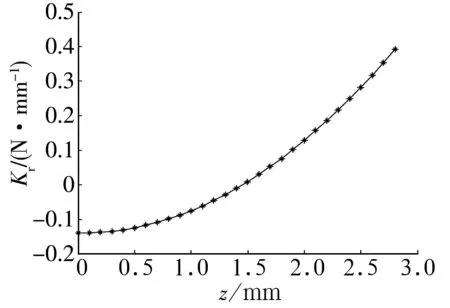
图8 虚拟径向刚度曲线图
4种不同偏移情况下轴向和虚拟径向承载特性曲线分别如图9、图10所示。由图9可知,随偏移距离变大,轴向承载力整体下降,但在偏移量固定情况下,承载力随着位移的增大而增大的趋势是不变的,因此当磁环存在偏移时,该结构磁轴承轴向承载力变化趋势保持不变,但承载能力有所降低。由图10可知,随着偏移量的增加,径向承载力均为负值,且其绝对值不断增大,表明其径向不稳定性增强;相同的偏移量下,该磁轴承的虚拟径向承载力变化更明显。
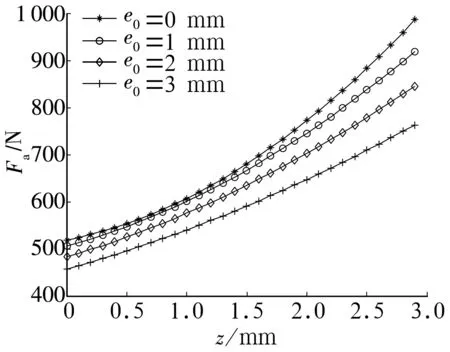
图9 不同偏移情况下轴向承载特性曲线

图10 不同偏移情况下虚拟径向承载特性曲线
4 结论
1)根据分子电流法建立了考虑径向偏移量影响的永磁轴承的磁力解析模型,推导出永磁轴承四重积分的磁力解析表达式。采用蒙特卡洛方法求解,相对省时、简单。
2) 通过实例分析表明,偏移量对轴向永磁轴承的轴向和径向承载能力会有一定影响,偏移量增加会降低轴向承载能力,增加径向承载的不稳定性。
3)径向偏移对虚拟径向承载能力影响更大,必须采用其他辅助支承使其径向稳定且能承载。
